基于潜在权重自适应分配的作战方案评估模型

李 聪， 李俊杰， 关爱杰

(中国人民解放军96901部队，北京 100000)

0 引言

作战方案是围绕特定作战目标，关于兵力部署、装备配置、作战阶段和行动协同等要素的一种形式化、规范化描述，完善可行的作战方案必须依赖于指挥人员和参谋人员对于战场态势和作战进程的精准把握、预期与设计，这直接决定了军事行动的最终结果。作战方案评估则是一种可衡量方案合理性、有效性，即方案潜在作战效能的定量化技术，它能够科学评估作战行动与打赢战争的总目标之间的系统性差距，对量化考核、方案优选、指挥决策和作战设计等现实问题具有重要的指导价值。

作战方案评估理论经过长期发展，已形成了一套庞大的方法体系[1]，具体门类上，包括传统的专家评估法、数据解析法，以及新近出现的作战仿真法、智能分析法等。然而，除了专家评估法外，其余方法在数据采集、系统建模、存储计算、适用领域等方面均有不同程度的限制，应用面较窄，专家评估法由于在原理和实现上的有效性和便捷性，目前得到了广泛应用。专家评估法中，经典的层次分析法[2]、模糊综合评价法[3]和灰色白化权聚类法[4]等仍是当前作战方案评估的主流方法，这些方法均属于多属性决策理论[5]框架，关键步骤包括：构建与量化评估指标；为评估指标赋权重；利用指标值与权重综合计算评估值。其中，为评估指标赋权重作为核心步骤，所赋权重直接反映了指标间的相对重要关系，能显著影响评估结果及结果的可信度。现阶段广泛使用的赋权法包括主观赋权法和客观赋权法[6]。

然而，这些赋权法都存在固有的局限。首先，主观赋权法主要依赖评估者的主观判断与知识经验，虽然能够很好地反映评估者的个性化决策倾向与意图偏好，但随意性较大，具有模糊性的主观经验最多可决定指标的大致重要性排序，却无法满足指标重要性的精确量化需求，且随着指标数量增多，评估者赋权成本将显著增加；其次，客观赋权法基于给定样本集中指标的内在统计特征，权重信息完全来自于样本数据的客观贡献，本质上规避了主观赋权法的随意性和模糊性，却无法反映评估者的个性化意图，导致无法融入合理的经验知识规则，而且样本集通常较为有限，指标统计特征难以避免各种抽样偏差。因此，需要一种能够恰当融合主客观两方面信息、进行主客观综合赋权的评估模型，以便在保有上述两种赋权法优点的同时，克服采用单一方法的局限，即本文的研究动机。

近年来，贝叶斯网络[7-8]这一技术在评估领域取得了广泛应用，如效能评估[9]、威胁评估[10]、风险评估[11]和毁伤评估[12]等。贝叶斯网络能够定量描述随机事件之间的因果关联关系，在处理小样本数据和不确定数据时具有显著优势。本文就是基于贝叶斯网络构建作战方案评估模型。

1 作战方案评估模型的建立

本文模型工作于有监督模式，需要一定量满足特定规则的样本集与样本标签，以驱动模型的潜在权重自适应分配过程，从而以加权和的方式推断出新方案的评估结果。

1.1 样本数据的准备

首先，根据作战目标和评估目的，通过文献综合或专家咨询等方式建立一套系统的、完备的、可量化的作战方案评估指标集合，设集合中指标数为D。其次，针对特定作战方案，利用一次或多次作战演练或作战仿真的结果数据量化指标集合，综合形成一个D维的指标样本向量x。之后，针对M(M>1)套不同的作战方案独立重复前述量化过程可获得一个M×D维的样本集矩阵X。样本集中任意指标值x*需经过规范化处理，统一为效益型指标，并映射至相同的取值区间，即∀x*∈[L,U]。最后，作战专家依据实际战果并结合个人作战知识经验，将样本集X中每个样本标注为“达标”或“未达标”，表示样本作战方案所对应的军事行动达成或未达成预定作战目标，且“达标”和“未达标”各自对应的样本数不能小于1。根据样本标签，将样本集X划分为达标样本子集XP和未达标样本子集XN。

1.2 模型的形式化描述

本文模型在概率语义层面描述了评估指标权重以及评估结果等产生过程，包含4个步骤。

1) 建立指标潜在权重的先验分布。权重向量p的先验分布指定为

p～Dirichlet(kα)

(1)

式中:Dirichlet(kα)是参数为kα的狄利克莱分布，可保证p的分量非负，且和为1，符合权重的定义；参数α为一个D维向量，每个分量代表权重的相对重要程度，由评估人员根据主观经验确定，若无额外参考信息，一般可设α的每个分量相同；实数k代表先验约束的强度因子，k值越大，权重受先验分布的影响也越大，适当调整k值可平抑小样本时抽样偏差的影响。

2) 建立达标样本子集XP和未达标样本子集XN的评估结果产生过程。对∀xp∈XP,∀xn∈XN，令

(2)

式中：yp和yn分别为样本xp和xn的评估值；符号⊙代表向量内积运算。这样，样本评估值实际由指标加权和给出。

3) 建立新样本xpre(对应新作战方案的指标向量)的评估结果产生过程，其评估值计算遵循相同的加权和过程，即

ypre=xpre⊙p

(3)

式中，ypre代表新样本xpre的评估值。新样本一般也通过作战演练或作战仿真的方式获取。

4) 建立样本特征优化过程，需要基于XP和XN两类评估结果数据，建立类间距特征优化过程和类内聚特征优化过程。设XP和XN中样本数分别为P和N，定义类间距特征Ssep和类内聚特征Ccoh为

Ssep=median({ypi|i=1,…,P})-
median({ynj|j=1,…,N})

(4)

Ccoh=max(mad({ypi|i=1,…,P}),
mad({ynj|j=1,…,N}))

(5)

式中：median为中位数函数；mad为中位数绝对偏差函数，定义为

mad({z})=median({|z-median({z})|})。

(6)

类间距特征衡量两类样本子集中心位置的距离，类内聚特征衡量两类样本的集中程度。而median和mad作为样本中心位置和集中度的鲁棒统计量，可以起到抑制样本异常点的作用。

建立样本特征优化过程的目的在于给出潜在权重应满足的约束条件，因为对于加权和方法，一旦给定方案样本，则其评估结果由权重唯一决定，而样本标签其实隐含了权重信息，最优的权重应该使两类样本最大程度分离，且样本内最大程度集中。基于这种思想，样本特征优化过程描述为

(7)

式中:Laplace为拉普拉斯分布，即双指数分布;O1和O2分别是以类间距特征Ssep和类内聚特征Ccoh为位置参数、以δ1和δ2为尺度参数的两个拉普拉斯分布的抽样值，分别代表Ssep和Ccoh的优化目标。通过设置合理的O1和O2值，可同时使类间距特征Ssep最大化、类内聚特征Ccoh最小化。一般地，可设置O1=U-L,O2=0，这样，从最大似然的观点来看，类间距将向最大值U-L逼近，同时，类内聚将向最小值0逼近，导致达标样本子集XP和未达标样本子集XN分别向高评估值和低评估值处聚拢，从而使两类样本尽量分离且样本内尽量集中，这是通过权重p的自适应分配过程实现的。

图1为本文模型的贝叶斯网络形式，圆形节点代表随机变量，节点间有向边代表变量间的概率依赖关系，模型参数也通过有向边与随机变量相连，方框表示网络结构的复制。

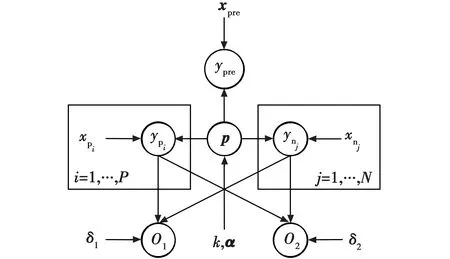
图1 模型的贝叶斯网络形式Fig.1 Bayesian network form of the model

1.3 模型推断

模型推断的目的是解算新样本评估值ypre的后验分布，即p(ypre|XP,XN,O1,O2)，这需要将样本X、样本标签和新样本xpre，以及必要的模型参数与随机变量O1和O2的观测值代入作战方案评估模型，启动对模型的推断过程。不过，由于随机变量ypre的后验分布不存在闭式解，所以采取随机抽样的方式，通过足量的样本来逼近真实的后验分布。随着抽样过程趋近收敛，潜在权重也将根据模型的输入信息自适应收敛至恰当的后验概率分布，基于此，得到新样本评估结果在区间[L,U]上的数值分布，此分布的期望值就表征新方案评估结果，而分布的标准差揭示评估结果的不确定性，即结果置信度的高低，标准差越大，代表评估结果越分散，结果置信度越低。单方案评估时，期望值越高、标准差越小，方案效能越高；多方案优选时，在期望结果类似的情况下，优选标准差最小的方案。

2 实验与分析

2.1 模型运行设置

本文实验以红蓝对抗作战方案评估为例，简要起见，从作战力量、作战保障、指挥控制和作战效果等方面梳理出图2所示的指标集合，共8项，即D=8。之后，通过调整力量编成、指挥协同、打击目标、行动流程和保障方式等因素，拟制7套不同的作战方案，将这些方案作为某作战仿真系统的想定输入，从仿真结果中采集数据并量化指标集合，形成一个7×8维的样本集矩阵X，包括表1中方案1～7的所有指标数据，且新方案的指标数据也通过仿真获得。X中任意指标值均经过规范化处理，统一为效益型指标，且映射至相同的取值区间[0,100]，即L=0,U=100。同时，表1中也包含了样本标注结果，根据样本标签，达标样本子集XP包括方案1～3的指标数据，未达标样本子集XN包括方案4～7的指标数据。

后续实验中，将表1的方案1～7样本和新方案样本代入模型，并设置模型参数k=2，α=[1,1,1,1,1,1,1,1]，δ1=1，δ2=2，以及变量观测值O1=U-L=100，O2=0。本文使用Stan概率建模工具实现模型的概率语义，借助其内置的NUTS(no-U-turn sampler)方法[13]实现对模型的抽样过程。

图2 评估指标体系Fig.2 Evaluation index system for operation scheme

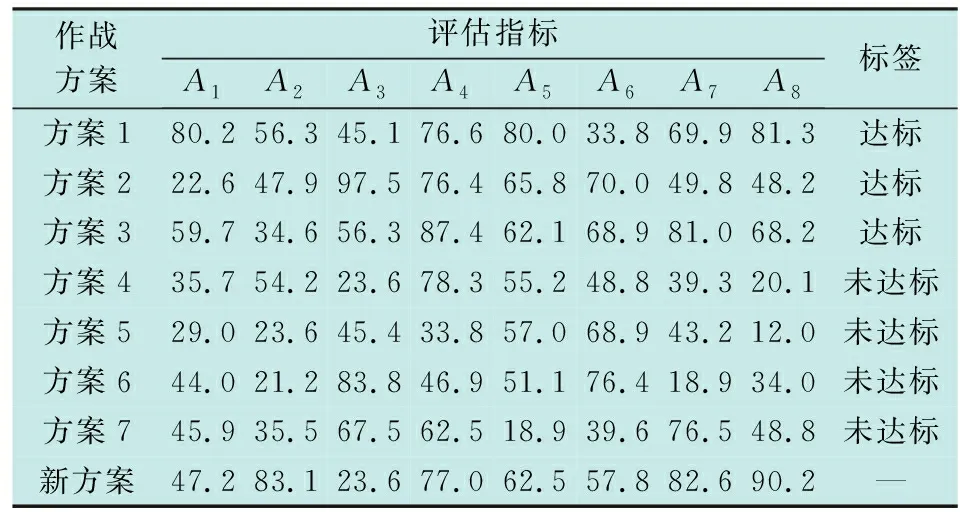
表 1 样本数据Table 1 The sample data

2.2 结果分析

新作战方案评估值ypre的后验分布样本在区间[0,100]上的概率分布情况见图3。通过进一步计算得出，方案评估值期望为77.2，处于中等偏上区间，表明方案总体上具备可行性，且标准差为3.2，值较小，从而分布较为集中，表示方案评估结果的置信度较高，可确切地作为军事行动的决策依据。同时，对权重向量p也进行后验抽样，将每个分量的后验分布样本，即每项评估指标的权重分布，以盒图形式绘制为图4。从图中易见，指标A1～A6的权重较小，而指标A7和A8的权重明显偏高，表明方案评估结果很大程度上由指标A7和A8决定，其余指标的作用较弱。从表1中也可以发现，达标样本的这两项指标总体上优于未达标样本，而其他指标值在两类样本中分布相对混杂，无明显规律，这从侧面揭示出本文模型潜在权重自适应分配过程的有效性与合理性。

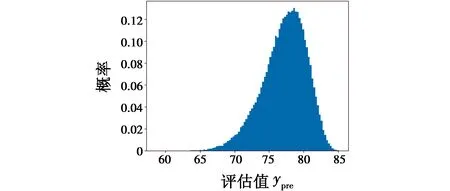
图3 新方案评估值的分布Fig.3 Distribution of evaluation value of the new scheme

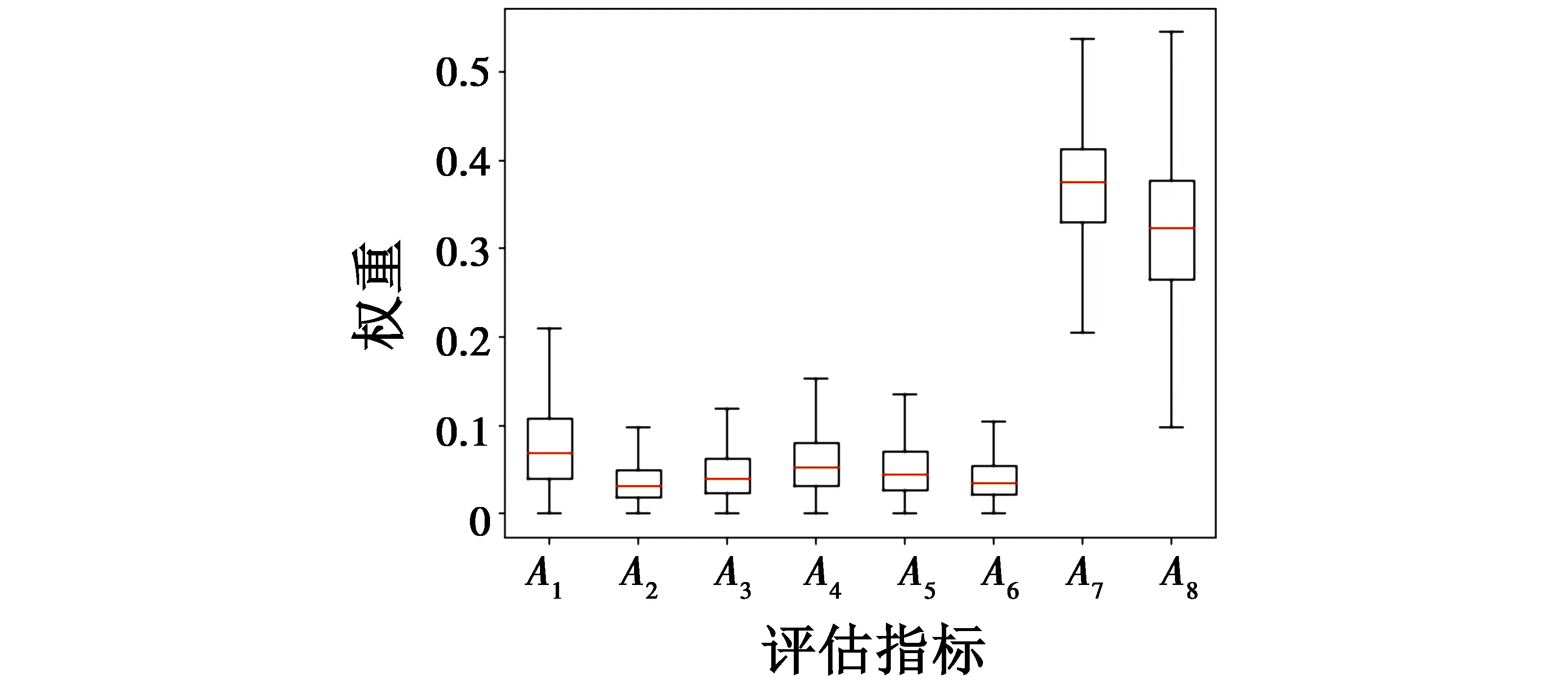
图4 指标权重的分布Fig.4 Distribution of the index weights

3 结束语

本文提出了一种基于潜在权重自适应分配的作战方案评估模型，其潜在权重自适应分配过程根源于主观的样本标签和客观的样本指标，本质是一种基于主客观综合赋权的评估方法，可克服单一采用主观或客观赋权法的固有局限。同时，给出的方案评估结果不是固定值，而是一个随机变量，这样，除了期望值可直接作为评估结果外，其分布标准差还能揭示评估结果的分散程度，间接表明结果的置信度。特别地，本文模型基于贝叶斯网络构建，故具有贝叶斯方法在小样本上的使用优势，即在给定恰当的先验信息后，用少量样本就可有效训练模型，显著降低了数据采集成本，符合实际运用需求。模型为作战方案评估提供了新的思路与方法，未来工作将致力于研究模型的变分推断方法。