基于线路数据信息的列车定位方法研究

2022-02-22宋海锋张敏杰曾小清应沛然冯栋梁

同济大学学报（自然科学版） 2022年1期

宋海锋，张敏杰，曾小清，应沛然，何乔，冯栋梁

（1.北京交通大学电子信息工程学院，北京 100044；2.同济大学道路与交通工程教育部重点实验室，上海 201804；3.贝尔福-蒙贝利亚技术大学信息学院,贝尔福 90000，法国；4.上海市市政工程建设发展有限公司，上海 200025）

列车运行和控制系统是整个高铁系统的核心，列车运行数据对于分析列车运行状态具有重要意义。新建线路在进行实际客运运营之前必须经过多次测试，以获得列车在线路运行中的相关数据，如运行时分、速度、位置等信息。获取的数据用于分析列车运行状态，发现设计过程中的不合理情况确保列车运行安全，诸多信息中获取列车运行的实时速度与位置是至关重要的。

列车定位方法有绝对定位和相对定位两种。近年来，许多学者对基于全球定位系统（global navigation satellite system，GNSS）的列车定位方法进行了研究［1-2］。由于列车运行环境的复杂性，单纯GNSS在某些特定场景下无法提供可靠的位置数据。应答器为列车提供了单点定位的绝对位置，并根据速度传感器、惯性传感器（inertial measurement unit，IMU）扽推算出列车的相对位置。但是当列车运行在有遮挡、无卫星信号的环境中，GNSS不可以提供可靠的位置信息；IMU测量的误差会随时间累加，长时间的单纯的使用IMU测量列车速度与位置会有很大的误差［3］。由于速度传感器的累计误差和答应器的铺放密度等，依靠单一的传感器难以实现精准、连续的列车定位。多传感器融合定位方法成为主要的研究方向［4-6］。

论文主要考虑在失去卫星信号情况下来实现列车的精确定位，在当前的大多数研究中常考虑使用列车的速度传感器以及应答器的信息来确定列车的速度与位置信息，但是这两种信息的获取都有一定的限制。通常无法直接获取速度传感器的信息，而且相邻应答器之间还存在一定的距离，尤其对于既有的普速线路、重载专用线路等没有应答器的线路，在考虑列车出现故障的情况下，无法根据应答器获得列车的位置信息。论文考虑到这些背景条件下，利用既有车载设备采集列车的平顺度信息作为参考模板，为解决两次成功匹配定位期间的连续定位问题，提高数据估计精度介入惯性测量单元。因此，基于动态时间规整（dynamic time warping，DTW）算法的不规则匹配可以为提供列车一个精确的绝对定位信息且没有累积误差，论文引入DTW算法的自适应分块匹配，为IMU分时提供校准数据，最终实现列车的实时精准定位。

1 数据预处理

论文采用惯导芯片采集列车的俯仰角-时间信息作为测试模板数据与高精度设备采集的同一条线路的俯仰角-时间的参考模板数据进行匹配，在数据进行匹配之前需要对数据进行预处理。由于传感器本身以及测量过程都存在噪声影响会导致测量结果有一定的偏差，并且测量过程中列车的震动以及运行环境的影响也会对采集的数据有一定的影响，因此，需要对采集的数据先进行数据滤波。常用的滤波方法有卡尔曼滤波（Kalman filtering，KF），扩展卡尔曼滤波（extended Kalman filter，EKF）和无迹卡尔曼滤波（unscented Kalman filter，UKF）等［7］。本文采用卡尔曼滤波的算法对采集的列车不平顺度信息进行滤波处理。具体的滤波方式如下：

通过陀螺仪可以得到列车的俯仰角信息以及角速度信息，根据俯仰角以及陀螺仪角速度的关系建立模型。

系统状态方程：

系统观测方程：

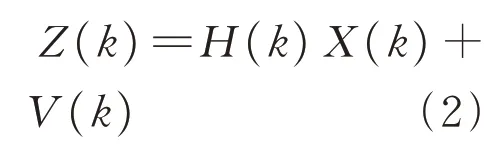
式（1）—（2）中：X(k)为k时刻的目标状态估计值，X(k)的状态向量是俯仰角的角度θ和俯仰角的偏差σ，即X(k)=[θσ]T；u(k)为k时刻的陀螺仪的角速度；Z(k)为观测k时刻的跟踪目标的量测值；A为状态转移矩阵，B为输入转换为状态的矩阵；H为观测矩阵；W(K)为过程噪声矩阵；V(k)为系统观测噪声；Q为过程噪声协方差矩阵，R为观测噪声协方差矩阵（理想情况下过程噪声协方差与观测噪声协方差均被视为均值为0的高斯白噪声）。

由运动模型可知：

式中：Δt为采样时间间隔。卡尔曼滤波包括两个阶段：预测阶段和更新阶段，在预测阶段，卡尔曼滤波器通过使用上一状态的估计，对当前状态进行估计。在更新阶段，滤波器通过预测出的状态值，对系统进行更新［8］。

式中：K(k)为卡尔曼滤波增益。

2 基于DTW的不规则匹配

通过使用高精度测量工具，例如激光雷达［9］，或实际铁路现场建设过程中的线路数据信息，可以获取列车线路的不平顺数据。根据测量的线路平顺度与距离关系作为基本指标，可以用来计算列车位置估计，如图1所示。

图1 俯仰角序列与距离的数据图Fig.1 Data map for pitch angel sequence versus distance

需要注意的是，即使使用高精度传感器来获取原始值，列车在同一条线路上运行，由于列车运行在不同环境与不同场景下运行，也会存在误差。

时间序列是一种非常常见的数据存在方式，在大多数数据挖掘工作中，计算时间序列之间的相似度是一个经常遇到的任务。但在现实中，用于相似度计算的时间序列往往在时间轴上有大致的相似性，但具体的对应关系是不可知的。

如图2所示，采集列车运行数据的时候是按时间顺序进行收集的，时间序列是一种非常常见的数据存在方式，尤其对于列车运行过程列车的不平顺度信息对应与列车运行时分。在大多数数据挖掘工作中，计算时间序列之间的相似度是一个经常遇到的任务。但在现实中，用于相似度计算的时间序列往往在时间轴上有大致的相似性，但具体的对应关系是未知的。如果采用传统的欧几里德距离进行计算，则不会考虑时间上的动态变化，这显然会造成很大的误差［10］。

图2 俯仰角序列与时间图Fig.2 Pitch angel sequence versus time

基于上述问题的考虑，单纯的根据时间进行单点对单点的匹配是满足不了实际情况，使用DTW（动态时间规整）算法可以满足单点对多点或者多点对单点匹配。DTW算法是一种动态规划算法，计算两个时间序列的相似度，尤其是不同长度的序列［11-12］，可以对序列的延展以及压缩具有较好的适应性。主要用于时间序列数据，如识别、数据挖掘、信息检索等。

假设两个时间序列Q与C，他们的长度分别为n与m，两个序列如等式（10）所示：

当m=n时，两个时间序列长度相等，不需要对两个数据进行缩放直接对齐匹配。在m≠n，两个时间序列长度不相等的情况下，就需要采取动态规划（DP）的方法［13］。为了对齐序列Q与C，就需要构造一个矩阵网格。如图3所示，矩阵网格中元素w(i，j)表示qi和cj两个点的欧式距离d(qi，cj)=(qi-cj)2。DP算法可以归结为寻找一条通过此网格中若干格点的路径，寻求两个序列的最优匹配结果就是寻找该网格图中一条最优路径。

图3 矩阵网格图Fig.3 Matrix grid

为了对齐两个时间序列，寻求最优匹配路径，需要对寻求路径施加一定的限制条件。条件如下：

（1）边界条件：路径必须从网格的左上角w(1，1)开始，从网格的右下角结束w(m，n)结束；

（2）连续性：w(i，j)的下一个连接点必须是w(i-1，j)，w(i，j-1)和w(i-1，j-1)三个点中一个，不能跳过这三个点直接与其他点连接；

（3）单调性：w(i，j)必须根据时间序列单调前进。

结合上述条件，可以得到规整代价最小的路径如下：

其中，分母中的K主要是用来对不同的长度的规整路径做补偿。从w(1，1)点开始对这两个序列Q与C开始匹配，每到一个点之前的所有的点计算的距离都累加，最终到达终点w(m，n)［14-15］可以得到一个总的累计距离，这就是序列Q与C的相似度。累计距离公式如下所示：

D（Q，C）是从w(1，1)点开始到w(i，j)的路径累计距离。

对序列Q与C的相似度进行分析，设定相似度阈值，通过与设置阈值比较来判定这两个序列是否匹配。

在对采集的数据进行滤波处理后，对采集的参考模板数据以及测试模板数据用DTW算法进行匹配，最终可以根据DTW计算得出最优匹配结果，并且根据参考数据的俯仰角-距离关系可以得到列车的位置-时间关系，列车车速-时间关系从而得到匹配的测试模板俯仰角所对应的列车速度和公里标信息。基于DTW方法，运行距离与时间、距离与时间的关系分别如图4、图5所示。

图4 车辆行驶距离与时间图Fig.4 Vehicle running distance versus time

图5 车速与时间Fig.5 Vehicle speed versus time

3 IMU/DWT融合

列车运行的环境复杂多变，在很多情况下列车运行在无卫星信号，如何获取列车的运行的位置与速度是至关重要的。在国内外研究中，常常使用惯性导航系统对列车进行推算定位。

惯性导航系统最主要的部分是惯性测量单元（IMU），主要用来检测和测量加速度与旋转运动的传感器，其原理是采用惯性定律实现的。最基础的惯性传感器包括加速度计和角速度计（陀螺仪），他们是惯性系统的核心部件。论文采用的IMU是由三个加速度计和角速度计（陀螺仪）构成，加速度计检测物体在载体坐标系统独立三轴的加速度信号，而陀螺仪检测载体相对于导航坐标系的角速度信号，测量物体在三维空间中的角速度和加速度，并以此解算出物体的姿态。惯性导航系统通过安装在运载体的IMU中的陀螺仪与加速度计测量数据，可以确定运载体在惯性参考坐标系中的运动，同时也能够计算出运载体在惯性参考坐标系中的位置［16］。

IMU由于制作工艺的原因，惯性传感器测量的数据通常都会有一定误差。主要有加速度计与陀螺仪的漂移误差，就是在载体静止状态下传感器有非零的输出。要想得到位移数据，需要对加速度计的输出进行两次积分。在两次积分后，即使很小的偏移误差会被放大，随着时间推进，位移误差会不断积累，最终导致没法再跟踪物体的位置。因此单纯的使用惯性导航系统不可以对列车进行定位。因此惯性导航常常与全球定位系统结合使用，通过全球定位系统在有卫星情况下接收的数据对下一次惯性导航系统进行一次数据校准。那如何在无卫星信号的情况怎么对惯性导航系统进行数据校准对提高定位精度是至关重要的。论文采用分块DTW匹配的方法对列车无卫星信号的情况下对列车实时运行数据进行周期校准。

分块DTW算法就是对DTW算法的参考模板进行分块处理，如图6所示对参考模板的数据按照数据或者数据时间进行分块，设定一个阈值，对实时采集的测试数据按照更小块的数据与参考模板分块后的数据进行DTW匹配。

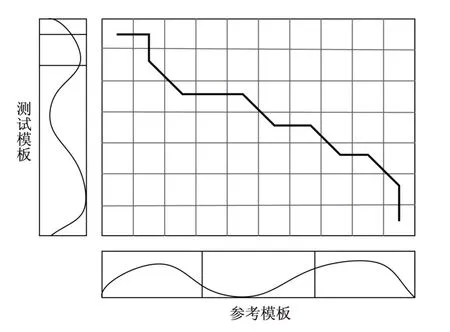
图6 分块匹配网格示意图Fig.6 Schematic diagram of block matching grid

分块匹配的过程可以对实时运行的列车提供当前的列车的线路的大概定位，匹配的结果可为实时列车提供一个准确的位置，这可以作为一个IMU的校准数据。通过调节分块的大小与设置阈值可提高定位精度。论文通过DTW不规则匹配获取列车运行数据与IMU采集列车实时运行数据融合可实现

从轨迹匹配图的结果可以看出动态时间归整算法在参考模板与测试模板匹配上有很好的结果。通过最优匹配路径可以得到参考模板与测试模板的对应关系，根据不规则的数字地图可以得到离线状态下列车运行的速度，位置信息。

在很多情况下需要对列车的实时运行信息进行分析。这种情况下怎么实时获取列车变得至关重要。对于需要实时获取列车运行数据信息的情况，论文采用INS（惯性导航系统）与DTW算法相结合实现列车无信号情况下的实时定位。其中需要对列车更加精准的实时定位。

4 案例分析

利用动态时间归整算法对列车同一条线路的平顺度-时间信息进行匹配。用高精度的设备采集线路的平顺度信息作为线路参考模板，再次测量该线路平顺度信息作为测试模板。把参考模板与测试模板作为两个序列（Q和C），为了对齐这两个序列，需要构造一个n×m的矩阵网格，矩阵元素(i，j)表示qi和cj两个点的距离d(qi，cj)（也就是序列Q的每一个点和C的每一个点之间的相似度，距离越小则相似度越高，d(qi，cj)越小相识度越高）。

在进行匹配之前，需要对列车的平顺度信息进行标准化处理后再进行数据分析。数据标准化处理的主要原因是不同评价指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。论文采用最大-最小标准化对列车平顺度信息进行归一化处理。将一个原始值X通过最大-最小标准化映射到区间［0，1］的值Xnorm，如式（13）所示：

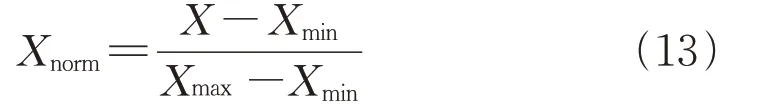
式中：Xmin与Xmax为原始值中最小与最大值；Xnorm为原始值X进行归一化处理后的结果。每一个矩阵元素(i，j)表示点qi和cj的对齐。采用DP（动态规划）算法来寻找一条通过此网格中若干格点的路径，路径通过的格点即为两个序列进行计算的对齐的点。根据欧式距离公式和限制约束条件，可以得到一个最优的规整路径，如图7、图8所示。

图7 最优匹配路径图Fig.7 Optimal integration path

图8 路径匹配结果Fig.8 Matching result

DTW算法的参考模板进行分块处理（对参考模板进行均匀二分，四分与八分等）。根据设置最优匹配路线d(m，n)的阀值，对列车实时数据作为测试模板与当前的分块的参考模板进行匹配，最终得到的最优匹配路径可以得到目前列车处于的线路段信息，根据最优匹配结果得到目前列车的位置信息。图9—12是对参考模板进行二分与四分的最优路径图以及匹配结果图。根据分块的多少调节阀值，可以得到最优的匹配结果。模板分块划分也有自己的局限，不能划分的过多，过多可能匹配结果出错。

图9 二均分最优匹配路径Fig.9 Even division of the optimal matching path

根据分块匹配的结果，得到列车位置。通过参考模板的俯仰角-公里标与俯仰角-时间关系可以得到测试列车的时间-速度与时间-公里标关系。根据匹配结果得到的列车运行数据作为IMU的校准数据实现更加精准的列车定位，具体过程本文不做赘述。

5 结论

利用惯性导航芯片采集到列车线路的平顺度信息，基于DTW的不规则匹配可以为列车提供为一个粗略的实时定位且没有累积误差。通过参考模板建立的不规则地图以及参考模板的时间-速度与时间-公里标关系，可以为离线的测试列车提供位置与速度信息。为了实现列车的实时定位，使DTW的不规则匹配与IMU结合，结合DTW无累计误差的优点为IMU提供误差修正使列车运行数据有更好的估计精度。