核零空间方法在乳腺癌异常检测中的应用

韩 笑，毕 波,，唐锦萍，曹 莉

(1.东北石油大学 数学与统计学院，黑龙江 大庆 163318；2.海南医学院公共卫生学院，海南 海口 571101;3.黑龙江大学 数据科学与技术学院，黑龙江 哈尔滨 150080)

0 引 言

当今时代，乳腺癌已成为女性最为常见的恶性肿瘤，其发病率在全球范围内均持续增长，每年的确诊人数约高达28万，具有较高的死亡率，并且越来越倾向于年轻化。临床研究表明，乳腺癌的演变过程大致可以概括为五个步骤，由一开始乳腺的良性病变，之后乳腺良性增生，乳腺不典型增生，再到后来的乳腺原位癌，到最后的浸润性的乳腺癌，但并不是所有的患者都一定会按照这样的规律逐渐演变，有时在临床当中也可能会发现跳跃式的演变。因此，要想预防乳腺癌或得到早期的治疗，就必须及早地进行检测，发现异常，采取相应的应对措施。

核零空间算法作为一种单分类算法，经常用来进行异常检测。起初它是源于线性判别分析(LDA)的，利用最大化Fisher准则的思想，将所有的样本点通过某种线性变换(即FST变换)，达到最小化类内散度，最大化类间散度的目的。之后将类内距离变为0，提出了零空间变换(即NFST变换)。但是，这两种变换都是仅仅考虑了数据的线性特征，而数据往往还存在许多非线性特征，因此提出了该变换的核化方法，即KNFST变换。首先利用核函数将数据进行非线性映射变换到高维空间，然后再利用NFST变换思想，提取使得类内散度为0，且类间散度最大的特征方向，即提取零投影方向。乳腺癌样本往往具有多个显式的线性特征，但也具有很多观测不到的隐式的非线性特征，因此为了更好地提取样本的非线性特征，提高乳腺癌样本数据的异常识别率，利用核零空间算法对乳腺癌数据进行异常检测。

该文总结了零空间方法以及核零空间算法的计算步骤，有效提取了样本数据的非线性特征。将核零空间算法用于UCI数据库中的乳腺癌数据集进行仿真实验，通过对比不同核函数以及不同异常阈值下的异常识别率，充分证明了将核零空间算法用于乳腺癌异常检测的有效性。

1 核零空间方法

若

X

={

x

,

x

,…,

x

1,

x

,

x

,…,

x

2,…,

x

1,

x

2,…,

x

}为一个含有

N

个样本的数据集，其中

X

∈

R

,设

X

={

x

,

x

,…,

x

1}，

X

={

x

,

x

,…,

x

2}，…,

X

={

x

1,

x

2,…,

x

}为

C

个不同的类，其中第

i

类的类内均值为：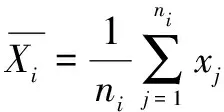

(1)

总均值为：

(2)

1.1 Fisher准则

假设

φ

为LDA算法的投影矩阵，则Fisher准则公式为：

(3)

考虑到基于最小化类内散度，最大化类间散度的特点，需要计算类内方差矩阵与类间方差矩阵，分别将类内散度矩阵与类间散度矩阵定义如下：

(4)

1.2 NFST变换

由于很多时候，样本数往往远远小于数据的特征维数，这时会导致奇异。为了解决这个问题，将类内方差规定为0，因此提出了零空间线性变换，即(NFST变换)。则令：=0

(6)

>0

(7)

为了同时满足上述两个条件，在计算时引入了总散度矩阵,令：=+

(8)

零投影方向计算步骤如下：

第三步：得到总的零投影矩阵=。

1.3 KNFST变换

通过零空间变换，得到的也仅仅是使得分类结果最优的线性特征组成的投影矩阵，但是很多数据集往往不仅具有显式的线性特征，而且具有隐式的非线性特征，因此，就提出了核零空间变换(KNFST变换)。这时就需要先利用核函数将低维数据映射到高维非线性特征空间，然后再进行零投影矩阵的计算。设经过非线性映射后的特征空间为

F

,非线性映射后的样本为

φ

(

X

),则此时有：第

i

类的类内均值为：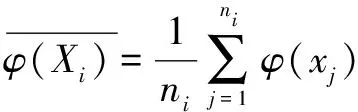

(9)

总均值为：

(10)

(11)

(12)

(13)

由于为了提取数据的非线性特征，将其利用核函数映射到了高维空间，因此，在计算时需要对映射后的数据进行零方向投影，现在需要计算核矩阵的类内方差、类间方差。其中核矩阵中的每一个元素都可以表示为样本间的内积形式：

K

=(

φ

(

x

),

φ

(

x

))=<

φ

(

x

),

φ

(

x

)>

(14)

其中，

k

=1,2,…,

c

,

l

=1,2,…,

n

。

核类内方差矩阵为：

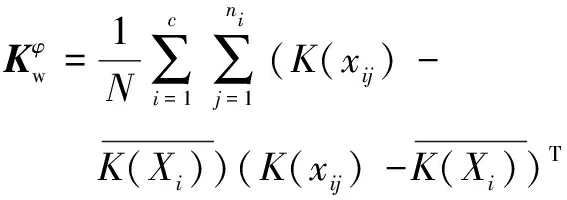
(15)

核类间方差矩阵为：

(16)

核总方差矩阵为：

(17)

零投影方向具体计算步骤如下：

第一步：非线性空间投影，

X

∈

R

→

φ

(

X

)∈

F

。

第四步：得到总的零投影矩阵=。

在得到零投影矩阵以后，首先将训练集的核投影矩阵按照零投影矩阵的方向，将整个训练集投影为一个单点，之后将测试集中的每一个样本先按照非线性映射方向，得到测试集在非线性映射方向的核投影矩阵，然后再将其按照零投影矩阵的方向投影到零空间上的单个点，最后计算零空间上每个测试点到正常点样本的距离，并且通过判断该距离与事先设定的异常阈值的大小，来判断测试样本是否为异常样本。

2 实验应用分析

由于医疗行业的特殊性，时时刻刻都在产生海量的医疗数据，数据挖掘和机器学习技术为这些海量医疗数据的分析和应用提供了新的思路和手段。通过读取乳房X光造影的测量指标，用机器学习算法来检测乳腺癌，是目前人工智能和医学领域交叉的研究热点。

该文选取核零空间算法对乳腺细胞的各项测量数据进行异常检测，但是乳腺癌样本数据的特征维数很多，因此如何有效地进行非线性映射是取得满意结果的关键。运用核零空间算法进行乳腺癌异常检测主要依赖于核函数的选取以及核函数参数和异常阈值的设置。下面分别对乳腺癌数据在不同核函数、不同核参数和不同异常阈值下的F1-score做了对比，并且得出了结论。

2.1 数据准备

选取UCI数据库中的breast-Cancer数据集作为实验数据集，它一共包含699个样本数据，其中良性样本数据有458个，恶性样本数据有241个，其中每个样本都含有9个特征，分别为：Clump Thickness，Uniformity of Cell Size，Uniformity of Cell Shape，Marginal Adhesion，Single Epithelial Cell Size，Bare Nuclei，Bland Chromatin，Normal Nucleoli，Mitoses。除此之外，还含有16处缺失值。

(1)数据缺失值处理：利用缺失值所在列的平均值填充缺失值。

(2)数据归一化处理：数据特征不同，对应的值可能存在的差异特别大，因此为了减小这种影响，对数据先进行归一化处理，将每个值都设定在[0,1]范围内。这里分别对每个样本的每个特征都做归一化处理，即：

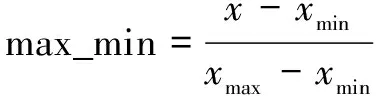
(18)

其中，

x

表示每一列的最小值，

x

表示每一列的最大值。

(3)数据集划分：对归一化后的数据进行测试集与训练集的划分，将所有正常样本的70%作为训练集，剩下的30%作为测试集的一部分，然后再将所有的异常样本放入测试集中，共同组成完整的测试集。

2.2 核函数选取

分别利用多项式核函数与高斯核函数建立核矩阵。

多项式核函数为：

K

(

x

,

y

)=(1+

x.y

)

(19)

高斯核函数为：

K

(

x

,

y

)=e-(-)

(20)

利用训练集建立核矩阵，计算零投影方向，然后将测试集按照该方向投影在零空间上，通过计算测试集的F1-score来验证模型的有效性。

2.3 实验及结果分析

首先利用核零空间算法对乳腺癌训练集建立模型，然后再利用乳腺癌样本数据测试集对该模型进行测试，得到不同条件下的识别率。

分别取多项式核函数

d

=2,

d

=3,

d

=4,

d

=5，以及高斯核函数的ROC曲线，如图1～图5所示。

图1 d=2的多项式函数的ROC曲线

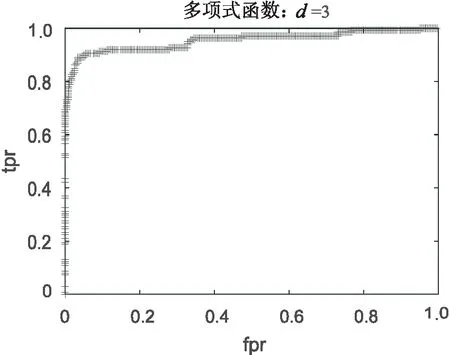
图2 d=3的多项式函数的ROC曲线

图3 d=4的多项式函数的ROC曲线

图4 d=5的多项式函数的ROC曲线

图5 γ=1的高斯核函数的ROC曲线

通过观察图像，利用多项式核作为核函数时，在

d

=2时，模型表现最差，之后随着参数

d

的增加，在

d

=3时，表现最好，随后，

d

=4,

d

=5时，模型表现逐渐变差。这说明利用多项式作为核函数时，选取

d

=3为最佳参数。但是，相比于多项式作为核函数，发现使用

γ

=1的高斯核作为核函数时，模型的表现要比任何参数下的多项式函数的表现都好，当然高斯核函数也可通过调节参数得到不同的结果，但这里仅讨论

γ

=1时的高斯核函数。因此，利用核零空间算法对乳腺癌数据进行检测时，利用高斯核函数要优于多项式核函数。

下面是具体地使用不同核函数时，取所有样本点到正常点的测试样本的平均值(Mean)作为异常阈值与取使得F1-score不等于1的最大值对应的测试点的距离作为异常阈值(Best)的F1-score结果对比。

表1 不同核函数下取Mean与Best作为异常 阈值的F1-score结果

通过观察图表发现，纵向来看，无论利用什么核函数，当选取测试集到正常点的平均距离(Mean)作为异常阈值进行判断时的识别率都比选取Best作为异常阈值的F1-score分数低。横向来看，仅看多项式函数时，最佳F1-score为取参数

d

=3时，获得最高的F1-score分数91.45%，随后，随着参数的增加，F1-score分数逐渐减少，但是，若取

γ

=1的高斯核作为核函数，则模型的F1-score分数要远远超过任何参数下的多项式核函数的模型F1-score分数，达到了96.27%。这表明使用

γ

=1的高斯核作为核函数时的模型的性能比任何参数下的多项式核函数的模型的性能都好。

综上所述，在利用核零空间算法进行异常检测时，选取一个合适的核函数以及定义一个最佳的异常判别阈值，对模型的结果有很大的影响。在对乳腺癌数据集进行异常检测时，选取高斯核函数进行非线性映射无疑是要优于多项式核函数的。

3 结束语

该文基于最大化Fisher原则，利用核零空间算法在处理高维数据及有效提取数据非线性特征上的优势，将其运用于UCI数据集的乳腺癌数据集上，通过MATLAB仿真实验发现，使用

γ

=1的高斯核作为核函数时的模型的F1-score分数比任何参数下的多项式核函数的模型的F1-score分数都高，并且不同异常阈值下的F1-score分数也不同，充分证明了运用核零空间算法进行乳腺癌异常检测的有效性。未来如何通过建立更加有效的核函数，选取更加合适的异常阈值从而实现更高的识别率，加快大数据集的运行速度仍然是一个值得深入研究的问题。