基于灰狼算法的民航维修人为差错评价模型
2022-02-22麻鹰,王瑞
麻 鹰,王 瑞
(上海大学 通信与信息工程学院,上海 200444)
0 引 言
人为差错是在民航安全中被广泛提及的一个词,它是指人未能按既定计划完成规定任务,从而造成设备、财产损失的行为。
文中设计了一种基于深度学习算法的人为差错评价模型,有助于加强民航企业内部对维修人员的人为差错的管控,降低维修中人为差错的发生率,提高安全生产质量。同时弥补了现阶段民航企业内部对维修人员个体人为差错管控上存在的实时性、预测性、针对性的缺陷。
该系统深度学习算法的核心是通过分析人为差错的诱因,构建基于径向基神经网络评价模型;首次提出惯性自适应灰狼算法训练径向基神经网络的权值和阈值,从而使系统具有良好的实用性、准确性。
1 模型构建
1.1 输入层/输出层设计
评价系统的影响因子(输入层)通过研究人为差错的经典文献:SHEL模型、REASON模型、墨菲定理、HFACS系统,结合企业业务特点(东航虹桥维修基地为例),以《航空人员的维修差错管理》为基础,提出了各层面:自身层面(M1-M4)、环境层面(N1-N4)、组织层面(X1-X4)、管理层面(Y1-Y6)共计18个影响人为差错的因子,如表1所示。
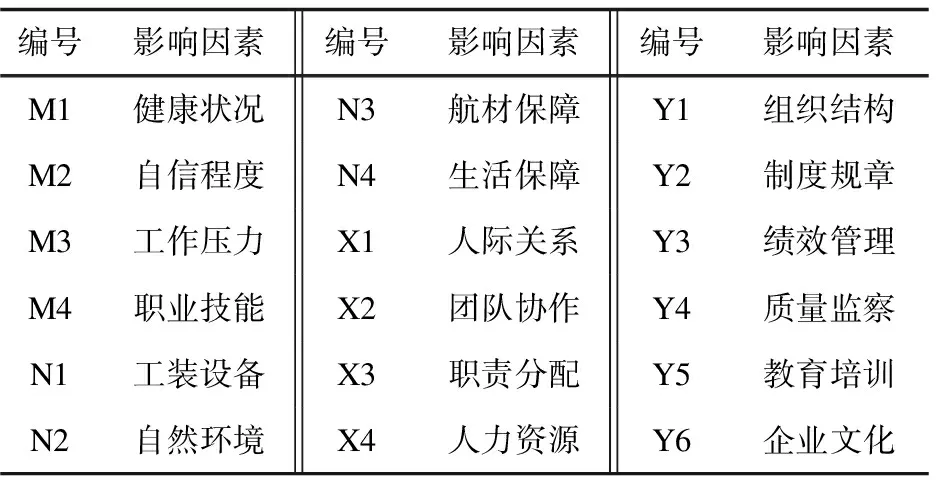
表1 影响人为差错的因子
系统的评价等级(输出层)则主要参考东航《机务维修人员安全积分的管理办法》:安全积分以一个自然年为周期,共计10分。发生一般维修差错/严重维修差错/维修事故症候,根据情节的严重程度,扣除安全积分1分~3分/3分~7分/7分~10分;走访东航虹桥维修基地质量部门4名专家,以及大量在岗维修人员,最终确定见表2:将现有安全积分3分(含)以下定义为不安全,即容易发生人为差错;将现有安全积分7分(含)以下定义为一般,即可能发生人为差错;将现有安全积分7分以上定义为安全,即不容易发生人为差错。

表2 评价等级与输出层期望值
1.2 算法设计
(1)径向基神经网络。
径向基函数(radial basis function,RFB)神经网络是由J.Moody和C.Darken在80年代末提出的,它是具有单隐层的三层前馈网络。由于它模拟了人脑中局部调整、相互覆盖接收域的神经网络结构,有很强的非线性拟合能力,可映射任意复杂的非线性关系,而且学习规则简单,便于计算机实现。具有很强的鲁棒性、记忆能力、非线性映射能力以及强大的自学习能力。因此,RBF神经网络是一种局部逼近网络,能够以任意精度逼近任意连续函数,特别适合于解决分类问题。
(2)灰狼算法。
灰狼算法(grey wolf optimization,GWO)是一种基于动物行为学的智能算法。其主要通过模仿狼群的社会关系,以及它们的狩猎、捕猎行为,构建数学模型。狼群共分为4个阶层,每个阶层都有严格的阶级分工:α
狼是整个狼群的首领,是最高阶层的狼,对狼群有着绝对的领导能力,狼群中任何狼都必须听命于α
狼;β
狼是仅次于α
狼的第二阶层狼,它只听命于α
狼,并协助领导其余狼;δ
狼再次之,服从α
狼、β
狼的领导,且只可以领导普通的ω
狼。围猎行为:
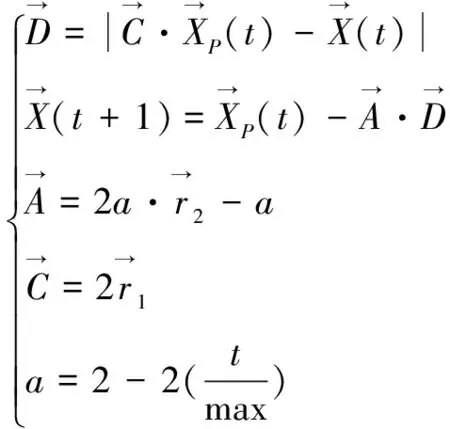
(1)
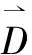
狩猎行为:
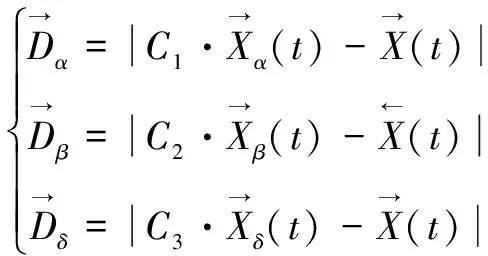
(2)
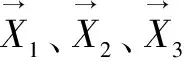
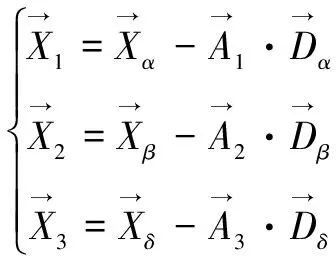
(3)
式(3)分别定义了ω
狼群中个体朝向α
、β
、δ
前进的步长和方向,式(4)定义了ω
狼的最终位置。
(4)
(3)粒子群算法(PSO)。
粒子群算法(particle swarm optimization,PSO)是受到鸟群在觅食中迁徙、聚集行为的启发。初始状态下,PSO是一群随机的粒子,粒子在迭代过程中受到个体极值和全局极值的影响,使粒子向空间内最优解趋近并降落。
核心公式如下:
v
=ω
·v
+c
·r
(pbest-x
)+c
·r
(gbest-x
),x
=x
+v
(5)
其中,i
=1,2,…,N
,N
是粒子总数;v
是粒子速度,r
、r
是[0,1]的随机数;c
、c
学习率为一个常数;ω
是惯性因子,是个非负数。1.3 算法优化
(1)社会信息共享机制。
受粒子群算法的启发,根据ω
狼迭代时的更新位置受到全局最优解(α
、β
、δ
狼)的影响,建立整个狼群的信息共享交流机制。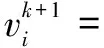
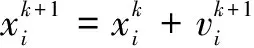
(6)
(2)自适应惯性因子策略。
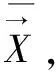
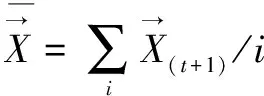

(7)
式中,ω
为ω
的初始值,ω
为ω
的终值,t
为最大迭代数。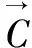
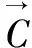
综上所述,IAHGWO算法训练RBF神经网络的步骤如图1所示。
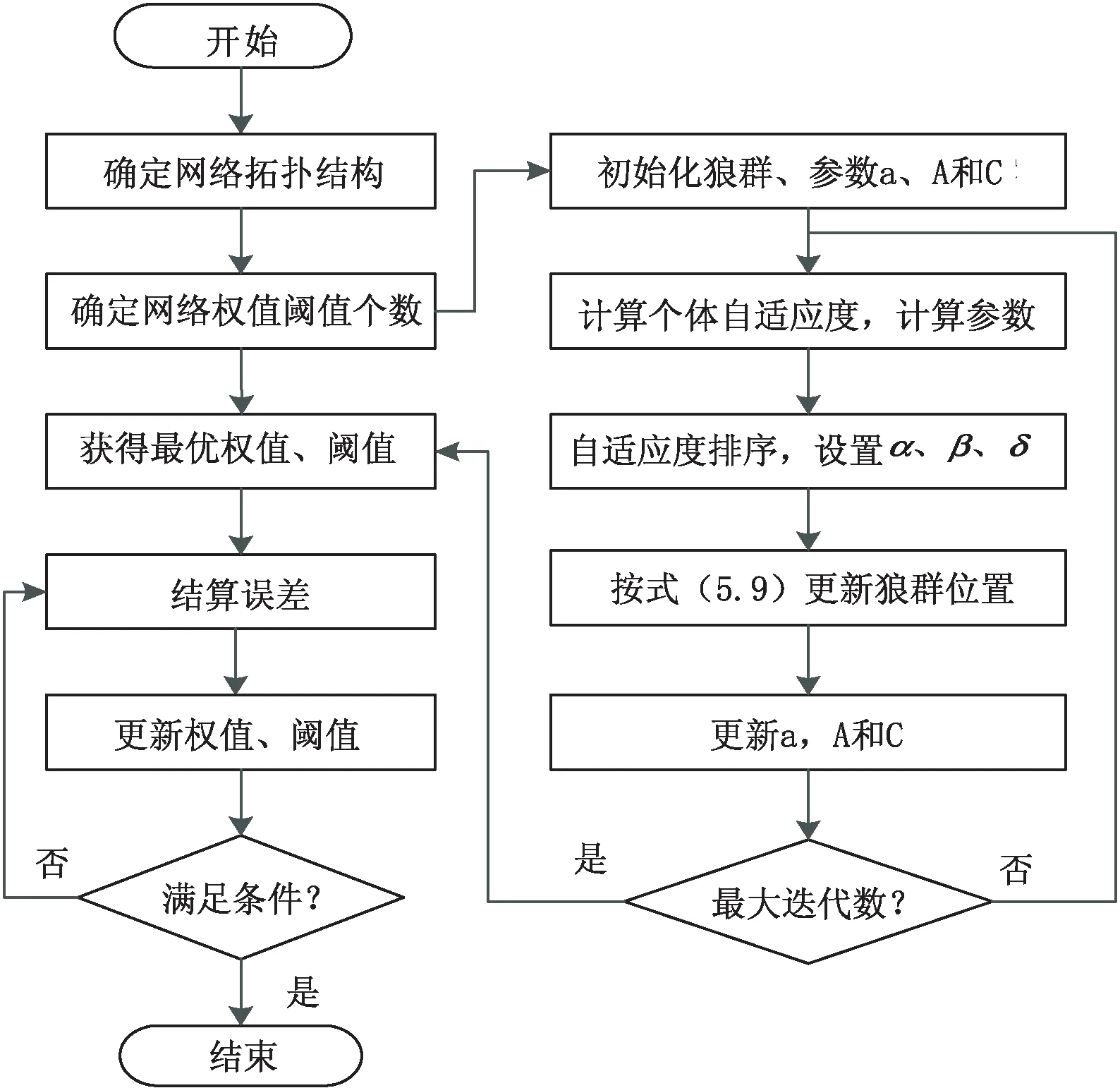
图1 混合灰狼算法训练RBF神经网络流程
1.4 对比仿真
通过MATLAB2018a进行仿真对比实验,在灰狼算法原文采用的23种基准函数表中分类选取其中具有代表性的基准函数表(见表3)作对比。设置狼群总数30;迭代次数500,取30次仿真的平均值,图2展示了寻优迭代效率。
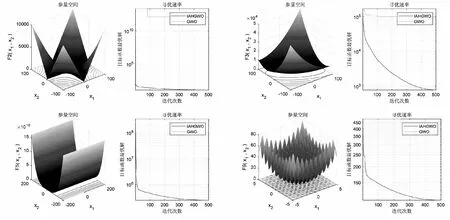
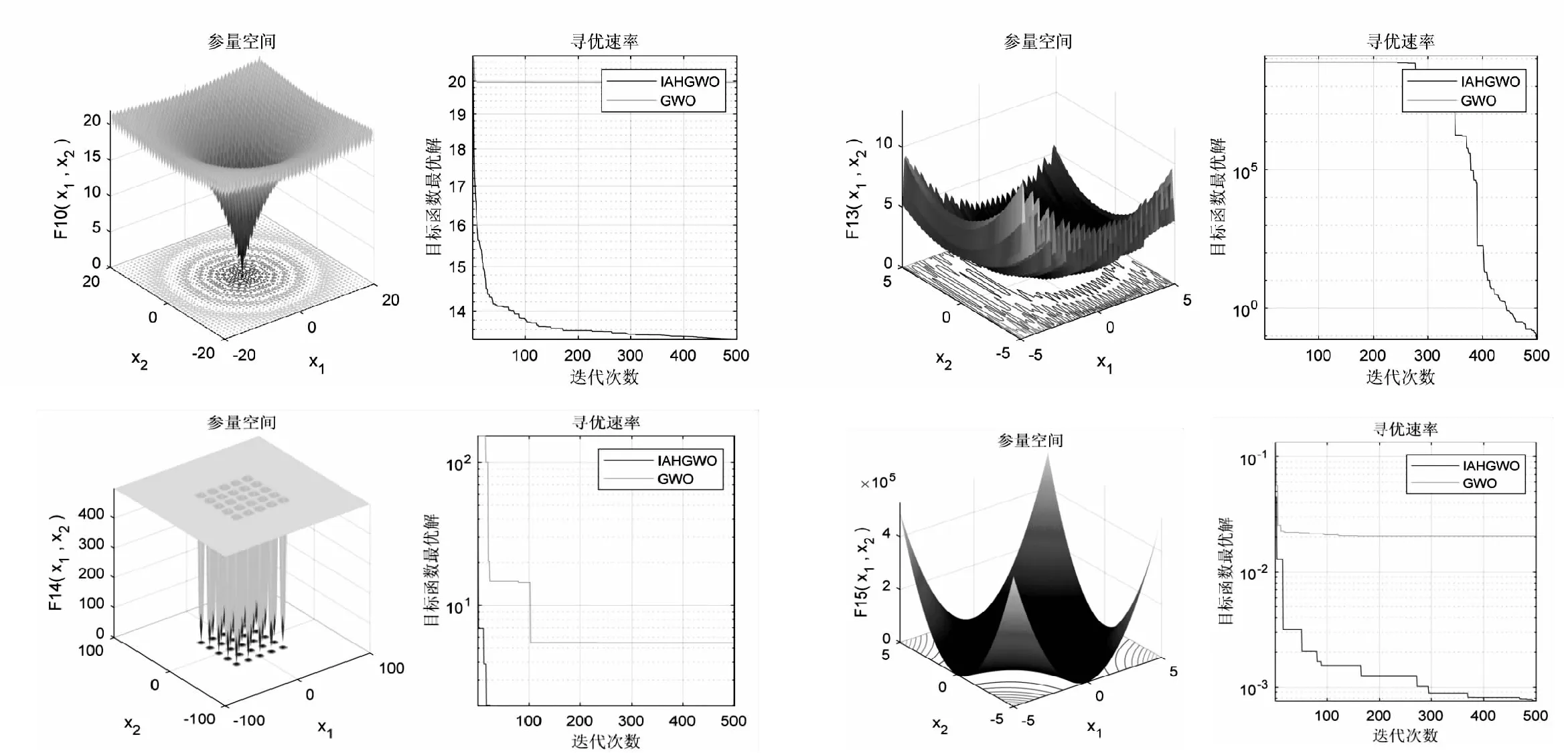
图2 IAHGWO与标准GWO性能对比
通过比较可以明显看出,文中提出的惯性自适应混合灰狼算法(IAHGWO)在性能上明显优于标准灰狼算法,将惯性自适应混合灰狼算法的适应度函数设为:
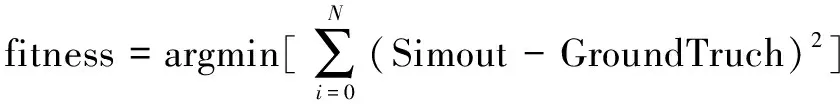
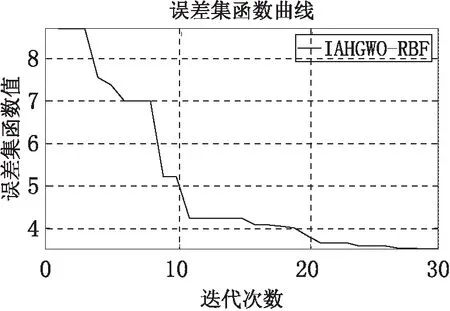
图3 混合灰狼算法训练RBF神经网络误差曲线
优化后的RBF神经网络误差值如图3所示,呈持续下降的趋势。说明IAHGWO对RBF神经网络起到了优化作用,使RBF神经网络的正确率从87.65%提升到了95.88%。
2 数据采集分析
以东航虹桥维修基地为例,在其内发放问卷200份,回收173份,其中有效问卷157份,有效问卷回收率为78%。被试者的工作司龄都在2~20年间,从事一线维修工作。对采集的数据运用SPSS22进行信度和效度分析,结果如表3、表4所示,表明上述问卷采集的数据可以被采纳。

表3 基准函数参数

表4 信度与效度校验参数
3 模型应用
使用MATLAB2018a将采集的数据代入标准RBF神经网络进行训练,结果见图4。可以看出,RBF神经网络的误差在第251步完成收敛。说明所构建的RBF神经网络模型与民航维修中的人为差错,建立了良好的非线性关系。表5为东航虹桥维修基地两名一线维修人员的原始数据,通过IAHGWO-RBF模型计算,得到与期望值几乎近似的数值,且与两人实际相符,可以说该模型具有相当强的实用性。
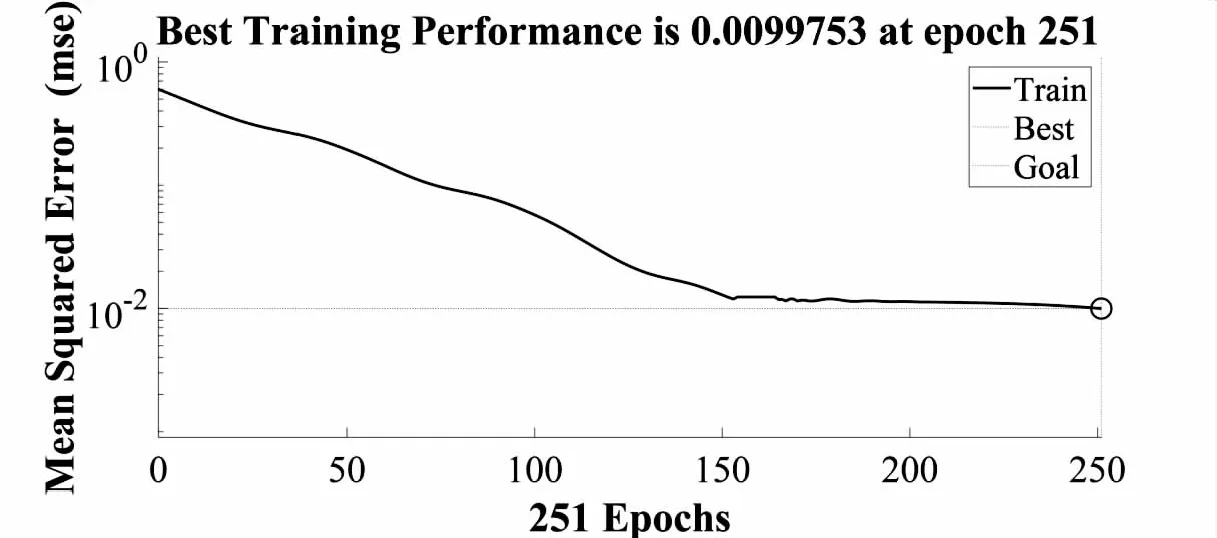
图4 RBF神经网络收敛曲线
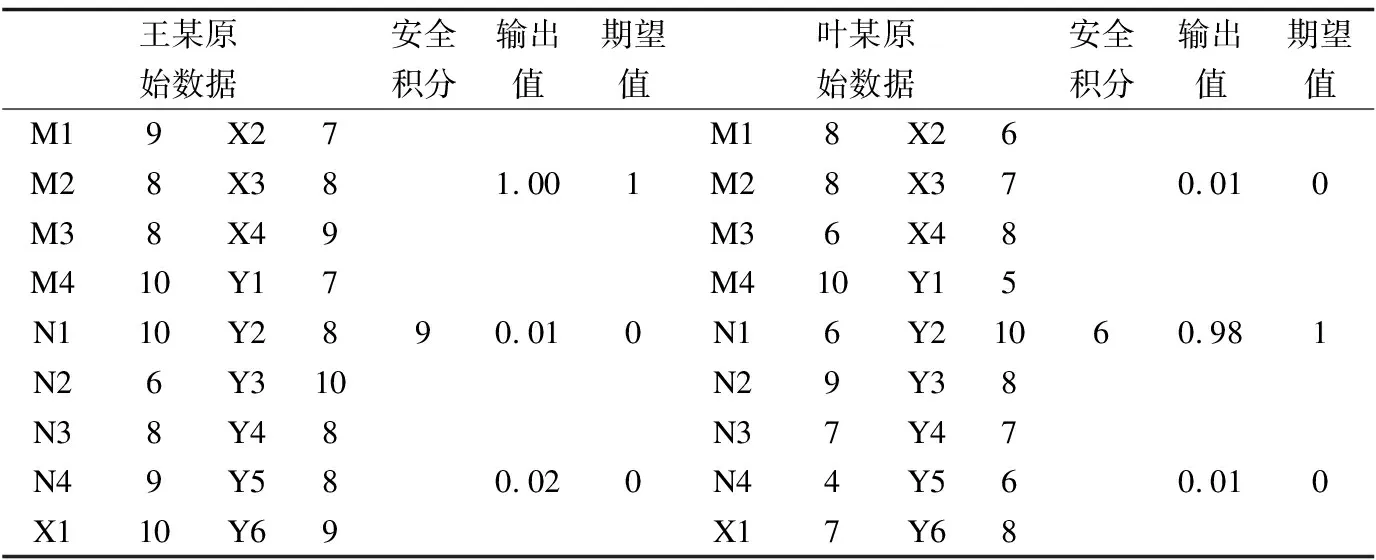
表5 原始数据计算结果
4 结束语
提出一种惯性自适应混合灰狼算法,通过与标准灰狼算法做仿真比较,证明了该算法的优越性。
通过惯性自适应混合灰狼算法训练后RBF神经网络,误差显著下降,准确率从87.65%提升到了95.88%以东航虹桥维修基地为例,验证了构建的民航维修人为差错评价模型具有良好的实用性和准确性。为后期的推广提供了实践基础。
