铰链式下垂前缘机构设计与动力学仿真研究

冯蕴雯，蔡昂，何智宇，周颖，薛小锋

（1.西北工业大学 航空学院，西安 710072）

（2.上海飞机设计研究院飞机结构强度工程技术所，上海 201210）

0 引 言

机翼增升装置是现代大型民用飞机起降过程中的关键机构，增升装置设计也是民用飞机研制中主要任务之一。经过国内外的长期研究，增升装置中以前缘缝翼和后缘襟翼为代表的设计技术与方法等较为完善，但是目前已经运用的增升装置结构复杂，会造成飞机使用过程中的可靠性降低、维护检查困难等一系列问题。现如今大型民用飞机使用需求的不断变化以及飞机设计技术的不断发展进步，绿色航空、安全航空的发展理念已经成为当前民用飞机的设计指导思想，特别是伴随着飞机噪声要求的提高，增升装置设计的指导思想和目标转变为在满足气动要求及噪声要求的前提下尽可能地做到简单、可靠，例如先进商用飞机A380 和A350XWB 在机翼上便采用了铰链下垂前缘的增升装置，说明铰链式的下垂前缘相比于运用较多的传统滑轨式前缘缝翼具有更高的可靠性。这种增升装置是一种简单的前缘绕铰链轴向下旋转一定角度的结构，与目前使用最多的前缘缝翼相比，这种结构具有减小阻力、降低噪声、提高升阻比和可靠性等优点。

下垂前缘式的增升装置机构结构型式简单、噪声小、失效概率低，已经成为当前国际先进民用飞机增升装置的主要研究方向。由于前缘下垂构型与主翼之间不存在缝道和凹腔，这种增升装置可以大幅减小气动噪声，且铰链机构结构型式简单、重量轻，降低了制造维修成本，较好地满足了飞机总体技术要求。

国外下垂前缘的增升装置机构设计方法很完善，例如，J.Adam 等在欧洲NACRE 项目资助下设计了一种先进的下垂前缘增升装置。但国内对下垂前缘机构的设计方法研究还很少，大多是对下垂前缘气动特性的研究，例如刘沛清等近年来对下垂前缘气动特性进行研究。对于增升机构的设计方法，张兴国从RSSR 空间刚体引导机构出发，探讨了主襟翼运动机构的设计方法；舒培等创建了增升装置机构设计子平台的方法来设计后缘襟翼机构；张中波利用图解法和模拟仿真的方法设计了一套以后缘后退开缝襟翼为基础的驱动机构；赵立杰等以NACA2418 标准翼型前缘为对象，提出一种基于离散材料优化（DMO）法的复合材料机翼前缘柔性机构拓扑优化设计方法。

综上所述，国内对于铰链式下垂前缘机构的设计方法鲜有研究。本文从下垂前缘的机构型式、运动要求出发，利用构造下垂前缘机构的线架模型和模拟仿真的方式，提出基于四连杆形式的下垂前缘机构设计方法，得到下垂前缘的机构型式；用动力学中刚柔耦合动力学仿真方法代替传统刚体动力学方法，考虑前缘翼面的变形，分析机构运动特性以及载荷状况，用于验证该设计方法的可行性。

1 下垂前缘机构设计方法

1.1 设计要求与思路

本文提出的下垂前缘机构确定为铰链式下垂前缘，机构的运动轨迹初步定义为绕固定转轴进行旋转的曲柄摇臂机构，机构的运动平面与转轴垂直，转轴位置视机翼后掠角而定，因此机构运动平面以及下垂前缘的运动方向近似与机翼前缘垂直，针对这种下垂前缘机构运动形式，设计一种可以使前缘翼面能够定轴旋转下偏的下垂前缘运动机构，具体设计要求如下：

（1）下垂前缘机构简单、占用空间小、重量较轻；

（2）下垂前缘机构在运动过程中，翼面能够在驱动的作用下运动连续平稳；

（3）下垂前缘机构能够均匀承受气动载荷；

（4）避免下垂前缘机构在运动过程中发生碰撞或产生干涉；

（5）下垂前缘的驱动机构采用多余度设计，且在运动过程中相互不影响。

得到的下垂前缘机构的设计方案流程如图1所示。首先分析设计输入并以此为基础构建机构的线架模型，对线架模型的运动特性进行分析以保证机构满足设计需求；然后根据建立的三维模型动力学仿真，分析该机构的受载情况；最后形成设计方案。

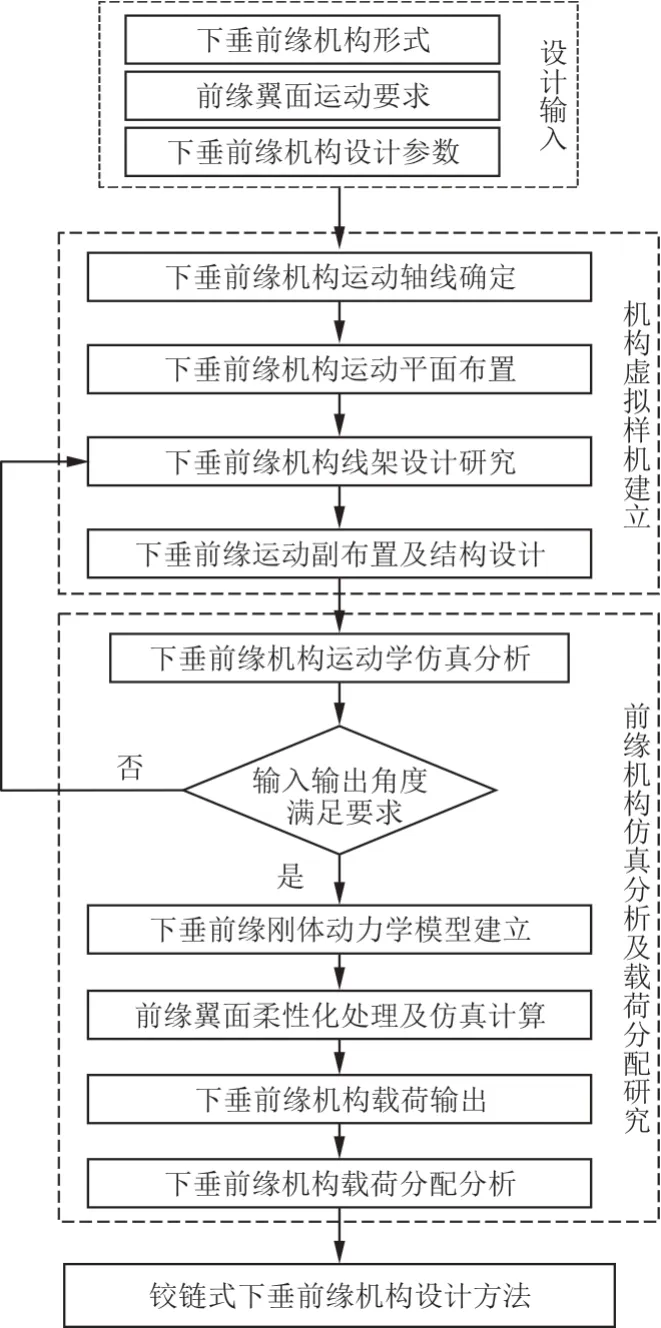
图1 铰链式下垂前缘机构研究思路Fig.1 Research ideas of hinged drooping leading edge mechanism

1.2 铰链式下垂前缘机构运动轴线确定

下垂前缘机构为绕固定轴的旋转运动，即前缘翼面上每个点都是在对应的圆弧上运动。因此根据前缘翼面的初始以及最终位置，结合下垂前缘机构的运动特点，采用几何解析法求解下垂前缘机构运动轴线：先在初始的翼面上选取两个参考点、，再从翼面运动后的位置上找到参考点运动后对应的点、，分别连接、和、，得到两条直线并求取其中垂面，两个中垂面交线即为机构的铰链轴线，如图2 所示。

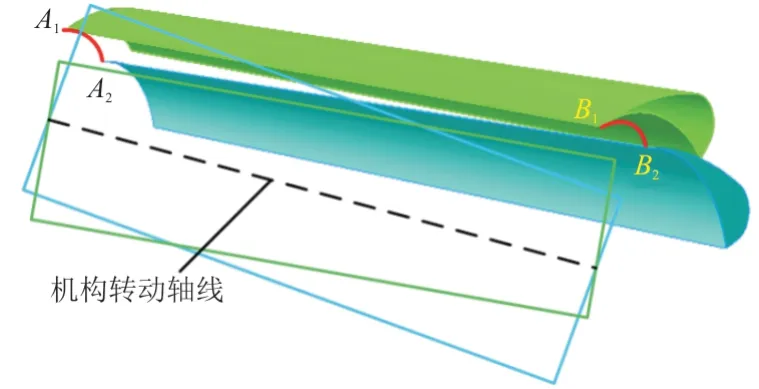
图2 下垂前缘机构几何解析图示Fig.2 Drooping leading edge mechanism geometric analytic graphics

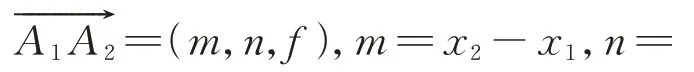
根据以上向量方程可以得到：

求解式（1）并用平面得到一般方程。

式 中 ：=；=；=；=-(++)。

同理可以求得的中垂面方程：

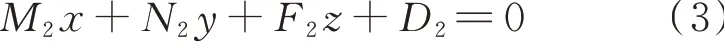
两平面不平行，则必相交于一条直线。联立式（2）和式（3），两式所表示的直线方程即为下垂前缘机构的铰链轴线，如式（4）所示。

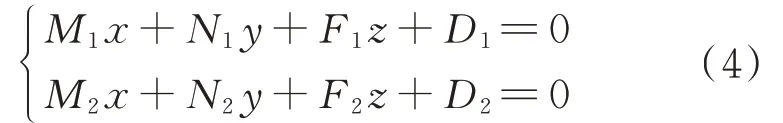
1.3 铰链式下垂前缘机构线架模型设计

下垂前缘机构的运动平面共5 个机构平面，分别布置在轴线的10%、30%、50%、70%和90%长度位置，以保证每套机构均匀承受气动力，包含2个驱动平面（30%和70%位置）和3 个从动平面，且与机构转轴垂直。下垂前缘机构的驱动平面为四连杆机构，如图3 所示，其中为驱动摇臂（主动杆），为驱动连杆，为从动摇臂（从动杆），代表翼盒（机架），采用四连杆机构的设计方法进行尺寸计算。

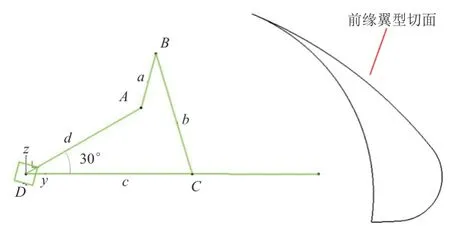
图3 下垂前缘驱动机构简图Fig.3 Sketch of the driving mechanism of the drooping leading edge

对于铰链四杆机构，如图4 所示，各点位可以与驱动机构的点位相互对应。

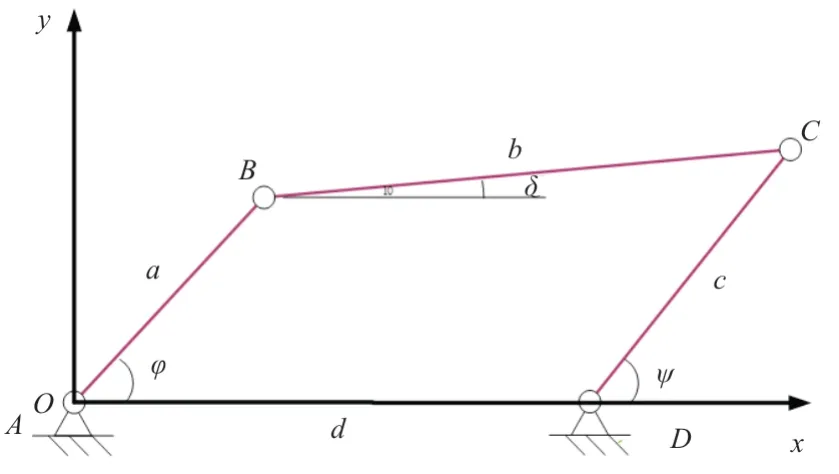
图4 四连杆简图Fig.4 Sketch of the four-link

通过图4 中构件向两坐标轴的投影得到式（5）和式（6）。

式中：为驱动杆与机架夹角；为从动杆与机架夹角。

将式（5）和式（6）分别平方后相加，消去得到：

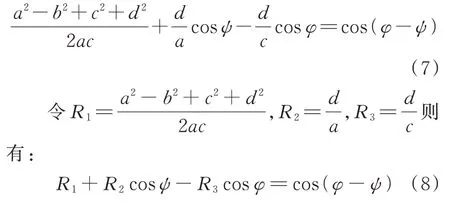
下垂前缘四连杆机构的设计输入数据如表1所示。将下垂前缘收放状态的、和相应的驱动杆长度、机架长度代入、、的计算公式，可以得到下垂前缘机构从动摇臂和连杆的长度。得到计算结果：=380.338 mm；=500 mm。这套机构的尺寸设计方案理论上可以实现在驱动摇臂转动90°的情况下，从动摇臂转角为26°。

表1 下垂前缘驱动机构初始尺寸设计输入Table 1 Design input of initial dimensions of the drooping leading edge driving mechanism

将初始驱动机构尺寸作为2 号驱动机构平面的驱动机构尺寸，同时对外侧4 号机构平面的驱动机构尺寸进行等比例缩放，以解决实际应用中机构安装空间沿展向向翼尖逐渐缩小的问题。对应2 号机构平面与4 号机构平面的各杆件长度比例为1∶0.9，同时在两个驱动机构平面内侧布置了侧撑杆，下垂前缘机构几何外形设计如图5 所示。

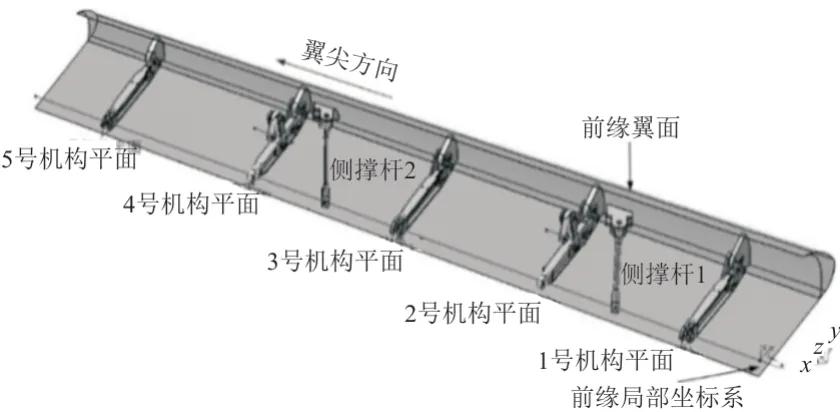
图5 下垂前缘机构几何外形设计Fig.5 Drooping leading edge mechanism geometric shape design

2 运动特性分析

在线架模型的基础上，主要对铰链式下垂前缘机构的驱动平面的四连杆机构进行运动特性分析，驱动机构简图如图3 所示，铰链式下垂前缘驱动机构采用封闭四连杆机构进行传动，该四连杆机构的最短杆为连架杆，即为曲柄摇杆机构。对于曲柄摇杆机构，最小传动角出现在主动曲柄与机架共线的两位置之一处，和中的较小的即为。

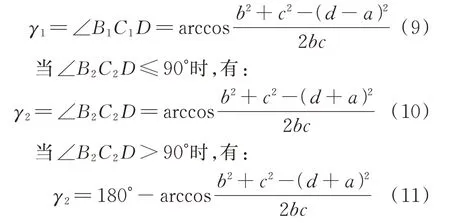
将下垂前缘机构中各杆的长度信息带入式（9）、式（10），可以得到=26°，=79°，由于2 个驱动机构的四连杆机构杆长是等比例的，即下垂前缘的2 个驱动机构均不存在死点位置。利用运动仿真软件，测量下垂前缘机构实际运动过程中的传动角变化情况如表2 所示，下垂前缘机构的设计只需要驱动臂转动90°即可，可以看出：在整个过程中传动角≥67.22°，说明下垂前缘机构的传力性能良好，且下垂前缘机构驱动臂转动至45°时，主动曲柄（驱动臂）与机架共线，此时传动角为79.27°，与理论计算结果一致。

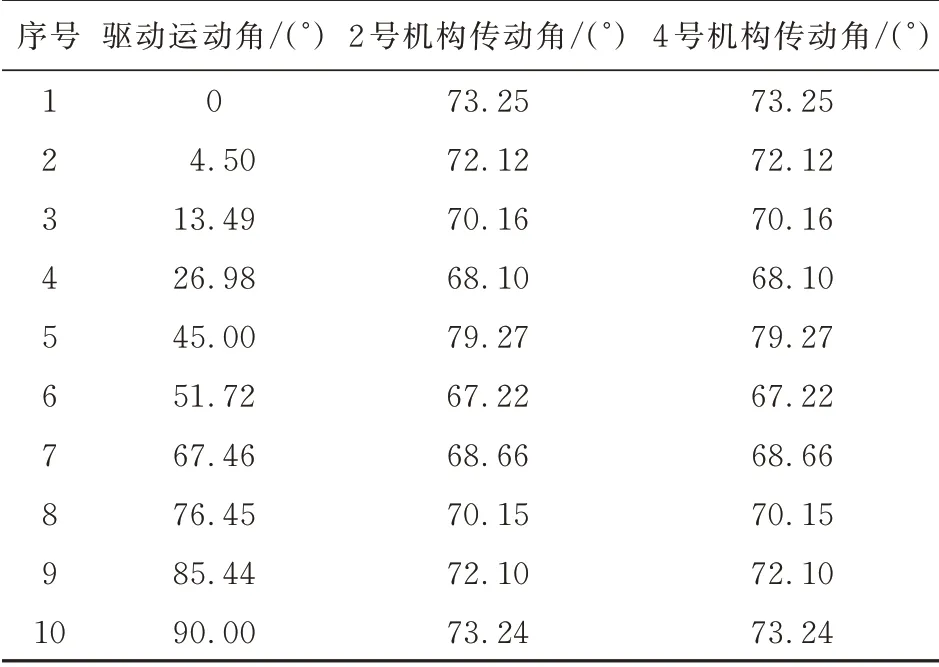
表2 下垂前缘机构实际运动过程中的传动角变化Table 2 Change of transmission angle during actual move⁃ment of the drooping leading edge mechanism

在下垂前缘机构运动仿真过程中，得到了下垂前缘机构的驱动臂和摇臂角度变化数据，各机构平面从动摇臂转角输出数据如表3 所示，其中2号和4 号驱动为输入信息，其他均为输出信息。当下垂前缘机构驱动摇臂向下进行90°的旋转时，各个机构平面的从动摇臂机构均可以实现下偏26°，与理论计算结果一致，且2 个驱动臂以及5 个从动摇臂的转动角度变化在运动过程中保持一致，说明下垂前缘机构在运动过程中5 个机构平面之间不存在运动干涉，均正常工作。针对下垂前缘机构所设计的曲柄摇杆机构，曲柄在90°的运动范围内，该连杆机构无明显的急回运动，即在下垂前缘机构中驱动臂做匀速转动时，能够保证翼面做平缓的下垂运动，从动摇臂运动角度随驱动臂输入角度变化如图6 所示。

表3 下垂前缘机构的驱动臂和摇臂角度变化数据Table 3 Angle data of the drive arm and rocker arm of the drooping leading edge mechanism

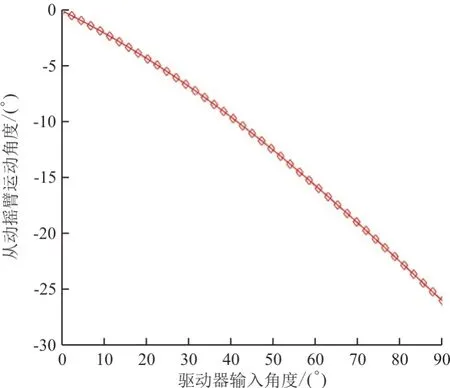
图6 下垂前缘机构输出参数信息Fig.6 Output parameter information of droop front mechanism

3 动力学仿真分析

在动力学仿真软件Motionvieww 建立下垂前缘机构的动力学模型，并将刚度较小的前缘翼面柔性化处理，柔性化处理包含前缘翼面结构初步设计、前缘翼面网格设置和有限元模型边界调节设置等建模工作，并输出前缘翼面结构的模态计算文件。在全刚体的动力学模型中进行翼面柔性体文件的替换从而进一步完成刚柔耦合动力学模型，结构材料选用铝合金7050。下垂前缘机构的局部坐标系如图7 所示，以前缘机构运动轴线为轴方向、以机翼参考平面的法线方向为轴方向。两套驱动机构（2、4 号驱动平面的曲柄）运动的下偏角度均为90°，在动力学模型中添加驱动角速度0.157 rad/s，下垂前缘机构的放下过程如图8 所示，0 s 为下垂前缘收起位置，10 s 时到达展开位置。

图7 下垂前缘翼面承力方向示意图Fig.7 Schematic diagram of the bearing direction of the drooping leading edge wing

图8 下垂前缘机构放下过程Fig.8 Releasing process of droop front mechanism

仿真计算得到驱动力矩变化情况如图9 所示，下垂前缘驱动力矩随驱动角度的增大而不断增加，这是由于在下垂前缘机构放下的过程中，力臂在不断增大。2 号驱动机构与4 号驱动机构力矩的输出值在增加过程中也近似呈等比例的变化趋势，但是2 号驱动机构承受较大的载荷。两机构的驱动力矩变化平缓，表明该机构在运动过程中不存在卡滞，具有较好的传力特性。

图9 驱动力矩变化图Fig.9 Change of driving torque

2 号和4 号平面驱动摇臂铰链点运动过程中的最大载荷值和驱动力矩如表4 所示，两个驱动平面的最大驱动力矩的比值接近3∶2，可以看出：2 号和4 号驱动机构载荷分配均衡，两个驱动机构布置合理。

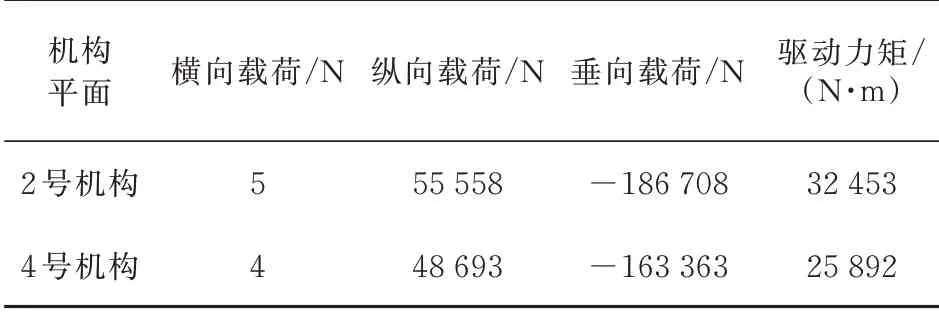
表4 下垂前缘机构驱动位置最大载荷输出Table 4 Maximum load output of the driving position of the drooping leading edge mechanism

在铰链式下垂前缘机构运动过程中，横向载荷受力变化如图10 所示。

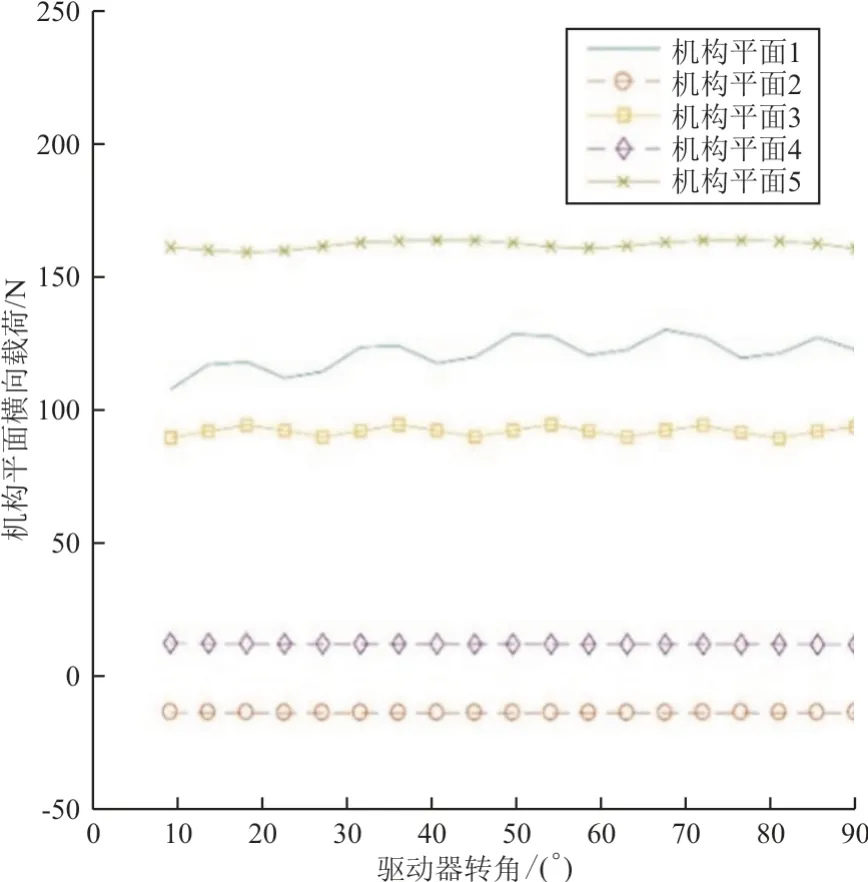
图10 铰链点横向载荷Fig.10 Lateral load at hinge point

从图10 可以看出：由于在2 号机构和4 号机构平面布置有侧撑杆，因此对应机构平面的驱动位置处的横向载荷较小，说明此方案可有效改善机构平面横向载荷的受力情况，尤其是有驱动机构处的横向受载，如表4 所示。

侧撑杆横向载荷变化如图11 所示，可以看出：在下垂前缘机构运动过程中，2 号机构平面的侧撑杆受载较大，与驱动力矩载荷分配相符。

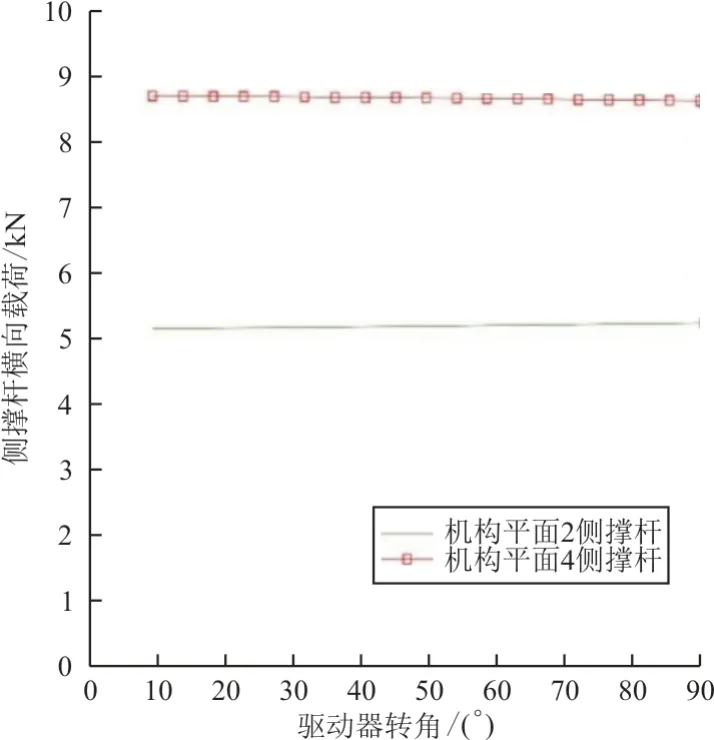
图11 侧撑杆横向载荷Fig. 11 Lateral load of side brace

4 结 论

（1）本文提出了一种基于四连杆形式的下垂前缘机构设计方法，得到了下垂前缘的机构型式。机构驱动臂能够匀速转动，铰链式下垂前缘能够平稳下偏26°，过程中无干涉卡滞。

（2）通过考虑下垂前缘翼面的变形，并实现翼面的柔性化，得到了下垂前缘机构的刚柔耦合动力学模型，最终利用仿真与计算得到了该机构运动过程中的驱动力矩和铰链点载荷，两个驱动平面的最大驱动力矩比值接近3∶2，该机构传力性能良好，载荷分配合理，并且侧撑杆很好地改善了驱动处的载荷状况，由此验证了本文所提出的设计方法的可行性和合理性，该设计方法具有良好的应用前景。