用建模思想培养学生分析问题能力的几点思考
2022-02-22张长利
张长利
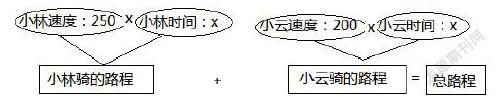
摘要: 《义务教育数学课程标准》2011版中提出在数学课程中用数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识十个核心词阐释了应当注意发展学生哪些基本的数学素养。曹培英老师撰写的《跨越断层,走出误区》一书中说到:“数学模型”,目前尚无公认的定义,粗略来说,数学模型仍是针对或参照某种事物系统的特征和数学量关系,采取形式化的数学语言,概括地或近似地表达出来的一种数学结构,按广义解释,一切数学概念,数学理念体系,各种数学公式,各种方程以及由公式系列构成的算法系统等,都可以称之为数学模型。狭义解释,只有那些反映特定问题或特定的具体事物系统的数学关系结构,才叫做数学模型。这也是当今应用数学中数学模型的原意。“建模”是数学发展最初的原动力,模型思想的建立,是学生体会和理解数学与外部世界联系的基本途径,数学建模,是一种特殊的数学问题解决形式。
关键词:建模思想;分析能力;思考
从教二十多年,听了不少教师上解决问题的课堂教学,从教学过程的设计流程来看,大致可以归纳为:1.创设情景,提出问题,2.引导读题,分析问题(主要是分析理解部分关键词、句的意思),3.引导学生说出解答方法,列式解答,4.根据结果回顾反思,检查计算结果是否正确,5.做相应的练习巩固。
那么怎样才能通过课堂的引领,让学生真正建立起应用题的逻辑模型分析结构呢?学生在这种逻辑模型分析结构的帮助下,有入情入景的思维进程,就不会凭表面的感觉来错误地解决问题了。为此,我有几下几点思考:
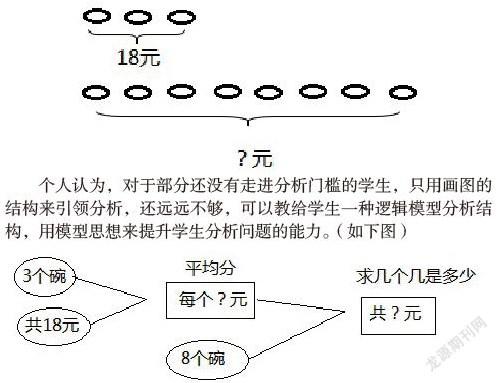
1.结合对应用题文字的理解,画象形图或线段图,引领学生寻找有联系的数量,求出相应的数学问题,画出分析模型结构,逐步逼近最后问题的解决。如:小学数学三年级上册六单元多位数乘一位数,学生学习了笔算方法后,都有相应数学问题解决板块呈现,在71页例8,妈妈买了3个碗,用了18元,如果买8个同样的碗,需要多少钱?这是典型的归总问题,但对于小学中低段的学生,这些莫生的概念,不能给他作过多的解释,怎么才能不机械地把学生带入到分析中来呢?有的老师采用了画象形图来帮助理解:(如图)
个人认为,对于部分还没有走进分析门槛的学生,只用画图的结构来引领分析,还远远不够,可以教给学生一种逻辑模型分析结构,用模型思想来提升学生分析问题的能力。(如下图)
由“3个碗”和“共18元”,能求出什么问题?怎样计算?由“每个碗6元”和“8个碗”又能求什么问题?怎样计算?有了这样逻辑模型引领分析,学生仿佛带上一盏灯,去寻找相关的两个条件,逐步求出最后的问题,解答的方法也水到渠成。也可以反过来由最后的问题入手,去寻找解决问题需要的哪两个条件,哪个条件没有直接告知,又需要寻找哪两个条件解答出来。这样的逻辑模型结构,比教材中给我们呈现的由阅读与理解→分析與解答 →回顾与反思这一模型结构更形象具体一些,并富有操作性。有了这样的逻辑分析结构引领训练,学生的逻辑分析能力才会真正得到锻炼和提高。
2.在理解掌握了一些基本的数量关系后,可以结合具体的数量关系模型结构来进行分析,提高学生分析问题的能力。如:人教版五年级上册学生在学习简易方程中的解决问题例5:小林家和小云家相距4.5km。周日早上9:00两人分别从家骑自行车相向而行,两人何时相遇?这是学生在理解了速度、时间、路程数量关系后,进行的相遇问题的学习。教材在进入分析与解答步骤时,采用画线段图这种半抽象的模型结构引领学生进行分析,得出模型结构:小林骑的路程+小云骑的路程=总路程,个人认为只对于学优生来说,不会有什么困难,对于学困生来说,为什么要想小林骑的路程和小云骑的路程?是怎么思考的?它们的路程与总路程之间是什么关系?这些问题,如果没有逻辑模型思考,学困生的思路一般不容易跟上,导致最后列出方程的模型解答不容易理解。可以在画图模型的分析上,结合前面学习理解的速度、时间、路程数量间的模型结构关系,帮助学困生小步走分析,提升他们的分析问题的能力。如下图:
解:设两人x分钟后相遇。
3.根据具体的问题情景,可以用具体的动作演示加上文字的描述,建立情景模型,让学生置身事件本身,提升理解能力。还是人教版五年级上册学生在学习简易方程中的解决问题例5:小林家和小云家相距4.5km。周日早上9:00两人分别从家骑自行车相向而行,两人何时相遇?在学生理解文字题意后,叫学生演示相遇问题情景模型结构,同时出发,骑1分钟,按下暂停键,学生观察小林骑了多远?小云骑了多远?两人相距多远?骑2分钟,按下暂停,学生观察小林行多远?小林行多远?随着时间的变化,两人相距的距离在逐步缩短,最后相遇时相距为0,把学生置于事件本身的情景模型中,才能真正理解相遇问题究竟是怎么回事,不会导致以后机械应用公式模型套用解答。
在实际教学中教师应尽可能留给学生更多的空间和时间去演绎问题的情景结构或数量关系结构,用模型结构去提高学生逻辑分析能力,让孩子真正走进解决问题的分析过程,这样才是真正有效的课堂,高效的课堂。
参考文献:
[1]薛建忠.数学建模思想在小学数学教学中的应用研究[J].中华少年,2017(36):176-177.
[2]陈旭.浅谈小学数学建模中的几个问题[J].山东教育,2019(07):50.
