复杂环境中煤矿智能机器人巡检路径动态规划

闫萍

(开滦(集团)有限责任公司，河北，唐山 063018)

0 引言

随着工业自动化水平的不断提高，智能机器人在煤矿勘测、运输与救援等方面发挥着越来越重要的作用[1]。在复杂的矿井环境中，机器人依靠自主导航技术实现自由运动，因此该技术中的路径规划算法决定了智能机器人的移动路径的合理性和移动效率[2]。传统的动态窗口算法虽然应用较为普遍，但其所规划的路径较长，规划速度较慢且实时性较差，严重影响了机器人的工作效率[3]。为此，提出了一种负载环境中煤矿智能机器人巡检路径的动态规划算法，通过空间粒子最佳位置的选取确定下一时间段机器人的最佳移动速度，从而有效提高了智能机器人在复杂环境中所规划移动路线的合理性。

1 DWA算法原理

对于智能机器人在所处环境中的运动方式，传统DWA动态窗口法(Dynamic Window Approach)的驱动原理是根据机器人的具体位置和移动速度设定范围，将其路径规划过程转换为对移动速度进行选择的过程，以最合理运动轨迹下的移动速度作为决定下一个时间段驱动力大小的依据[4]。

首先，机器人依据整体运动环境和自身移动速度的限制来约束采样速度。其速度的设定区间[5]如式(1),

Va={(v,ω)|0≤v≤vmax,-ωmax≤ω≤ωmax}

(1)

式中，v，ω分别表示机器人移动过程中的线速度和角速度，vmax，ωmax则分别表示线速度与角速度的最大值。

在不同大小的驱动力矩作用下，机器人的加减速度也被限制在一定范围内，因此，在长度固定为θt的间隔时间段内，机器人最高移动速度的变化区间为式(2),

Vg=(v,ω)=

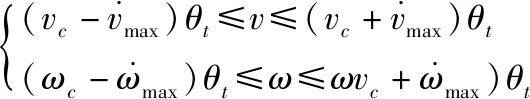
(2)

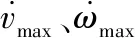
为了避免机器人在移动过程中与障碍物发生碰撞，必须保证机器人在接近障碍物之前即停止运动，在此条件下其移动速度限定区间[6]表述为式(3),

(3)

式中，dist(v，ω)代表当前规划路径上障碍物与机器人之间的距离。

综合以上速度约束条件，机器人的移动速度集合应为式(4),

Vf=Va∩Vg∩Vz

(4)

完成速度采样，然后在以上速度集中以固定的行进速度进行采样，通过评价函数对采样效率进行评价为式(5),

(5)

式中，heading(v，ω)表示机器人在当前采样速度下移动至某一段规划路径的端点时机器人行进方向与整条路径终点之间的角度差，velocity(v，ω)表示从采样速度中提取的线速度，a，β，γ均为权值参数，为了使三者的中权重较为接近以保证评价质量，在进行速度评价之前对它们进行归一化处理，使其数值落在[0，1]区间内。

在a=0.4，β=0.2，γ=0.4的条件下，利用评价函数H对机器人的移动速度集[(0,2)m/s，(-50,50)rad/s]进行评价，H值最大时所对应的(v，ω)便可作为下一个时间段机器人的移动速度。通过DWA算法获取的机器人规划路径如图1所示。图1中圆形与正方形黑色物体为路径上的障碍物。由图1中的轨迹可见，当障碍物分布较为密集时机器人智能绕开该区域，由此增加了机器人运动路径的总长度。

图1 通过DWA算法得到的机器人规划路径

2 算法优化设计

利用上述评价函数对速度采样空间进行评价是一个较为漫长的过程，因此，在复杂的环境中，基于DWA算法的机器人行进路径过长，且机器人规划路径的效率很低，不能及时获取最优速度，造成环境中存在障碍物密集分布区域时机器人无法规划出合理的行进路径。本文基于膜计算(Membrane Computing,MC)和粒子群(Particle Swarm Optimization,PSO)的MCPSO-DWA算法对传统DWA算法进行优化，缩短机器人的行进路程，提高其工作效率。

2.1 设计思路

首先将机器人的移动速度空间Vf转换为以线速度v为横坐标、角速度ω为纵坐标的二维坐标空间[6]，转换后的坐标空间如图2所示。其中，(vmin，vmax)与(-ωmax，ωmax)分别表示机器人的移动速度约束范围，阴影区域S表示机器人的速度限制区间。在这里引入粒子群算法，那么S就对应成为算法中的粒子搜索区间，而(vmin，vmax)以及(-ωmax，ωmax)则对应该区间的边界，S中的任意一点(v，ω)对应粒子在坐标空间中的位置X。在坐标空间中X持续更新，最后依据最优粒子的位置得到最优移动速度(v，ω)。

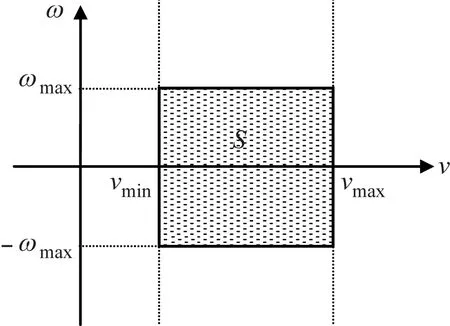
图2 速度限制坐标空间

构建一个由m个基本膜和1个表层膜所组成的单层膜。在速度限制区域S中提取出Q个粒子，其中每个粒子的位置都对应一个机器人在某个时间段内的移动速度(v，ω)，粒子位置与移动速度的原始表达式分别为式(6)和式(7)。

X=[(vmax,ωmax)-(vmax,-ωmax)]×r+(vmax,ωmax)

(6)

V=[(vmax,ωmax)-(vmin,ωmin)]×0.1×(2r-1)

(7)

式中，r为一个随机数，其取值区间为[0,1]。

将Q个粒子等分为m份(每份粒子数量为D)并注入每个基本膜中，设包含在第k(k=1，2…，m)个基本膜中的第d(d=1，2…，D)个粒子的初始位置为Xkd，初始速度为Vkd，通过式(5)评价基本膜中的粒子，依据评价函数值找到每个基本膜中的最优粒子，再将m个最优粒子发送到表层膜进行对比，由此得到整个粒子群中的最优粒子，表层面将该粒子信息返回给各基本膜，基本膜中的粒子参照群中最优粒子的位置和速度进行更新，以此形成整个粒子群的反复迭代更新，直至得到最优粒子位置，即可确定机器人在下一个时间段内的移动速度。在每一个固定间隔的时间段内机器人都以最优速度行进，直至到达路径终点。

2.2 算法实现流程

本文所提出的改进后的算法实现流程如下。

步骤一：智能机器人依据自身的驱动能力和所在环境的复杂性设定速度限制区间Vf。

步骤二：完成速度限制区间向二维坐标区间的转换。

步骤三：构建单层膜，从限制区域S中提取出Q个粒子，通过式(6)和式(7)计算粒子的位置和移速，等分到各基本膜中，在这里需要分别对迭代次数N、惯性权重ωmin和ωmax、学习因子c1和c2、适应度函数阙值δ进行设置[7]。

步骤四：利用式(5)对各基本膜中的粒子进行评价，得到所有粒子的适应值H0kd，即粒子在基本膜中的历史最优评价分数Pkdbest，将所有粒子的Pkdbest进行对比，得到最高评分的即为该基本膜中的最优粒子Gkbest。

步骤五：按照既定规则Rk将各基本膜中的Gkbest发送到表层膜并互相进行比较，其中评分最高的即为粒子群中的最优粒子Gbest。

步骤六：按照既定规则R′k将Gbest信息返回给各基本膜，膜中的各个粒子按照式(1)和式(2)进行位置和速度的更新。

步骤七：再次对基本膜中的粒子进行评价，更新Pkdbest和Gbest，得到较之前更优的粒子。

步骤八：通过反复迭代持续更新粒子群，直到迭代到第N次或Gbest的适应值为δ，依据当下时刻Gbest粒子的坐标值得到机器人在下一个时间段内的移动速度[8]。

步骤九：机器人按输出的速度行进并判断是否已到达路径终点，若已到达则停止行进，反之则由步骤一进入下一个时间段移动速度的计算流程[9]。

算法流程见图3。

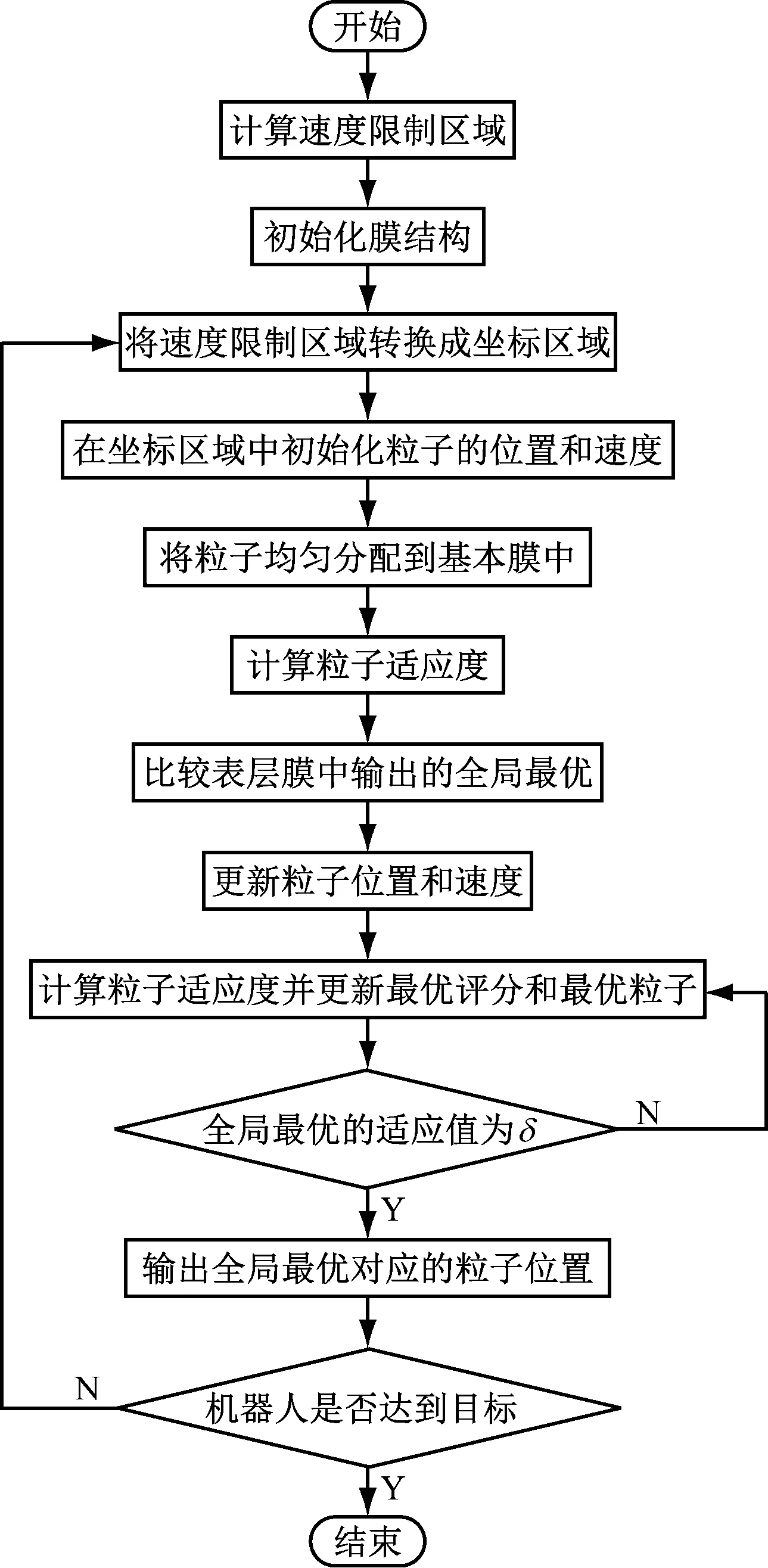
图3 算法流程图

3 实验及结果分析

为了验证本文所提出算法的有效性和性能优势，在复杂程度不同的多种环境中将本文算法与传统DWA算法的性能进行对比，考察煤矿智能机器人的行进路程长度、行进时间和穿越障碍物密集分布区域的能力。

3.1 实验参数

仿真实验在Python3.7软件环境中进行，机器人的工作环境按图2的形式设定。本文所提出算法的具体参数设定如表1所示。从速度坐标区间的粒子群中提取出20个粒子，基本膜数量为4个，每个基本膜中分配5个粒子。传统DWA算法的具体参数设定如表2所示，障碍物半径设定为0.5 m。

表1 本文算法的参数设定

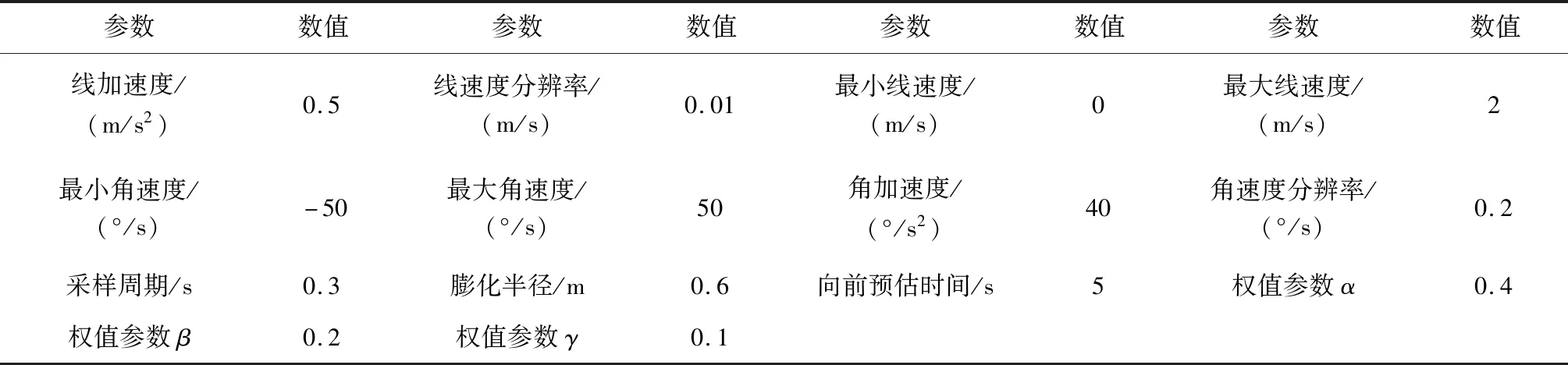
表2 参数设定

3.2 实验结果与分析

首先在复杂程度不同的4种环境中验证本文算法MCPSO-DWA的性能，环境复杂度由低到高，其中的环境3和环境4障碍物分布密度较大(障碍物8个以上)。机器人在上述各种环境中分别基于DWA算法和本文算法所规划出的最优路径如图4所示。由图4(a)和图4(b)可见，在相对简单的环境中，通过2种算法所规划的路径都能从障碍物间穿过，路径都较为合理且长度基本接近。而在图4(c)和图4(d)所示的复杂环境中，本文算法所规划的路径能够使机器人安全穿越障碍物，相较于DWA算法明显更为合理。

2种算法下规划路径的分段数量和每一段的评价次数如图5所示。由图5(a)和图5(b)可见，在环境1和环境2中DWA算法所规划的路径分段数分别为58个和75个，结合表2中设定的参数，每一段都会完成800次评价；在同样环境中本文算法所规划的路径分段数分别为64个和70个，每一段都的评价次数为粒子群算法中G best的适应值为(时迭代次数与粒子数量的乘积。由图5(c)和图5(d)可见，在环境3和环境4中法所规划的路径分段数分别为76个和124个，相比DWA算法分段数量有所减少，可见本文算法能够提升机器人的行进速度。

本文算法的路径分段数量与每一段迭代次数的关系如图6所示。由图中的折线形式可见，在环境1和环境2中本文算法每一段路径的迭代次数范围为5-30，结合图5(a)和图5(b)可得每一段得评价次数为100-600，均少于DWA算法对应的数值。在环境3和环境4中,本文算法每一段路径的迭代次数范围为10-35，结合图5(c)和图5(d)可得每一段的评价次数为200-700，均少于DWA算法对应的数值。

通过2种算法所获取的规划路径的具体数据如表3所示。表中数据显示，在最简单的环境1中，本文算法在总行进时间和路径分段数量上与DWA算法较为接近，但路径总长度相较于DWA算法缩短了8.77%；环境2和环境3的复杂度有所增加，本文算法规划路径所需的时间比DWA算法分别减少了8.66%和15.53%，同时规划路径总长度也缩短了2.3%和6.71%；在最为复杂的环境4中，本文算法的路径分段数量比DWA算法少41个，规划耗时减少了31.55%，路径总长度缩短了10.02%。

表3 2种算法所得规划路径具体数据

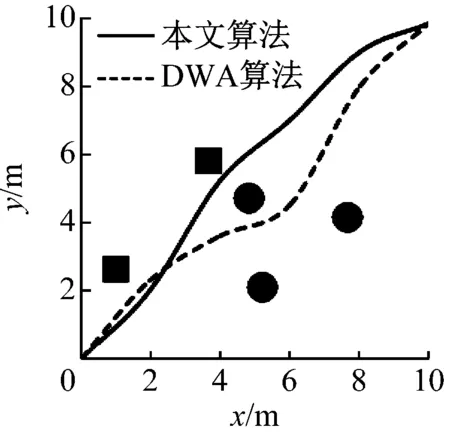
(a)环境1

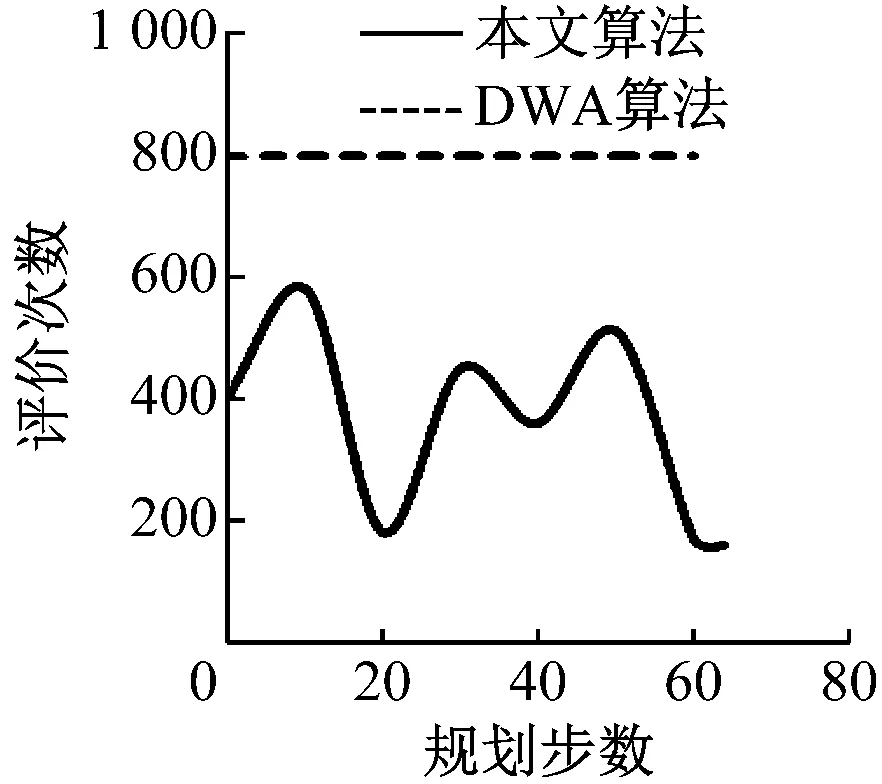
(a)环境1

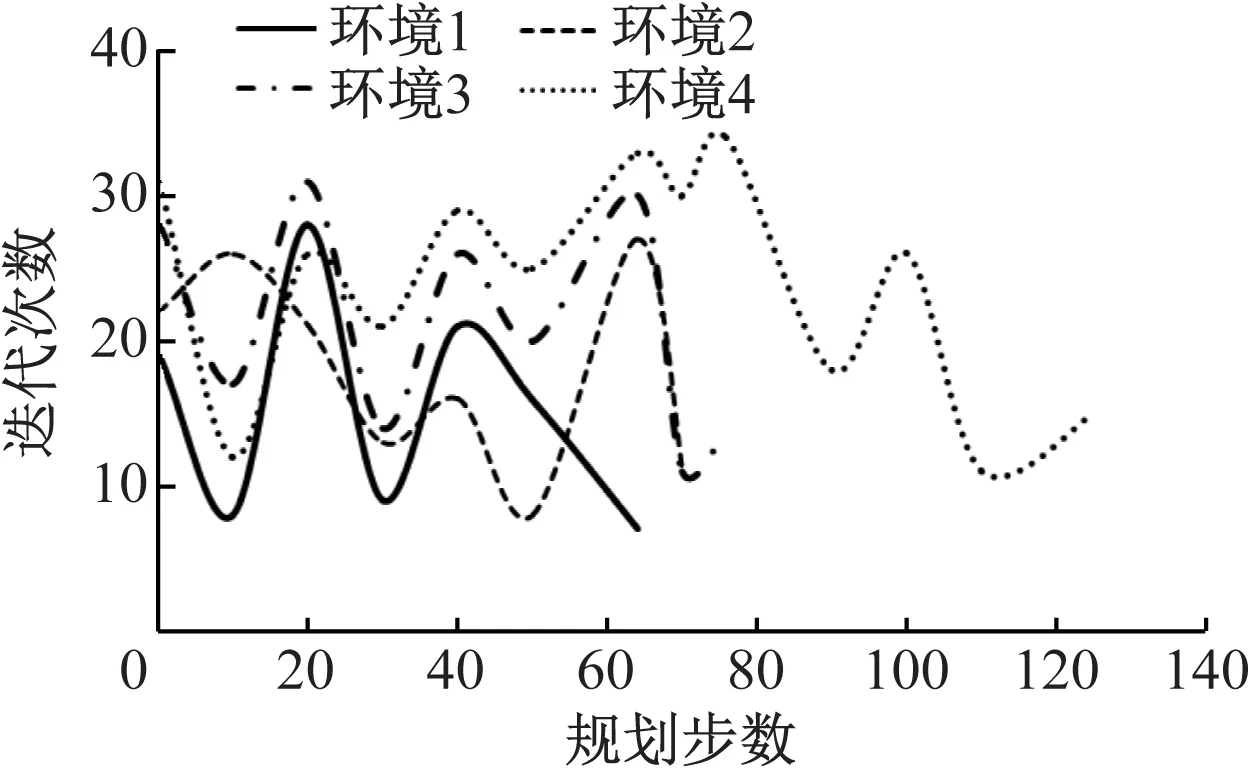
图6 本文算法下路径分段数量与评价迭代次数的关系

在4种环境中机器人的移动速度统计如图7所示。由图7可知,在最简单的环境1中，2种算法下机器人的行进速度存在一定差距，DWA比本文算法快0.12 m/s；但随着环境复杂程度的增加，在其余3种环境下均是本文算法的行进速度更快，分别比DWA算法快出0.05 m/s、0.08 m/s、和0.19 m/s，说明本文算法在复杂环境种比DWA算法拥有更高的行动效率。

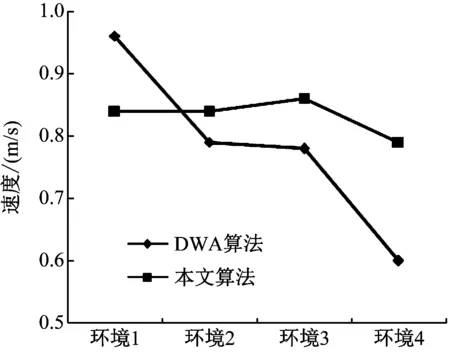
图7 2种算法下机器人的移动速度

在障碍物呈U型分布的环境中，基于其它算法智能机器人所规划的路径常常被阻断，现有研究结果表明，A-DWA(Adaptive-DWA，自适应DWA)算法[10]具有适应性强、路径规划高度合理的特征，为了进一步验证本文算法MCPSO-DWA的性能优势，在包含U型分布障碍物的环境中对本文算法、A-DWA算法与DWA算法规划的路径进行对比，3种算法的规划结果如图8所示。

图8 包含U型分布障碍物环境中3种算法规划的行进路径

由图8可见，A-DWA算法和DWA算法均与障碍物发生碰撞，机器人的行进路径被中断，而本文算法则能够成功引导机器人绕过U型障碍物分布区域并最终到达目的地。由此可以证明本文算法能够满足引导智能机器人在高度复杂的环境中规划合理行进路径的需求。

4 总结

为了解决基于传统DWA算法的煤矿智能机器人在复杂环境中所规划的行进路径不合理、工作效率较低的问题，提出了一种优化的动态规划算法MCPSO-DWA，将机器人的速度限制空间转换为能够标示粒子位置的二维坐标空间，引入粒子群算法在膜计算中优化了机器人移动速度的限制区间，有效提高了机器人路径规划的合理性和规划效率。通过仿真实验证明，本文所提出的算法相较于其它同类算法具有明显的性能优势，适于在煤矿智能机器人的自主导航系统中应用和推广。