P掺杂6H-SiC的第一性原理研究

黄思丽，谢 泉，张 琴

(贵州大学大数据与信息工程学院,新型光电子材料与技术研究所，贵阳 550025)

0 引 言

SiC是由Si和C组成的应用广泛且经济实用的半导体材料[1-2]，具有优异的物理化学特性和电学特性[3]，如禁带宽、化学性质稳定、导热系数大和漂移速度快等优点[4]。6H-SiC作为SiC中一种重要的多型体，具有结构最稳定、击穿电子最强、电子迁移速度最快等特点而备受研究者关注[5]。

近几年来，无论是在实验或理论方面，6H-SiC材料的研究依然备受关注。很多学者对6H-SiC进行了掺杂研究，如杨昆等[6]使用物理气相传输法制备出Ti掺杂6H-SiC衬底经过热处理电阻率从小于105Ω·cm可增至1010～1011Ω·cm。Zhou等[7]采用V掺杂6H-SiC单晶衬底制备出了大功率光电开关，黄毅华等[8]计算了Al掺杂6H-SiC的磁性源于C原子的p轨道电子。Lin等[9]计算了N掺杂6H-SiC，得出本征和N掺杂6H-SiC均未表现出磁性，但 N和Si空位共掺表现出反铁磁性。Nie等[10]研究了N、V掺杂6H-SiC晶体的载流子动力学和机理。张明军等[11]研究了Al单独掺杂6H-SiC 中的Si或C磁性微弱，共掺Si与C表现出强烈的磁性。臧源等[12]计算了Ge掺杂6H-SiC的电学与光学特性。邹江等计算了La[13]、Ce[14]掺杂6H-SiC的电子结构与光学性质，王熠欣等[15]计算了Mn掺杂6H-SiC的第一性原理研究。以上Ge、La、Ce以及Mn掺杂可有效改善6H-SiC的电子结构与光学性质。Pinheiro等[16]对P掺杂6H-SiC进行了磁共振研究，但并没有对P掺杂6H-SiC理论计算方面进行研究，且以往掺杂研究多集中于其磁性，对6H-SiC光学性质方面的理论研究较少，因此本文采用基于密度泛函理论的赝势平面波法计算分析未掺杂与P替换Si、C以及间隙掺杂6H-SiC电子结构以及光学性质[17]。结果可为6H-SiC材料在光电领域的应用提供理论依据。

1 模型与方法

如图1(a)所示稳定的6H-SiC为”ABCACB”型六方密堆积结构[18]，空间群为P63mc[19]，晶格参数a=b=0.309 5 nm，c=1.517 nm, 在晶胞的基础上，向a与b基矢方向扩充一倍，得到2×2×1含有48个原子的超晶胞，并进行本次计算，体系中Si与C的原子数比例为1∶1。采用一个P原子替换一个Si原子，或替换一个C原子以及P间隙进行掺杂6H-SiC，三种掺杂方案模型图如图1所示。

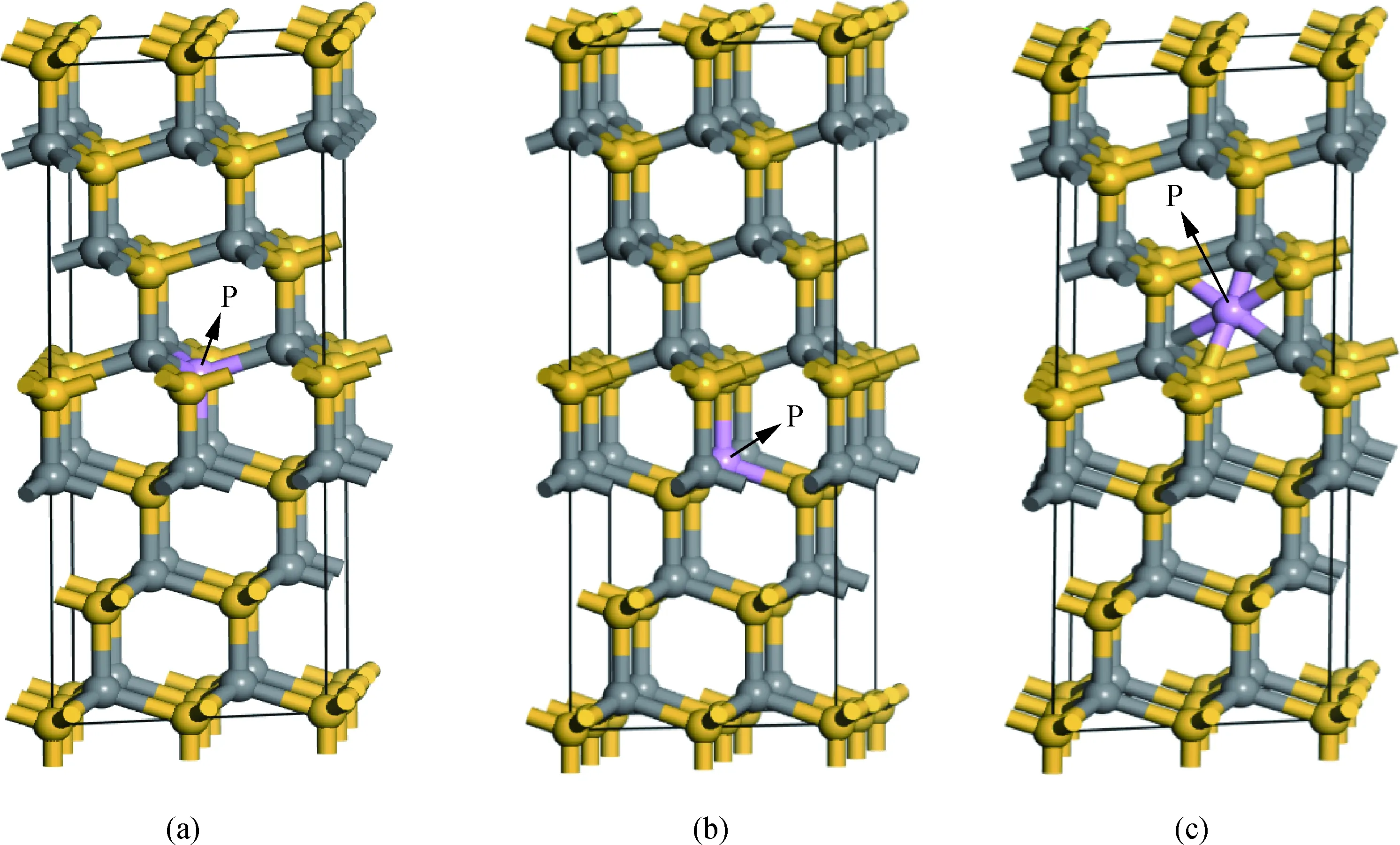
图1 P掺杂6H-SiC的超晶胞模型：(a)P替换Si;(b)P替换C;(c)P间隙掺杂Fig.1 Supercell model of P-doped 6H-SiC: (a) P substituting Si; (b) P substituting C; (c) P interstitial doping

计算采用基于密度泛函理论(DFT)从头计算方法，选用Materials Studio8.0中的CASTEP软件包对未掺杂与P替换Si、C以及间隙掺杂6H-SiC的晶体进行结构优化[20]，经过收敛测试最终选定截断能与网点设置分别为420 eV与3×3×1，收敛精度设置为5.0×10-4eV/atom,优化完成后再进行能带结构、态密度以及光学性质的计算。

2 结果与讨论

2.1 几何结构

由表1可知未掺杂的6H-SiC优化所得结果与实验结果接近，表明计算模型与计算方法是合理的。由于P与Si右邻，它们的电子结构与原子半径相似，因此P替换Si掺杂6H-SiC得到的晶格常数与晶胞体积变化不大。而P替换C掺杂由于P原子半径(0.111 nm)大于C原子半径(0.075 nm)，因此P替换C掺杂6H-SiC所得的晶格常数与晶胞体积变大。P间隙掺杂后体系中额外多了一个P原子，因此晶体的晶格常数与晶胞体积均膨胀变大。

表1 掺杂前后6H-SiC晶格常数、晶胞体积与掺杂形成能Table 1 6H-SiC lattice constant, unit cell volume and doping formation energy before and after doping

为了了解P替换Si、C以及P间隙掺杂6H-SiC的稳定性，进行了三者掺杂形成能的计算。形成能计算公式[21]如式(1)所示：

Eform=Etot(P∶6H-SiC)-Etot(6H-SiC)-nPμ(P)+nxμ(x)

(1)

式中：Etot(P∶6H-SiC)表示P掺杂6H-SiC的总能量；Etot(6H-SiC)表示未掺杂6H-SiC的总能量；nP表示掺杂P原子的个数；μ(P)表示掺杂原子P的化学势；nx表示被替换原子Si或C的个数；μ(x)表示被替换原子Si或C的化学势。当进行间隙掺杂形成能计算时，因P间隙掺杂时未有原子被替换，故公式(1)中nxμ(x)项不存在。若计算Eform结果值为负时，说明掺杂反应过程中释放能量，反应较容易进行；若Eform值为正时，意味着发生反应过程中需要吸收能量，反应较难进行。Eform的值越小，证明其结构越稳定。从结果得出替换式掺杂比间隙式掺杂结构更稳定。

2.2 电子结构

2.2.1 能带结构

从图2(a)未掺杂6H-SiC原胞能带图看出，其价带顶与导带底位于不同位置，故为间接带隙半导体。类似情况，图2(b)超胞能带图中其价带最大值与导带最小值也位于不同点，因此超胞6H-SiC仍为间接带隙，带隙值为2.052 eV，与臧源等[12]计算结果一致，但比实验值3.02 eV[22]稍小。这是由于密度泛函的估计误差所引起，但对结果的总体趋势分析无影响。

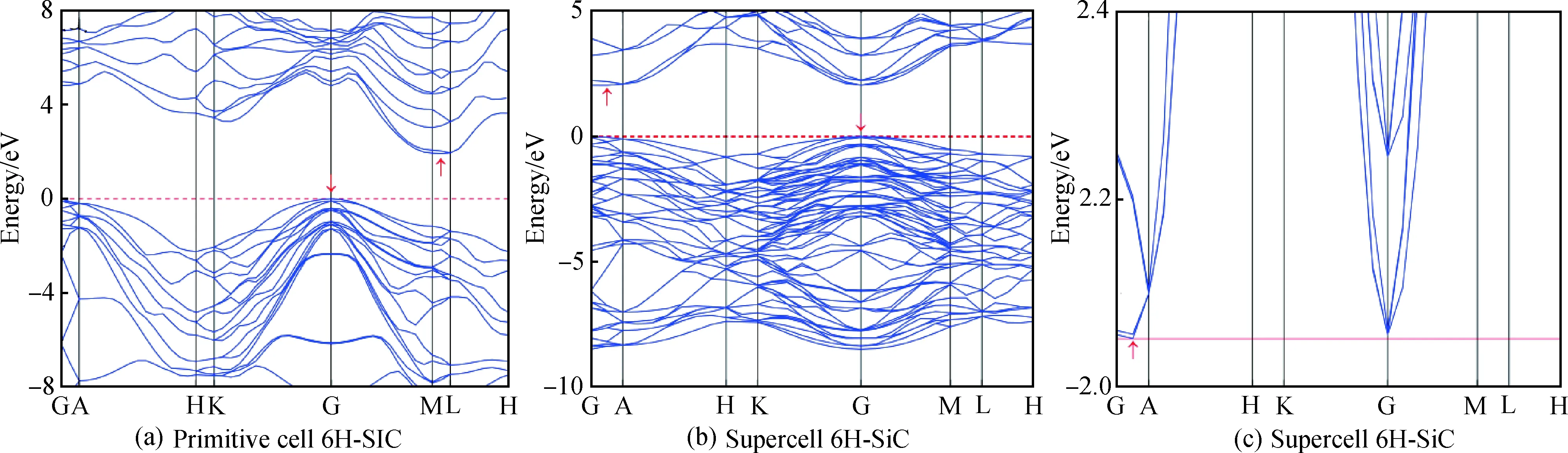
图2 未掺杂6H-SiC的能带图:(a)原胞;(b)、(c)超胞Fig.2 Band diagram of intrinsic 6H-SiC: (a) primitive cell; (b), (c) supercell

图3(a)与(b)为P替换Si、C掺杂的能带图。与未掺杂相比，在P掺入6H-SiC体系后，由于P比Si与C原子最外层多一个电子，故掺杂后可为导带底附近提供大量电子，使得导带与价带均向低能级移动，同时价带中能级数显著增多，两种替换掺杂使得费米能级移入导带，显然P替换Si、C掺杂6H-SiC导电类型为n型。图3(c)为P间隙掺杂6H-SiC的能带图，与未掺杂的对比，间隙掺杂后价带导带均下移，但出现一条价带向上移动并插入费米能级，形成施主能级并与费米能级重叠，部分施主杂质发生电离产生电子，费米能级下的受主能级提供空穴，即P的3p与C的2p。间隙掺杂中起主要作用的是费米能级下的受主能级，且空穴的产生大于电子的产生，间隙掺杂6H-SiC导电类型转为p型。如表2所示，P替换Si、C掺杂后的带隙值分别减小至1.787 eV和1.446 eV，间隙掺杂带隙减小幅度最大，为0.075 eV。带隙减小使得电子跃迁所消耗的能量减少，电子的跃迁加快，材料导电性增强。

表2 掺杂前后6H-SiC的带隙变化Table 2 Band gap change of 6H-SiC before and after doping

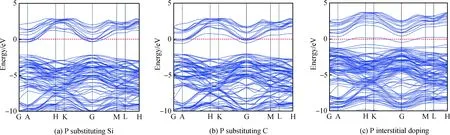
图3 掺杂后6H-SiC的能带图:(a)P替换Si;(b)P替换C;(c)P间隙掺杂Fig.3 Energy band diagram of 6H-SiC after doping: (a) P substituting Si; (b) P substituting C; (c) P interstitial doping

2.2.2 态密度

图4(a)为未掺杂6H-SiC的态密度图，在价带-15.6～-9.66 eV区域主要由Si 3s和3p以及C 2s态电子共同构成。在价带-8.81～0 eV区域Si 3s和3p以及C 2p态电子贡献最多，其中Si 3s和3p形成sp3轨道杂化，导带部分由Si 的3p贡献大部分电子，Si的3s以及C的2s、2p态电子贡献小部分电子。其中C的2s与2p形成sp3杂化轨道。

图4(b)为P替换Si掺杂的态密度图，在-17.7 eV以及-10.8 eV处出现P 3s峰，局域性较强。P替换Si掺杂后使得P原子周围的Si与C原子态密度发生变化，因Si和C与P重组成键，故部分态密度局域性减弱。P引入的 3p态电子易在导带中形成游离电子(施主)；P 3p与Si 3p共同作用使得态密度向低能级偏移。由图4(c) P替位C掺杂后的态密度图看出，邻近P的Si与C原子态密度发生变化较小，由于P的掺入在导带附近提供3p电子，同样由P 3p与Si 3p作用使得态密度整体向低能级偏移。图4(d)为P间隙掺杂态密度图，P间隙掺杂对周围的Si与C原子影响比较大，由图看出在-16.4 eV处出现了C的2s峰与P 3s峰，价带部分Si 3p与C 2p态密度明显下降且向费米能级移动，P 3p分裂为两部分，分布在价带顶与导带底附近，费米能级附近态密度显著增强，产生了与费米能级重合的施主能级，故而影响各电子态之间的跃迁。

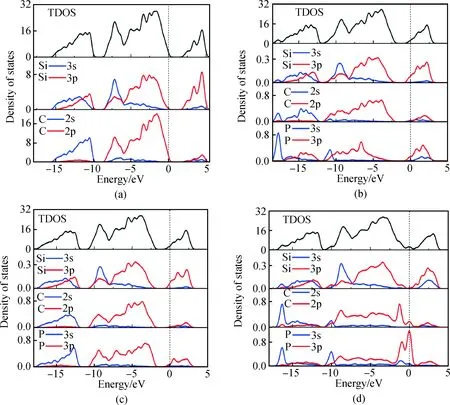
图4 掺杂前后6H-SiC的态密度:(a)未掺杂；(b)P替换Si；(c)P替换C；(d)P间隙掺杂Fig.4 Density of states diagram of 6H-SiC: (a) intrinsic (b) P substituting Si (c) P substituting C (d) P interstitial doping

2.3 光学性质

2.3.1 复介电函数

图5为掺杂前后6H-SiC的介电函数实部ε1(a)与虚部ε2(b)随入射光子能量的变化而不断变化的关系图，由图5(a)得出未掺杂6H-SiC在光子能量零点的介电函数ε1值为5.38，随后不断增大在5.3 eV处取得峰值12.1；P替换Si掺杂在能量零点的介电函数ε1值为6.6，在5.4 eV处取得峰值12，峰值变化较小；P替换C在能量零点的介电函数ε1值为7.32，在5.2 eV处取得峰值11.8；P间隙掺杂在光子能量零点的介电函数ε1值为6.7，峰值下降较明显，在5.1 eV处取得峰值10.8。通过掺杂介电函数ε1在零点的值明显增大。从5(b)得出未掺杂的6H-SiC在光子能为6.71 eV处取得介电函数峰值15.7，这归因于价带顶C 2p向导带低Si 3p电子跃迁所致。引入杂质P后强峰稍有下降且偏移，偏移是由P掺入后提供电子，游离电子极化引起，峰值变化是由价带顶C 2p向导带低Si 3p电子跃迁以及C 2p与Si 3p到费米能级P 3p电子跃迁所致[23]。掺杂后6H-SiC的介电函数虚部在低能区显著强于未掺杂的。掺杂后实部与虚部得到大幅度提升，结果表明掺杂对材料的光学参数影响较大。

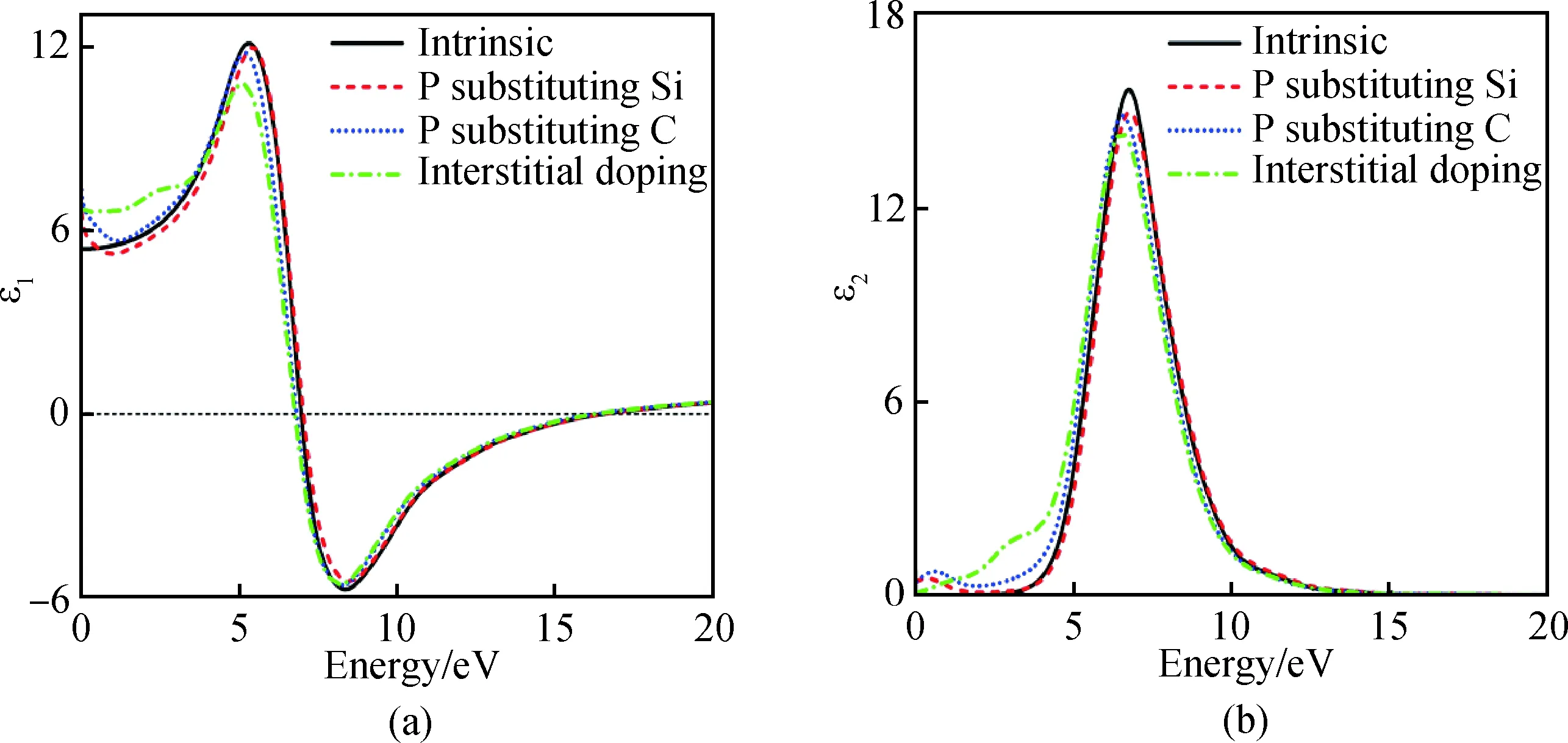
图5 掺杂前后6H-SiC介电函数实部ε1(a)与虚部ε2(b)Fig.5 Real part ε1(a) and imaginary part ε2(b) of the 6H-SiC dielectric function before and after doping

2.3.2 吸收光谱与反射谱

图6为掺杂前后6H-SiC的吸收光谱随能量变化的关系图，未掺杂的6H-SiC在能量小于2.4 eV以下不吸收光子，随着光子能量的增大在8.25 eV处取得最大吸收系数3.61×105cm-1，之后随着光子能量增加逐渐减小直至0。P替换Si、C与P间隙掺杂后均使得6H-SiC在小于2.4 eV以下吸收光子。P替换Si掺杂吸收峰与未掺杂吸收峰几乎重合；P替换C掺杂与P间隙掺杂吸收峰值略有下降。掺杂后在大于2.4 eV以上与未掺杂的吸收光谱变化趋势相似。

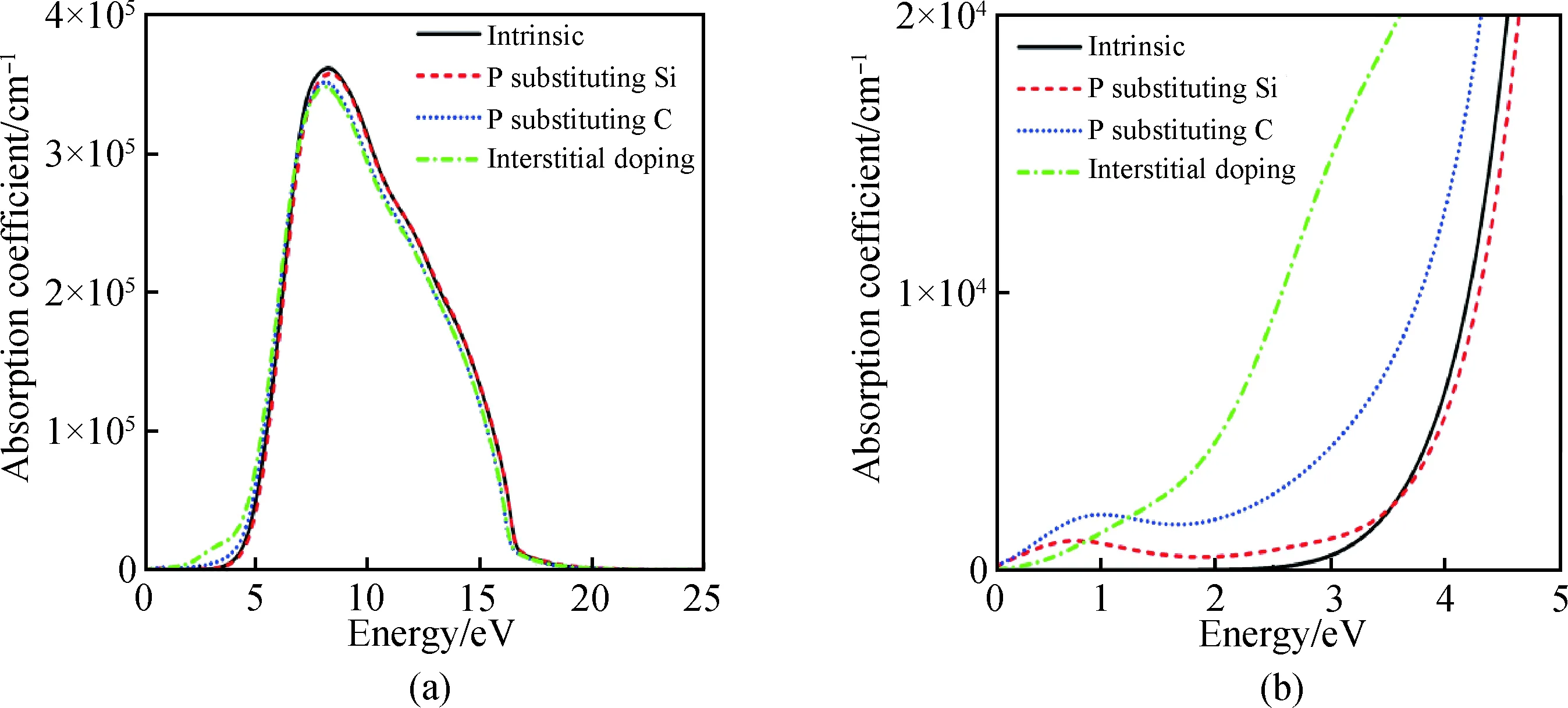
图6 掺杂前后6H-SiC的吸收光谱Fig.6 Absorption spectra of 6H-SiC before and after doping

图7(a)为掺杂前后6H-SiC的反射谱随能量增大而不断变化的关系图，掺杂前后6H-SiC的反射谱图在可见光与紫外光区变化不大，未掺杂的6H-SiC在15 eV处取得最大值，掺杂后的6H-SiC反射谱峰值略有减小。P替换Si、C以及P间隙掺杂6H-SiC反射谱出现红移现象，P间隙掺杂效果最佳。

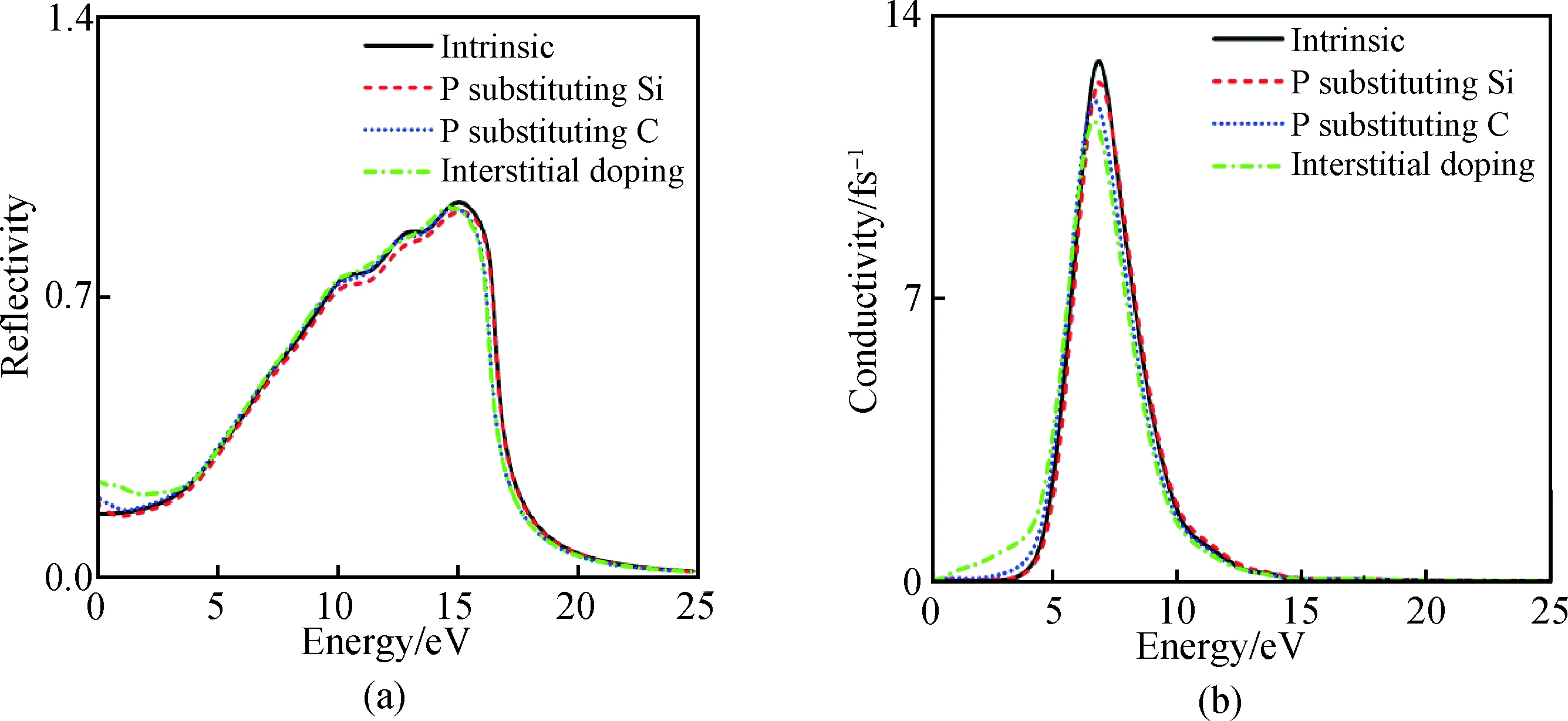
图7 掺杂前后6H-SiC的反射谱(a)与光电导率实部(b)Fig.7 Reflectance spectra (a) and real part of photoconductivity (b) of 6H-SiC before and after doping

2.3.3 光电导率

图7(b)为掺杂前后6H-SiC的光电导率实部与光子能量的关系变化图。未掺杂的6H-SiC在能量小于2.2 eV以下光电导率为0，在2.2 eV以上随着光子能量的增加光电导率单调递增，在6.85 eV光子能处取得光电导率最大值12.9 fs-1，达到峰值后随着光子能量增大光电导率单调递减。P替换Si、C以及P间隙掺杂后光电导率峰值有所下降，在低能区发生红移现象，在小于2.2 eV以下光电导率增强，其中间隙掺杂效果较明显。掺杂前后整体趋势在高能区变化不大。

3 结 论

基于密度泛函理论的赝势平面波法，计算并分析了未掺杂以及P替换Si、C以及P间隙掺杂6H-SiC的电子结构与光学性质，结果如下：

(1)未掺杂的6H-SiC是带隙为2.052 eV的间接带隙半导体，价带主要由Si 3s、3p与C 2p态电子共同作用形成，导带占主导的是Si 3p态电子，P替换Si、C掺杂带隙减小，分别为1.787 eV和1.446 eV；态密度向低能级偏移；费米能级插入导带，P替换Si、C掺杂呈n型掺杂。P间隙掺杂6H-SiC后电子结构变化最大，能带整体向下移动但部分价带向导带移动并跨入导带，带隙减小幅度较大为0.075 eV，P间隙掺杂呈p型掺杂。

(2) 未掺杂的6H-SiC在0 eV处的介电函数ε1值为5.38，P替换Si、C以及间隙掺杂6H-SiC在0 eV处的介电函数ε1分别为6.6、7.32和6.7，掺杂使得ε1显著增大。P替换Si、C以及间隙掺杂6H-SiC后ε2峰值有所下降，在低能区发生红移。未掺杂6H-SiC在2.4 eV以下不吸收光子，且在2.2 eV以下光电导率为0，掺杂P后6H-SiC的吸收光谱在0～2.4 eV范围吸收光子，光电导率在0～2.2 eV不为零，且反射谱在低能区均强于未掺杂。P替换Si、C以及间隙掺杂后6H-SiC在低能区的光学性能均强于未掺杂的，且P间隙掺杂在低能区的光学性能优于P替换掺杂，表明掺杂提高了6H-SiC对红外波段的利用。此次计算结果可为6H-SiC在红外光电领域提供有效理论依据。