两种不同地下洞室结构形式的动力响应分析与比较

黄丽静 安笑静 任亚丽

（军事科学院国防工程研究院，北京 100036）

0 引言

随着我国石油战略储备项目的实施，大跨度直墙拱形洞室与穹顶洞室均有所应用。目前，国内外研究机构和专家学者对于直墙拱形洞室的围岩稳定性、破坏机理及加固措施问题进行了大量的研究，取得了丰富的研究成果[1-5]，例如朱维申对典型的直墙拱洞室群在不同条件和多因素影响下高边墙位移规律的预测进行了研究[1-2]；顾金才院士通过模型试验，系统研究了最大初始开洞荷载与洞室轴线平行作用下直墙拱顶试验的破坏形态和机理[3]；高延法经过对比试验设计了直墙半圆拱形钢管混凝土支架[4-5]。但是对于地下油料储库中经常使用的大跨度穹顶结构的设计计算问题，特别是国防工程中所需要的爆炸荷载作用下的理论分析涉及较少。

本文通过数值分析，研究了深埋穹顶洞室结构与直墙拱洞室结构在爆炸荷载作用下的动力响应，并将这两种结构破坏时的变形及破坏模式进行分析对比，认为穹顶结构抗爆能力具有明显优势，并类比了同跨度下的两种地下洞室结构的破坏荷载，可为地下工程设计特别是穹顶结构工程设计提供理论分析参考。

1 数值分析模型的建立

1.1 直墙拱结构有限元模型及边界设置

直墙拱结构由于结构界面对称，取1/2 截面建立计算模型，侧向与底部的边界长度取5 倍以上结构最大尺寸。左右两侧为水平约束，约束该边界相应方向的位移，模型边界上添加透射边界，计算简图如图1所示。采用单点积分的四节点平面实体单元进行离散，经过网格敏感性分析，单元大小取为0.25 m×0.25 m，整个模型共划分单元589739 个。

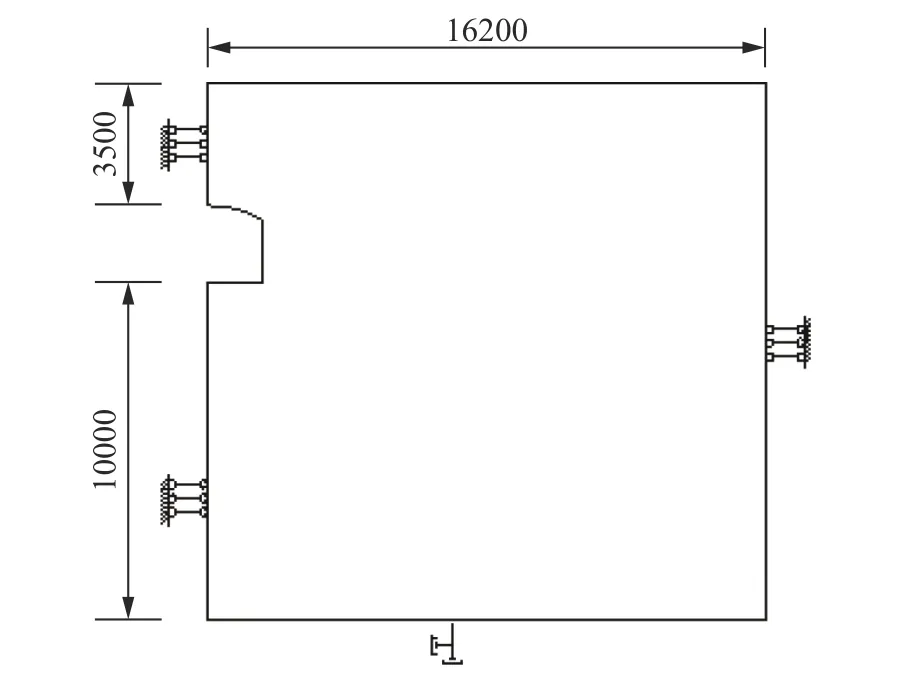
图1 有限元计算模型（单位：cm）

1.2 材料模型及参数

围岩简化为各向同性均匀介质，采用LS-DYNA中MOHR_COULOMB 弹塑性模型进行描述。根据摩尔-库伦准则[6]（见图2），对于岩石等脆性材料其剪切强度表示为

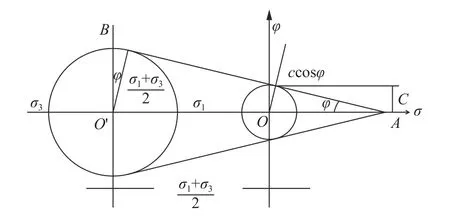
图2 摩尔-库伦破坏准则示意图

因此，当σ1·tan2φ-σ3≥σc则岩石破坏。

LS-DYNA 中的MOHR_COULOMB 模型是一种理想弹塑性模型，根据相关文献，围岩计算参数取值如表1所示[7]。

表1 岩体物理力学指标

1.3 穹顶洞室的有限元模型及边界设置

考虑结构的轴对称性，可以建立穹顶洞室结构的轴对称分析模型[8-9]，其模型边界设置方法、材料参数以及数值计算方案与直墙拱结构相同。

2 两种结构破坏形式及分析单元的选取

2.1 直墙拱结构

图3 为Ш级围岩不同跨度洞室在爆炸荷载作用下的破坏范围分布图。当满足最小安全防护层厚度35 m 埋深时，各个洞室在核荷载作用下的破坏形式相同均为侧墙出现楔形破坏，且楔体内部塑性应变均比较小，并没有达到所定义的破坏塑性应变，没有发生破坏。文献[10]通过大量模型实验指出在地面空气冲击波荷载作用下，坑道的整体破坏发生在两侧边墙上，对于毛洞则首先在洞壁两侧产生楔形滑移。楔体内部材料比较完整，没有破坏裂缝，其破坏形态和静力条件下室内模型试验结果极其相似。文献[11]通过模型试验指出，直墙拱结构在静载作用下，侧墙先于拱顶发生破坏，并指出侧墙的破坏形式为剪切破坏。直墙拱结构在核荷载作用下的破坏形态和文献[10]、文献[12]的模型试验结果一致，其破坏形态与静力作用下的直墙拱相同。

图3 35 m 埋深下不同跨度直墙拱洞室的破坏范围分布图

为分析两种不同洞室结构发生上述破坏的机理，选如图4所示的单元，单元编号从左往右分别为B-I，从上往下分别选5 组，编号为①-⑤。分别分析单元中X、Y、XY 方向的应力以及X、Y、XY 方向的应变，根据应力及应变对照结构的破坏面分析结构的破坏机理。

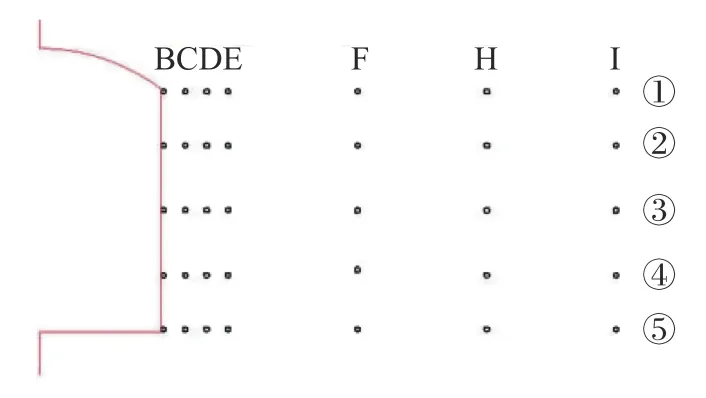
图4 选取单元位置示意图

2.2 穹顶结构

图5 为Ш级围岩不同跨度洞室的破坏范围分布图。从图中可以看到35 m 埋深下，各个洞室的破坏形式相同。由塑形应变最大图可以看出，破坏位置出现在拱顶、拱脚、以及侧墙临空面上。在拱顶及拱脚处，其剪切破坏面并没有继续扩展，在底板处也会有较大的塑性应变。文献[13]指出在较大的平行于轴线方向的压力作用下，侧墙会出现一层层片状的所谓

图5 35 m 埋深下不同跨度穹顶洞室的破坏范围分布图

“应力剥落”现象，洞室发生受压破坏。从破坏图可以看出在侧墙内部未形成类似直墙拱结构的典型楔形破坏，而是沿侧墙临空面发生了上下贯通的破坏，其破坏面与洞室的轴线平行。

为进一步分析穹顶结构破坏机理，选取图4所示的单元，同时与直墙拱洞室结构进行参数性一致对比分析。

3 直墙拱结构与穹顶结构的对比分析

3.1 变形的能力

图6 为穹顶结构洞室与直墙拱室在不同荷载作用下的最大变形对比。由图6（a）可知，直墙拱结构洞墙中水平位移明显比穹顶结构洞室的大。随着荷载的增大，直墙拱结构洞墙中水平位移最大值随跨度由线性变化到呈加速增大趋势，而穹顶结构洞室墙中水平位移最大值随跨度更接近线性变化。直墙拱结构洞墙中水平位移是穹顶结构洞室的2.0～5.7 倍。从图6（b）可以看出，底板与墙底最大变形在同样荷载下和跨度基本呈线性关系，直墙拱结构底板最大变形与穹顶结构洞室几乎相等。从图6（c）可以看出拱顶变形最大值随着跨度的增大而增大，直墙拱结构洞室拱顶变形是穹顶结构洞室的1.7 倍。说明穹顶结构其整体变形较好，穹顶结构的水平与竖向变形比例比直墙拱结构的更加均匀。

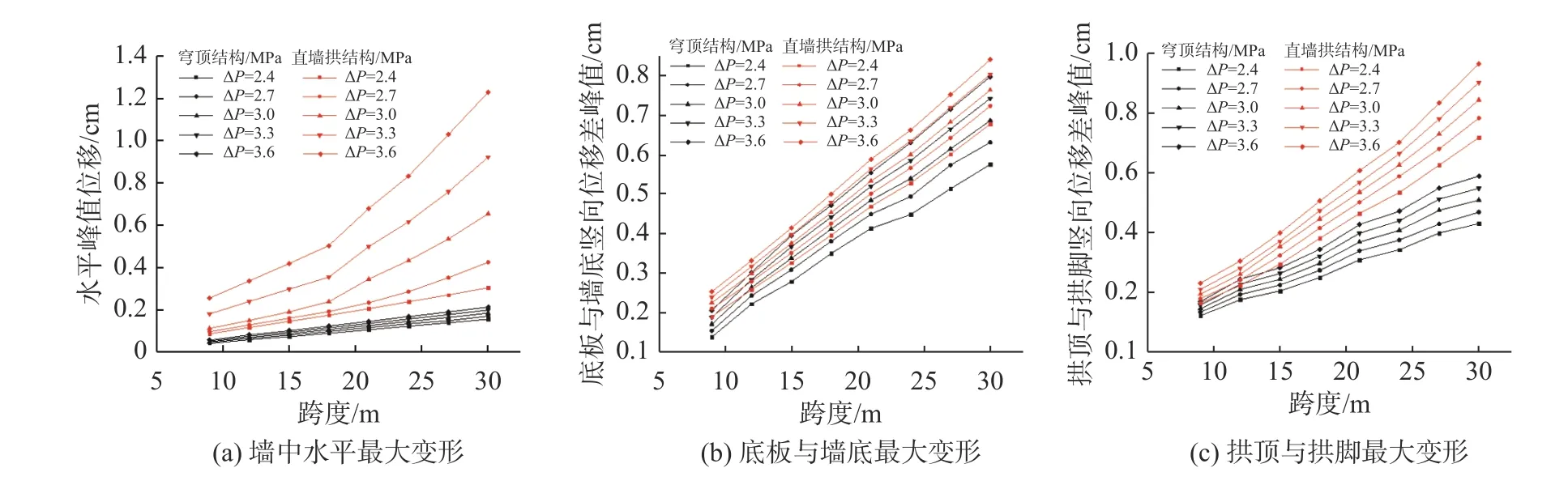
图6 洞室最大变形对比图

3.2 破坏荷载的比较

当M-C 材料模型的塑性应变达到1.27×10-3时，可认为材料发生破坏[14]。通过数值对比（见图3、图5）可以看到，穹顶结构所能承受的极限荷载随跨度增大而减小，9 m 跨度穹顶结构的破坏荷载为6.6 MPa，30 m 跨度时破坏荷载为6.3 MPa，可以看出穹顶结构其破坏荷载随跨度减小的幅度并不大，仅减小了4.6%。与之对比的直墙拱结构其破坏荷载随跨度呈线性减小，9 m 跨度直墙拱结构的破坏荷载为3.9 MPa，30 m 跨度时破坏荷载为3.3 MPa，减小的幅度为15.4%。可见穹顶结构的抗爆能力明显优于直墙拱结构。特别对于大跨度结构，穹顶结构的优势比较明显[15]。例如9 m 跨度时，穹顶结构的抗爆能力是直墙拱结构的1.69 倍；30 m 跨度时，穹顶结构的抗爆能力是直墙拱结构的1.91 倍（见图7）。

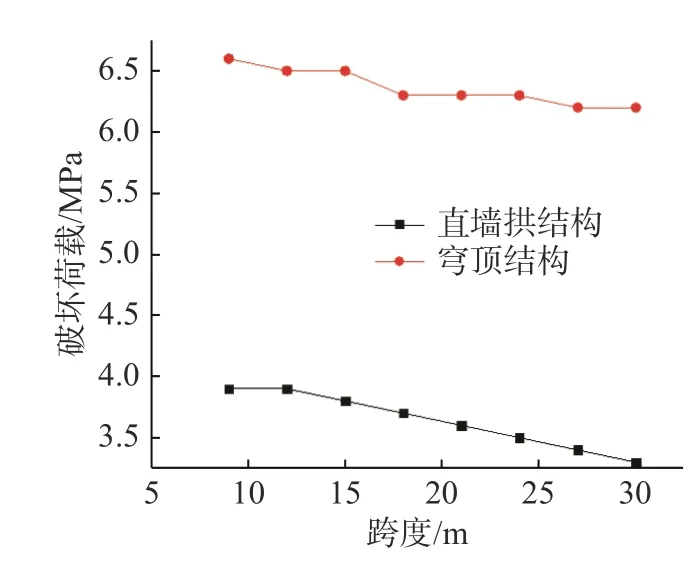
图7 破坏荷载比较

3.3 破坏模式的比较

为比较穹顶结构与直墙拱结构的破坏机理，分析两种结构的洞室周围应力，选如图4所示的单元，分别分析单元X、Y、XY 方向的应力，比较两种结构在同一荷载（3.6 MPa）作用下的应力分布情况，进一步分析两种结构的破坏机理。从之前的两种结构的破坏图，可知①和⑤、②和④的应力应变及破坏形式相同，故只需分析①、②、③组单元的应力即可说明洞室侧墙整个应力分布状态。

图8 为第一组单元的应力峰值随距离变化关系。从图中可以看出，直墙拱结构的X、Y、XY 应力峰值均比穹顶结构大，且两种结构的应力变化趋势相同，在第一组的B 单元，两者的破坏均为压剪破坏。

图8 第一组单元的应力应变时程曲线

图9 为第二组单元的应力峰值随距离变化关系。从图中可以看出，直墙拱结构的X、Y、XY 应力峰值均比穹顶结构大，且两种结构的应力变化趋势相同，直墙拱结构在侧墙一定深度处（C 单元）压应力和剪应力都急剧增大，因而侧墙先发生压剪破坏，由于3.6 MPa 作用下，穹顶结构还处于弹性状态，因此单元并没有发生破坏，从穹顶结构应力峰值随距离变化的统计值可以看出，在一定深度处，压应力及剪应力也将加大，但是从压应力和剪应力的应力数值大小可以看出，剪应力远远小于压应力，最大仅为压应力的1/10，而在侧墙临空面其压应力值较大，因此穹顶结构会先发生受压破坏。

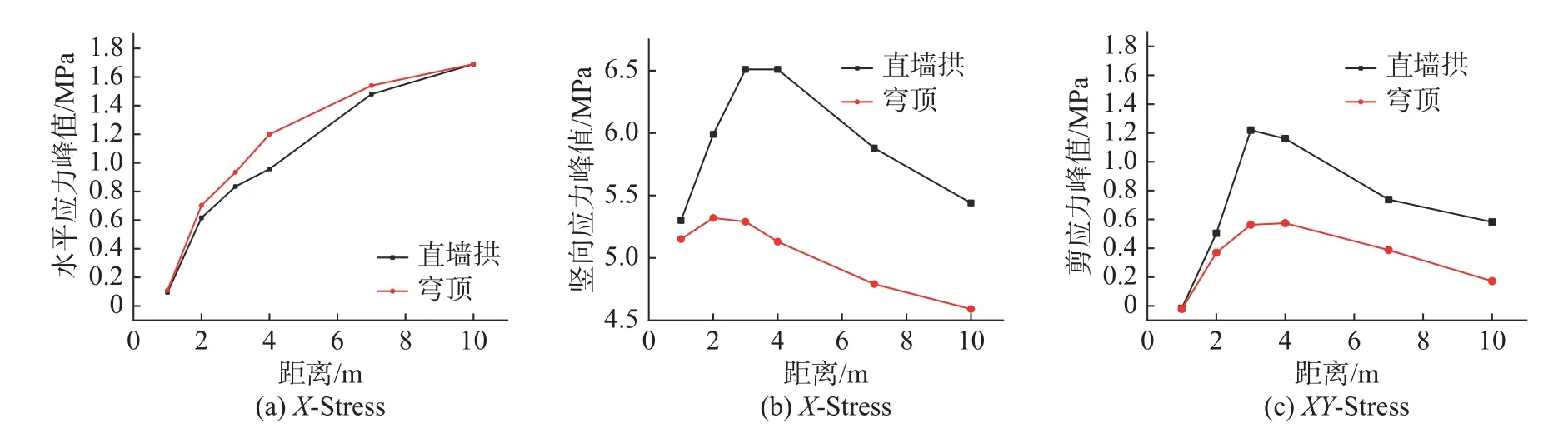
图9 第二组单元的应力应变时程曲线

图10 为第三组单元的应力峰值随距离变化关系。结构的X、Y、XY 应力峰值均比穹顶结构大，且两种结构的应力变化趋势相同，直墙拱结构在侧墙一定深度处（D 单元）压应力和剪应力都急剧增大，因而侧墙先发生压剪破坏，由于3.6 MPa 作用下，穹顶结构还处于弹性状态，因此单元并没有发生破坏，从穹顶结构应力峰值随距离变化的统计值可以看出，在一定深度处，压应力及剪应力也将加大，但是从压应力和剪应力的应力数值大小可以看出，剪应力远远小于压应力，最大仅为压应力的1/10，而在侧墙临空面其压应力值较大，因此穹顶结构会先发生受压破坏。

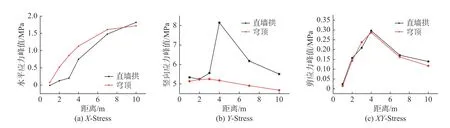
图10 第三组单元的应力应变时程曲线

综上所述，直墙拱和穹顶结构在侧墙位置随距离的变化，应力峰值变化的趋势一样，且一定深度处压应力和剪应力都增大，直墙拱结构破坏的原因是拱顶没有穹顶结构的边界约束强，故侧墙先发生剪切破坏，而穹顶结构的边界约束强，侧墙先发生受压破坏。

4 结论

本文通过数值模拟，分析了深埋穹顶洞室结构与直墙拱洞室结构在爆炸荷载作用下的动力响应，并将这两种结构破坏时的变形及破坏模式进行分析对比，基本结论如下：

(1)穹顶结构在同一荷载作用下，洞室的变形随跨度的增加而近似呈线性增加。随着荷载峰值的增大，洞室变形随跨度增大的幅度增大，穹顶结构的整体变形能力要优于直墙拱结构。

(2)穹顶结构的破坏荷载随跨度并近似呈线性关系，且远比直墙拱的破坏荷载大；9 m 跨度穹顶结构的破坏荷载为6.6 MPa，30 m 跨度时破坏荷载为6.3 MPa，穹顶结构的承载能力明显优于直墙拱结构，跨度增大时穹顶结构的优势更加明显，9 m 跨度时穹顶结构的承载能力是直墙拱结构的1.69 倍，30 m 跨度时为1.91 倍。

(3)分析了洞室周围应力应变的变化规律，表明穹顶结构在爆炸荷载作用下的破坏主要是侧墙受压破坏，在拱脚及墙脚应力集中的地方发生压剪破坏。