基于多层LSTM的复杂系统剩余寿命智能预测

2022-02-21王华伟

兵器装备工程学报 2022年1期

付强，王华伟

(南京航空航天大学民航学院，南京 211106)

1 引言

预测剩余寿命(remaining useful life，RUL)作为复杂系统健康管理的关键内容之一，由于系统结构复杂与故障耦合以及内、外部因素共同作用导致性能退化，预测方法存在不准确性。考虑到噪声与模型参数配置的影响，She等[1]提出了一种基于自举双向门控递归的预测方法并分析其不确定性，通过ABLT-1A轴承数据证明了该方法的有效性。针对目前电池剩余寿命预测模型存在模型兼容性较差的问题与模型性能受健康因子精度的影响，庞晓琼等[2]设计一种基于非线性自回归网络的寿命间接预测方法，其实验结果表明在同型号不同电池的寿命预测中所提方法具有一定优势。Zhou等[3]对基于混合遗传算法的电容器剩余寿命预测模型进行鲁棒性评估，在一定均方根误差范围内，利用在线训练与离线历史数据实现了高精度预测。

传统机器学习与统计学等手段在复杂系统剩余寿命预测方面取得了一定的成果，但这些方法的性能较为依赖提取到的数据特征及其质量。深度学习具有非线性表征能力强与不依赖高质量特征的优势。循环神经网络(recurrent neural networks，RNN)作为一种针对时序数据预测的经典深度学习模型，其广范应用在复杂系统的剩余寿命估计中[4]。Yu等[5]为估算机械系统的剩余寿命，提出了一种基于RNN的相似度退化轨迹匹配方法。Rivas等[6]设计一种基于RNN的复杂系统预测性维修模型，并利用准确率、召回率与F1分数评价模型性能。

尽管RNN模型提高了时序数据处理的能力，但由于梯度消失与爆炸等问题，其无法捕获长期依赖关系。长期短期记忆(long short term memory，LSTM)模型是作为一种改进的RNN模型弥补了RNN的不足[7]。LSTM利用选通机制提高了性能，能够控制进入模型的信息量和在存储器中的过去信息。黄承赓[8]提出一种基于LSTM的产品剩余寿命预测方法，具有对时序数据的建模优势与极强的非线性建模能力。Li等[9]考虑到人为因素对电池系统的影响，研究一种基于LSTM的故障时间预测并对潜在故障进行风险评估，能够准确预警故障。Ding等[10]提出一种基于多阶迭代LSTM的轴承剩余寿命预测模型，并优化模型超参数，实现了早期预警。Wang等[11]通过传感器收集了阀门状态数据，利用LSTM进行特征提取与寿命预测，以进一步提高核电系统的维护效率。Yan等[12]提出了一种基于有序神经元LSTM的齿轮剩余寿命预测模型，研究显示所提方法相比于RNN模型收敛速度更快，实现了最佳精度的短期与长期预测，并且具有良好的鲁棒性。航空发动机作为一种复杂、精密的系统，准确地估计其剩余寿命，能够提前采取适当的维护措施，以避免灾难性故障并最小化经济损失。Yuan等[13]利用LSTM在复杂操作、混合故障与强噪声情况下实现准确预测航空发动机寿命。

在基于深度学习的复杂系统剩余寿命预测的基础上，提出一种改进的多层LSTM预测模型，其能够避免梯度消失，引入Dropout方法避免过拟合，深度挖掘多尺度时序数据特征，解决复杂系统变工况条件下预测准确性不足问题，并且全面地、标准地评估预测模型性能。

2 基于多层LSTM的RUL预测

针对复杂系统，从海量监测数据中充分挖掘出有价值的性能退化信息，并准确地建立相应的RUL预测模型，当前需求迫切。基于多层LSTM的预测模型能够自主推断隐藏在时序数据中的因果关系，并通过训练学习直接获取退化特征。因此多层LSTM能够处理高维度、多尺度时序数据，提供准确RUL预测结果。

2.1 多层LSTM网络结构

在实际工程背景下，单层LSTM网络难以满足复杂系统在不同工况下的剩余寿命预测。将前一层LSTM网络的输出，作为后一层LSTM网络的输入，以建立多层LSTM网络。堆叠多层LSTM网络以保证其能够提取不同工况下时序数据的深层次抽象特征，并且增加模型的非线性拟合能力与模型稳健性。LSTM网络的层数与各层神经元节点数量均为超参数，需要在预测试验前初始化设置。利用网格搜索方法并结合交叉验证算法以确定最优的超参数，多层LSTM网络结构如图1所示。

图1 多层LSTM网络结构框图

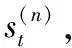
(1)

(2)

(3)

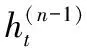
(4)

式(4)中，Relu(x)=max(0，x)。

2.2 基于Dropout的多层LSTM模型改进

过拟合是多层LSTM模型存在的重要问题之一。多层LSTM模型训练与学习的本质上是优化与泛化。调试多层LSTM模型参数，在训练样本集中将损失函数值降至最低。充分训练后的预测模型在测试样本集中的性能反映出模型泛化能力。过拟合能够影响训练模型性能进而降低泛化能力。

为了防止多层LSTM神经网络等模型过拟合训练样本集，采取正则化技术来限定模型的复杂度。在目标函数中增加模型参数的正则化项。Dropout方法则是针对深度学习最有效的正则化手段之一，标准网络与基于Dropout的网络如图2所示。

图2 标准网络与Dropout网络示意图

训练过程中对某一层网络使用Dropout，随机使其中某些神经元节点以一定的概率停止激活。弃用一些隐含层神经元节点，减少了神经元之间的固定耦合性，并且筛选出的节点能够与其他节点配合。因此引入Dropout后的多层LSTM不会过分依赖于某些特征，避免了过拟合，使得泛化能力更高。

2.3 基于误差得分函数的预测模型评估

误差得分函数具有评估预测不对称性的功能，满足早期与后期预测，超前与滞后预测的评估需求。设滞后与超前参数分别为α1与α2，误差得分函数为：

(5)

式(5)中：s为误差得分；n为测试点数量；d为误差值。

针对复杂系统安全运行，避免严重性故障，特别是在运行后期中与滞后预测相比，旨在较为保守的超前预测RUL，如图3所示。但是，在某些情况下，故障可能不会造成严重性后果，因此超前预测可能会导致不必要的维修费用与停机损失。因此应合理设计超前与滞后参数，得分函数的不对称性随之也发生变化，以满足特定要求。

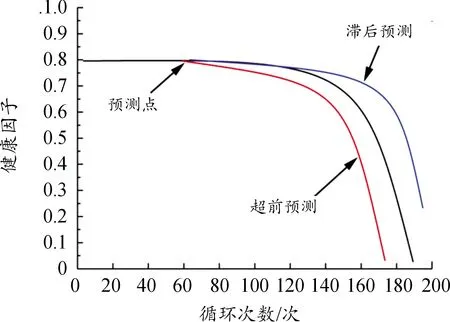
图3 超前预测与滞后预测曲线

图4为不同误差得分情况下评估预测模型性能函数曲线。在案例1和案例2中，参数α1与α2分别相等，所以超前与滞后评估优先级是对称的，都随着误差呈指数增加。在案例3中，如果时间序列的长度较短，则应为指数项设置较高值；相反，当时间序列相对较长时，配置较高值，以提高评估性能。案例4显示了超前与滞后预测不对称的情况，滞后预测得到了更多的误差惩罚。但是，如案例5所示，超前预测可能需要考虑不必要的维护成本。

图4 不同误差得分情况下的评估预测模型性能函数曲线

预测评估方法为RUL估计模型提供了准确验证与模型性能评估。特别是在多工况复杂系统中，利用误差得分函数能够有效评估超前与滞后预测，并初始化不同的参数以满足各种预测评估需求。

3 算例分析

航空发动机为一种典型的复杂系统，以航空发动机为例验证本文提出方法的有效性。从航空发动机运行过程中采集原始监测数据，数据未经任何处理或清洗，如图5所示。数据源于NASA研发的数据采集系统C-MAPSS[14]。部分参数随着循环次数的增加变化明显，但从整体数据来看，数据特征质量低。

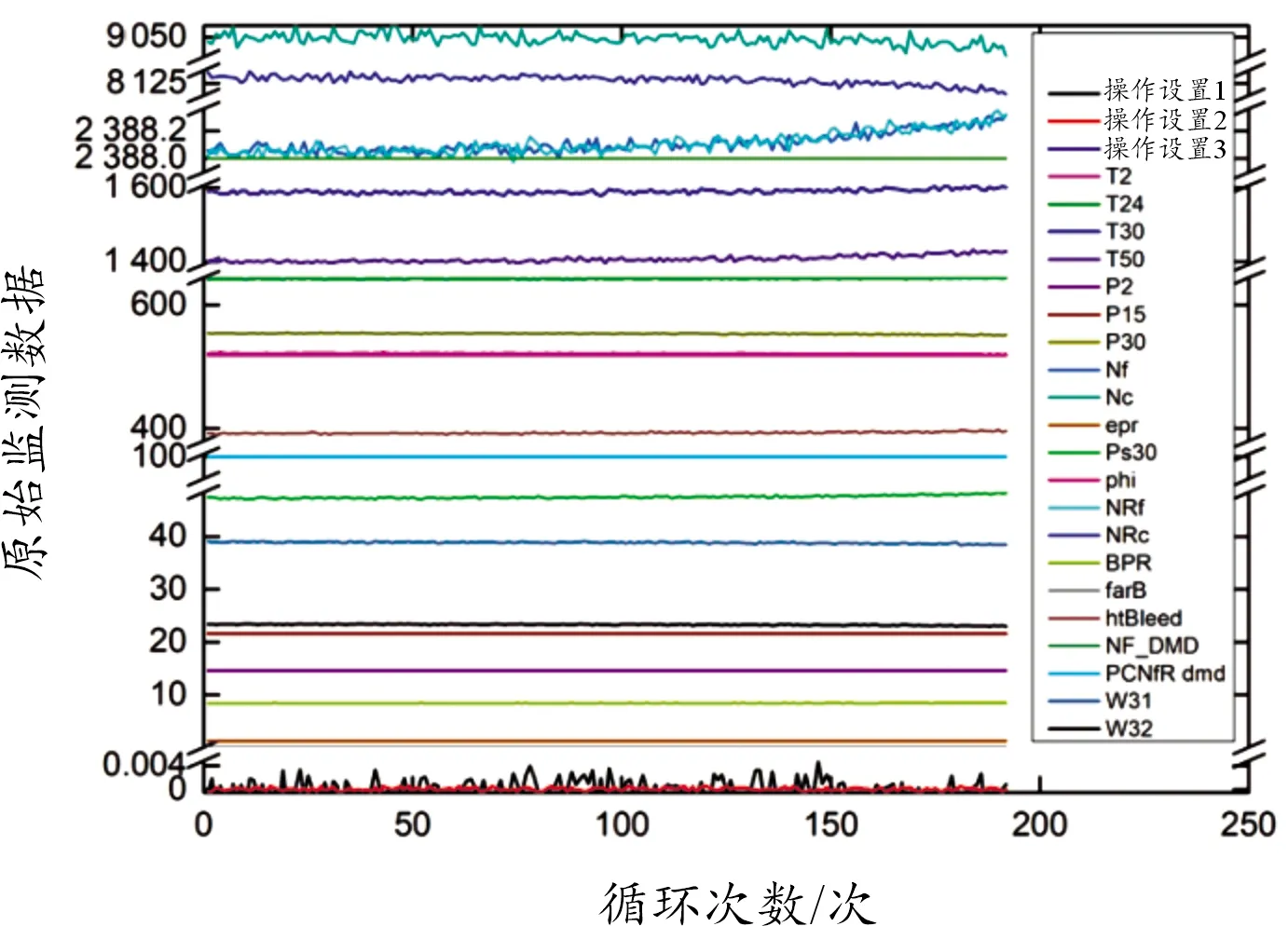
图5 原始监测数据曲线

为了避免在基于数据驱动的复杂系统健康管理中出现过拟合与欠拟合，将采集的原始监测数据集互斥分割为训练集、验证集与测试集，同时能够为航空发动机健康管理数据与智能模型的交互学习提供支撑。训练集为航空发动机从初始状态到故障阈值的退化状态数据。验证集的功能为检测经过反复训练后健康管理模型的泛化能力，将检测结果反馈至模型，基于需求调节健康管理模型中的超参数以获取更高的泛化能力。在实际航空发动机健康管理场景下，验证集保证了训练好的模型其性能测试效果最佳。测试集的功能为评估最终智能健康管理模型的泛化能力以及模型性能。

3.1 航空发动机工况分析

航空发动机性能退化过程中，操作设置为高度，马赫数与温度。操作设置、外界环境、系统负载等因素都会对运行工况产生影响，并且运行工况随时间变化，增加了RUL预测不确定性。

针对复杂工况下航空发动机性能退化，利用K-means方法识别当前特定运行工况，经过模型参数调试，聚类中心参数为6时，即6种运行工况，聚类效果最好，如图6所示。

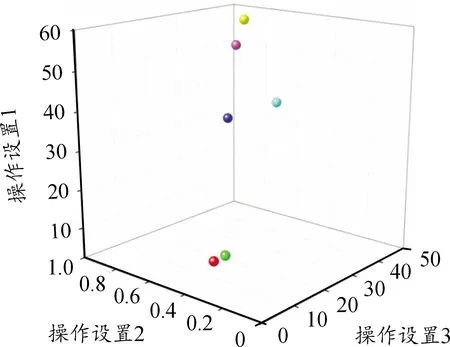
图6 航空发动机运行工况识别图

K-means方法特点为类内距离小，类间距离明显，能够对将航空发动机运行工况有效地聚类与识别。

在原始数据集中，对某台航空发动机进行工况识别，如图7所示，航空发动机在30次循环中，工况转换频率高。分析航空发动机工况，为变工况条件下RUL预测提供了支撑。

3.2 建立航空发动机健康因子

考虑到航空发动机在运行初期其性能处于健康状态，故障率稳定并且较低。在运行后期阶段，健康状况持续下降，故障率随着时间的增加而急速递增，最终达到严重故障状态，如图8所示。潜在故障点是稳定区域到功能故障的过渡。稳定区域是航空发动机初始运行到潜在故障点的时间。基于状态监测数据的健康因子超过潜在故障点时，航空发动机系统进入退化区域，并且会以一定速率向功能故障转化。根据稳定与退化区域以及故障点位置，在航空发动机开始急速衰退之前采集的监测数据，不宜用于RUL预测模型的训练。

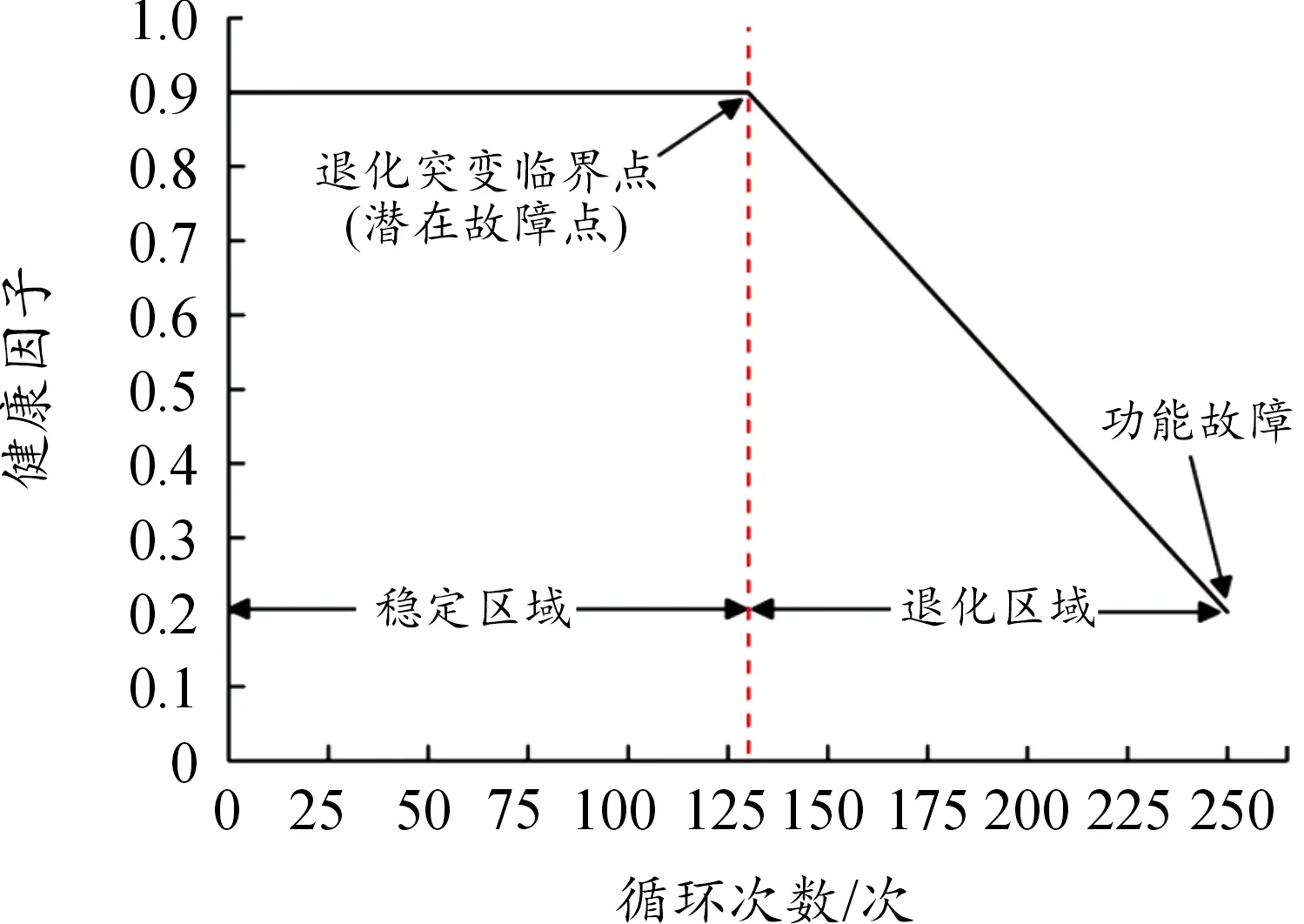
图8 航空发动机退化模型的健康状态曲线

建立高维监测参数与航空发动机退化状态的映射关系，利用健康因子定量描述健康状态，将航空发动机14个关键参数利用主层分分析(principal component analysis，PCA)进行多维数据融合。各成分方差如表1所示。

表1 各成分方差

总方差百分比如图9所示。选择方差最大的主成分数据，即主成分1数据，以建立航空发动机健康因子。

图9 各主成分方差占总方差的百分比直方图

主成分1是原14维航空发动机监测参数的线性组合，其变换系数如表2所示。主成分1的变换系数与航空发动机各个参数退化趋势相符合，这也证明了选择主成分1的合理性。

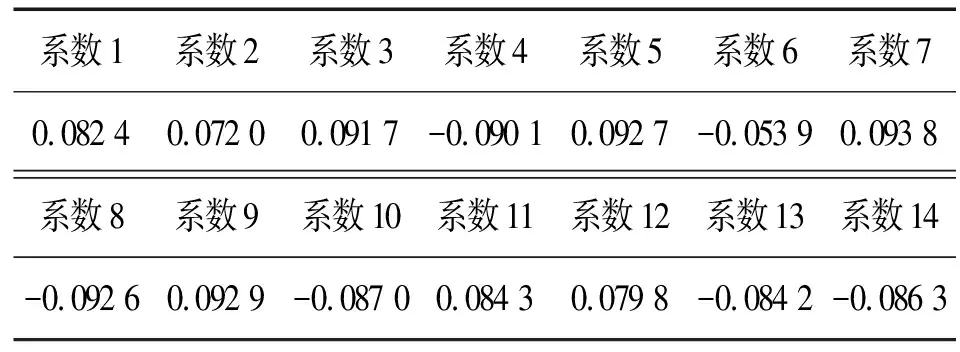
表2 主成分1的线性变换系数

根据主层分1的变换系数进行多维度数据融合，以构建健康因子，如图10所示。

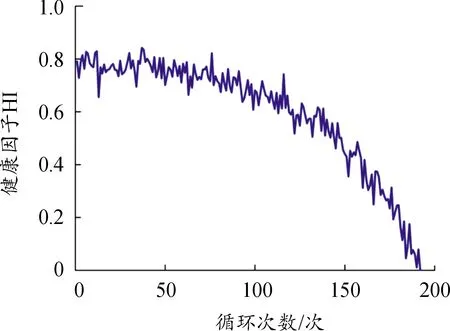
图10 航空发动机健康因子退化曲线

在图10中，航空发动机运行状态下，多种传感器采集大量监测数据，包含了大量测量误差与噪声。RUL预测模型在训练阶段，神经网络存在从噪声中学习的可能。

为减少数据不确定因素的影响，对健康因子退化曲线进行平滑处理，以描述循环次数与健康因子之间的准确关系。基于高斯模型、指数模型、幂函数模型与傅立叶变换的健康因子曲线拟合结果如图11所示。

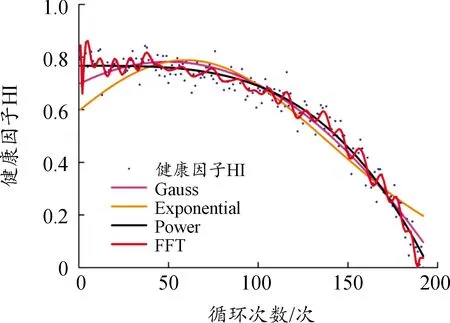
图11 健康因子拟合曲线

拟合曲线有利于确定随时间变化的退化程度，高斯模型、指数模型与傅立叶变换的拟合在航空发动机早期退化时，其拟合曲线变化趋势都不具有稳定性。基于幂函数模型的拟合在早期退化阶段具有稳定的退化趋势，且退化增量最小，拟合曲线没有任何其他波动趋势。从构建的健康因子退化曲线结果来看，基于数据融合的健康因子一方面能够全面表征航空发动机退化过程，保留原始退化模式；另一方面退化曲线单调性较好，曲线噪声较小。

3.3 多层LSTM模型配置

将航空发动机健康因子作为多层LSTM模型的输入，其输出为航空发动机的RUL估计值。堆叠式LSTM模型通过增加网络的深度，一方面能够处理航空发动机变工况，另一方面提高训练的效率，获得更高的准确性。为研究LSTM层数对RUL预测性能的影响，采用训练集与验证集对不同层数的LSTM模型进行对比试验。考虑到各个航空发动机初始退化状态均有差异，且故障模式与操作模式也各不相同，利用验证集交叉验证预测模型的准确性，最终根据RMSE结果选取RUL模型层数，试验结果如图12所示。

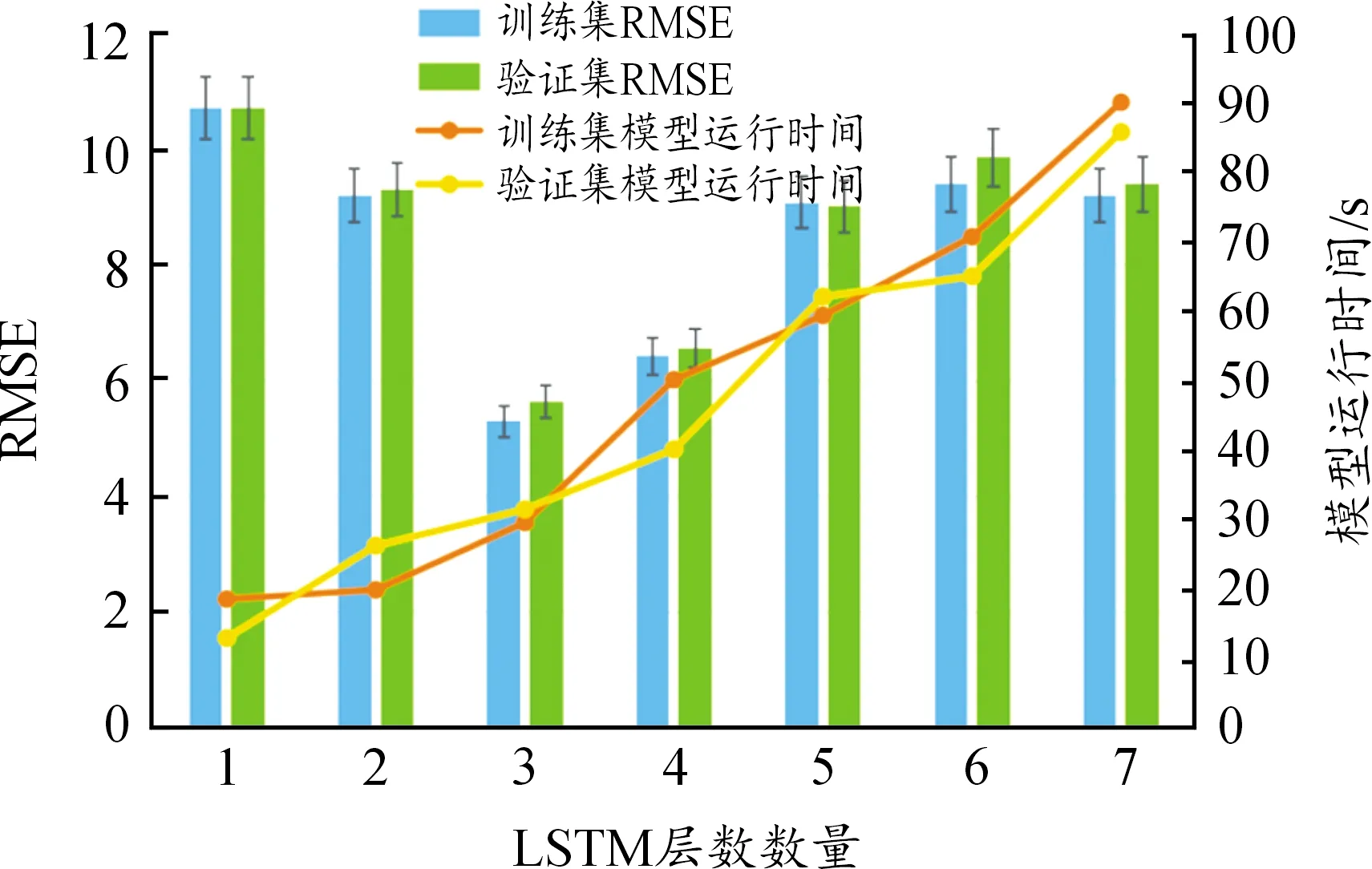
图12 多层LSTM模型不同层数的性能曲线

LSTM网络层数对航空发动机的RUL预测性能有着极大的影响。堆叠的LSTM层数越多，RMSE并不一定越小，其内在原因是LSTM的层数增加会导致运算时间与内存消耗的指数级增长，并且产生层与层之间的梯度消失。当LSTM的层数超过了3层，层与层之间的梯度消失情况会变得非常明显，网络训练更新迭代缓慢，收敛效果与计算效率急剧下降，甚至进入局部最小的情况。根据计算成本与模型容量，避免模型过拟合，最终确定多层LSTM模型的层数为3。

进一步分析多层LSTM模型性能，验证其有效性，对训练与验证损失值进行对比分析，并与RNN模型、单层LSTM模型相比较，以检测训练后的模型性能，其损失值曲线如图13所示。

在图13中，随着训练次数的增加，训练集与验证集的损失值逐渐减少，在收敛状态下多层LSTM模型的平均验证损失值为0.023，相比于单层LSTM模型，低了28%，相比于RNN，减少了40%。多层LSTM模型的验证方差相比于RNN模型与单层LSTM模型，分别降低了11%与53%，这也反映出多层LSTM模型更具稳健性。

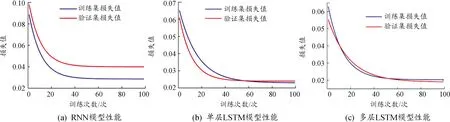
图13 训练后不同预测模型性能

在航空发动机RUL预测过程中，时间步长影响着模型预测效果。为分析时间步长大小对多层LSTM模型精度的影响，设计时间步长分别为5，10，15，20，25与30，进行RUL预测试验，结果如图14所示。

图14 不同时间步长的RMSE与运行时间曲线

图14给出了多层LSTM模型在不同时间步长的RMSE与模型运行时间的变化规律。随着时间步长的增加，多层LSTM模型能够提取健康退化特征越多，RUL预测误差越小，但是模型计算时间越长。当时间步长由5增加至10时，步长大小增加了50%，模型的RMSE降低了33%。当时间步长为20，25与30时，RMSE仅有微小变化而且下降幅度不明显。考虑到计算成本，多层LSTM的时间步长设置为20。

3.4 预测结果分析

充分训练的多层LSTM模型为健康因子与剩余寿命的映射关系提供了可能。将航空发动机测试集输入到训练好的模型中，将健康因子阈值设置为0.15，分别在第120次循环预测点A与第150次预测点B估计航空发动机的剩余寿命，预测结果如图15所示。对于预测点A，健康因子在第203次循环退化至阈值以下，A点RUL为83次循环，绝对误差为17个周期，属于滞后预测。同理，预测点B的RUL为29个周期，绝对误差为7个周期，属于超前预测。RUL预测绝对误差越小，证明RUL预测结果越好，正预测误差优于负预测误差，即超前预测优于滞后预测。

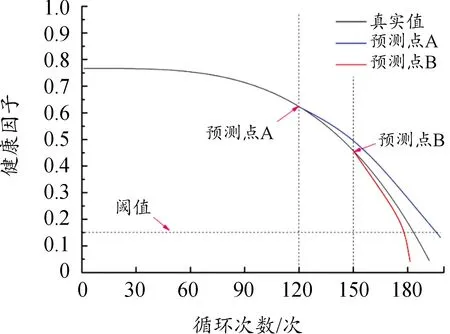
图15 航空发动机剩余寿命预测曲线

基于多层LSTM模型的寿命预测方法，能够从健康因序列中自适应地挖掘退化特征，进而有效地预测航空发动机RUL，特别是在航空发动机寿命的中后期，例如预测点B。

为证明多层LSTM模型的通用性与适用性，利用单层LSTM与RNN预测结果作对比试验。根据在预测点A与B的预测值，计算RUL的预测平均误差，如表3所示。与单层LSTM与RNN模型相比，多层LSTM平均预测误差为12，较单层LSTM与RNN分别降低33%与50%。对比试验结果表明，改进的多层LSTM具有较低误差水平。

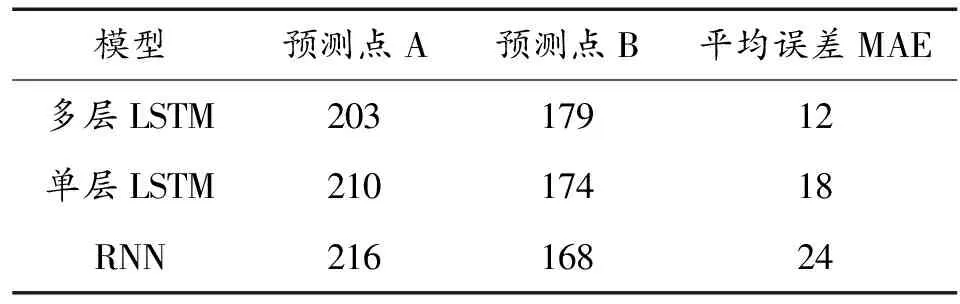
表3 不同预测点各种预测模型性能

RUL预测性能随着历史数据的增加而提高，但在基于较少历史数据的预测中，退化过程相关的时序数据存在有限性。考虑到噪声与其他操作设置引起的数据波动影响，预测较远的故障时间点时，时序预测结果具有不确定性。因此，有必要分析不同预测点的模型性能。在实际RUL预测场景中，更注重航空发动机中后期的预测结果及其精度。为了探究航空发动机在生命周期中各时段的预测性能，对测试集中的航空发动寿命数据分别从60%、70%、80%与90%处进行RUL预测。统计预测绝对误差分布情况，如图16所示。

图16 不同预测点的绝对误差曲线

图16给出了不同预测点的预测结果对比，改进的多层LSTM模型对于不同时段的RUL预测效果并不相同。当航空发动机在60%的历史数据处预测时，多层LSTM模型的绝对误差范围为(6，26)，当预测点为90%处时，绝对误差范围为(0，9)，预测绝对误差分布相对较为集中。当历史数据长度足够，并且航空发动机退化成熟到足以为RUL计算提供必要的信息时，预测性能较好。为保证精确预测航空发动机RUL，预测点以不低于70%的测试数据。

图17、图18分别显示了测试集100台航空发动机的RUL预测结果及其误差。绝对误差值范围为0.15～10.50，提出的多层LSTM模型在不同航空发动机RUL预测中效果良好，再一次验证了有效性、适用性与通用性。

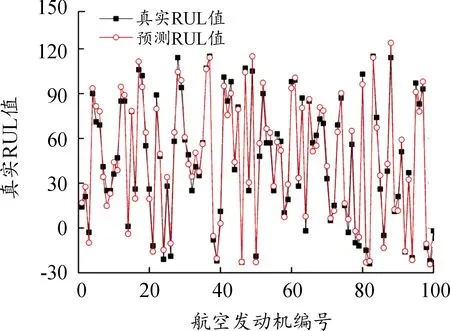
图17 100台航空发动机RUL预测结果曲线

图18 100台航空发动机RUL预测误差与绝对误差图

3.5 预测模型评估

预测模型评估作为模型适用性和可靠性的定量表征，为保证航空发动机安全运行与评估不确定性提供了支持，RUL预测模型需要更加全面分析与评估。一方面考虑到预测模型误差率增加的风险，另一方面客观存在潜在严重性故障发生的可能，航空发动机运行后期预测比早期预测的风险更大。因此，将设计的误差得分函数用于评估RUL预测，其不对称评分算法能够围绕真实RUL值，以评估超前与滞后预测。考虑到评估标准化并与其他模型对比分析，设置滞后预测参数为α1=10，超前预测参数α2=13。

利用误差得分函数，并结合多种评估指标，即MSE、FP、FN、MAPE、MAE、Std.Dev、MAD与MdAD以进行全面地模型评估，所得结果与其他预测模型的结果[15]如表4所示。

由表4可知，在航空发动机较长循环周期内，改进的多层LSTM模型预测性能优良。使用基于PCA的健康因子以RUL预测，通过使用不同的训练数据，网络训练能够按需完成，同时能够显着提高训练性能。针对航空发动机运行后期，误差得分函数对滞后预测的不对称高惩罚，而超前预测占最终误差得分的主导，有效地实现了评估超前与滞后预测。根据多种评估指标结果，本文所提出的智能预测模型是可靠的。