卫星时分多址信号高精度快速时频差联合估计方法

陈潇扬 邱乐德 李帅 李明 辛宁

(中国空间技术研究院通信与导航卫星总体部，北京 100094)

利用卫星测量未知电磁辐射源参数，以此确定未知辐射源的地理位置，是卫星电磁频谱感知领域的研究热点。目前，主要定位方法有测向定位、时差定位、多普勒频差定位，以及上述方法的组合定位等。时频差联合定位是利用多颗卫星，测量同一未知辐射源到达多颗卫星的到达时差和多普勒到达频差信息，以此确定辐射源的位置，具有精度高、所需设备少等优势。因此，对非合作信号的时频差参数估计，作为卫星频谱感知的基础，其估计性能决定了对目标辐射源的定位精度[1-2]。

国内外在时频差参数估计方面做了大量研究。传统互模糊函数算法通过搜索互模糊函数图峰值位置来实现参数估计[3]，该算法所需数据量大，计算复杂度高。基于该算法，许多时频差估计算法被提出。文献[4]中提出一种基于高阶统计量的时频差联合估计方法，利用高阶统计量减小相关噪声对参数估计的影响，该方法计算复杂度高。文献[5]中提出一种基于循环统计量的时频差估计方法，利用循环统计量来减小相关噪声的影响，该方法计算复杂度较高。文献[6]中提出一种基于长时间相干累积的时频差估计方法，采取滑动时延调整和相位补偿措施来实现长时间积分下的相干累积，可有效提高时频差参数估计精度，但该方法计算复杂度高。为降低计算复杂度，文献[7]中提出一种基于分维估计的时频差估计方法，将二维搜索问题转化为2个一维参数估计问题，但该方法在低信噪比下参数估计精度较差。上述现有方法不能有效兼顾计算复杂度和参数估计精度，因此无法有效应用于工程实践。此外，现有方法主要基于常规通信体制信号，对于特殊体制信号需要进行相应的优化设计。时分多址(TDMA)是无线通信中一种重要的信号复用方式，广泛应用于卫星移动通信系统，其主要特点是将整个信号划分为多个帧，每帧中包含多个时隙，不同用户信号占据不同时隙，以此增加传输效率。由于TDMA信号中同一用户信号时域的非连续特性，采用现有时频差估计方法对其进行时频差估计会出现以下问题：若仅利用单时隙信号进行时频差参数估计，由于积累时间短，参数估计精度较差；若积累较长的观测时间，多个用户信号在时频差参数估计时相互影响，使得参数估计精度及多个相关峰值的区分得不到保证。目前，针对TDMA信号的时频差参数估计研究较少，文献[8]中结合TDMA通信体制的特征，推导证明了多个时隙信号能量具有可累积性，提出一种基于解调分选的TDMA信号时频差参数联合估计方法。该方法首先对TDMA信号进行用户分选，对于分选后的单一用户信号使用传统互模糊函数算法估计时频差，但未给出未知协议条件下TDMA信号解调分选原理及具体处理流程，且计算量大，占用过多系统计算资源，不利于系统实时处理。

为解决上述问题，本文针对TDMA信号提出一种高精度快速时频差联合估计方法。所提方法在通信协议未知的条件下，通过TDMA信号检测、时隙分离、调制样式判别来分选不同用户对应的信号时隙，避免多个用户信号在时频差参数估计时相互影响；此外，通过时频差粗值估计、时频差精细值估计及二阶曲面拟合来降低计算复杂高，提高参数估计精度，从而实现TDMA信号高精度快速时频差估计。

1 TDMA信号高精度快速时频差联合估计方法

针对TDMA信号在时频差估计中存在多用户相互影响、估计精度差、计算复杂度高等问题，本文提出一种TDMA信号高精度快速时频差联合估计方法。首先，通过TDMA信号检测及解调分选获得主站不同用户对应的时隙信号；然后，利用分选后的主站各用户信号数据分别与辅站接收数据进行时频差粗值估计、精细值估计及二阶曲面拟合，从而快速获得TDMA信号各用户时频差参数的精确估计值。其具体过程如图1所示。

图1 方法过程

1.1 信号模型

对于2颗卫星所接收到的TDMA信号，假设其中共有P个用户时隙，由于卫星位置和运动状态的不同，辅站接收的某用户信号相对主站接收的该用户信号存在时延差和多普勒频差。主站接收的基带信号xm(t)和辅站接收的基带信号xa(t)可分别表示为

(1)

式中：t为时间；sp(t)为第p个用户信号，见式(2)；nm(t)和na(t)分别为主站和辅站所接收的噪声信号；τp为第p个用户信号到达主站和辅站的时差；fp为第p个用户信号到达主站和辅站的频差。

(2)

式中：Nf为主站数据中TDMA信号帧个数；Tr为帧长度；Tw为时隙长度；nf为帧号；κp(t)为第p个用户已调信号。

1.2 TDMA信号检测及解调分选

1.2.1 TDMA信号检测

通信信号由于编码、调制等过程，一般具有循环平稳特性，即在循环频率处具有非零值，而噪声为非平稳信号，其循环平稳特征理论上为零[9]。因此，可利用信号与噪声循环平稳特征的差异进行TDMA信号检测。对主站数据计算循环自相关函数，表达式为

(3)

式中：α为循环频率；τ为信号时延值。

对循环自相关函数进行傅里叶变换，得到循环谱密度函数Sα(f)，其表达式为

(4)

式中：f为频率。

判断循环谱密度函数图是否出现尖峰，若尖峰存在，可确定主站接收数据中存在TDMA信号。

1.2.2 TDMA信号时隙分离

TDMA信号以不同的时隙来区分不同用户，从而完成多址连接。本文采用基于小波阈值去噪和短时电平和的时隙分离方法实现TDMA信号不同时隙的准确分离[9]，实现过程如图2所示。

图2 TDMA信号时隙分离过程

对主站数据进行小波阈值去噪处理，以减小噪声对时隙分离的影响。首先，选择合适的小波基和分解层数[9]，对接收信号进行小波分解，得到对应的小波系数；然后，选择合适的阈值和阈值函数，对小波系数作阈值处理；最后，重构处理过的小波系数，得到去噪后的主站数据。

经去噪处理后，主站信噪比较高，信号幅度明显大于噪声幅度。因此，可通过表征信号瞬时时刻能量的短时电平和对主站接收的TDMA信号进行时隙分离，短时电平和定义为

(5)

式中：TL为时间窗长度；tq为第q个时间窗对应的时间序列。

计算各时间窗内短时电平和序列平均值σ，并以该均值作为阈值进行时隙初步分离，其表达式为

(6)

式中：σ=[c(t1)+…+c(tNc)]/Nc，Nc为电平和序列个数。

为避免时隙初步分离引入噪声时隙或将1个时隙截断，本文接着采用多参数优化措施对初步分离的时隙进行严格取舍。首先，利用最小时隙长度约束初步分离的时隙，避免小段时间内的强噪声对时隙分离的影响；然后，利用最小时隙间隔约束初步分离的时隙，避免将一个时隙截断，最终实现TDMA信号各时隙的精确分离。

1.2.3 TDMA信号调制识别及用户分选

由于不同用户信号的调制方式不同，需要对第1.2.2节分离的信号时隙进行调制样式判别。本文利用表征信号瞬时信息的特征参数设计多级分类器[10]，如图3所示，在每个节点上判断信号特征与相应门限值的大小，实现对各信号时隙的调制样式判别。

图3 信号调制识别过程

首先，计算待识别信号的零中心归一化瞬时幅度之谱密度最大值γmax，与门限t(γmax)进行比较，将待识别的信号分成(2ASK，4ASK，BPSK，QPSK)和(2FSK，4FSK)；对于判别类属于(2FSK，4FSK)的信号，计算待识别信号的零中心归一化非弱信号瞬时频率绝对值的标准偏差σaf，与门限t(σaf)比较，将其分成2FSK和4FSK；对于判别类属于(2ASK，4ASK，BPSK，QPSK)的信号，计算待识别信号的零中心非弱信号段瞬时相位非线性分量绝对值的标准偏差σap，与门限t(σap)比较，将其分成QPSK和(BPSK，2ASK，4ASK)；对于判别类属于(BPSK，2ASK，4ASK)的信号，计算待识别信号的零中心非弱信号段瞬时相位非线性分量的标准偏差σdp，与门限t(σdp)比较，将其分成BPSK和(2ASK，4ASK)；对于判别类属于(2ASK，4ASK)的信号，计算待识别信号的零中心归一化瞬时幅度绝对值的标准偏差σaa，与门限t(σaa)比较，将其分成2ASK和4ASK。下面为各判别参数的计算公式[11]。

γmax=max(|DFT(Acn(i))|2/N)

(7)

(8)

(9)

(10)

(11)

根据各时隙对应的调制样式，能够有效分选P个不同用户对应的信号时隙数据，为后续时频差估计奠定基础。

1.3 TDMA信号时频差估计

1.3.1 时频差粗值估计

对于分选得到的主站每个用户信号时隙，仅在该用户的通信时隙内保留信号与噪声，通信时隙外的数据进行置零处理，以减小时隙外噪声对时频差估计的影响[8]。本文基于聚焦傅里叶变换(ZFFT)思想[12]，利用处理后的主站第p个用户数据与辅站接收数据进行快速时频差粗值估计。对于主站和辅站接收数据，其离散互模糊函数可计算为

χ(Mp,Kp)=

(12)

式中：xm，p(n)为分选后的主站第p个用户数据；xa(n)为辅站接收数据；n为离散时间序列；Mp为离散时差序列，其取值范围代表时差搜索范围；Kp为离散频差序列，其取值范围代表频差搜索范围。通过搜索函数χ(Mp,Kp)的最大值可以获得时差和频差的测量值，若(Mp,max,Kp,max)为函数最大值对应坐标，则Mp,maxΔτ为第p个用户主站和辅站之间的时差测量值；Kp,maxΔf为第p个用户主站和辅站之间频差测量值；时差分辨率Δτ=Tsum/Ns；频差分辨率Δf=fs/Ns；Ns为总的信号点数；Tsum为所处理信号的持续时间；fs为采样频率。

由式(12)可知，互模糊函数可以看作混合积信号r(n,Mp)的Ns点离散傅里叶变换，得到其在[-fs/2,fs/2]的取值，该区间远大于实际频差参数的取值区间，从而造成计算资源浪费。

为减小计算量，本文利用ZFFT思想进行互模糊函数计算，首先对混合积信号r(n,Mp)进行低通滤波和降采样处理，使得信号频谱接近于频差取值区间，其表达式为

(13)

rM(m,Mp)=rN′(mD,Mp)=

(14)

式中：h(l)为滤波器系数；m为下采样后的离散时间序列；D为下采样倍数；下采样后的混合积信号长度M=Ns/D。

此时，互模糊函数可看作混合积信号rM(m,Mp)的M点离散傅里叶变换，其中M≪Ns。

对于任一时延序列值Mp，将处理后的混合积信号进行傅里叶变换，可得互模糊函数在时差MpΔτ处的切片。由于无法提前预知时频差参数取值范围，因此在时频差粗估计时，以步长Δτ进行搜索效率较低，因此可以选择在大时差搜索范围内以较大步长LcoarseΔτ来改变时延值，并对混合积信号进行傅里叶变换，其中，Lcoarse为所选择的步长倍数。如式(15)所示，可得到该搜索范围内的粗略互模糊函数图，经谱峰搜索后，能够获得时频差粗估计值。

χ(Mp,coares,Kp)=

(15)

此时，Mp,coares取值范围为[-Tcoarse′,Tcoarse′]，取值间隔为LcoarseΔτ，Tcoarse′为粗估计时差取值范围；Kp取值范围为[-fs/2D,fs/2D]，取值间隔为Δf。通过搜索函数最大值位置可以获得时差的粗估计值τp,coares与频差的粗估计值fp,coares。

1.3.2 时频差精细估计

以获得的时频差粗估计值为中心，进一步减小时差搜索范围，在该时差搜索范围内按照较小步长改变时延值，并对混合积信号进行傅里叶变换，如式(16)所示，可获得精细互模糊函数图，经谱峰搜索后，从而获得时频差精细估计值。

χ(Mp,fine,Kp)=

(16)

此时，Mp,fine取值范围为[(τp,coares-Tfine′),(τp,coares+Tfine′)]，取值间隔为Δτ，精细估计时差取值范围Tfine′≪Tcoarse′；Kp取值范围为[-fs/2D,fs/2D]，取值间隔为Δf。通过搜索函数最大值位置可以获得时差的精细估计值τp,fine与频差的精细估计值fp,fine。

1.3.3 二阶曲面拟合

由于信号间时频差是连续的，其可能并不恰好位于互模糊函数图划分的网格点上。为进一步获得真实的时频差参数，本文采用曲面拟合方法来提升参数估计精度[12]。假定互模糊函数图为二阶曲面，其拟合函数为

|A(τp,fp)|=c1τp2+c2τpfp+c3fp2+

c4τp+c5fp+c6

(17)

式中：c1,…,c6为拟合函数的系数。

在精细互模糊函数图谱峰位置A00(τp,fine,fp,fine)周围，选择其周边8个点A--,A0-,A+-,A+0,A-0,A-+,A0+,A++，将其代入拟合方程，可得

(18)

因为c6对于下文公式推导无影响，为行文简略，将其忽略。

将二阶曲面拟合函数分别对τp和fp求导，并分别求取极值点，可获得TDMA信号第p个目标用户的时差频差的最终估计结果τp′和fp′，其表达式为

(19)

综上所述，本文方法通过时频差粗值估计、精细估计及二阶曲面拟合，能够有效提升参数估计精度，降低计算复杂度，实现TDMA信号时频差参数高精度快速估计。分析总结所提方法及其他传统方法的时频差参数计算复杂度，如表1所示，表中Ns为上文中总的信号点数。

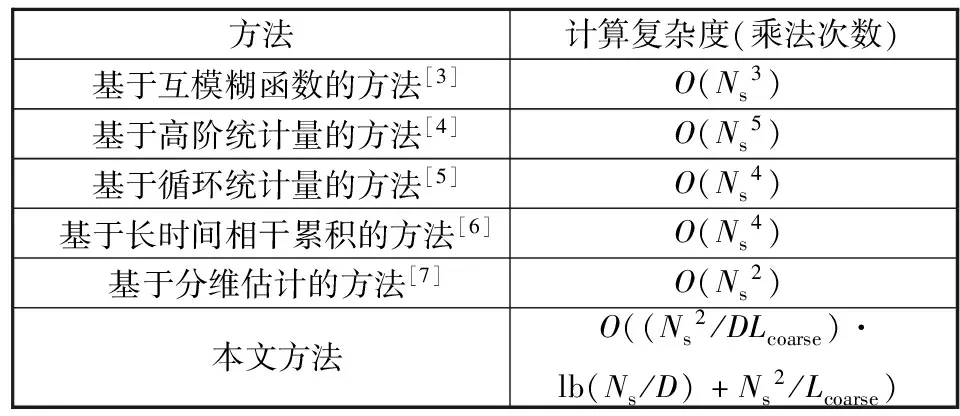
表1 不同时频差估计方法计算复杂度

2 仿真验证

2.1 TDMA信号检测

在卫星通信系统中，1个接收机的接收范围内经常出现用户稀少的情况，为不失一般性，假设TDMA信号每帧包含2个时隙，即代表2个用户，分别使用BPSK调制方式与QPSK调制方式，信号采样频率fs=10 kHz，信号频率fc=500 Hz。噪声为高斯加性白噪声，主卫星站接收的各用户信号信噪比均为20 dB，辅站接收的各用户信号信噪比均为0 dB。对主站接收的数据进行TDMA信号检测，循环谱密度函数图如图4所示。

观察图4(a)可知，当主站接收数据为纯噪声时，循环谱图无明显尖峰出现；由图4(b)可知，当主站接收数据中存在TDMA信号时，循环谱图在循环频率α=0，谱频率f=±500 Hz和α=±1000 Hz，f=0 Hz处出现明显尖峰，此时能够有效检测出TDMA信号。

图4 主站接收数据信号检测结果

2.2 TDMA信号时隙分离

经过TDMA信号检测后，对含有TDMA信号的主站数据进行时隙分离，仿真参数同第2.1节，其结果如图5所示。图5(a)为经过TDMA信号检测后获得的信号，由于信号能量大于噪声，可以较为明显地观察到信号波形，但是由于噪声的存在，不能准确地分离各个时隙；观察图5(b)可知，主站TDMA信号经小波阈值去噪处理后，噪声功率明显降低；对去噪后的数据利用短时电平和进行时隙初步分离，图5(c)为分离结果，大部分信号所在时隙可以较为清楚地划分，但是此时仍会出现噪声时隙被误认为信号时隙和同一信号时隙被截断等问题，即为图中虚框所示；经多参数优化后，如图5(d)所示，TDMA信号所有时隙能够得到准确分离。

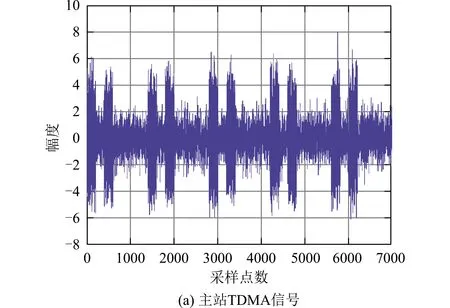
图5 TDMA信号时隙分离结果

2.3 TDMA信号时频差参数估计

对主站分离的各个时隙分别进行调制样式判别，并在此基础上，分选多个用户对应的信号时隙。下面分别采用传统互模糊函数方法和本文方法分别对TDMA信号进行时频差参数估计，其中，传统互模糊函数方法是直接利用主站、辅站接收数据进行参数估计；本文方法分别利用分选后不同用户对应的时隙数据与辅站接收数据进行时频差估计。

假设TDMA信号每帧包含2个用户，其中，第1个用户为BPSK调制，第2个用户为QPSK调制，信号采样频率fs=10 kHz，信号频率fc=500 Hz；用户1信号到达2颗卫星的时差、频差分别为τ1=100 μs，f1=10 Hz，用户2信号到达2颗卫星的时差、频差分别为τ2=1 ms，f2=100 Hz。噪声为高斯加性白噪声，主站接收的各用户信号信噪比均为20 dB，辅站接收的各用户信号信噪比均为0 dB。仿真结果如图6所示。

由图6(a)可知，利用传统互模糊函数方法可得到具有多个峰值的时频域二维相关图，此时无法有效辨别特定用户对应的峰值；由图6(b)和图6(c)可知，本文方法分别仅在用户1时频差参数值和用户2时频差参数值处形成尖峰，由图6(b)尖峰位置可得用户1的时差为τ1′=100 μs，频差为f1′=10 Hz，由图6(c)尖峰位置可得用户2的时差为τ2′=1 ms，频差为f2′=100 Hz，获得了2个用户准确的时频差参数。

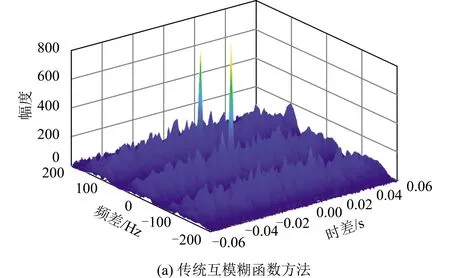
图6 2个用户条件下TDMA信号时频差参数估计仿真结果

假设TDMA信号每帧中包含4个用户，其中：第1个用户为BPSK调制，第2个用户为QPSK调制，第3个用户为2ASK调制，第4个用户为4ASK调制；信号采样频率fs=10 kHz，信号频率fc=500 Hz；用户1信号到达2颗卫星的时差、频差分别为τ1=100 μs，f1=10 Hz，用户2信号到达2颗卫星的时差、频差分别为τ2=1 ms，f2=20 Hz，用户3信号到达2颗卫星的时差、频差分别为τ3=500 μs，f3=-5 Hz，用户4信号到达2颗卫星的时差、频差分别为τ4=2 ms，f4=75 Hz。噪声为高斯加性白噪声，主站接收的各用户信号信噪比均为20 dB，辅站接收的各用户信号信噪比均为0 dB。仿真结果如图7所示。

观察图7(a)，传统互模糊函数方法所得时频域二维相关图，有一个较宽的主峰及许多高度较低的副峰。此时，由于各个用户时频差对应相关峰之间的间距较小，多用户之间互相影响，使得各个峰合成为了一个较大的主峰，无法有效测量各个用户的时频差参数。观察图7(b)～7(e)，利用本文方法形成的单一峰值，可以对不同用户进行分别观测，提高了准确性，由图7(b)尖峰位置可得用户1的时差为τ1′=100 μs，频差为f1′=10 Hz，由图7(c)尖峰位置可得用户2的时差为τ2′=1 ms，频差为f2′=20 Hz，由图7(d)尖峰位置可得用户3的时差为τ3′=500 μs，频差为f3′=-5 Hz，由图7(e)尖峰位置可得用户4的时差为τ4′=2 ms，频差为f4′=75 Hz，获得了4个用户准确的时频差参数，且计算复杂度低，实现了TDMA信号各用户时频差参数快速准确估计，可用于后续卫星频谱感知体系建设。

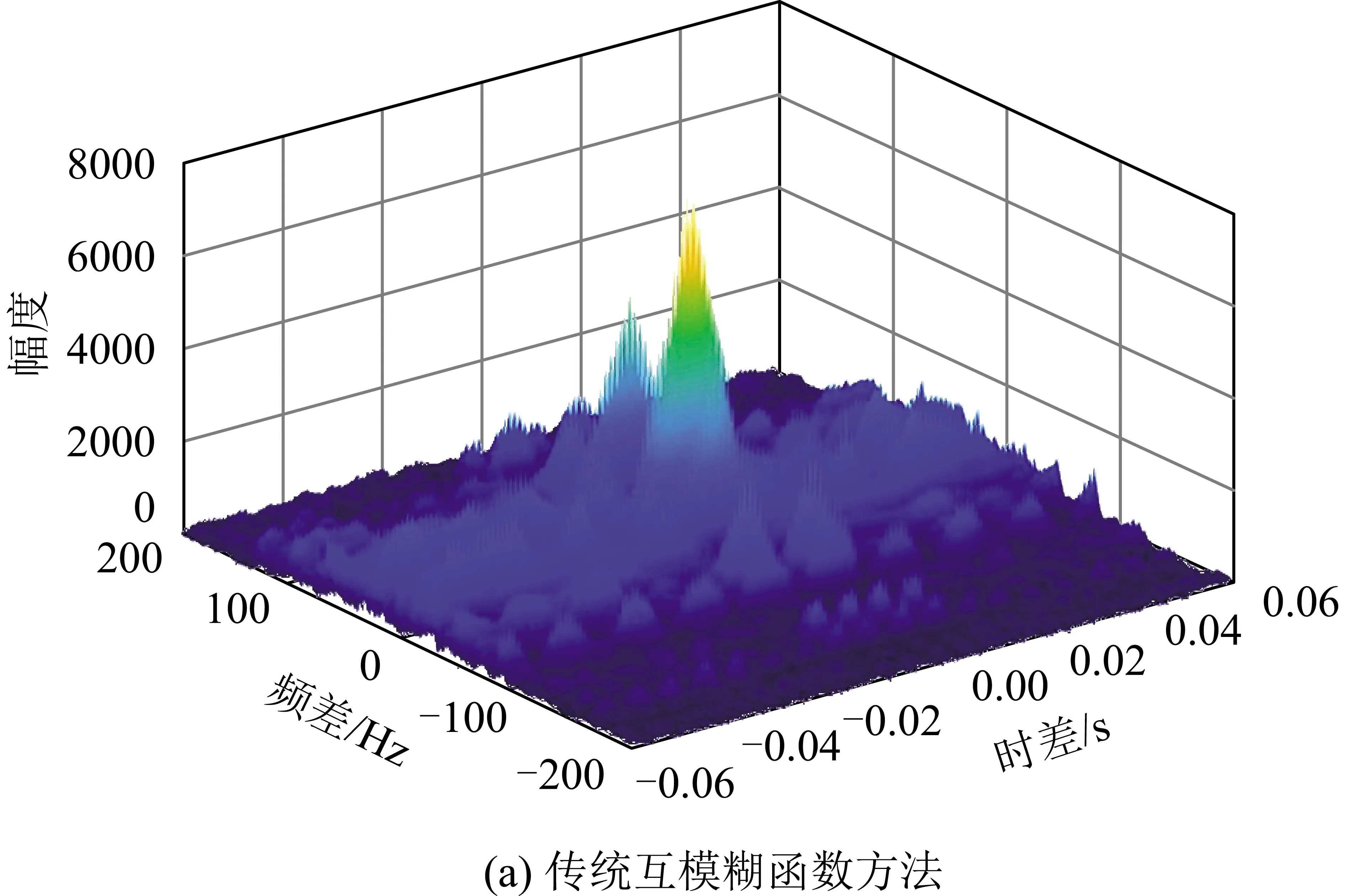
图7 4个用户条件下TDMA信号时频差参数估计仿真结果

3 结束语

本文针对卫星频谱感知领域中TDMA信号参数估计问题，提出了一种高精度快速时频差联合估计方法。该方法通过TDMA信号检测、时隙分离、调制样式判别分选主站接收数据中不同用户对应的信号时隙；基于主站分选后的各用户数据分别和辅站接收数据进行时频差参数估计，通过时频差粗值估计、时频差精细值估计及二阶曲面拟合提高参数估计精度，降低计算复杂度。计算机仿真结果表明：本文方法能够有效避免TDMA信号中各用户相互影响的问题，实现TDMA信号各用户时频差参数高精度快速获取，可为后续卫星频谱感知体系的建设提供理论支撑。