基于拓扑优化的航炮炮塔轻量化研究
2022-02-21申亚琳
刘 镔,李 勇,申亚琳
(西北机电工程研究所, 陕西 咸阳 712099)
1 引言
针对武装直升机近距离对地对空作战能力的需求,实现航炮武器的轻量化能有效提升武器系统与直升机适装性。航炮武器系统主要由自动炮,炮塔,供弹系统和随动系统等部分组成。其中,炮塔结构是承载自动炮和随动系统的重要支承构件,多为异型铸锻件。在射击时,航炮炮塔主要承受连续射击的冲击载荷,工作环境和受力情况较为复杂。实现航炮炮塔的减重不但可大幅减少整个系统的质量,也可使炮塔结构更为紧凑。
目前,针对结构的轻量化研究,一般采用拓扑优化的方法进行结构改进,从而为设计者在概念阶段提供基本的设计雏形。在火炮领域,钱林方等为解决冲击载荷下某自行榴弹炮炮塔的轻量化问题,利用基于遗传算法的拓扑优化方法对钢制焊接结构的炮塔体进行减重,实现了大口径火炮炮塔体的轻量化设计。齐可鑫等针对某导弹发射装置钢制导弹腿支架的轻量化问题,利用拓扑优化的方法对脚腿支架进行减重设计,确保其能承受发射冲击,并对其功能和安全性进行了验证。于存贵、薛松等对某多管火箭炮起落架和回转体进行拓扑优化设计以提高其战场快速机动性,其起落架为框架结构,承受连续冲击载荷。以上研究主要针对板材、框架的焊接结构部件而进行了拓扑优化,有效地减轻了部件的质量。而航炮炮塔为复杂异型铸锻件,对加工工艺性要求较高,射击工况多为承受连续冲击载荷,受力情况复杂。目前,关于航炮炮塔拓扑优化减重方面的研究较少。
针对航炮炮塔异型结构的轻量化问题,采用基于变密度的拓扑优化方法对炮塔结构进行优化,得到拓扑构型后,将减材形式定义为挖孔和减壁厚2种类型,并从中提取5个优化区域及其对应的范围值,使其分别对应均匀设计法中的设计因素和水平值,继而得到多种设计方案,针对每种方案进行静力学分析、模态分析和谐响应分析,获得结构应力、应变,模态频率,谐响应振幅和动刚度等变化规律并综合考量,从中优选出最佳方案,实现结构轻量化的设计。
2 炮塔体结构分析
航炮炮塔体是连接机体,支撑摇架,安装高低机和方向机的构件,其材料为205A高强铸造铝合金,结构如图1所示,规定射击方向为正方向,垂直于座圈向上为轴正方向,依据右手定则确定轴正方向。
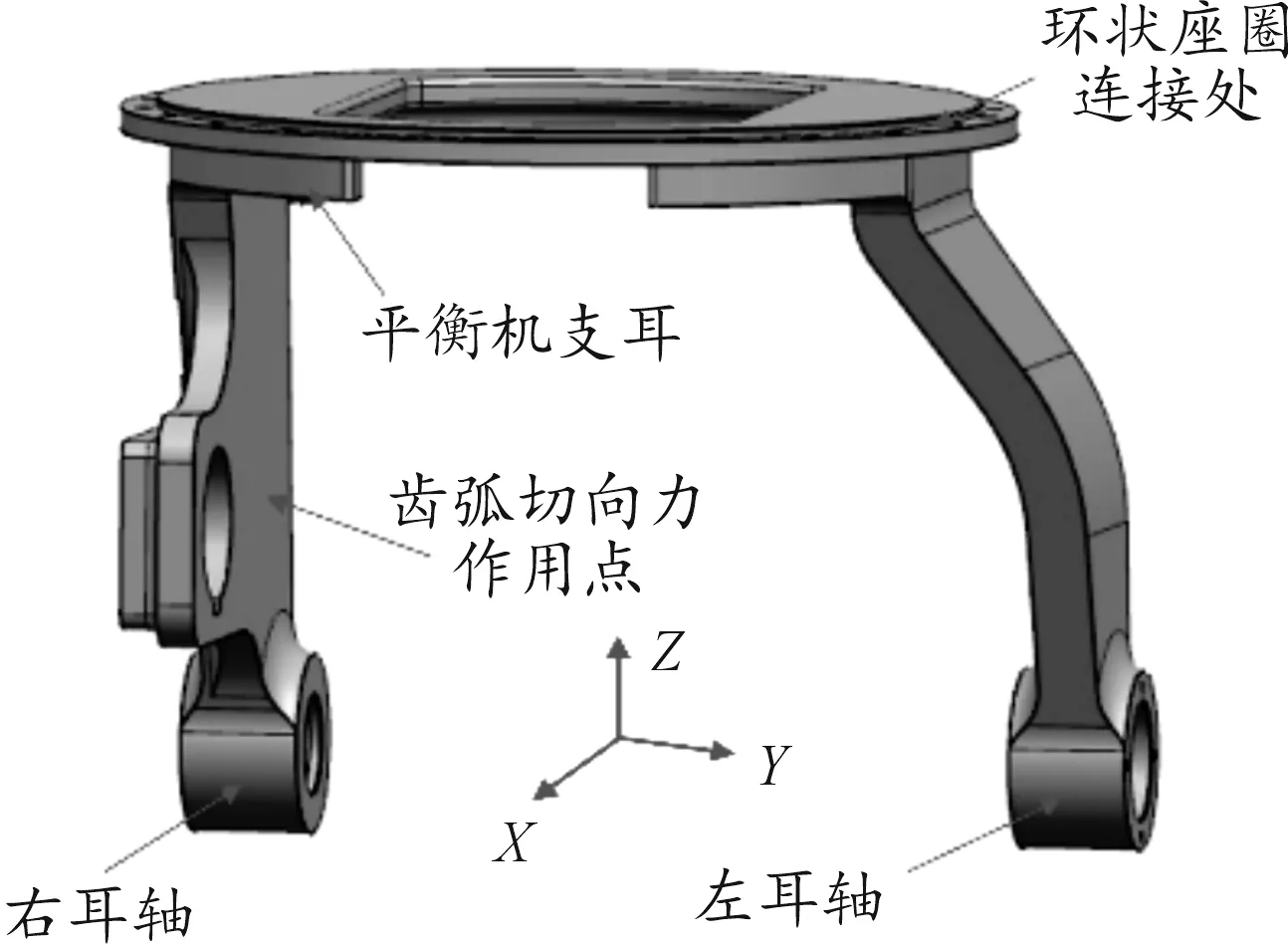
图1 原炮塔三维模型示意图
在射击过程中,膛底压力随射速和温度的升高,依据高射速高温条件下的内弹道曲线,炮塔的受力情况呈现出随时间变化的动态过程,炮塔各部位的受力也呈现出周期性。一般情况下,在0°射角时,最大炮膛合力时刻,受力情况最为极端,为保留一定的设计余量,后续的动静态分析中均选取最大膛压值作为初始输入条件。
弹丸发射后,膛底压力经自动炮传至摇架,由于质心偏离射击线,从而产生绕质心的偏心力矩,通过摇架耳轴和俯仰齿弧传到炮塔体,因此,经受力分析可知,炮塔体主要受到左右耳轴处由于炮膛合力偏心引起的支反力、、,俯仰齿弧产生的切向反力,平衡机产生的弹簧支撑力以及机体连接处的支撑反力、,其受力情况如图2所示。
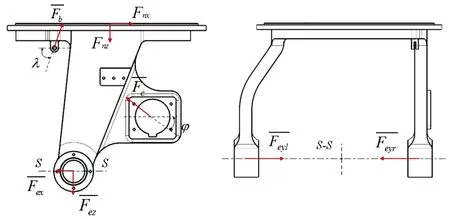
图2 炮塔受力分析示意图
其中,左右耳轴处支撑力和座圈顶部支撑力由摇架平衡方程及炮塔平衡方程计算得到,俯仰齿弧切向反力由电机扭矩确定,在0°射角时,电机输出扭矩为10 N·m,与射击线的夹角为81°,经3级传动传至齿弧;平衡机弹簧在0°射角时,预压缩量为164.6 mm,平衡机总刚度=7.77,与射击线的夹角为45°,则切向力和平衡机支撑力为:
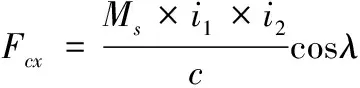
(1)
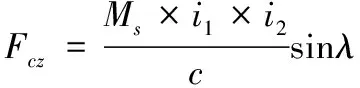
(2)
=cos
(3)
=sin
(4)
式中:=3045;=45分别为两级传动比;=200 mm为末级传动齿轮啮合点到中心线的距离。
经计算,各个部位的受力如表1所示。
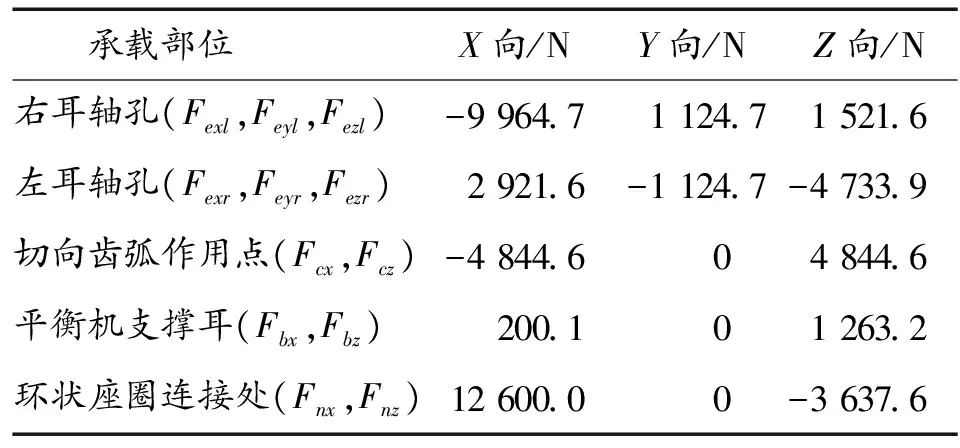
表1 炮塔各承载部位受力情况
3 炮塔体有限元建模及拓扑优化
3.1 基于变密度法的拓扑优化数学模型
变密度法的结构拓扑优化是一种基于有限单元集合的增删和保留的离散型结构拓扑优化问题,优化数学模型为:
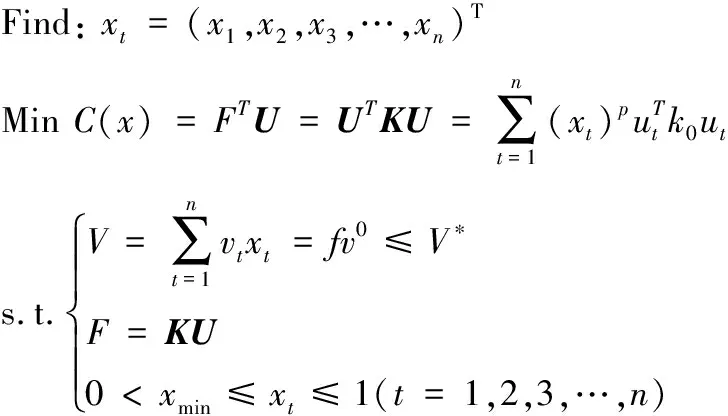
(5)
式中:为设计变量;为优化后结构体积上限;为总体刚度矩阵;为体积分数;为惩罚因子,炮塔所受外载荷集为{,,,,};结构位移向量为{,,,,}。
为得到设计变量对各参数的影响程度,求偏导进行灵敏度分析,具体可表示为:
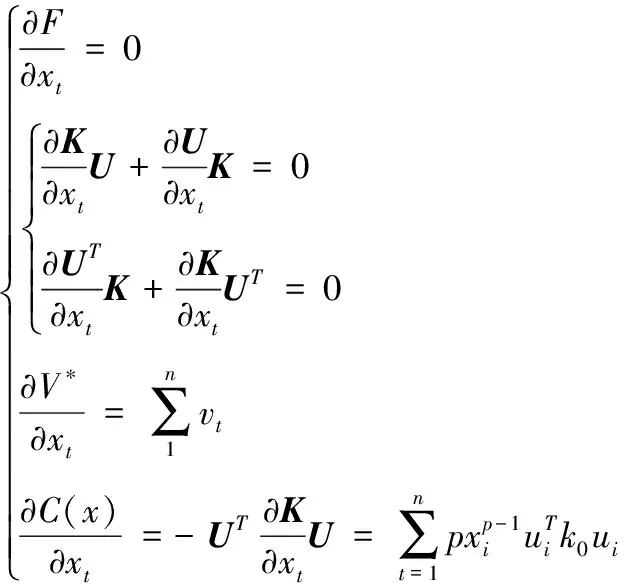
(6)
考虑以上所有因素,构造拉格朗日函数,推导其在结构应变能最小条件下的迭代关系,拉格朗日函数和启发式的变量更新可表示为:
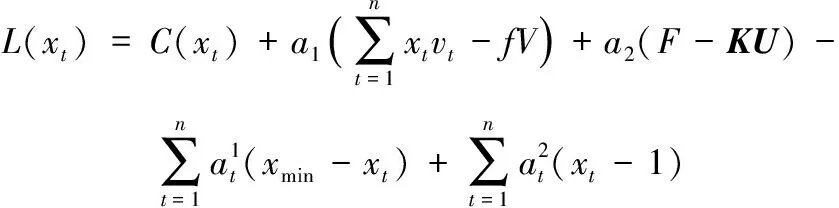
(7)

(8)
从上式中可得,结构的整体刚度与单元密度呈现正比关系。通过迭代改变各个单元的相对密度值,在约束条件下求取最小结构应变能,得到最优结构。
3.2 拓扑优化建模
依据现有的炮塔体结构,在Hpermesh软件中,对模型进行几何清理,选用四面体单元划分网格,网格大小为4.5 mm,总计生成4 834 568个单元,在各受力部位添加rbe2单元,保证主从节点自由度和刚性一致,并施加相应的作用力,在齿弧处施加固定约束,约束转自由度,在座圈顶部同样施加固定约束,约束除转的其他5个自由度,构建炮塔有限元模型。
原炮塔体的设计中,左右耳轴用于连接摇架,切向力作用点用于连接俯仰电机,与齿弧配合完成俯仰运动,平衡机弹簧用于补偿俯仰力矩,这些运动功能区域划分为为非设计区域,其他部分划分为为设计区域。在Optistruct软件中,建立基于SIMP插值的变密度法拓扑优化模型,模型单元密度为设计变量,体积最小化为设计目标,力约束和位移响应保证刚度条件。通过插值函数对中间密度单元进行惩罚,使优化后各单元的密度多集中于低密度0和高密度1。因此,取03密度阈值即可去除不必要的所有低密度单元,保留结构功能和刚强度需要的高密度单元,优化后的模型如图3所示。
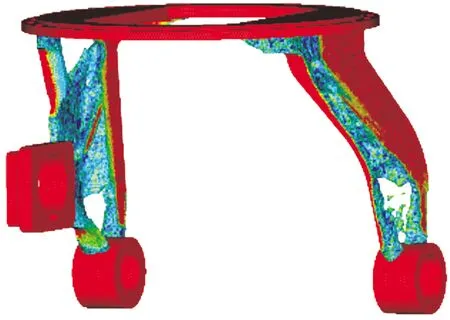
图3 优化后的炮塔拓扑构型示意图
图3中可以看出,炮塔拓扑构型的两支撑臂处存在较多减材区域,其中实心结构区域密度高,材料保留,空心结构区域密度低,材料去除。优化后的炮塔体结构的右臂存在两处孔洞,左臂存在一处孔洞,两臂均有不同程度的壁厚减薄。采用机加工的方式难以实现上述构型的制造,因此,需要考虑加工工艺性等因素,对炮塔拓扑构型进行再设计,以实现炮塔结构的工程化应用。
4 基于均匀设计法的方案改进
在概念设计阶段,拓扑结构优化分析结果可用于指导产品的形状设计,但应用于实际工程时,由于工艺和装配条件的限制,无法直接应用于工程实际。因此,获得航炮炮塔体拓扑优化密度分布云图后,按照高密度区保留,低密度区减薄的原则,同时考虑加工工艺性及与其他部件的装配关系,对炮塔体进行再设计。对于两支撑臂上的异型孔利用工艺性更好的圆孔代替,通过将三维拓扑构型转化为二维工程图,提取其内外接圆直径作为最小、最大直径,取整后以3 mm为间隔对直径范围进行划分,得到7组圆孔直径值。对于壁厚范围,最大壁厚即原始壁厚是通过强度计算所得,最小壁厚是通过量取优化后结构二维工程图中的最薄处尺寸所得,并以1 mm作为间隔对壁厚范围进行划分,得到7组壁厚值。具体改进如下:
1) 右臂上部异形孔提取其内接圆(=77.5 mm)和外接圆(=94.2 mm)并简化为圆孔A;
2) 右臂下部异形孔提取其内接圆(=67.7 mm)和外接圆(=86.4 mm)并简化为圆孔B;
3) 左臂下部异形孔提取其内接圆(=76.9 mm)和外接圆(=96.1 mm)并简化为圆孔C;
4) 右臂壁厚T1最大壁厚34 mm,最小壁厚28 mm;
5) 左臂壁厚T2最大壁厚36 mm,最小壁厚30 mm。
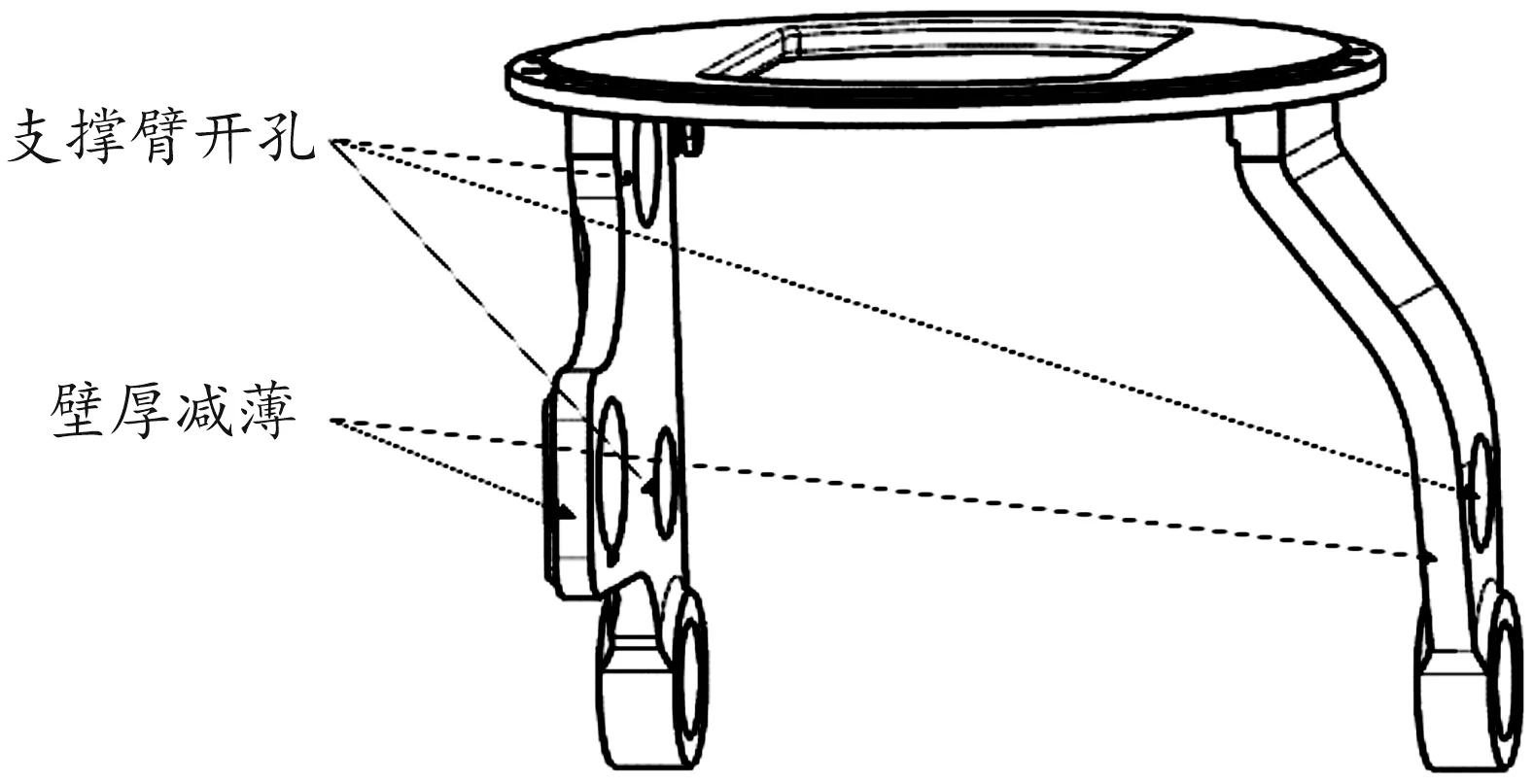
图4 优化后的方案5炮塔体结构示意图
均匀设计法能在提高效率的基础上反映整体的主要特征,并大大降低设计方案的数量。由此,利用均匀设计法进行改进方案设计,将圆孔A,B,C和壁厚T1、T2共5个变量作为设计因素,对应的直径和壁厚作为水平值。依设计因素和水平值构建(7)均匀设计表,其结果如表2所示,并依表对原模型进行改进,以方案5为例,改进后的模型如图4所示。
5 炮塔静力、模态与谐响应分析
对炮塔结构进行挖孔和壁厚减薄会造成一定程度的刚强度下降以及模态频率和动刚度的变化,因此,本文将从静、动态两个方面对改进后结构进行评价,在保证性能的基础上选取最佳方案。

表2 拓扑优化改进方案均匀设计表U7(75)
5.1 静力学分析
对改进前后的炮塔结构分别进行静力学分析,提取最大应力和应变值并测量质量如表3所示,其中S代表原始模型,P1代表方案1,以此类推。
结果表明,改进前后最大变形均出现在左耳轴连接处,最大应力出现在右臂与座圈的连接处。其中,改进后方案的应力、应变值存在不同程度的增大,这与结构壁厚减薄程度和开孔大小有关。在7组改进方案中,方案4和方案5的应力应变值与原始数据的差值不超过0.1 mm和6 MPa,与原有方案误差在10%以内,具有较好的刚强度,方案5应力、应变如图5所示。
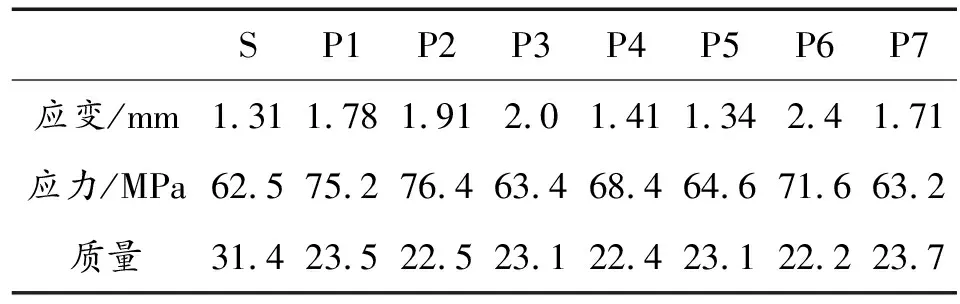
表3 改进后炮塔模型应力、应变、质量
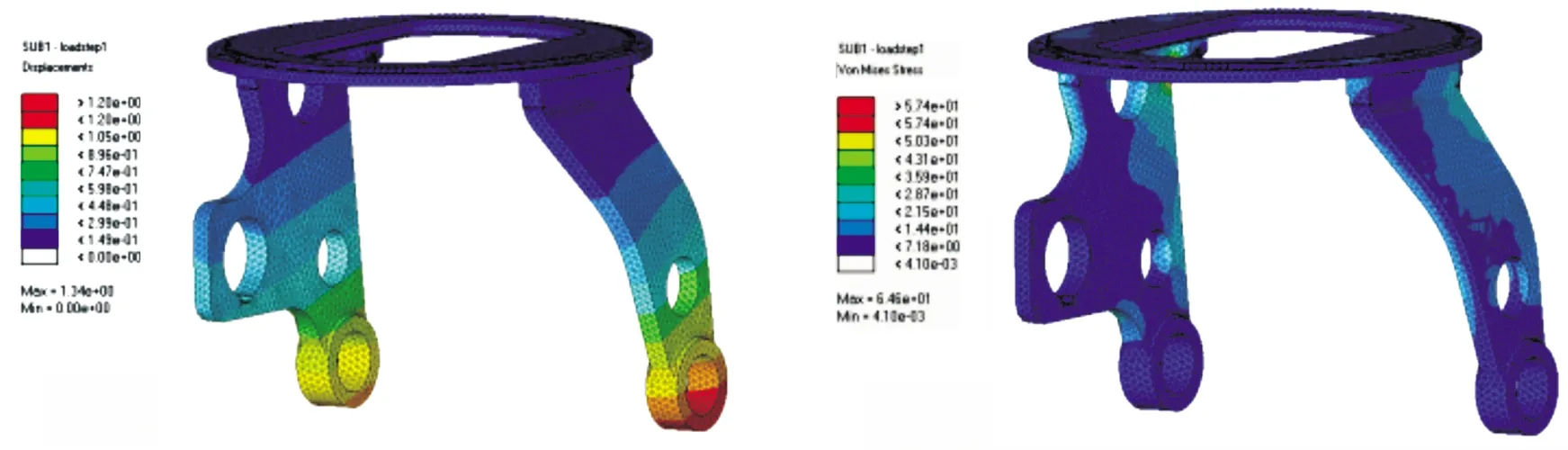
图5 方案5应力(左)、应变云图(右)
5.2 模态分析
对炮塔体进行全约束模态分析,得到结构的固有振动特性,包括各阶固有频率及对应的模态振型。由于炮塔为连续体结构,其低阶频率一般更能反映结构的振动特性,因此选取前12阶模态。在ANSYS Workbench软件中,结合炮塔实际安装情况,对炮塔顶部座圈处施加全约束,各方案结果如表4所示,表中列出了炮塔原始结构和优化后7种不同方案的前12阶模态固有频率,限于篇幅长度,仅列出方案5前4阶模态振型如图6所示。同时,从振型图中得到,不同方案相同频率对应的模态振型一致。
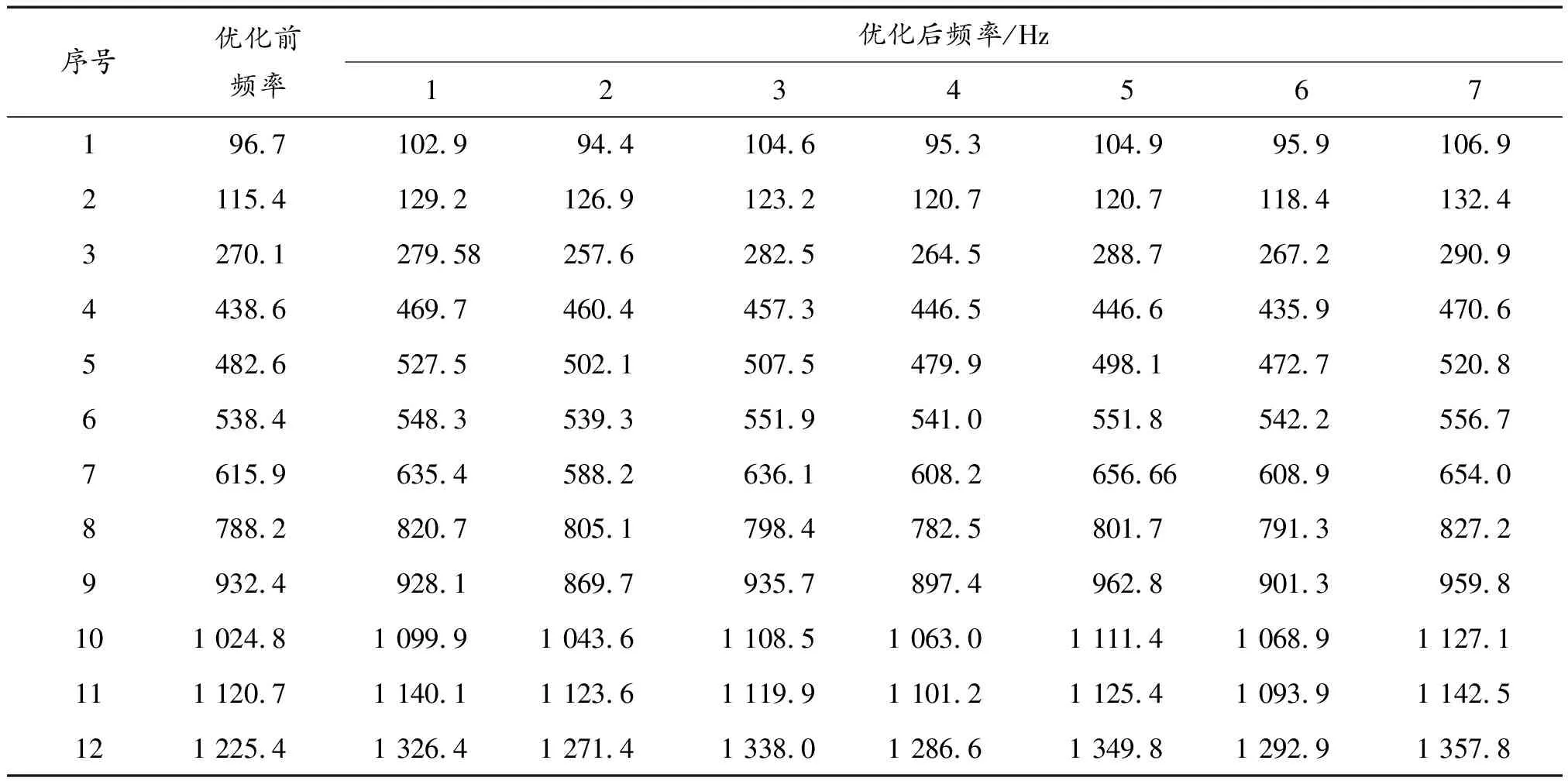
表4 炮塔结构采用各方案优化前后模态响应结果
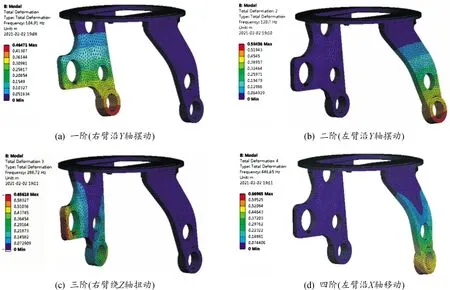
图6 方案5炮塔体前4阶振型云图
从模态固有频率值对比结果中可得,方案1、方案3、方案4、方案7在原方案的基础上,低阶模态频率与原方案相比均有所提升,前六阶模态频率平均提升高于10%;同时,在射击过程中,射频一般控制在3~10 Hz,低于炮塔模态最低频率,因此在射击过程中不会出现受迫振动产生的共振损伤。
5.3 谐响应分析
根据静力学分析和模态分析的结果可得,方案5与原方案的应力、应变差值最小,且低阶模态固有频率值增加显著,静、动态性能均有所提升。因此,为进一步保证航炮连发射击过程的安全性和可靠性,在方案5模态分析的基础上,进行谐响应分析,确定为炮塔结构变形影响最大的模态频率及其对应的结构变形形式。
谐响应分析中,依照实际的工况条件,在耳轴、平衡机支耳,齿弧切向力作用点等处的、、方向分别施加与静力学分析幅值等同且同相位的正弦激励,在座圈处约束全自由度,并参照模态分析结果设置频率空间的上下限,以整个炮塔结构为研究对象进行求解,获得其在不同频率正弦激励下的变形情况,继而分析改进前后炮塔在稳态受迫振动下结构的性能表现。选取、、方向对应谐位移的幅频特性进行分析,结果如图7所示。
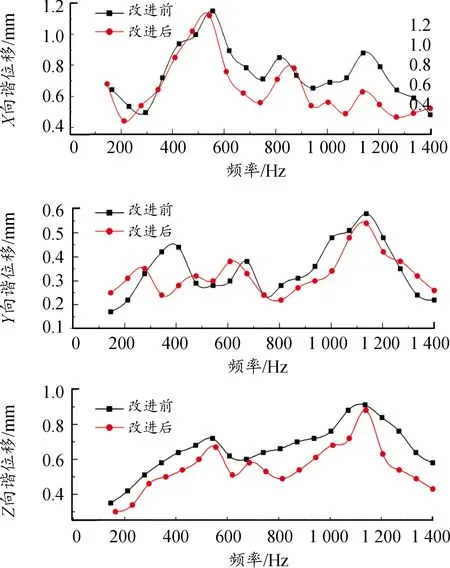
图7 原始炮塔体X(上)、Y(中)、Z(下)方向谐位移曲线
图7中可得,对改进前结构,方向最大振幅为1.15 mm,出现在555 Hz;方向最大振幅为0.58 mm,出现在1 136 Hz;方向的最大振幅为0.91mm,出现在1 136 Hz。与炮塔模态分析结果对比可得,542 Hz和1 136 Hz分别近似出现在第六阶和第十一阶模态,其对应的振动情况分为右臂的前后振动和左臂的扭转振动。
对方案5改进结构,炮塔体方向最大振幅为1.12 mm,频率为542 Hz;方向最大振幅为0.54 mm,频率为1 140 Hz;方向最大振幅为0.88 mm,频率为1 140 Hz,其同样对应第6阶和第11阶模态振型。、方向最大振幅较改进前下降0.03 mm,向振幅下降0.04 mm,且因结构的改变导致最大振幅与原方案对应的频率不重合。由于原方案遵循保守设计原则,采用大安全系数,因此只需保证改进方案与原方案静动态特性相当,即可满足性能要求。
为量化变形情况,引入动刚度表征各方向最大谐位移及其对应的振动形式的变形程度。以,表征动刚度及其变化系数,计算改进前后炮塔在、、方向的动刚度和变化系数如式(9)、式(10)所示,计算结果如表5所示。
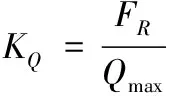
(9)
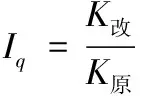
(10)
式中:代表、、三方向的最大位移。
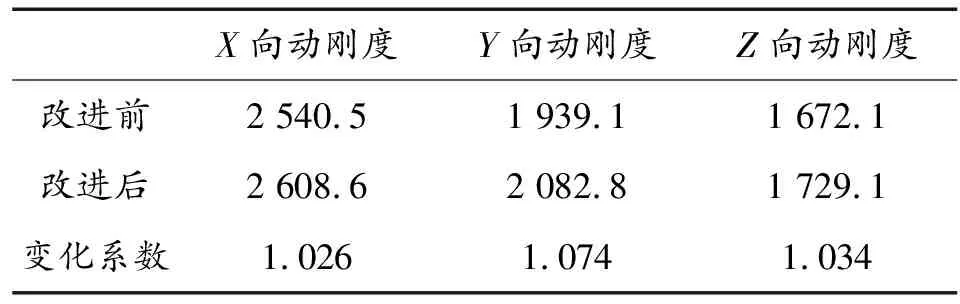
表5 改进前后各向动刚度
动刚度计算结果可得,方向的动刚度增长27,方向的动刚度增长74,方向的动刚度增长34,变化系数均大于1,结构刚度性能与改进前有所提升。
同时,从图7中也可得到,各方向的谐响应曲线变化趋势具有一致性,、方向最大振幅均出现在较高频段,向出现在较低频段,因此结构对、方向的低频载荷变化更为灵敏。次最大振幅及其他频率点对应的谐位移与原方案相比也存在不同程度减小,使得整个刚度得到提升。确保炮塔结构在不同频率范围内运行更加可靠。
6 结论
1) 采用拓扑优化、均匀设计、静动态分析等相结合的方法对航炮炮塔进行优化改进,在同时保证加工工艺性和静动态性能的前提下,实现了航炮炮塔结构减重8.3 kg,占原有质量的26.4%,达到了航炮炮塔轻量化的目标,验证了方法的有效性。
2) 改进后炮塔结构的动态性能得到全面提高,前6阶模态频率平均提高11.5 Hz。、、方向谐响应最大位移值与原始方案相比均有下降,动刚度分别增长2.7%,7.4%和3.4%。同时,在其他外界激励频率下,相同频率振动幅值减小,使得航炮炮塔动态性能更优。
