证券投资组合的实证研究

摘要：本文基于均值-方差投资组合模型，找到满足不同期望收益的条件下，风险最小的投资组合，来达到最优资产配置的目的。通过选取来自各行业的十支沪深股市A股股票及相关数据，对该理论模型进行实证检验，验证其科学性与实用性。最终得到在不允许卖空的条件下，满足预期投资收益的最优投资组合。

关键词：均值-方差投资组合模型;投资组合;实证检验

一、引言

想要在证券市场获取得稳定的收益并非易事，来自全球的投资者都为此目标不断努力，因而对股票投资组合的深入研究，不仅起着提高投资者平均素质的影响作用，更体现了规避市场参与者盲目投资、完善金融市场的研究价值。1952年，Markowitz提出了金融学的基础理论——投资组合理论，均值-方差投资组合模型便是其中重要的组成部分，该理论用均值表示收益、方差衡量风险作为建模的基础，其核心思路是在限定风险相同的条件下，投资者获得最大收益，或是在限定收益相同的條件下，投资者受到的风险最小[1]。本文将在均值-方差投资组合模型的基础上构建相关股票投资组合模型，并进行实证分析来验证其合理性。

二、理论基础与相关文献综述

投资组合理论是将不同资产进行相关配置的行为理论。Markowitz用均值表示收益、方差衡量风险作为建模的基础，以投资组合理论开创投资学先河，随后国内外学者对投资组合理论进行了更进阶的研究。主要模型有：单因素模型、资本资产定价模型（CAPM）、套利定价模型（APT模型）、自回归条件异方差模型（ARCH）以及对多阶段情形等，这使得现代证券投资组合理论更加完善[2]。

均值-方差投资组合理论的背景是：在某一时间段内，投资者用有限的资金进行投资。在期初，投资者将资金在各类证券上进行分配、购买，在限定时间结束后卖出，这也意味着投资者需要从所有可能的投资组合中选取一个最优的组合来进行投资[3]。投资者将会面对两个选择：一、在一定风险下，要求最高收益率;二、在一定的收益率下，要求最低风险。当然，最好的情况是能在风险与收益率两者之间获取最佳平衡点。基于以上解释的投资组合理论即为均值-方差投资组合理论。

均值-方差理论的成立需基于如下的几个假设条件[4]：

①证券市场是有效的;

②投资者是理性的，对风险是厌恶的;

③投资者要求较高的期望收益率以及较低的风险;

④针对证券的收益率，存在相关性

三、研究方法设计

本文研究方法以均值-方差投资组合理论为基础，通过建模对股票的投资组合进行实证。通过限定股票投资组合中的预期收益、兼顾风险偏好，结合有效前沿等理论，得到了有最优解的投资组合均值-方差模型：

目标函数：

min σ2p =W’ΩW

RP=Σωiri

假设条件：

Σωi =1，ωi>0 （不允许卖空）

其中，σ2p为投资组合的方差，W=（ω1，ω2， ...ωN）为各支股票所占权重构成的矩阵，RP为投资组合收益，ri为第i支股票的收益率，ωi为股票i在投资组合中的权重，Ω为各支股票的协方差矩阵。

通过上式可得，在给定预期收益率的限制条件下，求出各支股票在投资组合中所占权重ωi的最优解，使投资组合的风险σ2p最小。其现实意义是，投资者在其期望的收益率下，通过上述方程，计算得出每支股票所占的投资比例，来使总体投资组合的风险最小化。

四、数据与实证结果

本文选取了来自各行业的十支沪深股市A股股票所选股票为：上海机场（600009）、上海电力（600021）、贵州茅台（600519）、中国联通（600050）、中青旅（600138）、圆通速递（600233）、海澜之家、（600398）、光明乳业（600597）、中国银行（601988） 、强生控股（600662）。并运用下述公式计算日收益率：

Rt=（Pt- Pt-1）/ Pt-1

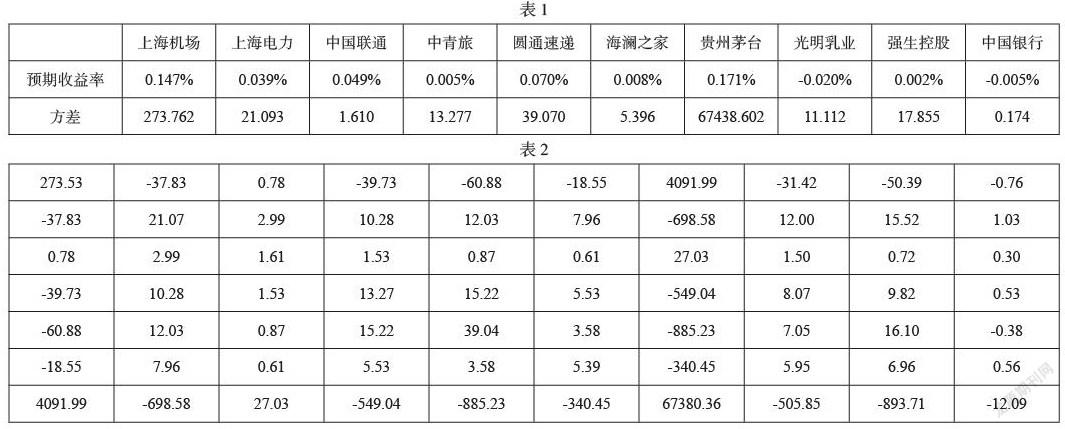
结合均值-方差模型，对各投资组合的收益率与风险水平进行比较，求得各权重配置最优解，达到资产的最优配置。各类资产的预期收益率和方差以及各类资产的协方差见表1和表2：

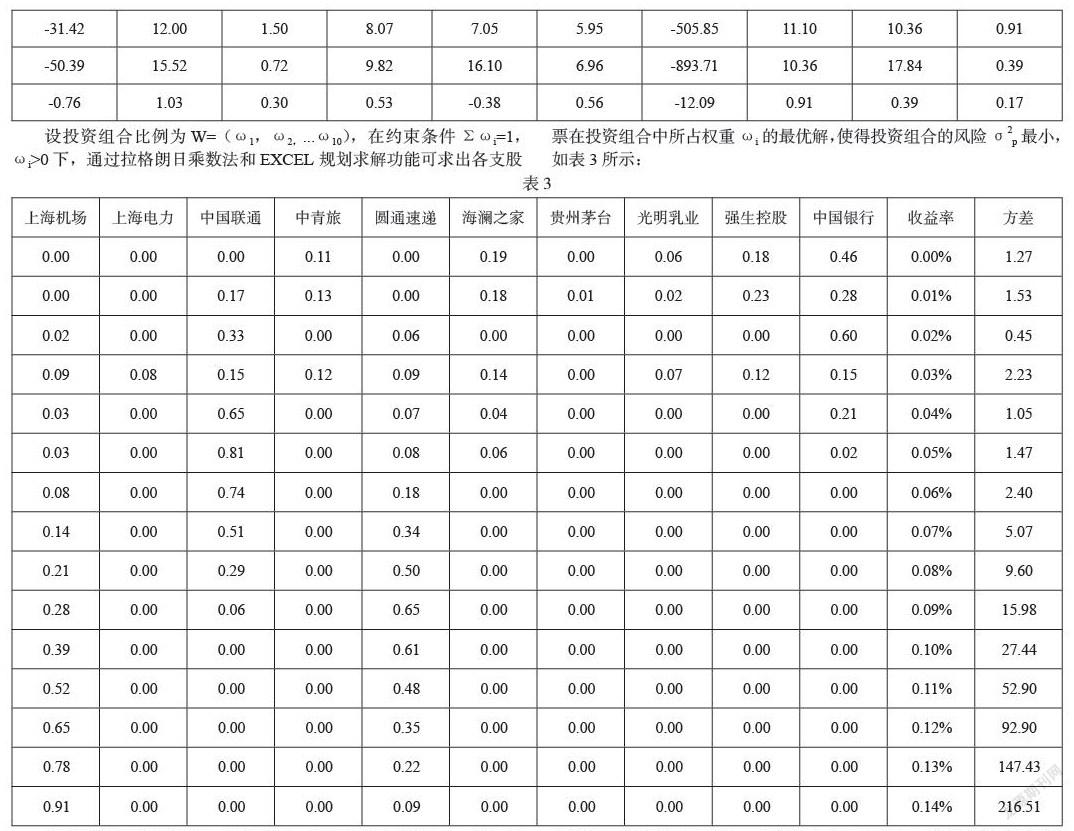
设投资组合比例为W=（ω1，ω2， ...ω10），在约束条件Σωi=1，ωi>0下，通过拉格朗日乘数法和EXCEL 规划求解功能可求出各支股票在投资组合中所占权重ωi的最优解，使得投资组合的风险σ2p最小，如表3所示：

在不同的期望收益率RP的条件下，利用所求出的权重ωi的最优解及各支股票的收益率、方差，以模型标准差为横轴的衡量单位、收益为纵轴的衡量单位，作出均值-方差投资组合的有效前沿，见图1：

上述结果表明，在由10支股票组成的投资组合中，该投资组合要达到在投资风险最小的条件下使得收益最大化（本文取日收益率为0.08%），应把21.2%的资金用于投资上海机场，29%的资金用于投资中国联通，49.8%的资金用于投资圆通速递。综上所述相关收益率统计量可得，中国银行有着较低得平均收益率，但其方差代表的风险也最小，因而可选取中国银行来确保低风险收益;贵州茅台有着最高的平均收益率，表示有着高收益的同时也存在着较高的风险。

五、结论

从均值-方差投资组合理论的有效前沿线上，我们很容易得出结论：投资者的预期收益率越大，投资组合方差也越大，这意味着越高的期望收益，投资将面临更高的风险。

计算结果具有一定的规律性：当期望收益率逐渐升高时，收益率、方差较小的股票（中国银行）权重逐渐下降，收益率、方差较大的股票（上海机场）权重逐渐增大。值得注意的是，随着期望收益率逐渐升高，收益率、方差最大的股票（贵州茅台）的比重却趋向于零。原因在于其惊人收益率与方差，在相同收益率、风险尽可能小的约束下，所求得的最优解排除了这支股票。

在本文中，我们得到了在不同预期收益率下最优的资产组合，并确定了这10只股票所对应的权重，投资组合的期望收益率和风险之间存在着动态的平衡，通过均值-方差模型在设定风险最小的情况下，往往投资组合的收益率并不能满足人们的期望，在实际生活中的运用具有局限性。此外，均值-方差模型对于大量股票的投资组合计算较复杂，实用性受到了一定的限制。

参考文献：

[1] 李勍. Markowitz的均值-方差模型在我国证券市场的实证研究[J]. 金融经济，2012，（24）：82-83

[2] 李方圆. 基于Markowitz理论的股票组合投资模型[J]. 现代商业，2019，（26）：137-138

[3] 黄璐. 基于均值-方差模型的股票投资组合构造分析[J]. 商业经济，2016，（8）：148-149

[4] 孙曼曼. 均值-方差模型在股市最优投资组合选择中的实证研究 [J]. 科技视界，2013，（12）：74

作者简介：金慧熠（1996- ），男，上海人，硕士研究生，研究方向：金融学。