混合种群算法HSO在求解RAP问题中的应用研究

李学宝，李东魁

（包头师范学院信息科学与技术学院，内蒙古包头，014030）

1 绪论

可靠性冗余分配问题（RAP）是可靠性研究领域的重要课题，在最近的半个世纪，RAP问题的研究取得了丰硕的成果[1]。一般的可靠性冗余分配问题（RAP）是NP-hard的，研究可靠性冗余分配问题的智能算法，具有重要的现实意义。

Yeh Wei-Chang[2]研究GRAP问题，即允许子系统有不同类型的元件可以选择的RAP问题时，给出了一个混合群体算法HSO，并讨论了基本原理、算法的有效性和正确性。为检验HSO算法在解决RAP问题中的有效性，本文对两个基本的RAP问题的模型[3-4]，设计HSO算法，进行模拟仿真，为进一步研究HSO算法在RAP问题中的应用打下基础。

1.1 假设

（1）网络和构成网络的元件有且只有两种状态，即正常工作状态和失效状态。（2）网络用一个无向图G =（V，E）表示，其中V表示网络结点（元件的连接）集合，E代表边（元件）的集合。s是源结点，t是汇结点。（3）结点是完全可靠的，永不失效。（4）网络是耦合的（Coherent）。（5）边的失效是统计独立的。某一边处于某种状态的概率是已知的。（6）每个元件（边）的可靠度和（或）价格和重量已知；（3）系统中各元件的失效是统计独立的；（7）失效的元件不可修复。

1.2 解的编码

可靠性冗余分配问题（RAP），在元件的可靠度已知的前提下，未知量是元件的冗余度。在SHO算法中，粒子（解）X的编码，代表的就是系统中各个元件的冗余度，因此，解X的编码方法为：由代表网络中各个元件的冗余度（整型）顺序组成行向量。

2 HSO算法求解单目标（费用最小）-单约束（可靠度 >=R0）模型

2.1 模型一

假设系统G=(V，E)由n个独立子系统组成，如图1所示，在每个子系统中使用相同的2-状态元件，Cn表示系统的总价格（这里仅仅考虑元件费用），R表示系统可靠性，ci表示第i种元件的单价，xi是第i个子系统第i种部件的个数，xi＞=1，R0是系统要达到预定的可靠度。pi是元件i的可靠度。

图1 串联-并联网络表示的RAP问题G=(V，E)

则单目标（费用最小）-单约束（可靠度>=R0）优化模型为：

2.2 算法

2.2.1 新解生成算法

初始解为X0，由X0出发生成一个新解的算法如下：

算法1

对X0的每个分量，如果随机数rand>=0.5，则新解的分量为X0的对应分量加上1，否则，为X0的对应分量减去1。

2.2.2 适应值函数

为修改基本HSO算法适应公式（1）-（2）表示的费用最小化单约束模型，定义新的适应值函数如下：

2.2.3 修改的HSO算法

将Yeh Wei-Chang[2]给出的HSO算法修改如下，有关算法机理、算法正确性等请参阅文献[2]。

算法2（伪Matlab代码）

Step0（初始化）以行向量的形式存储系统元件可靠度、价格等参数；设定压缩常数c1=c2=0.5，惯性权重w=0.9。

确定元件冗余度的上下界：varmax与varmin; 确定元件冗余度（变量）收敛速度的上下界velmax与velmin;n是元件个数，nc是粒子个数,令V=zeros(n,nc);A=zeros(n,nc);B=zeros(n,nc);CA=zeros(1,nc);Z=zeros(1,nt);这里 nt是总迭代次数。

Step1随机产生满足系统约束条件的nc个粒子存于矩阵A中；并将对应的适应值存于CA中；再将矩阵A存于矩阵B中（每个粒子的当前最优初始值）。

step3.2 对A中的每个当前解X，其对应的修订解Y，如果Y的适应值小于X的适应值，则将X替换为Y;否则，如果rand(1)>k(t)，（delt=X的适应值-Y的适应值;k(t)=cos(3.1416*delt^0.25*t^2/(1*10^6));）则将X替换为Y。

step3.3 如果A中每个当前粒子的适应值小于这个粒子的当前最优值的适应值，则将这个粒子的当前位置最优值进行更新；如果这个粒子的当前最优值的适应值小于全局最优解的适应值，则将全局最优解进行更新。

Step3.4 记录最优解对应的可靠度。

Step4输出最优解及对应的费用、重量约束、最优解可靠度；画出收敛曲线。

Step5算法终止。

2.3 模拟仿真

设图1模型中，由5个子系统组成，每个子系统中元件的正常工作概率和元件价格如下：p1=0.96，p2=0.93，p3=0.85，p4=0.80，p5=0.75；c1=3元，c2=12元，c3=8元，c4=5元，c5=10元，系统要求R0=0.9。

测试都是在微型计算机上进行的；计算机配置为：CPUIntel(R)Core(TM)i5-6500@3.20Ghz 3.20Ghz,内存 8GB,硬盘600Gb；操作系统为Windows10专业版；编程软件为MatlabR2015b。

算法参数的设置为：n=5,c1=c2=0.5;w=0.9,nc=100,nt=200,α=3。velmin=-0.5;velmax=0.5;varmin=1; varmax=4。初始解X0=[4,4,4,4,4]。

随机运行算法50次，算法都收敛到最优解Xgbet=[2,2,2,3,2];最小费用=最大费用=平均费用=81元；总的用时为32.67秒；算法一次运行的收敛曲线，见图2。

图2 算法2的一次运行给出的收敛曲线

2.4 算法比较

将文献中各种智能算法求解1.3算例的结果汇总如下表1。

表1 算法的比较结果汇总

由表1可知，HSO在求解1.3中问题时，考虑到目前微型计算机的运行速度都很快，运行算法所用时间不再是主要问题的前提下，HSO算法具有和PSO[5,15]算法、ACA[15]算法同样好的效果。另外，HSO算法的收敛情况和种群中的粒子数及迭代次数密切相关，当保持运行次数是200，但粒子数改为50个粒子，或保持粒子数为100个，但运行次数改为100的时候，随机运行算法50次，就会出现不可行解的情况。HSO算法出现这种情况的原因，从机理上看，可能是受到SA算法特征的影响。从上述实例的测试情况看，求解简单的单目标-单约束可靠性优化模型的时候，HSO算法并没有表现出它与PSO[5,15]算法的优势来。

3 HSO算法求解单目标（可靠度最大）-多约束（费用和重量）模型

3.1 模型二

系统由n个子系统串联组成，每个子系统又是由相同类型的元件并联构成，在有费用和重量约束条件下，选择合适的元件数目使得整个系统的可靠度最大[4]。

模型的数学表达式为：

为将公式（4）表示的模型转化为没有约束的优化问题，引入适应值函数如下：

其中α，β，γ是正整数。

3.2 算法

为讨论问题方便，将Yeh Wei-Chang[2]给出的算法，用伪Mablab语言描述如下：

算法3（伪Matlab代码）

Step0（初始化）以行向量的形式存储系统元件可靠度、价格等参数；设定压缩常数c1=c2=0.5，惯性权重w=0.9。

确定元件冗余度的上下界：varmax与varmin; 确定元件冗余度（变量）收敛速度的上下界velmax与velmin;n是元件个数，nc是粒子个数,令 V=zeros(n,nc);A=zeros(n,nc);B=z eros(n,nc); CA=zeros(1,nc); Z=zeros(1,nt);这里 nt是总迭代次数。

Step1随机产生满足系统约束条件的nc个粒子存于矩阵A中；并将对应的适应值存于CA中；再将矩阵A存于矩阵B中（每个粒子的当前最优初始值）。

Step2利用矩阵A，求出当前系统全局最优值Xgbest,即Xgbest是元件全局最优冗余度向量。

Step3 for t=1:nt

Step3.1

% 对种群A中的每个粒子(解)，按照PSO算法迭代公式修订后的新值存于矩阵Y中，然后按照阶跃函数[2]修订每个解。

step3.2 对A中的每个当前解X，其对应的修订解Y，如果Y的适应值大于X的适应值，则将X替换为Y;否则，如果rand(1)>k(t)，（delt=X的适应值-Y的适应值;k(t)=cos(3.1416*delt^0.25*t^2/(1*10^6));）则将X替换为Y。

step3.3 如果A中每个当前粒子的适应值大于这个粒子的当前最优值的适应值，则将这个粒子的当前位置最优值进行更新；如果这个粒子的当前最优值的适应值大于全局最优解的适应值，则将全局最优解进行更新。

Step3.4 记录最优解对应的可靠度。

Step4输出最优解及对应的费用、重量约束、最优解可靠度；画出收敛曲线。

Step5算法终止。

3.3 模拟仿真

系统由15个子系统组成，每个子系统都由相同元件组成，每个子系统元件的可靠性、费用与重量见表2[4]。

表2 系统元件参数

如果要求系统总费用C<=400元=C0，总重量W<=414kg=W0，nmax<=6。算法参数设置为：算法参数的设置为：n=15,c1=c2=0.5;w=0.9,nc=200,nt=1000,α=1，β=3，γ=1。velmin=-0.5; velmax = 0.5; varmin=1; varmax=6。选择初始解为X0=[3,3,3,3,3,3,3,3,3,3,3,3,3,3,3]。

算法求得的最优解为：X=[3,4,6,4,3,2,4,5,4,2,3,4,5,4,5]，此时系统最大可靠度为0.945613，系统费用392元，系统重量为414kg，本文最优解与文献[4]相同。随机运行50次算法，结果为：可靠性最大为0.945613，最小为0.944749，平均为0.944973，总时间为17.464秒。算法的收敛曲线见图3。

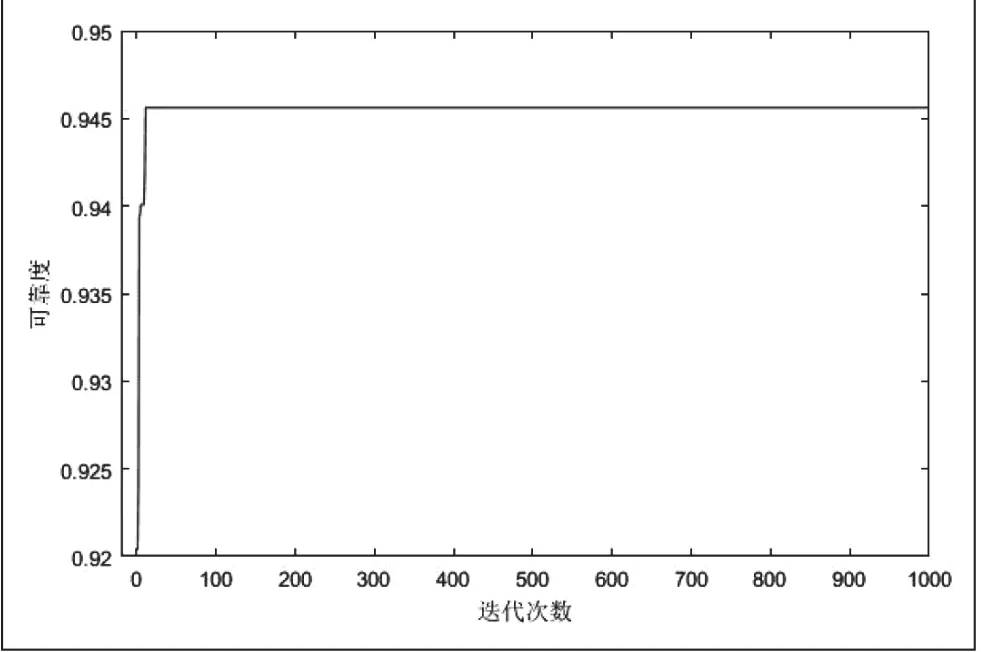
图3 算法3执行一次的收敛曲线

3.4 算法比较

将文献中求解2.3问题的算法运行结果列在了表3中，除第1个算法外，每种算法都随机的执行了50次。

表3 模型2实例算法求解结果汇总

从算法50次运行的平均结果看，HSO算法是几个算法中最好的；从算法执行的时间上看，HSO算法总的运行时间也是最短的，HSO算法的运行速率非常高；从算法收敛到最优解的次数上看，HSO算法也是比较好的。

4 结论

本文对两个较为简单的可靠性冗余分配问题模型，给出了具体的HSO算法，通过模拟仿真发现，HSO算法是求解RAP问题的有效工具。更具体的说，HSO求解模型二类型的问题，比PSO等算法，具有更好的优势，算法收敛速度快，平均解好；但求解模型一类型问题的时候，总体上看不比PSO等其它算法差多少，可是优势并不突出。因此，HSO算法比较适合解决多约束、规模较大的RAP问题。