基于EIS和神经网络的退役电池SOH快速估计

耿萌萌，范茂松，杨 凯，赵光金，谭 震，高 飞，张明杰

（1中国电力科学研究院有限公司，北京 100192；2国网河南省电力公司电力科学研究院，河南 郑州 450052）

近年来，在国家政策持续支持和动力电池技术不断进步情况下，我国电动汽车产业进入快速发展期，截止到2020年底，我国电动汽车保有量已接近500万辆。目前电动汽车采用的锂离子电池在使用过程中性能逐渐下降，当其不能满足车辆使用要求时，就要从电动汽车上退役下来，未来几年动力电池的退役量也将快速增加。在退役动力电池中，很多还具有较高的剩余容量(电池额定容量的70%～80%)，这些电池有可能应用于电网储能、通信基站备用等场景，实现动力电池的梯次利用。但由于动力电池退役时通常状态未知，因此在梯次利用前需要对其健康状态进行评估，来判断其能否梯次利用以及适用于哪种应用场景。

目前，锂离子电池健康状态的评估方法有定义法[1-3]、电化学阻抗法[4-5]、模型法[6-9]等。定义法最直接简单，在标准工况下，依据电池测试手册，对电池进行一次完全的充放电循环，放电容量与新电池的额定容量之比即为该电池当前状况下的SOH。该方法准确度高，但是时间成本高，且难以在实际工况中应用。但在研究阶段，可用此方法作为基准评价其他方法的估算准确度。

人工神经网络模型[10]无需建立方程，通过设计网络并对网络进行训练就可以处理锂离子电池SOH 与电池电压、电流和温度等参数之间的错综复杂的非线性关系。Sahar 等[11]提出了利用神经网络预测电池SOH 的方法，将非线性自回归的思想融入神经网络算法，研究了电池使用过程中容量衰减规律。但是此方法往往重数据而轻机理，导致估测方法普适性差。

电化学阻抗谱(electrochemical impedance spectroscopy，EIS)[12-15]可反映电池的很多电化学特征参数及相关反应的动力学信息。由于将电池的内部电化学反应机理考虑在内，通过这些参数来估计电池状态，结果更准确，但往往采用全谱测试并利用等效电路分析，有时间长、误差大的缺点。

为了开发在梯次利用过程中退役电池健康状态快速估计方法，本文在兼顾电池的电化学特性的同时，提取基于特定频率下实部、虚部等原始数据的特征参量，结合BP 神经网络模型可解决复杂非线性关系的优势，提出基于交流阻抗和BP 神经网络的退役电池健康状态快速估计方法，综合了EIS和BP 神经网络模型的优势，克服了电化学阻抗谱速度慢、解析复杂和BP 神经网络重数据不重机理的缺点。

1 实 验

1.1 样品

从某电动大巴车退役的方形磷酸铁锂(LiFePO4)电池，出厂额定容量为65 A·h。

1.2 循环实验

将退役磷酸铁锂电池单体置于25 ℃恒温箱中，利用深圳Neware 公司的CT-3008W 电池测试系统以0.5 C 倍率对其进行恒流充放电循环，充放电截止电压为2.5～3.65 V，每循环200 次计为1 个周期，标定容量。

1.3 电化学阻抗测试

利用电化学工作站(VMP3B，法国Bio-logic 公司)进行8只退役电池的电化学阻抗谱测试。8支退役电池在循环之前测试电化学阻抗，之后每循环一个周期测试一次50% SOC 下电化学阻抗，频率范围为10 kHz～10 mHz，激励电流为3 A。

2 特征参量选取

退役锂离子电池的健康状态一般定义为当前容量与额定容量的比值，见式(1)

式中，Qaged为电池在当前状态下的最大可用容量，A·h；Qnew为额定容量，A·h。

图1 为8 只退役磷酸铁锂电池在退役后的衰退曲线，从图中可以看到，随着循环周期的进行，放电容量基本呈线性衰减，经过11 个循环周期后，8只电池的放电容量在53～54 A·h之间。

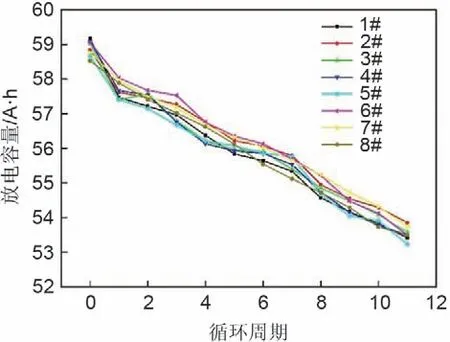
图1 退役磷酸铁锂电池的衰退曲线Fig.1 Decay curve of retired LiFePO4 batteries

在不同的循环周期对8只电池进行电化学阻抗测试，为了更加清晰地展示EIS随退役电池循环老化产生的变化，选取1#电池的第1、5、10 周期的50% SOC 时的交流阻抗谱图进行对比，如图2 所示，随着循环的进行，阻抗谱图沿着实轴(Z′轴)向右移动，说明EIS 随电池SOH 的不同是有规律性变化的，可用于电池SOH评估。

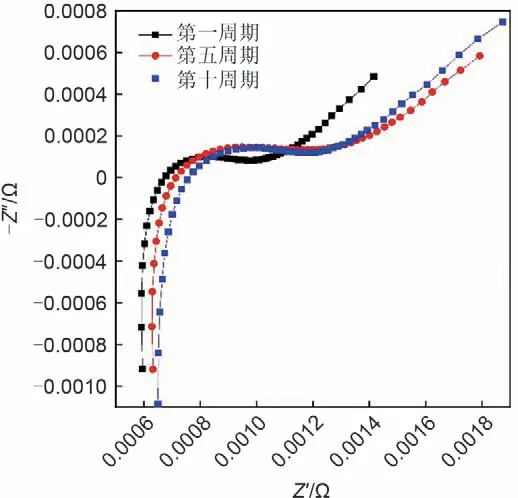
图2 不同循环周期的电化学阻抗谱Fig.2 EIS of different cycles

由图2 可以看出，锂离子电池的EIS 由高频区的一条垂直于实轴的直线、中频区的半圆以及低频区的一条与实轴45°夹角的直线构成，高频区的直线代表电感，主要由电池和电线里金属元素造成；与实轴相交的部分为欧姆阻抗，主要是正极材料、电解液、隔膜等阻抗之和；中频区的半圆主要是电极的双电层电阻和电荷转移电阻；低频区的直线代表在电极材料中的扩散电阻。通过分析锂离子电池的EIS 可知电池的内部反应，利用EIS 进行电池的SOH评估，可达到无损、准确的目的。

电化学阻抗法常规的分析方法是等效电路法，利用等效元件参数再进行SOH 评估，但是等效电路拟合的过程中存在误差，使估计误差更大，而且增加了时间和人工成本，不适合实际应用。由电化学阻抗原理可知，中频区的半圆与实轴相交的两点分别是(Rs，0)和(Rs+Rct，0)，其中Rs为欧姆内阻，Rct为电荷转移内阻，半圆的半径为Rct，所以选定EIS 与实轴相交处、半圆顶端及半圆与45°直线相交处的频率下的参数为特征参量。根据以上原则和实测数据，选定300 Hz、60 Hz、1 Hz三个频率下的原始数据作为特征参量，测试时间由十几分钟缩短至几秒钟，具体见表1。

表1 特征参量Table 1 Characteristic parameter

不同健康状态下退役电池的交流阻抗特征参量组成输入参量X= [X1,X2, …,Xn]，n为不同电池健康状态数量，其中Xn=[Z′300,Z″300, |Z|300,Z′60,Z″60,|Z|60,Z′1,Z″1, |Z|1]T，不同电池的健康状态为输出参量S=[S1,S2,…,Sn]。

本文直接利用EIS 原始数据特征参量，结合BP神经网络算法，快速评价电池SOH。

图3 为神经元模型，本文中以X为输入参量，见式(2)，对应在其箭头方向上的Wmn是权重系数，见式(3)，权重系数是为了消除样本数据的偏差，通常是一个Rand函数，在0～1之间的取值。将输入参量X和其对应的权重系数W的乘积的求和值输入神经元中，此时神经元得到了输入变量和其权重的乘积累加和，见式(4)和式(5)，通过映射函数F(x)来进行映射得到输出参量Y，即不同状态下锂离子电池的估测健康状态，见式(6)。以上就是一个简单的神经元模型和信息传递过程。

图3 神经元模型Fig.3 Neuron model

BP(back propagation)神经网络一般由输入层、隐含层以及输出层构成，BP 神经网络的学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，电池特征参量作为输入参数从输入层传入，经隐含层逐层处理后，传向输出层，得到估测健康状态Y。若Y与期望输出健康状态S不符，则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐含层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据。

3 模型训练和SOH估计

本文建立的BP神经网络模型包括一个输入层、一个隐含层、一个输出层，隐含层包括9 个节点，隐含层激活函数选择tansig函数，输出层的激活函数选择purelin 函数，损失函数选择MSE，学习速率为0.01，目标误差为5.0×10-5，最大迭代次数为1000。

3.1 数据预处理

对1#～8#不同循环周期下的交流阻抗谱数据进行预处理，筛选出300 Hz、60 Hz、1 Hz三个频率下实部、虚部、模值，对8只电池的不同循环周期的标定数据进行筛选，提取放电容量作为SOH的指标，之后为了加快学习速率，对所有提取的数据进行归一化处理，得到共96 组数据。通常情况下，数据量较大，训练样本和验证样本的比例大约为5∶5，而对于数据量较少的情况，训练样本和验证样本的比例一般在8∶2 或9∶1，以使得模型训练精度更高。不同循环周期下交流阻抗谱数据量较少，所以按照8∶2 分配数据，选择77 组数据用于训练，19 组数据用于模型验证，归一化公式见式(7)。

式中，x1为归一化后的数据；x为直接提取的数据；xmin为同组数据中的最小值；xmax为同组数据中的最大值。

3.2 模型训练和验证

模型训练过程如图4所示，归一化后的77组输入和输出参量及初始的权值和阈值，正向计算输出值误差，如果误差满足要求，则结束训练，模型即可进行SOH 估计，如果正向计算输出值误差不满足误差要求，则反向调整权值和阈值，直至满足优化条件为止。

图4 模型训练流程Fig.4 Model training flowchart

为了评价模型的准确性，采用平均绝对百分误差(mean absolute percentage error，MAPE)和均方根误差(root mean square error，RMSE)来评估模型训练和验证结果，MAPE和RMSE的表达式如式(8)、式(9)所示。

其中，Y为SOH估计值；S为实测SOH；N为预测总样本数。

退役磷酸铁锂电池的健康状态估算模型训练结果与实测结果的对比如图5 所示，训练数据在实测数据小范围内上下波动，整体来看，模型训练结果与实测结果的趋势基本一致，利用训练结果和实测结果计算MAPE 和RMSE，MAPE 为1.36%，RMSE为1.57%，说明模型训练结果整体误差较低。

图5 实测SOH和训练SOH的对比Fig.5 Comparison of measured SOH and training SOH

为了对训练的模型进行验证，采用19 组退役磷酸铁锂电池300 Hz、60 Hz 以及1 Hz 三个频率下的实部、虚部、模值为输入参量，对应的19 个SOH 值为输出参量的期望值，SOH 的估算值和实测值的对比如图6 所示，估算值在实测值附近波动，整体变化趋势与实测值也近似。通过计算，验证样本的估算值的MAPE 为1.46%，RMSE 为1.60%，和模型训练结果误差相当，说明模型未出现过拟合现象的同时，整体误差较低，估测精度较高。

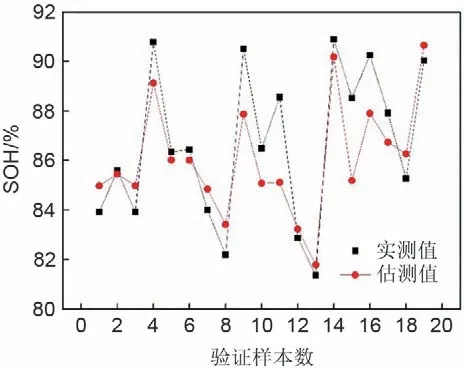
图6 容量实测值和验证估算值对比Fig.6 Comparison chart of capacity measured value and verified estimated value

4 结 论

本文基于电化学交流阻抗谱和BP 神经网络，建立了一种退役电池健康状态快速估计模型，综合了两种方法的优势，克服了电化学阻抗谱扫频全谱速度慢、解析复杂和BP 神经网络重数据不重机理的缺点，以电化学阻抗谱中300 Hz、60 Hz、1 Hz下的实部、虚部及模值为特征参量输入到搭建的BP 神经网络模型中，输出估计SOH，并利用MAPE和RMSE对退役电池健康状态快速估计模型的精确度进行评价，验证样本的MAPE 为1.46%，RMSE 为1.60%，和模型训练误差(MAPE 为1.36%，RMSE为1.57%)相当，说明模型未出现过拟合现象的同时，整体误差较低，估测精度较高。综上，基于EIS 和神经网络的退役电池SOH 快速估计方法测试时间短，估计结果精确度高，更有利于实际应用。