BeS分子基态与激发态势能函数和光谱性质的理论研究

项飞羽，令狐荣锋，吕 兵

(1.贵州师范大学 物理与电子科学学院，贵州 贵阳 550001；2.贵州工程应用技术学院，贵州 毕节 551700)

0 引言

分子势能函数和分子光谱性质是原子与分子物理学中一个重要的研究方向，它不仅是原子分子物理学和材料科学的重要基础[1]，而且是研究反应动力学的关键[2-4]。铍作为一种新兴材料日益被重视，是原子能、火箭、导弹、航空、宇宙航行以及冶金工业中不可缺少的宝贵材料。随着计算机科学和量子化学计算的进步，铍的化合物引起了人们的广泛关注。而BeS具有良好的热传导性，高熔点和强韧性[10]，是人们比较感兴趣的陶瓷制品和荧光材料，目前，BeS在高压下的相变和有关物理性质已引起科学工作者的广泛关注[5,6]。

本文利用原子分子反应静力学的原理[1,7]，推导出了BeS分子基态X1Σ+，第一简并激发态A1Π和第二激发态B1Σ+的离解极限，利用SAC/SAC-CI方法结合D95++，6-311++G，6-311++G**，CC-PVDZ这4个基组[11-12]，分别对BeS分子的X1Σ+，A1Π和B1Σ+态进行几何优化，从中优选出6-311++G**基组，用SAC方法对基态，SAC-CI方法对激发态进行单点能扫描，且拟合出Murrell-Sorbie函数，并计算出各阶力常数和光谱常数[13-17]，用SAC-CI方法理论计算的结果与实验数据[8]非常吻合。

1 理论计算

1.1 BeS分子的离解极限

BeS分子为线性双原子分子，属C∞V群。要获得其基态X1Σ+，第一简并激发态A1Π和第二激发态B1Σ+的正确势能函数，必须确定其合理的离解极限[9]。 Be原子的基态为1Sg，S原子的基态为3Pg；Be原子的激发态为3Pu，S原子的激发态为1Dg，它们都属于SO(3)群。根据wigner-witmer规则和群的直积约化理论可以得到：

Be+S→BeS

1Sg+3Pg3Σ-,3Π

(1)

1Sg+1Dg1Σ+,1Π,1Δ

(2)

3Pu+3Pg1,3,5Σ+,21,3,5Σ-,21,3,5Π,1,3,5Δ

(3)

3Pu+1Dg23Σ+,3Σ-,33Π,23Δ+2φ

(4)

可以看出，只有过程(2)和(3)才含有我们需要的1Σ+和1Π态，根据微观过程可逆性原理。即若正过程发生，则逆过程也可以发生，所以X1Σ+态的离解极限可能：

BeS(X1Σ+)→Be(1Sg)+S(1Dg)

(5)

BeS(X1Σ+)→Be(3Pu)+S(3Pg)

(6)

A1Π态的离解极限可能有：

BeS(A1Π)→Be(1Sg)+ S(1Dg)

(7)

BeS(A1Π)→Be(3Pu)+S(3Pg)

(8)

B1Σ+态的离解极限可能有：

BeS(B1Σ+)→Be(1Sg)+S(1Dg)

(9)

BeS(B1Σ+)→Be(3Pu)+S(3Pg)

(10)

又由表1所列的Be原子和S原子的光谱数据可以知道，对于X1Σ+态，通道(5)的能量最小，对于A1Π态，是通道(7)的能量最小，当X1Σ+态占据通道(5)时，B1Σ+态只能通过通道(10)离解才合理，所以根据能量最小优先原则，X1Σ+态、A1Π态、B1Σ+态的合理离解极限为：

BeS(X1Σ+)→Be(1Sg)+S(1Dg)

(11)

BeS(A1Π)→Be(1Sg)+ S(1Dg)

(12)

BeS(B1Σ+)→Be(3Pu)+ S (3Pg)

(13)

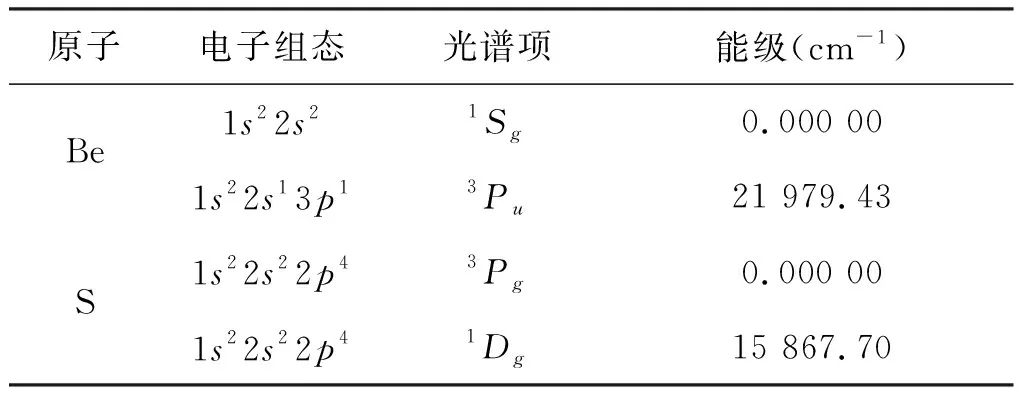
表1 Be原子和S原子的光谱数据Tab.1 Spectrum data of Be and S atoms

1.2 BeS分子基态和激发态的结构参数

本文分别选用D95++，6-311++G，6-311++G**，CC-PVDZ等4个基组，分别对BeS分子的X1Σ+态、A1Π态、B1Σ+态分别进行几何优化，表2列出了本文部分较好的计算结果，Re和Te分别为平衡位置的核间距和绝热激发能，对于Re和Te表中也列出了文献报导的实验结果。由表2可以看出6-311++G**基组计算得到的平衡核间距Re和Te与实验值符合很好。因此，本文后面对BeS分子的基态和激发态的单点能扫描都使用6-311++G**基组进行计算。

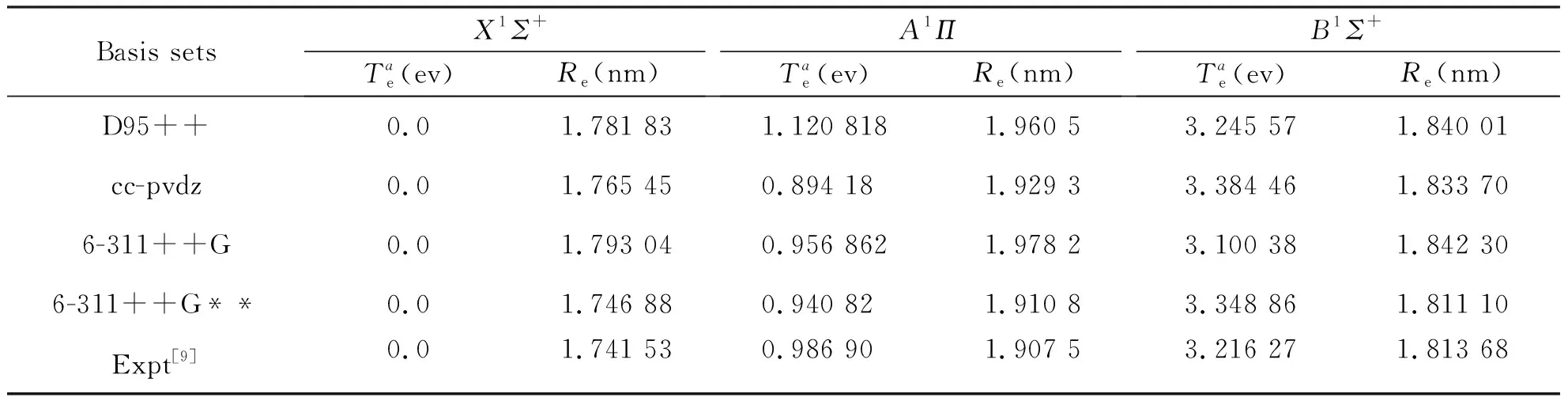
表2 BeS分子的X1Σ+，A1Π和B1Σ+态的优化计算结果Tab.2 Optimization calculation of three electronic states X1Σ+, A1Π and B1Σ+ of BeS molecules

1.3 BeS分子基态和激发态的势能函数及光谱常数的计算

根据图1，可以得到：

(14)

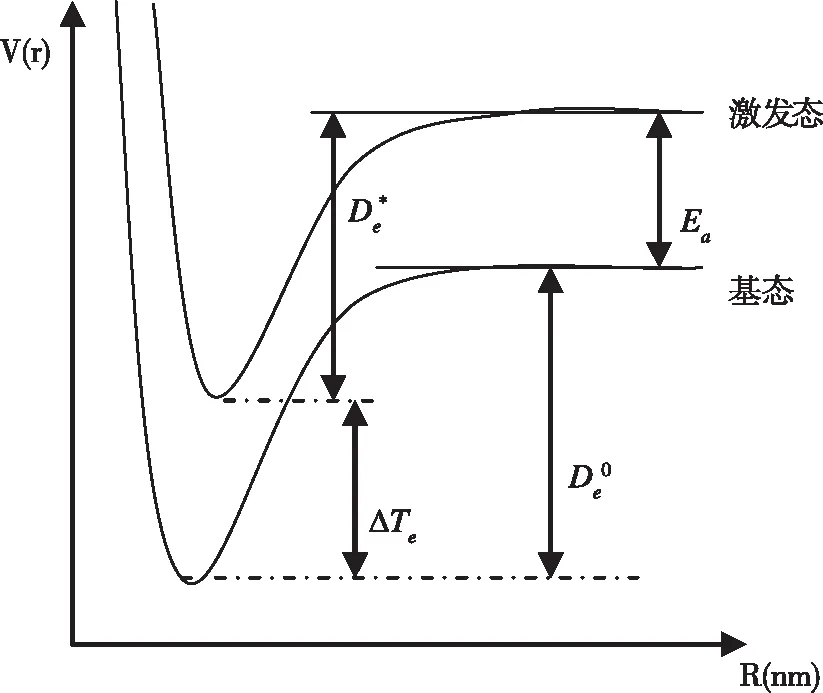
图1 基态与激发态势能曲线图Fig.1 Curve of ground state and excitation

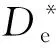
(15)

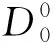
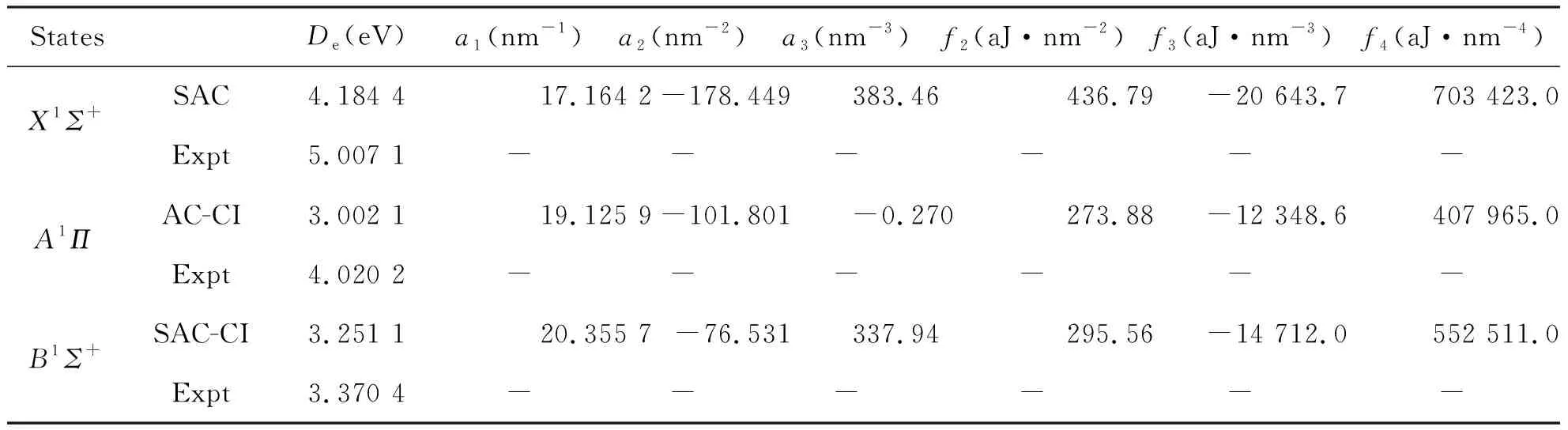
表3 BeS分子的X1Σ+，A1Π和B1Σ+态的 Murrell-sorbie 势能函数Tab.3 Murrell-sorbie potential energy function of three electronic states X1Σ+, A1Π and B1Σ+ of BeS molecules

图2给出了BeS分子的基态X1Σ+，第一简并激发态A1Π和第二激发态B1Σ+的势能曲线。其中，线为拟合得到的Murrell-Sorbie函数势能曲线，圆圈为单点能扫描的结果。由图2可以看出，本文扫描计算得到的基态X1Σ+，第一简并激发态A1Π和第二激发态B1Σ+态离解能，与拟合得到的结果一致，其它位置的点、线间也吻合得很好。这说明拟合出的Murrell-Sorbie函数确实能正确表达BeS分子的基态X1Σ+，第一简并激发态A1Π及第二激发态B1Σ+的势能函数。

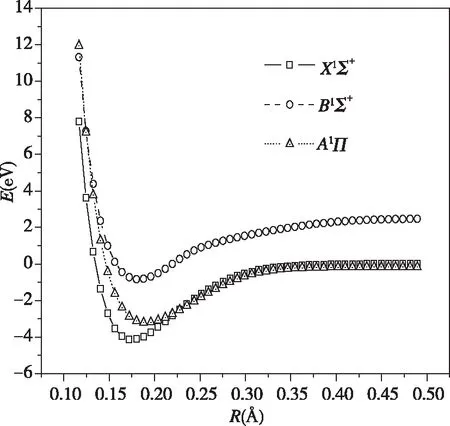
图2 BeS基态和低激发态的势能曲线Fig.2 Potential energy curves of BeS ground state and low excited state

根据力常数与光谱常数的关系，可计算出BeS基态和激发态的光谱常数ωe、ωeχe、Be、αe。计算结果列于表4。由表4可以看出，利用标准的Murrell-Sorbie函数拟合BeS分子基态，第一简并激发态和第二激发态得到的参数计算所得光谱常数与实验结果吻合很好。

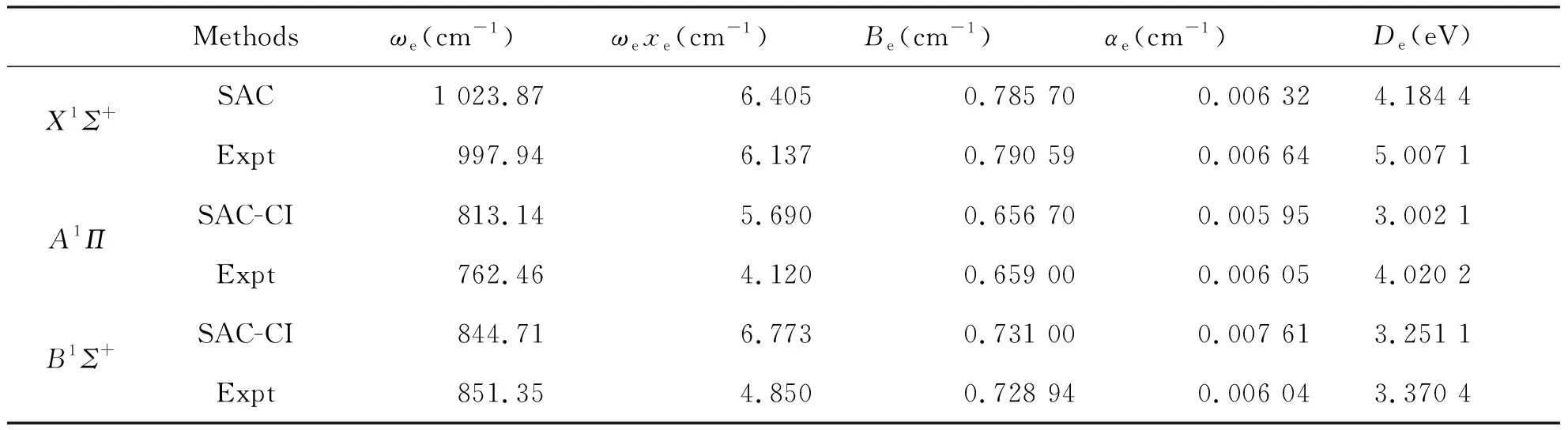
表4 BeS分子X1Σ+，A1Π和B1Σ+态光谱常数Tab.4 Spectrum data of three electronic states X1Σ+, A1Π and B1Σ+ of BeS molecules

2 结论

本文利用SAC/SAC-CI方法结合D95++，6-311++G，6-311++G**，CC-PVDZ这4个基组，分别对BeS分子的X1Σ+，A1Π和B1Σ+态进行几何优化，从中优选出6-311++G**基组，用SAC方法对基态，SAC-CI方法对激发态进行单点能扫描，且拟合出Murrell-Sorbie函数，计算结果与实验光谱数据比较吻合。这表明，用SAC-CI方法理论计算的结果，并用Murrell-sorbie来显示，能正确的描述BeS分子的基态，第一简并激发态和第二激发态的势能函数与光谱性质。