用φ(ξ)展式法求非线性演化方程的行波解
2022-02-18林府标
王 骞,林府标
(1.贵州师范大学 附属中学,贵州 贵阳 550001;2.贵州财经大学 数学与统计学院,贵州 贵阳 550025)
0 引言
受数学机械化[1]思想的启发,研究非线性演化偏微分方程[2-4]的方法与技巧不断涌现。此类方程本身的物理背景和行波解的特殊性质,使得其精确求解及行波理论已成为非线性科学关注的前沿和热点问题之一。随着数学机械化的应用和计算机的更新与发展,方程的精确解的解法研究分支中呈现出各种代数方法,如拟设法[3]、广义tanh函数法[4-5]、ψ(ξ)展式法[6]、广义正余弦函数法[7-8]、齐次平衡法[9]、符号计算的代数法[10]、1/G-展开法[11]、Jacobi椭圆函数展开法[12]、tanh函数法[4,13]等。这些方法和技术既丰富了非线性演化方程的研究内容,又为精确求解的机械化及探究更多新的行波解找到了突破口和方向。因此,继续探索、研究、挖掘、构造及创新这些方法是有实际价值和研究意义的。
在前人的工作和文献[5-8]的基础之上,该文研究精确求解非线性演化偏微分方程的4种φ(ξ)展式法,用这些方法分别探究七阶SK-Ito方程、五阶KdV方程、三阶KdV方程、三阶Joseph-Egri方程的新行波解。
1 一阶常微分方程及精确解
1.1 标准Riccati方程
Riccati方程φ′(ξ)=η(ξ)+ω(ξ)φ(ξ)+r(ξ)φ2(ξ),r(ξ)≠0在微分方程的经典理论、近代科学的有关分支领域、解析求非线性演化偏微分方程的行波解、广义tanh函数法、符号计算机械化的代数方法等方面,均有重要应用[4-5]。文献[5]给出标准Riccati方程
(1)
的8种类型的精确解,其结果列于表1,其中b为实常数,可用于确定行波解的形状和数量。

表1 Riccati方程(1)的显式精确解, 其中ε=±1,a1,a2为常数Tab.1 Explicit exact solutions of the Riccati equation (1), where ε=±1,a1,a2 are constants
1.2 Liouville方程的约化方程
Liouville方程uxt=exp(u)是一个常用于流体力学的非线性偏微分方程,其精确求解的方法与技巧在非线性科学中,受到学者们的关注和重视[4,6]。在前人工作和文献[6]的基础上,给出Liouville方程的约化方程
(2)
的6种类型的精确解,其中ε=±1,κ,c为实常数,其结果列于表2,序号是4和5及6的精确解文献[6]未给出。

表2 方程(2)的显式新精确解, 其中ε=±1,a1,a2为常数Tab.2 Explicit new exact solutions of equation (2), where ε=±1,a1,a2 are constants
1.3 sin-Gordon方程的约化方程
非线性波动sin-Gordon方程uxt=sinu在孤立子理论、孤波现象、晶体位错、磁学、光学、生物系统、超导体等学科分支领域有广泛的应用,解析求行波解的各种方法异军突起[4,7]。受前人工作的启发及在文献[7]的基础上,给出sin-Gordon方程的约化方程
(3)
的4种类型的精确解,其中ε=±1,κ,c为实常数,其结果列于表3,序号为3和4的精确解,文献[7]均未给出。
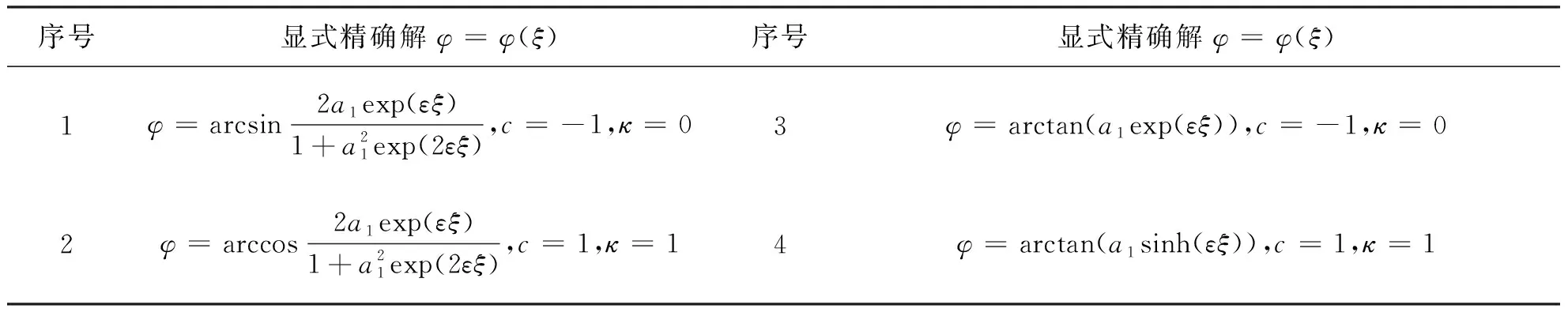
表3 方程(3)的显式新精确解, 其中ε=±1,a1,κ为常数Tab.3 Explicit new exact solutions of equation (3), where ε=±1,a1,κ are constants
1.4 双sin-Gordon方程的约化方程
不可积的双sin-Gordon方程uxt=sinu+sin(2u),在生物蛋白质分子理论、物理学、孤立子理论、工程科学等分支领域有广泛的应用,其孤立波之间的相互作用是非弹性的,探寻行波解及孤立波解的方法和技巧[4,8]。受前人工作的启发和在文献[8]的基础上,给出双sin-Gordon方程的约化方程
(4)
的4种类型的精确解,其中ε=±1,κ,c为实常数,其结果列于表4。
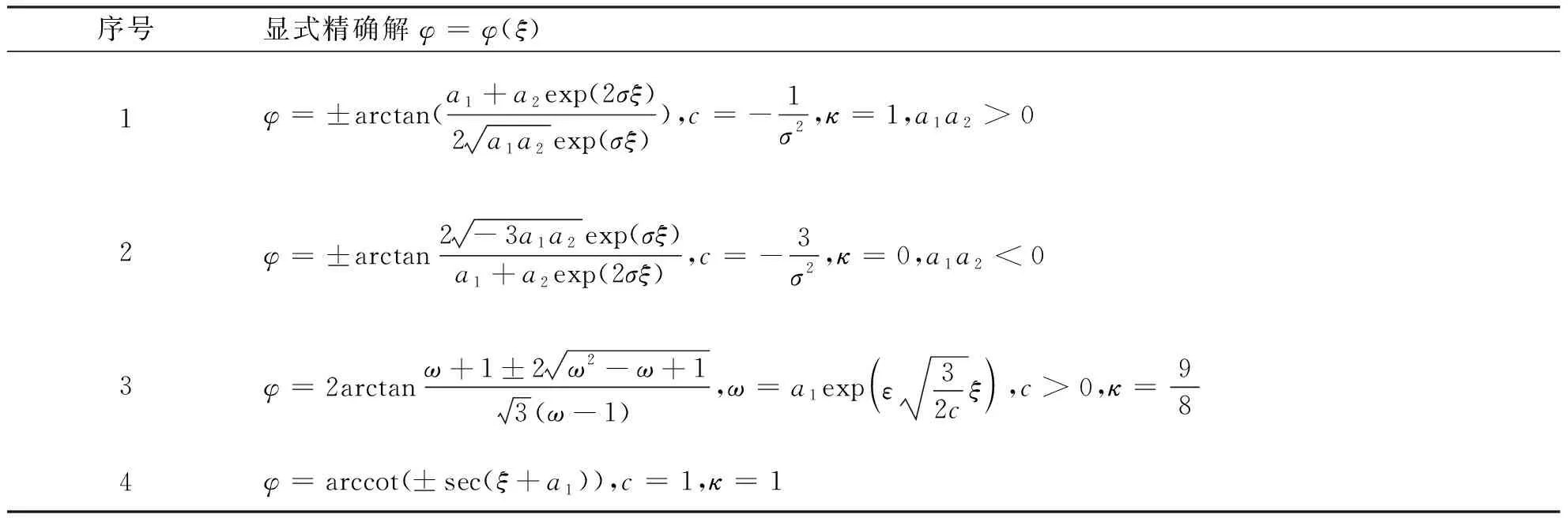
表4 方程(4)的显式精确解, 其中ε=±1,κ,c,a1,a2,σ为常数Tab.4 Explicit exact solutions of equation (4), where ε=±1,κ,c,a1,a2,σ are constants
2 φ(ξ)展式法
受前人工作的启发[1-4]和在文献[5-8]的基础上,用(1)~(4)式,构造解析求非线性演化偏微分方程
P(u,ut,ux,utt,uxx,uxt,…)=0
(5)
的行波解的φ(ξ)展式法, 其中,P代表含u和u的各阶偏导数的多项式。
φ(ξ)展式法的基本思想和主要步骤:
1)设u(x,t)=U(ξ),ξ=x-ct是(5)式的解,其中c为常数,代表波速,则(5)式转化为
P(U,-cU′,U′,c2U″,U″,-cU″,…)=0
(6)
2)对某些高阶常微分方程(6),若可降阶,可考虑首先积分一次或多次,再设解可写成
U(ξ)=x0+x1φ(ξ)+x2(φ(ξ))2+…+xn(φ(ξ))n
(7)
其中,φ=φ(ξ)满足(1)式或(2)式。若解假设为
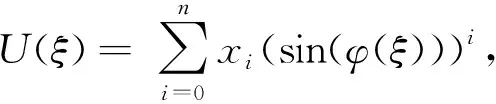
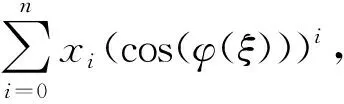
(8)
其中,φ=φ(ξ)满足(3)式或(4)式,xi(i=0,…,n)为待定实参数,正整数n可依据齐次平衡原理[4,9],由(6)式中非线性项与最高阶导数项平衡而获得。
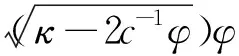
4)将解xi(i=0,…,n)代入(7)式或(8)式,依据b,κ的值及符号,选取表1~表4中相应的φ=φ(ξ),从而可写出方程(5)的行波解及表达式。
3 φ(ξ)展式法的应用
3.1 七阶SK-Ito方程的行波解
七阶SK-Ito方程[10]
(9)
可用于研究物理学领域的波理论、孤立子理论、波的色散问题等。
设方程(9)的解为u(x,t)=U(ξ),ξ=x-ct,其中c为常数,代表波速,于是得到
252U3U′+63(U′)3+378UU′U″+126U2U‴+63U″U‴+42U′U(4)+21UU(5)+U(7)-cU′=0
(10)
依据(1)式和齐次平衡原理,由(10)式中U(7)与U3U′项平衡,得n=2。因此,设(10)式的解可写成
U(ξ)=b0+b1φ(ξ)+b2(φ(ξ))2
(11)
其中,b0,b1,b2是待定的实参数,φ=φ(ξ)满足(1)式,将(11)式代入(10)式,得
令φi(i=0,…,9)的系数为零,得关于b0,b1,b2,b,c的方程组,用吴消元法,解得
因此,方程(9)的行波解为
(12)
(13)
其中,φ=φ(ξ)可依据b的符号从表1中选取,为行文简洁,仅将解(13)列于表5,类似可写出解(12),解(12)和(13)文献[10]未给出。

表5 SK-Ito方程(9)的显式行波解, 其中ε=±1,a1,a2为常数Tab.5 Travelling wave solutions of SK-Ito equation (9), where ε=±1,a1,a2 are constants
3.2 五阶KdV方程的行波解
五阶KdV方程[10-11]
ut+αu2ux+βuxu2x+γuuxxx+uxxxxx=0
(14)
可用于研究等离子体、磁声传播、物理学波理论等,其中α,β,γ是非零常数。若取α=30,β=20,γ=10,方程(14)变成Lax方程;若取α=5,β=5,γ=5,方程(14)变成SK方程;若取α=20,β=25,γ=10,方程(14)变成KK方程;若取α=2,β=6,γ=3,方程(14)变成Ito方程。
设方程(14)的解为u(x,t)=U(ξ),ξ=x-ct,其中c为常数,代表波速,则得到
αU2U′+βU′U″+γUU‴+U(5)-cU′=0
(15)
根据(2)式及齐次平衡原理,由(15)式中U(5)与U2U′项平衡,得n=1。因此,设(15)式的解可写成
U(ξ)=d0+d1φ(ξ)
(16)
其中,d0,d1是待定的实参数,φ=φ(ξ)满足(2)式,把(16)式代入(15)式,得

2αcd0d1+βcd1κ+cd1γκ-6d0γ-30κ=0。
1)情形:α=30,β=20,γ=10,解得
因此,Lax方程(14)的行波解为
其中,φ=φ(ξ)可依据κ的符号从表2中选取,为了行文简洁,省略具体列举过程。
2)情形:α=5,β=5,γ=5,解得
因此,SK方程(14)的行波解为
其中,φ=φ(ξ)可根据κ的符号从表2中选取,为了行文简洁,省略具体列举过程。
3)情形:α=20,β=25,γ=10,解得
因此,KK方程(14)的行波解为
其中,φ=φ(ξ)可依据κ的符号从表2中选取,为了行文简洁,省略具体列举过程。
4)情形:α=2,β=6,γ=3,解得
因此,Ito方程(14)的行波解为
其中,φ=φ(ξ)可依据κ的符号从表2中选取,为了行文简洁,省略具体列举过程。情形1)~4)找到的解文献[10-11]未给出。
3.3 三阶 KdV方程的行波解
三阶非线性数学物理KdV方程[3-4,10,12]
ut+βuux+γuxxx=0
(17)
在孤立子理论学、流体动力学等分支领域有广阔的应用,其中β,γ是常数。
设方程(17)的解为u(x,t)=U(ξ),ξ=x-ct,其中c为常数,代表波速,则得到
βUU′+γU‴-cU′=0
(18)
依据(3)式和齐次平衡原理,由(18)式中U‴与UU′项平衡,得到n=2。因此,设(18)式的解可写成
U(ξ)=p0+p1cos(φ(ξ))+p2cos2(φ(ξ))
(19)
或
U(ξ)=p0+p1sin(φ(ξ))+p2sin2(φ(ξ))
(20)
其中,p0,p1,p2是待定的实参数,φ=φ(ξ)满足(3)式,将(19)式代入(18)式,得
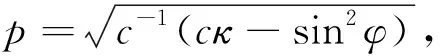
类似地,用(20)式求解,可解得
因此,方程(17)的行波解为
ξ=x-ct,
ξ=x-ct,
其中,φ=φ(ξ)可依据κ的值从表3中选取,为了行文简洁,省略具体列举过程,这些解文献[3-4,10,12]未给出。
3.4 Joseph-Egri方程的行波解
动力学数学物理Joseph-Egri方程[3-4,13]
ut+ux+βu2ux+γuttx=0
(21)
可用于非色散冲击波的分散模拟,其中β,γ是常数。
设方程(21)的解为u(x,t)=U(ξ),ξ=x-ct,其中c为常数,代表波速,于是得到
U′-cU′+βU2U′+c2γU‴=0
(22)
依据(4)式和齐次平衡原理,由(22)式中U‴与U2U′项平衡,得到n=1。因此,设(22)式的解可写成
U(ξ)=q0+q1tan(φ(ξ))
(23)
其中,q0,q1是待定的实参数,φ=φ(ξ)满足(4)式,把(23)式代入(22)式,得
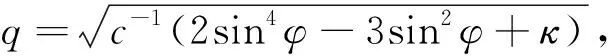
qcos2φ,qcosφsinφ,q的系数均为零,解得
因此,方程(21)的行波解为
其中,φ=φ(ξ)可依据κ的值从表4中选取,为了行文简洁,省略具体列举过程,这些解文献[3-4,13]未给出。
4 结束语
该文是在文献[5-8]的基础上,增加了方程(2)和方程(3)的新精确解,拓展了用φ(ξ)展式法解析求一些非线性演化偏微分方程的行波解的数量,丰富了精确解的类型及多样性。这些方法和技巧可用于求解其它一些非线性演化偏微分方程的新行波解,如Burgers方程ut+uux-uxx=0。Kuramoto-Sivashinsky方程ut+uux+αuxx+βuxxxx=0,其中,α,β为常数。耦合三阶KdV方程ut+6uux-6vvx+uxxx=0,vt+3uvx+vxxx=0等。今后的研究工作中还可继续考虑方程(1)~方程(4)的更多类型的新显式精确解。
