最概然分布的少粒子修正是必要的吗？

侯吉旋

(东南大学 物理学院，江苏 南京 211189)

对于处于平衡态的孤立系统，微观状态最多的分布称为最概然分布.由于最概然分布所包含的微观状态数远多于其他分布所包含的微观状态数，于是可以通过计算最概然分布来求得系统的平衡态性质，这种方法称为最概然近似.一般统计物理教材在推导平衡态分布(包括玻耳兹曼分布、玻色分布和费米分布)的时候都要用到斯特令近似[1,2]：

lnn!≈nlnn-n

(1)

尽管利用最概然近似求平衡态分布的推导过程较简单，但存在极大的缺陷.因为系统中能级l上的粒子数al很可能不满足斯特令近似的要求，粒子数al甚至可能远小于1，强行使用斯特令近似在数学上无法自圆其说.例如若要经典玻耳兹曼统计适用于稀薄气体，必须保证稀薄性假设(al<<ωl)[2]，其中ωl为能级l的简并度.文献[2]做了估计，氦气在标准状态下al/ωl≈4×10-6, 这已远超出式(1)适用范围.

有不少学者尝试使用精度更高的斯特令公式

(2)

来重新推导平衡态分布，以期得到在少粒子条件下更贴近实验测量的结果[3,4].文献[3]指出，若系统的粒子数少于100，少粒子修正将使得系统的热容量发生十分显著的变化.尽管利用斯特令近似式(1)的推导存在缺陷，但也有学者认为教材中原本得到的平衡态分布就是精确的，用精度更高的的斯特令公式(2)去推导是不必要而且错误的[5].

随着纳米技术的发展，少粒子系统越来越得到科学界与工业界的重视.统计物理中的平衡态分布是否需要进行少粒子修正将是人们不得不面对的问题.为了回答这个问题，本文将利用一个统计物理中严格可解的系统——一维谐振子势阱中的理想玻色气体，在无近似的情况下计算其基态布居数.再使用2种最概然近似(无修正与少粒子修正)计算其基态布居数，对比各种方法得到的结果即可做出基本的判断.

1 平衡分布及其少粒子修正

考虑一个包含N个非定域粒子的总能量为E的孤立系统，以εl(l=0,1,2,…)表示粒子的能级，ωl表示能级εl的简并度，al为能级εl上的布居数.那么对于经典粒子构成的系统、玻色系统和费米系统，其微观状态数分别为

(3)

(4)

(5)

为简单起见，下文省略微观状态数的下脚标.

下面列出求解最概然分布的要点，详细推导见文献[1-4].要得到最概然分布，可求lnΩ的极大值，即在粒子布居数al有虚变动δal时δlnΩ=0.注意到对于孤立系统δal不是完全独立的，必须满足条件：

N-∑lal=0

(6)

E-∑lεlal=0

(7)

于是最概然分布满足条件极值：

δ[lnΩ+α(N-∑lal)+β(E-∑lεlal)]=0

(8)

其中α和β为2个拉格朗日乘子.

本文考虑少粒子修正，即依然假设ωl>>1, 但是al不满足远大于1的要求.由于Ω中含有al的阶乘，需要对

(9)

进行化简.式(9)中μ=0或1.μ=0表示未考虑少粒子修正，而μ=1表示进行了少粒子修正.将式(3)—式(5)式代入式(8)求解，可得到最概然近似下各种平衡态分布：

(10)

其中θ=0对应于经典粒子构成的系统，即玻耳兹曼分布；θ=-1对应于玻色系统，即玻色分布；θ=+1对应于费米系统，即费米分布.玻耳兹曼分布呈现e指数分布是使用了斯特令近似的结果[2].μ=0时式(10)退回到常见的最概然分布公式.而μ=1时式(10)对于al而言仅为形式解，使用时需要数值求解超越方程才能得到al的数值.而拉格朗日乘子α和β则由条件式(6)和(7)来确定.

2 一维谐振子势阱中的理想玻色气体

为了检验少粒子修正的必要性，本文将利用一个在微正则系综中可以严格求解的系统，即一维谐振子势阱中的理想玻色系统[6-8].设谐振子势阱的能级间距为ε, 并取基态能级为能量零点.由于一维谐振子系统无简并，设有nl个玻色子占据第l个能级，那么该系统中各能级上粒子数满足

(11)

其中m≡E/ε为元激发的个数.满足式(11)的一组非负整数解{n0,n1,…,nl,…}就对应于系统的一个微观状态.因此满足式(11)的非负整数解的个数，就是该系统的总的微观状态数.

若系统的能量较低，满足m≤N时，求解该系统的微观状态数等价于正整数拆分问题.用p(m)表示整数m的无限制正整数拆分方式的种数.例如m=3≤N, 对m有3种拆分方式，即p(3)=3, 分别为m=3,m=2+1以及m=1+1+1.这3种拆分方式对应于系统的3种微观状态，分别为{N-1,0,0,1,0,…}, {N-2,1,1,0,0,…}和{N-3,3,0,0,0,…}.

若系统的能量较高m>N, 受到粒子数目的限制，此时的拆分方式个数pN(m)显然要小于p(m).以m=3而N=2为例，对m的拆分就只有m=3和m=2+1两种, 即p2(3)=2.对应于系统的2种微观状态，分别为{1,0,0,1,0,…}和{0,1,1,0,0,…}.图1中画出了p(m)与p10(m)的前100个值，可见当m较小时pN(m)≈p(m).

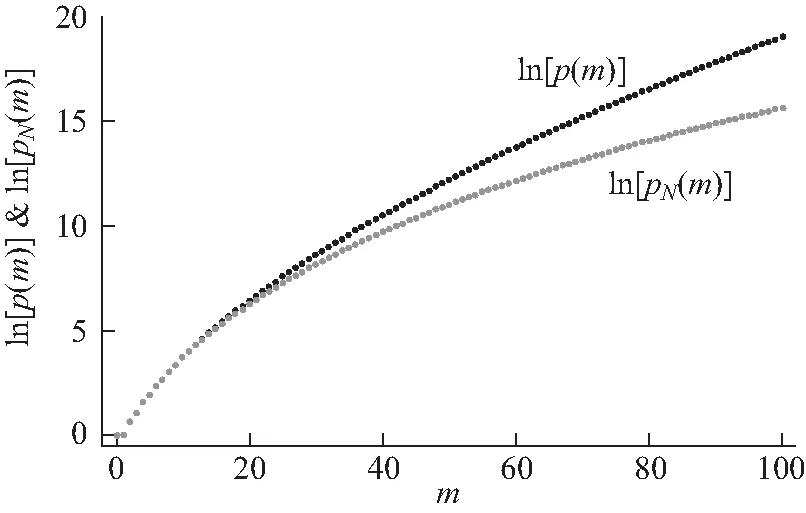
图1 N=10拆分数p(m)与pN(m)

由于已经得到了系统的微观状态数Ω(m,N)=pN(m), 便可以求得系统的熵：

S=kBln[Ω(m,N)]=kBln[pN(m)]

(12)

其中kB为玻耳兹曼常量.

3 谐振子势阱中玻色气体的基态布居数

一维谐振子势阱中理想玻色气体的平均基态布居数a0=〈n0〉,首先是由Grossmann等人[6]于1996年求得的，其中〈…〉表示系综平均.而后本文作者采用了另一种更加简单的方法得到了一致的结果[7].为了叙述方便，本文采用后一种方法.

假设已知系统的基态上有n0个玻色子，需要求得在这种条件下的系统的微观状态数.以N=6,m=6并且固定基态上有且仅有3个玻色子(n0=3)为例.如图2(a)所示，系统只有3种可能的微观状态.在图2(a)中，若隐去基态，同时将第一激发态重新标定为新的基态，将得到图2(b)所示的情况，刚好等价于N=3且m=3时的状况.

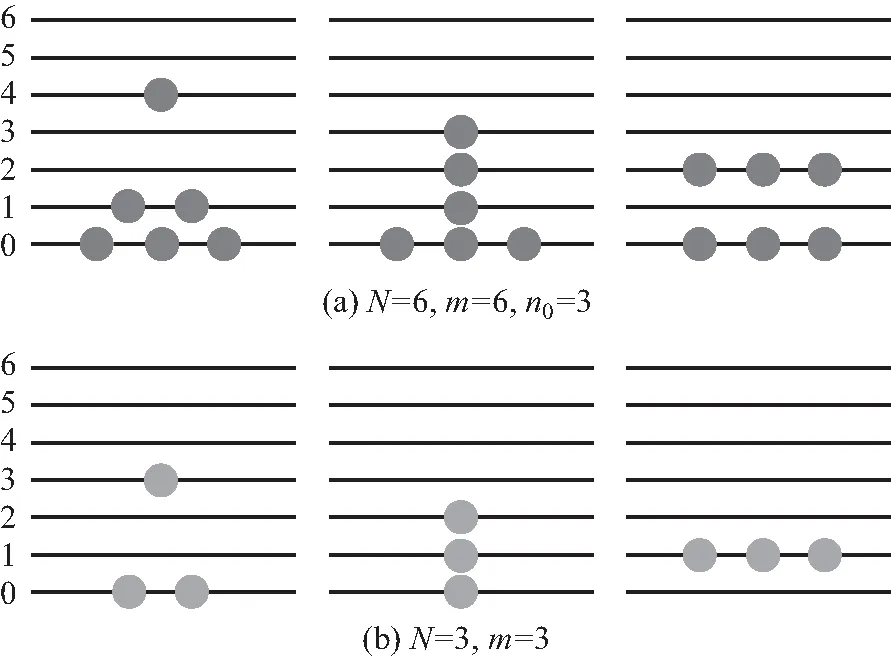
图2 玻色微观状态示意图

从数学上看，式(11)可以变形为

(13)

式(11)和式(13)在数学上是等价的，但是在给定n0后，式(13)的非负整数解的个数变为pN-n0(m-N+n0).也就是说，在给定基态上有n0个玻色子的条件下，系统的微观状态数为Ω(m,N|n0)=pN-n0(m-N+n0), 这可以从图2给的例子中看出.很显然，将基态取各种n0值时的微观状态数Ω(m,N|n0)相加就等于不指定基态占有数时候的总的微观状态数Ω(m,N), 即

Ω(m,N)=∑n0Ω(m,N|n0)

(14)

根据以上讨论可知，基态上有n0个玻色子的统计权重w0(n0)为

(15)

在图3中，以N=10为例，给出了系统取不同m值时的基态粒子数的统计权重.得到n0的统计权重后，可进一步求得平均基态布居数：

a0=〈n0〉=∑n′0n′0·w0(n′0)

(16)

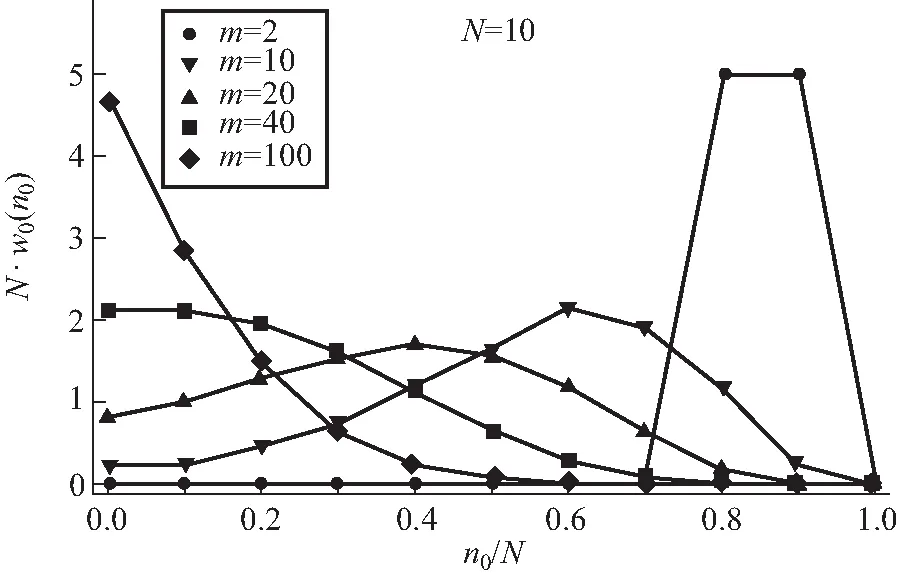
图3 给定m后基态上有n0个玻色子的统计权重w0

4 基态布居数的对比

在上一节中，给出了计算一维谐振子势阱中的理想玻色系统的基态布居数的方法.该方法未使用最概然近似，因此是严格的结果.

另一方面，要使用最概然近似，则需要联立式(6)、式(7)和式(10)进行数值求解，在粒子数N很大的时候极为消耗计算机的算力.但是好在少粒子修正只在N较小时才显得重要，于是本文仅数值求解了N=10和20两种情况，其结果显示在图4中.注意，由于处理的是玻色系统，式(10)中的θ应取-1.

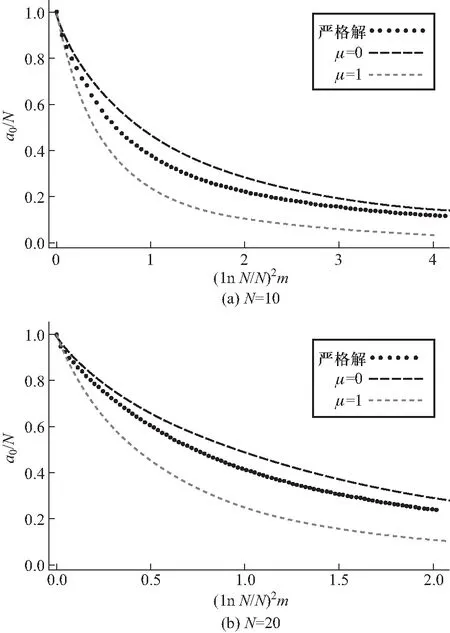
图4 基态布居数a0随系统能量m的变化

图4对比了用不同方法求得的基态布居数a0随系统的能量m的变化曲线.图中点为上一节中介绍的用数论给出的严格解，而虚线给出的是用最概然近似求出的结果.长虚线表示的是没有少粒子修正的结果(μ=0)，而短虚线表示的是采用少粒子修正之后的结果(μ=1).文献[6]指出，一维谐振子势阱中的理想玻色系统有一个特征能量，m*～(N/lnN)2.系统能量低于m*时，基态上的粒子数将与总粒子数是同一个数量级，即a0=O(N).为了让不同粒子数的系统具有可比性，在作图4时，重新标度了坐标，横坐标取m/m*, 纵坐标取a0/N.

从图4中可以看到，未修正的最概然近似结果与严格解是比较接近的，但是经过少粒子修正的最概然近似结果却与严格解偏差较大，这与人们初始的预期是相背离的.因为进行少粒子修正的目的就是让计算结果与严格解更加贴合.由此同意文献[5]的判断，在计算最概然分布时使用少粒子修正是不必要的.

5 结论

一般教材中推导最概然分布时采取的数学处理存在数学上的漏洞，在粒子数较少时是无法自圆其说的.于是很多研究人员尝试使用精度更高的斯特令公式重新推导，给出少粒子修正以弥补这一漏洞.本文计算了一维谐振子势阱中的理想玻色气体，发现不使用少粒子修正的最概然分布计算得到的基态布居数与严格解偏差较小，而使用少粒子数修正后的最概然近似计算得到的结果与严格解偏差甚大.于是我们认为，推导最概然分布时使用少粒子修正是不必要的.