博饼游戏中骰子投掷次数的概率分布与数学期望
2022-02-18储理才
储理才
(集美大学理学院,福建 厦门 361021)
0 引言
游戏从一开始就伴随着人类文明的发展史,最简单的游戏中都可能蕴含着基本的数学原理[1-2]。从最原始的赌博游戏到现在各种复杂的电脑手机游戏,游戏的持续时间一直是人们关注的焦点。对于游戏的持续时间现在已发展了一系列研究方法,如马尔科夫链方法[3]、鞅方法[4]等。
中秋博饼是流行于闽南厦漳泉以及台湾、东南亚地区的一项民俗活动[5]。传统的“博饼”活动设有大小不同、形态各异的月饼作为奖品,分为6个等级,由高到低分别设“状元”1 个、“对堂”2 个、“三红”4 个、“四进”8 个、“二举”16 个、“一秀”32 个。全套月饼共 63 块,称为“会饼”。当前在闽南地区比较通用的获奖规则如下:1)状元,6枚骰子中出现 5 个以上相同点数或有 4 个以上为 4 点;2)对堂,6枚骰子的点数恰好为 1,2,3,4,5,6;3)三红,6枚骰子 中出现 3 个 4 点;4)四进,6枚骰子中出现 4 个相同的不为 4 的点数;5)二举,6枚骰子中出现 2 个 4 点;6)一秀,6枚骰子中出现 1 个 4 点;7)罚黑,若结果不符合以上任何一个条 件,则称为罚黑,不取得任何奖品。获奖等级采取就高不就低原则。根据以上规则,可以计算出各个等级的获奖概率[6-8],即:罚黑为14 300/46 656,状元为561/46 656,对堂为720/46 656,三红为2 500/46 656,四进为1 875/46 656,二举为9 300/46 656,一秀为17 400/46 656。本文研究博饼游戏的持续时间分布问题,在这个游戏中,持续时间与游戏中投掷骰子的次数成正比。经查阅文献,发现此问题与概率统计学中著名的“赌徒输光”[9-13]问题有相通之处。因此,本文应用马尔可夫链方法,通过计算机编程计算,获得了投掷次数为800以内的概率分布,发现该分布可以用对数正态分布进行拟合,并进一步给出了精确计算数学期望的方法,获得了数学期望的精确有理数表示。
1 符号说明
为叙述方便,引入以下符号:设A0,A1,A2,A3,A4,A5,A6分别表示随机事件“罚黑”、“状元”、“对堂”、“三红”、“四进”、“二举”、“一秀”,记pj=P(Aj),j=0,1,…,6。一局游戏刚开始时,各类奖品都未分发出去,随着游戏的进行,剩余奖品数越来越少,直至所有奖品分发完毕,游戏结束。定义状态向量(i1,i2,i3,i4,i5,i6),其分量i1,i2,i3,i4,i5,i6分 别表示状元、对堂、三红、四进、二举、一秀奖项的剩余奖品数,则状态空间T={(i1,i2,i3,i4,i5,i6)│0≤i1≤1,0≤i2≤2,0≤i3≤4,0≤i4≤8,0≤i5≤16,0≤i6≤32,i1,…,i6为整数}。易知,状态空间包含151 470(2×3×5×9×17×33)个状态点,游戏初始状态为(1,2,4,8,16,32),游戏结束状态为(0,0,0,0,0,0)。
由博饼游戏的规则可知,某个时刻的状态只依赖于前一个时刻的状态,从当前状态转移到其他状态或自身都有确定的概率。因此,奖品剩余状态向量构成一个典型的离散马尔可夫过程,即马尔可夫链。从一个状态经过一步转移可达到的状态称为该状态的一步可达状态。
2 投掷次数的概率分布
2.1 概率分布的计算算法
设随机变量Z表示一局游戏需要的投掷次数。一局游戏开始,所有奖品都未分发,所以有:
(1)
考虑k=0 的情形。显然,只有当奖品全分完时,才不需要投掷骰子,所以有:
(2)
再考虑k>0 的情形。在奖品剩余状态为(i1,i2,i3,i4,i5,i6)时,设想第1次的投掷结果必定为事件Ai(i=0,1,…,6)中的某一个发生,显然事件Ai(i=0,1,…,6)两两互不相交,它们构成样本空间的一个完备事件组,有全概率公式为:
(3)

(4)

(5)

(6)
类似地分析,有:
(7)
(8)
(9)
(10)
(11)
将式(4)和式(6)~式(11)代入式(3),得:
(12)
对任意正整数k,要计算式(1),只需以式(2)为初始条件,按式(12)进行迭代即可,具体算法可描述为算法1。
算法1 计算累计概率分布:P{Z≤k},k=0,1,2,…,K。
Input:转移概率p0,p1,p2,p3,p4,p5,p6,正整数K。
Output:P{Z≤k}=P(k),k=0,1,2,…,K。
预分配2个6维数组P1、P2和一个1维数组P;
初始化:P1(0,0,0,0,0,0)← 1,P1(i1,i2,i3,i4,i5,i6)← 0,其他;
P(0)←P1(1,2,4,8,16,32);
fork← 1,k<=K,k++do
for each(i1,i2,i3,i4,i5,i6)∈Tdo
P2(i1,i2,i3,i4,i5,i6)←p0P1(i1,i2,i3,i4,i5,i6)+p1P1(⎣i1-1」,i2,i3,i4,i5,i6)+
p2P1(i1,⎣i2-1」,i3,i4,i5,i6)+p3P1(i1,i2,⎣i3-1」,i4,i5,i6)+p4P1(i1,i2,i3,⎣i4-1」,i5,i6)+
p5P1(i1,i2,i3,i4,⎣i5-1」,i6)+p6P1(i1,i2,i3,i4,i5,⎣i6-1」);
end
P(k)←P2(1,2,4,8,16,32);
for each(i1,i2,i3,i4,i5,i6)∈Tdo
P1(i1,i2,i3,i4,i5,i6)←P2(i1,i2,i3,i4,i5,i6);
end
end
2.2 概率分布的计算结果
对给定的正整数K,按节2.1方法计算Z在 {0,1,2,…,K} 上的概率分布。由于状态空间中的元素数目多达151 470,需计算机编程计算。以下是K=800 的计算结果。
表2是Z的累计概率分布表。从表2中可以看出,投掷数不超过220的概率为0.522 067,而投掷数不超过640的概率高达0.999 031。由Z的累积概率分布,很容易计算Z取某个整数值的概率P{Z=k}=P{Z≤k}-P{Z≤k-1}。
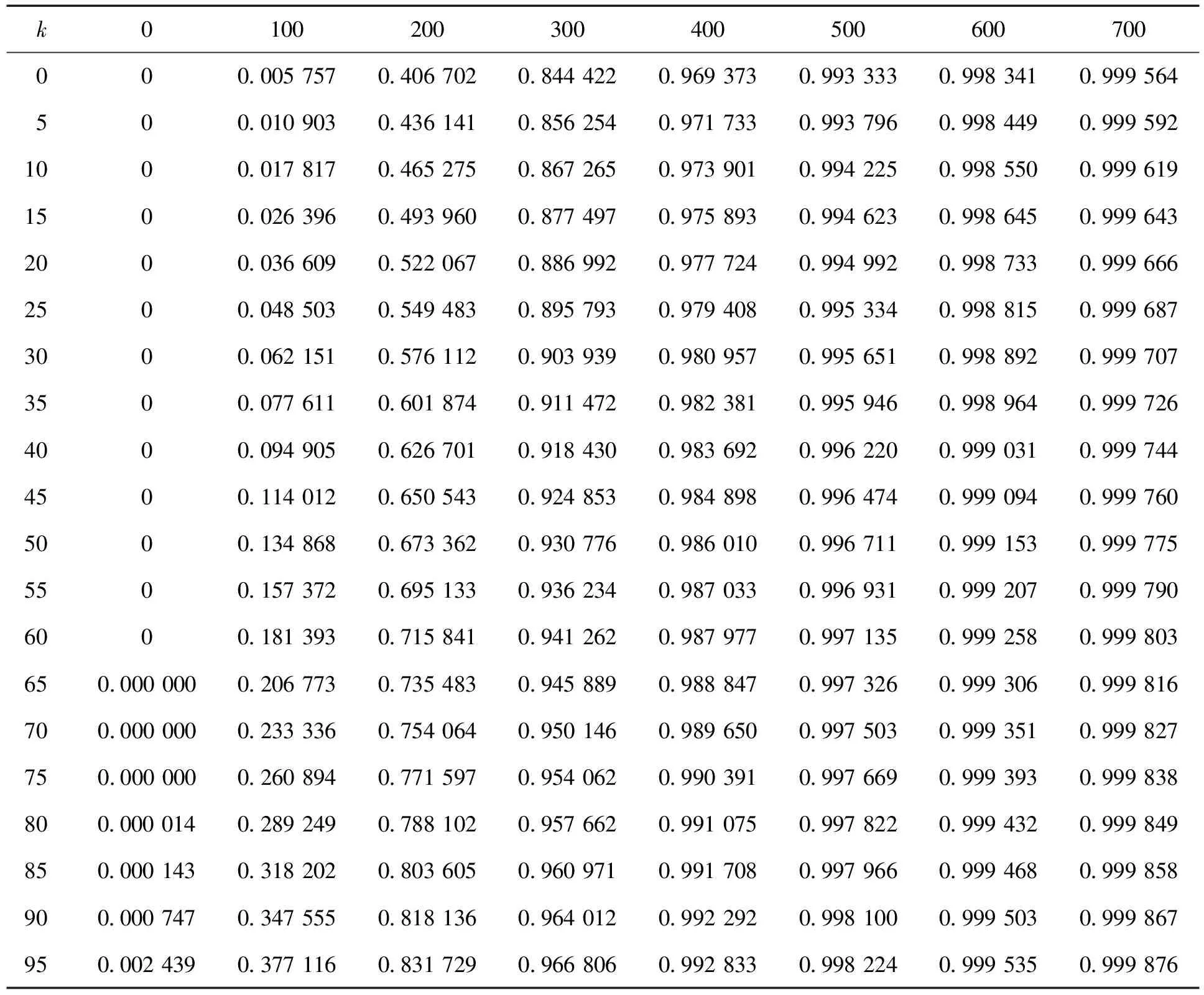
表2 投掷次数Z的累积概率分布表(P {Z≤k})
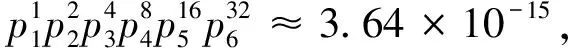
定义概率最大的投掷次数为最可能出现的投掷次数,则最可能出现的投掷次数为 196,其概率P{Z=196}=P{Z≤196}-P{Z≤195}=0.005 920 890,即1 000 局游戏中大约会出现6局是以196次投掷次数结束游戏的。
2.3 投掷次数Z的拟合分布
投掷次数Z的概率分布表虽已得出,但使用起来有些不便,能否使用已知的概率分布对其进行拟合呢?
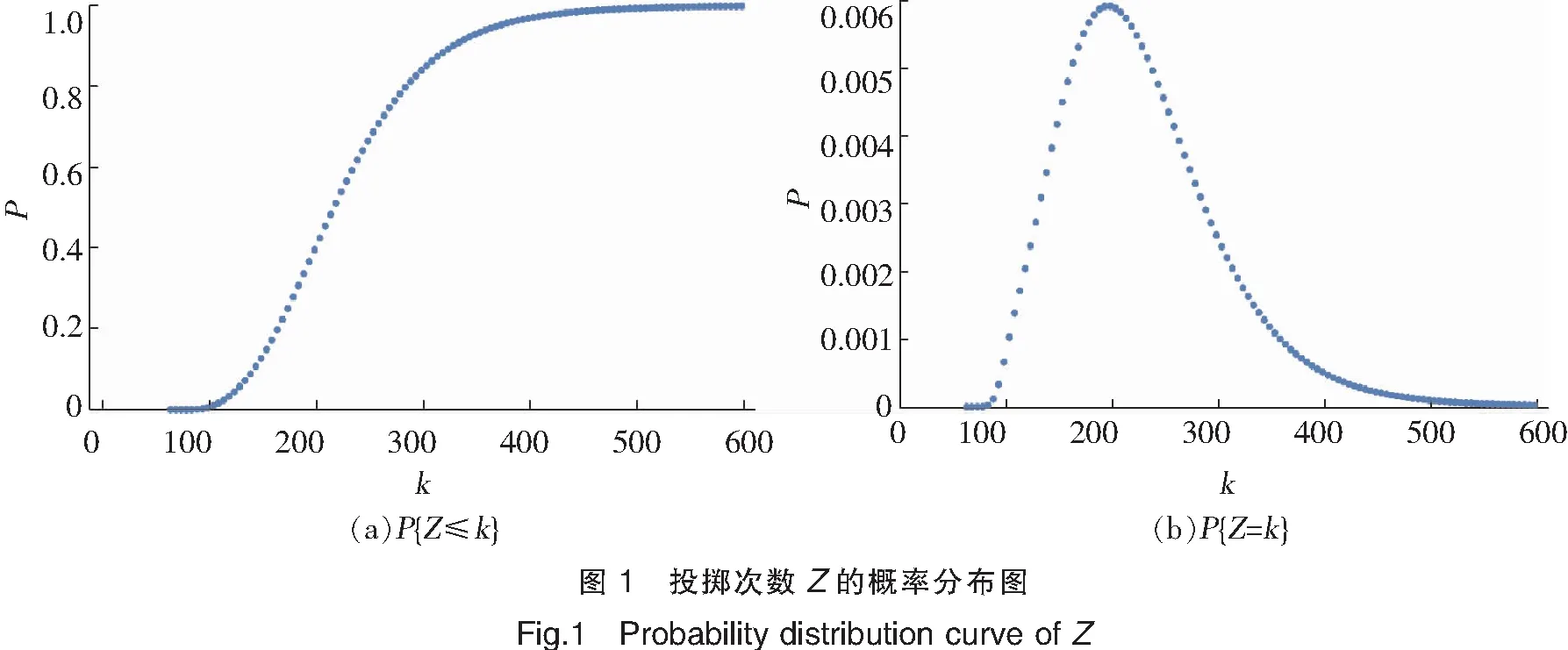
图1是投掷次数Z的概率分布图。由图1b可以看出,Z的分布是一种偏态分布,分别选择Γ-分布和对数正态分布对Z的概率分布用最小二乘法进行拟合,得出相应的参数。拟合效果见图 2,其中Γ-分布的形状参数α=9.289,尺度参数β=24.603,对数正态分布的参数μ=5.377 8,σ=0.328 4。从拟合效果来看,显然对数正态分布要优于Γ-分布。容易计算该对数正态分布的数学期望为 228.543,方差为 5 947.990,可作为Z的数学期望E(Z)和方差Var(Z)近似值,即平均要投 228.543次就可将奖品分配完毕。

3 投掷次数的数学期望
本节考虑E(Z)的精确计算问题。设奖品剩余状态为(i1,i2,i3,i4,i5,i6)时还需要的投掷次数的数学期望为E(i1,i2,i3,i4,i5,i6),类似节2.1的分析可得:
E(0,0,0,0,0,0)=0,
(13)

(14)
由式(14)可以解出E(i1,i2,i3,i4,i5,i6)。例如,当i1,i2,i3,i4,i5,i6全大于0时,有:
(15)
当(i1,i2,i3,i4,i5,i6)中出现0时,不失一般性,假设i1=i3=i5=0,i2,i4,i6>0,有:
(16)
由式(15)~式(16)可见,状态点(i1,i2,i3,i4,i5,i6)处的数学期望可以由一步可达状态点的数学期望递推算出,为此将状态空间T分层,对整数0≤k≤63,定义
Tk={(i1,i2,i3,i4,i5,i6)∈T|i1+i2+i3+i4+i5+i6=k}。
(17)
显然,T0={(0,0,0,0,0,0)},T63={(1,2,4,8,16,32)},Tk中的状态点的一步可达状态点一定在Tk-1中,计算E(Z)=E(1,2,4,8,16,32)的精确值的算法为算法2。
算法2 计算E(Z)=E(1,2,4,8,16,32)。
输入参数:p0,p1,p2,p3,p4,p5,p6;
初始化:E(0,0,0,0,0,0)← 0;
按式(17)构造Tk,k=0,1,…,63;
fork←1,k<=63,k++do
for each(i1,i2,i3,i4,i5,i6)∈Tkdo
由式(14)计算E(i1,i2,i3,i4,i5,i6)
end
end
输出:E(1,2,4,8,16,32)。
按算法2用数学软件Mathematica编程,计算得到E(Z)的精确值为:
E(Z)=(729 282 124 … 214 477 889)/(3 191 150 … 807 040 000)。
(18)
式(18)中分子为4 770位整数,分母为4 768位整数。由于篇幅所限,中间数位的数字略去。保留六位小数为:E(Z)=(729 282 124 … 214 477 889)/(3 191 150 … 807 040 000)≈ 228.532 698,与用对数正态分布计算的结果相比较,二者之间只差 0.01,再一次说明对数正态分布能很好地拟合投掷次数的概率分布。
