考虑颗粒破碎的堆石料大型三轴试验

吴鑫磊， 石北啸,*， 刘赛朝， 徐卫卫， 常伟坤

(1.河北工程大学水利水电学院， 邯郸 056004； 2.南京水利科学研究院岩土工程研究所， 南京 210029)

近年来，随着水电能源需求的不断扩大，在中国西部多条大江大河上，合理利用当地材料建造的堆石坝发展迅速，促使中国堆石坝的建设高度不断攀升至200 m级甚至300 m级(如糯扎渡、古水、如美等)。堆石料作为坝体主要建筑材料，可占据整体材料用量的90%以上，其强度及变形特性在很大程度上会影响堆石坝坝体整体的工作状态。而多数筑坝堆石料都是经过现场爆破开采出来的，其内部含有许多肉眼不可见的裂隙，且与砂卵石相比，堆石料浑圆度差，棱角居多，颗粒间常为点接触，在外力作用下极容易发生颗粒破碎现象[1]。颗粒破碎会引起堆石料级配特性的变化，进而引起堆石料整体物理力学特性的变化，颗粒破碎越严重，影响程度越大。因此，研究堆石料颗粒破碎规律，揭示颗粒破碎对堆石料力学特性的影响，对堆石坝的设计施工和安全生产以及对后期沉降的预测具有重大意义。

目前，中外学者对堆石料的颗粒破碎特性进行了大量研究，一部分学者致力于寻找影响堆石料颗粒破碎特性的因素。傅华等[2]通过室内堆石料的大型三轴和单轴试验，对堆石料的颗粒破碎特性进行了研究，证明母岩强度、级配、围压等都会对颗粒破碎造成影响；邹德高等[3]通过不同颗粒形状的堆石料进行三轴试验，认为在低围压状态下，颗粒形状对颗粒破碎的影响不可忽略；文献[4-5]通过对前人研究进行总结，认为应力路径、加载方式等也是影响堆石料颗粒破碎指标的重要因素，且就当前研究状态，定量评估各影响因素对颗粒破碎的影响程度存在一定难度；文献[6-8]则表示不论颗粒岩性、强度、大小、形状、级配及初始孔隙比等情况，最终的试验资料都会落在一个固定区域中。除此之外，也有一部分学者致力于量化颗粒破碎指标，尝试建立考虑堆石料颗粒破碎的本构模型，以此来描述及预测堆石料在外力荷载作用下的变形，如文献[9]通过对不同岩性、级配及干密度的堆石料进行大型三轴试验，建立了基于广义塑性理论基础之上考虑堆石料颗粒破碎的弹塑性本构模型；文献[10-11]基于堆石料的超大型三轴试验结果建立了缩尺效应与颗粒破碎之间的量化关系，认为可以此来外推及估算现场破碎现象；文献[12]建立了试验过程中反应堆石料颗粒破碎演化规律的数学模型。

在堆石料颗粒破碎特性研究方面，大多都是研究试验结束后堆石料的颗粒破碎情况与应力-应变曲线中峰值破坏点(以下简称峰值点)所对应的峰值强度、应变、剪胀性等之间的关系，关于峰值点处堆石料的颗粒破碎程度却无法得出。为准确反映峰值点处各特征参数与对应点处颗粒破碎之间的关系，使颗粒破碎与各力学参数之间关系的表达更为严密，基于此，现通过引入塑性功的概念，确定峰值点处颗粒破碎与强度、变形特性之间的关系，研究颗粒破碎对堆石料力学特性的影响，以期为堆石坝后期沉降的预测提供理论基础。

1 试验简介

试验用堆石料为料场爆破料，颗粒棱角明显，岩性为弱卸荷英安岩，堆石料的设计级配与缩尺后拟开展试验的级配曲线如图1所示。试验仪器采用的是南京水利科学研究院研制的大型三轴试验仪，试样尺寸为Ф300 mm× 700 mm，最大围压为4 MPa。

试验依据文献[13]进行，拟对试验级配的上包线、平均线和下包线，分别开展三轴饱和排水剪切试验，具体试验方案如表1所示。所用堆石料为自然风干，根据试验要求的干密度、试样尺寸和级配曲线，分60～40 mm、40～20 mm、20～10 mm、10～5 mm、5～0 mm 5个粒径范围称取试样，并采用振动击实法分层制样。制样完成后，采用水头饱和法(自下而上)对试样进行饱和。试样剪切过程中由计算机采集试样的轴向荷载、轴向变形、排水量或孔隙水压力，并同步绘制应力-应变曲线。为研究不同围压下试样的颗粒破碎特性，剪切过程中，应力-应变曲线无论是否出现峰值点，均剪切至轴向应变的15%。试验用料、试验设备及成样状态如图2所示。

图1 堆石料级配曲线Fig.1 The grading curve of rockfill material

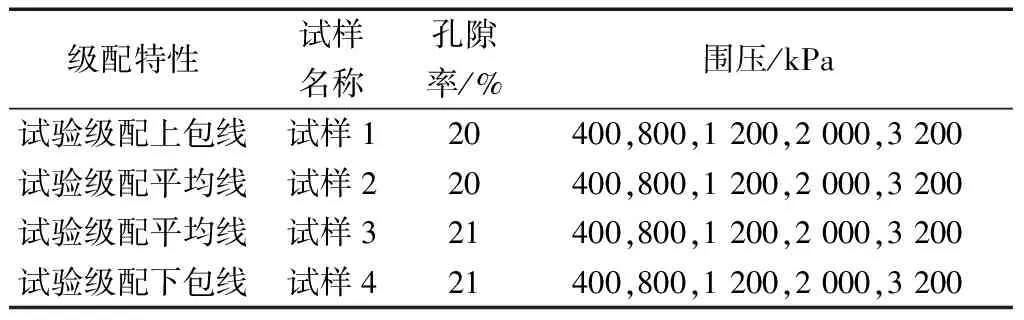
表1 试验方案Table 1 The testing programing

图2 试验用料及试验设备Fig.2 The test materials and test equipment

2 试验结果分析

2.1 颗粒破碎分析

对三轴剪切试验后的试样进行颗粒筛分，筛分后的各粒径含量增量如图3所示。

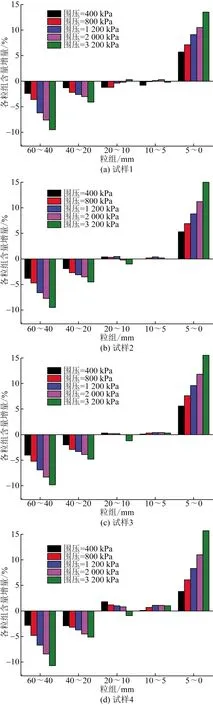
图3 试验后各粒组含量增量Fig.3 The content increment of different particle after test

由图3可知：试验后经过筛分的试样，其各粒组的粒径含量均有一定程度的变化，总体表现为20～60 mm的大颗粒含量明显下降，5 mm以下的细颗粒含量明显上升，而5～20 mm的中等颗粒含量则在原始粒径含量上下波动，并无明显差异。对不同级配的试样及相同试样的不同围压下颗粒破碎的增量进行分析，认为围压越大，大颗粒越容易受到挤压而发生颗粒破碎并填充到孔隙中，从而造成该粒径颗粒含量降低，导致5 mm以下的细颗粒含量增高。此外，从图3中可以看出，与试验后的其他试样相比，试样4中 5～20 mm的颗粒含量波动明显，分析认为试样4中的细粒含量较少，初始孔隙率较大，故对试样施加围压后，相较于试样1、2、3，该试样的颗粒更容易在围压作用下先行破碎，从而导致大颗粒破碎成大量中等颗粒及少量细颗粒；此时试样的中等颗粒填充到孔隙中，密实度提高，进而若再对其施加较大的围压，试样中颗粒破碎形态与其他试样则基本相当，但总体表现出该试样试验后的细颗粒含量增加最为明显。因此可以认为，初始孔隙率越大，级配越不良，试样剪切后的颗粒破碎现象越严重。

试样4在不同围压下试验后的颗粒级配曲线如图4所示。由图4可知，试验围压越大，产生的颗粒破碎越大，颗粒破碎导致细颗粒含量增加，试样级配曲线上移。

图4 试样4试验前后级配曲线变化Fig.4 Changes of grading curve of sample 4 before and after test

2.2 试样初始状态对颗粒破碎的影响

为了描述堆石料在试验前后各粒径含量的变化，定量分析堆石料颗粒破碎对其物理力学特性的影响，采用Marsal[14]提出的颗粒破碎率Bg来描述堆石料颗粒破碎的程度，具体计算公式为

Bg=∑|Wk|=∑|ΔWki-ΔWkf|

(1)

式(1)中：∑|Wk|为试验前后级配曲线上粒组变化量总和，%；ΔWki为试验前级配曲线上某级粒组的含量，%；ΔWkf为试验后级配曲线上相同粒组的含量，%。

堆石料三轴试验完成后颗粒破碎率Bg的试验结果如图5所示。从图5中可以看出，在低围压阶段，4组试验的颗粒破碎率基本相同，随着围压的增大，颗粒破碎率逐渐增大；且围压较小时颗粒破碎率增长较快，围压较大时，颗粒破碎率增长速度较慢，即颗粒破碎率增加的速率在逐渐减小。

外力作用导致堆石料颗粒破碎，是试样变形、体积变化的主要原因，体积变化势必引起试样的孔隙率改变，因此，试样孔隙率与其颗粒破碎间存在联系。图5中试样2和试样3的级配相同、初始孔隙率不同，从图5可以反映出，同一级配的堆石料，在相同围压下，试样的初始孔隙率越大，试验造成堆石料的颗粒破碎越大，这主要是因为试样内部存在的孔隙越大，细颗粒的填充效果就越差，在外力作用下带有棱角的颗粒更容易产生应力集中而发生颗粒破碎。需要注意的是，此处是试样的初始孔隙率，当试验开始后，试样内部颗粒发生移动或破碎，试样的孔隙率就会不断地发生变化。

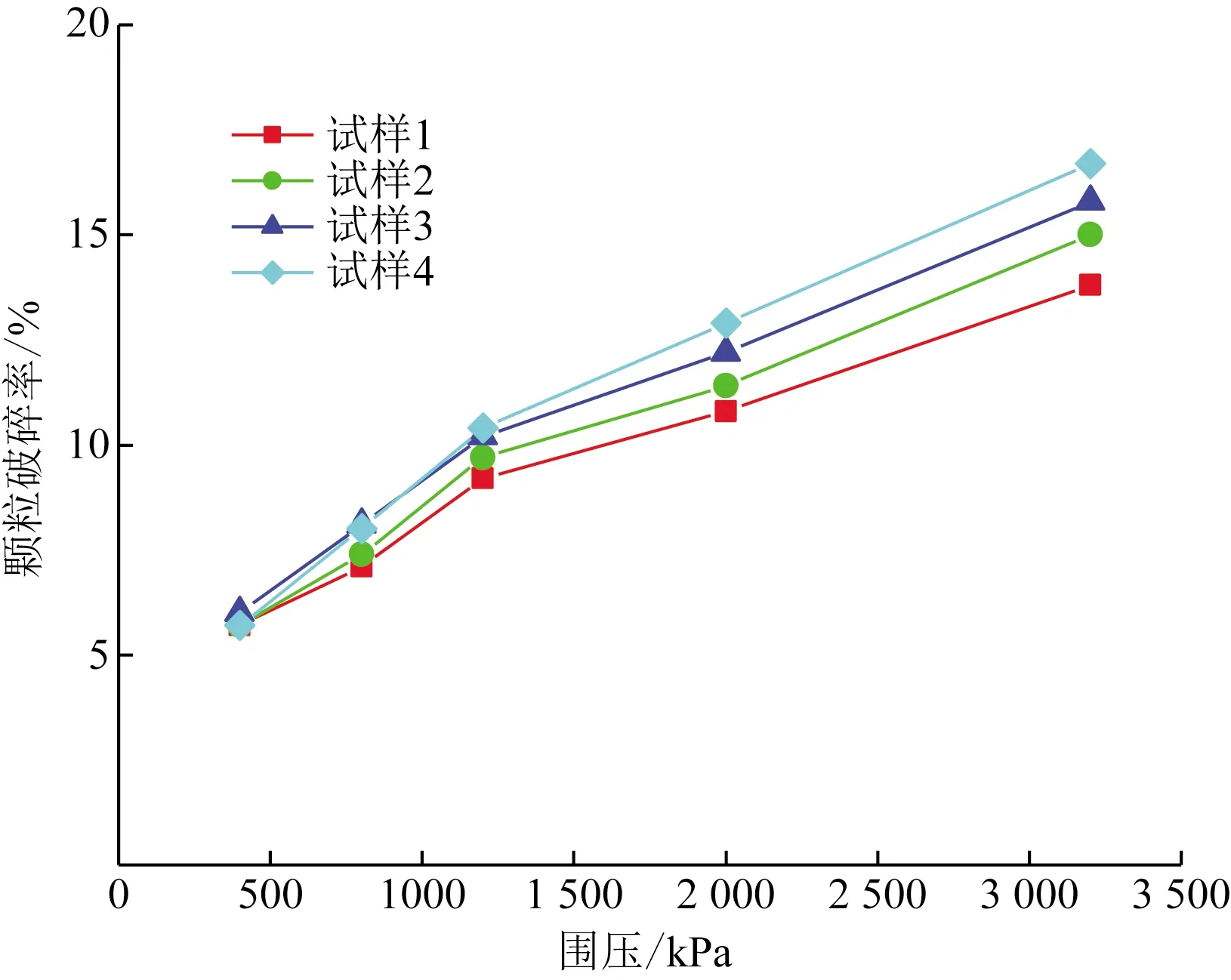
图5 颗粒破碎率与围压的关系Fig.5 Relationship between particle breakage rate and confining pressure

2.3 塑性功与颗粒破碎的关系

通过图5可知，试样的颗粒破碎与级配、围压及孔隙率存在某种联系，尹振宇等[15]也通过三轴试验证明即使试样达到峰值破坏点以后，颗粒破碎也会随轴向应变的增加而增加，即试样的级配、孔隙率、应力水平、试验停止时间等试验条件都会对颗粒破碎产生影响，故单一使用其中某一条件来表达试样的颗粒破碎程度存在缺陷。采用能量方程的相关理论分析堆石料颗粒破碎变化规律，认为总的输入能量(能耗量)包含了级配、孔隙率、试验时间等试验条件的影响，则可以将影响颗粒破碎的主要因素考虑进来，具体描述如下。

在试样剪切过程中的外力做功(总输入能量)W，其一部分转化为弹性功(弹性变形能)We，另一部分转化为塑性功(塑性变形能)Wp，即

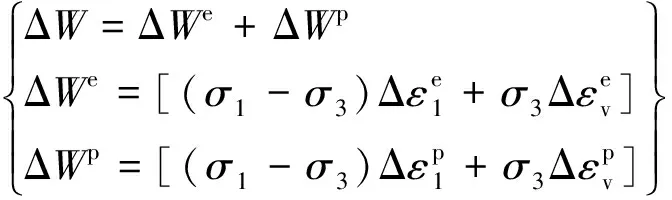
(2)

由于在堆石料的三轴剪切试验中堆石料的颗粒破碎属于不可逆行为，过程中如发生颗粒位移或颗粒破碎，可认为已经产生了不可逆的塑性变形，故在堆石料三轴剪切试验中总的能量变化可近似等于塑性功(塑性变形能量)Wp的变化，即

(3)

式(3)中的塑性功即为三轴剪切试验过程中正应力(σ1-σ3)与轴向应变ε1及围压σ3与体积应变εv曲线所围成的面积之和。

从图6可以看到，尽管试验条件不同，但试验的颗粒破碎率与塑性功之间存在良好的双曲线关系，计算公式为

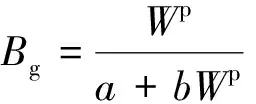
(4)

式(4)中：a、b为与堆石料颗粒自身性质有关的参数。从式(4)可以看出，随着外荷载做功的不断增大，堆石料颗粒破碎逐渐增大，但颗粒破碎增加的幅度在逐渐减小，可以认为在某一极大外荷载作用下，堆石料的所有颗粒均已破碎至无法继续破碎，其颗粒破碎率将逐渐趋近于定值。

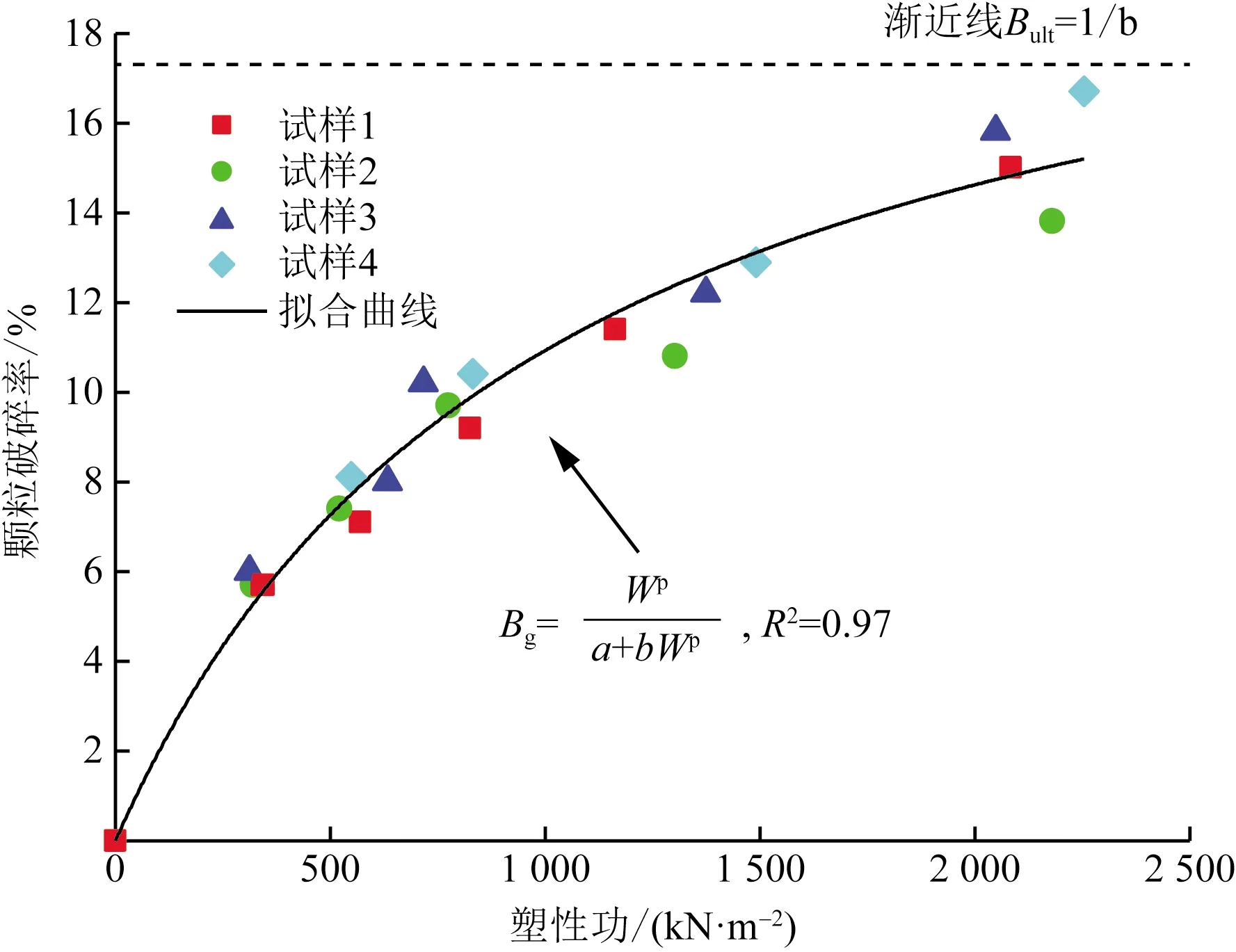
Bgult为堆石料颗粒破碎的最大程度图6 颗粒破碎率与塑性功的关系Fig.6 Relationship between particle breakage rate and plastic work

2.4 颗粒破碎对剪胀性、软化性及强度特性的影响

许多学者[6,10,16]研究表明，堆石料在应力作用下会发生颗粒破碎，使得其强度包线呈现向下弯曲的非线性特性，而堆石料的剪胀规律及软化特性则是建立堆石料数值模型的基础，因此，有必要分析颗粒破碎对堆石料剪胀、软化及强度特性的影响。

2.4.1 颗粒破碎对剪胀特性的影响

不同试样峰值点所对应的剪胀率与围压之间的关系曲线如图8所示。由图8可知，围压越小，剪胀越明显，剪胀率随试验围压的增大而逐渐减小并趋近于零。如前所述，随着试验围压的增大，试样在固结和剪切过程中发生颗粒破碎，堆石料的颗粒破碎导致了试样剪胀，颗粒间进行相对位置重新调整及细颗粒再填充，剪胀状态逐渐减弱；当剪切的轴向应变足够大时，试样内部颗粒排列及填充达到最佳状态，体积应变基本保持不变，逐渐进入剪胀率为零的临界状态。

图7 轴向应变-体积应变曲线Fig.7 The axial strain-volumetric strain curve

图8 峰值点处剪胀率与围压的关系Fig.8 Relationship between dilatancy rate at peak point and confining pressure

郭熙灵等[18]对峰值点处的剪胀率与颗粒破碎的关系也进行了研究，但在分析二者关系时，使用的是试验停止时的颗粒破碎率Bg，而不是峰值处的颗粒破碎率Bgf，事实上，轴向应变、加荷时间的长短等也会对堆石料的颗粒破碎特性造成影响，即在应力-应变曲线中出现强度峰值点后还会有颗粒破碎的发生。根据文献[19]的有关结论，此处用峰值点处塑性功的大小推求其对应点处的颗粒破碎率，进而研究峰值点处剪胀率df与对应点处颗粒破碎特性的关系，峰值处的塑性功由式(3)求取。

试验峰值点处剪胀率与颗粒破碎率如图9所示，由图9可见，随着峰值点处颗粒破碎率增加Bgf，堆石料峰值点处的剪胀特性逐渐减小。另外还发现，峰值点处的剪胀率与颗粒破碎率在倒数轴坐标中近似呈现线性关系，计算公式为

df=(dεv/dε1)f=c+d(1/Bgf)

(5)

式(5)中：c、d为与堆石料颗粒自身性质有关的参数。当堆石料没有发生颗粒破碎时，式(5)表示颗粒在应力作用下进行重新排列引起的体积变形。

2.4.2 颗粒破碎对软化特性的影响

4种试样在围压为1 200 kPa时的应力应变关系曲线如图10所示。由图10可知，除试样4外，其他试样都表现出轻微软化特性。这主要是由于试样1、2、3的级配良好，细颗粒含量较多，且孔隙率较小，颗粒排列紧密，故发生颗粒破碎的几率较小，更多的是内部颗粒间的位置错动与滚动翻越。对于试样4，其细颗粒含量较少，孔隙率较大，外力作用更多的是使结构发生颗粒破碎，颗粒破碎导致内部颗粒间填充较好，试样变得紧密，故呈现出硬化特性。

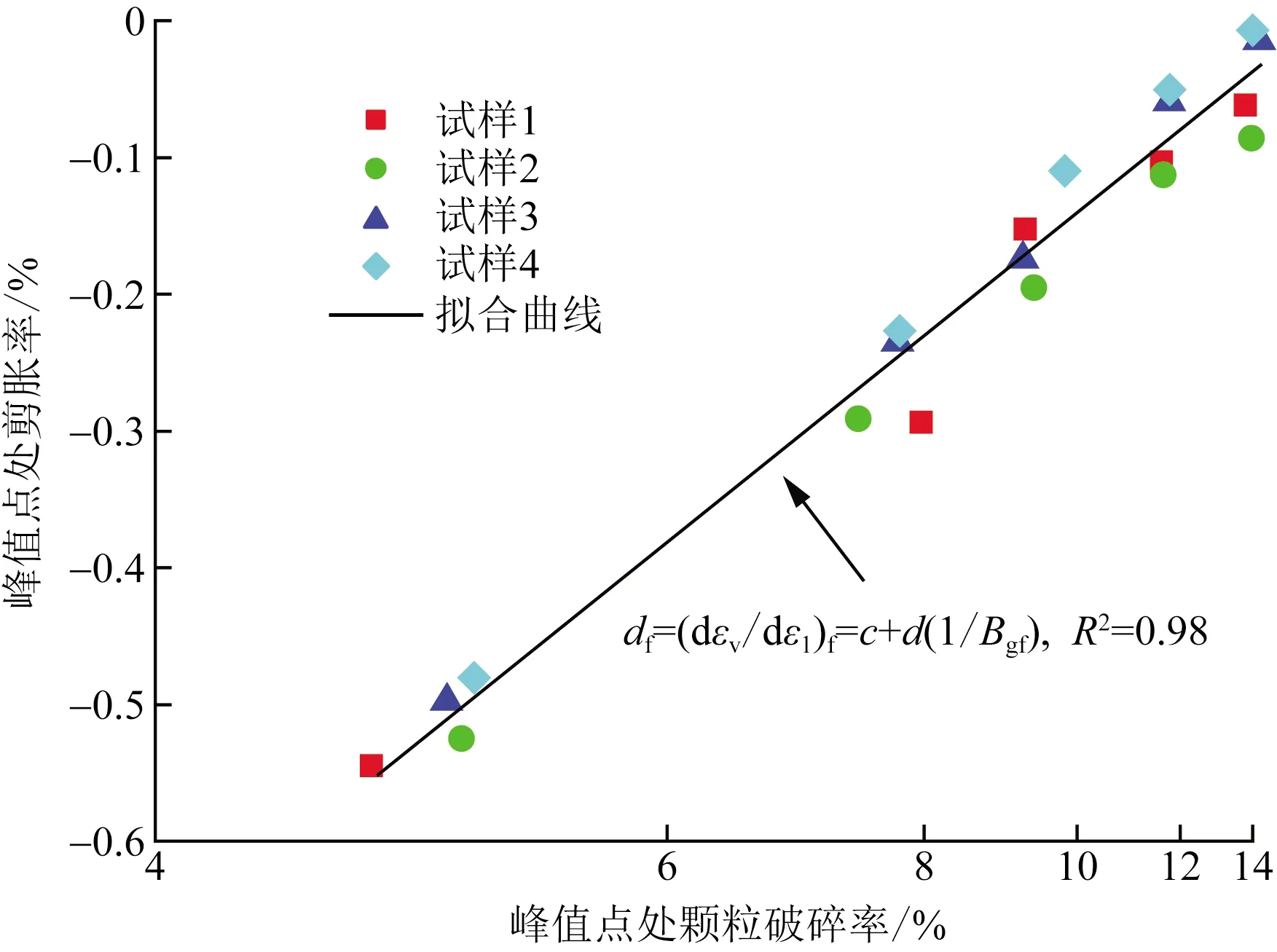
图9 峰值点处剪胀率与颗粒破碎率的关系Fig.9 Relationship between dilatancy rate and particle breakage rate at peak point

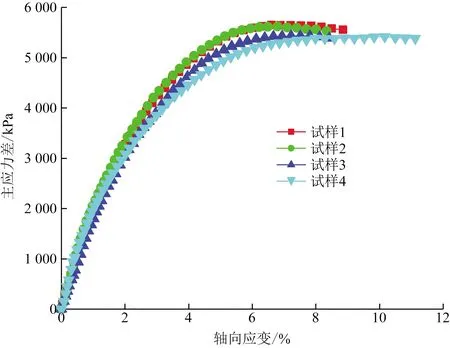
图10 σ3=1 200 kPa时的应力-应变曲线Fig.10 Stress-strain curve at σ3=1 200 kPa

2.4.3 颗粒破碎对强度特性的影响

各试样峰值内摩擦角与颗粒破碎率的关系曲线如图11所示，可知随着颗粒破碎率的增加，堆石料的峰值内摩擦角在减小，即堆石料的颗粒破碎会导致其抗剪强度的降低，但降低的速率在逐渐减小。对比试样1与试样4关系曲线可以发现，在颗粒破碎的初期前者的抗剪强度大于后者，随着颗粒破碎的增加，后者的抗剪强度高于前者，产生这种情况的原因主要是由于试样1的粒径小于5 mm的细颗粒含量高于试样4，在相同颗粒破碎的情况下，试样1内部更密实，抗剪强度更高；而随着颗粒破碎的增加，试样1中起骨架作用的粗颗粒越来越少，细颗粒相互排列但颗粒间的孔隙无法用更小的颗粒进行填充，其密实度远不如试样4，故在较高的颗粒破碎率的情况下，试样4的抗剪强度较高于试样1。

峰值内摩擦角与峰值点处颗粒破碎率的关系曲线如图12所示。从图12中可知，4组试样在峰值破坏点处的内摩擦角与颗粒破碎率间存在较为良好的线性关系，计算公式为

图11 峰值内摩擦角与颗粒破碎率的关系Fig.11 Relationship between internal friction angle at peak point and particle breakage rate

图12 峰值点处内摩擦角与颗粒破碎率的关系Fig.12 Relationship between internal friction angle and particle breakage rate at peak point

φf=e+fBgf

(6)

式(6)中：e、f为与堆石料颗粒自身性质有关的参数。当堆石料没有发生颗粒破碎时，式(6)中参数e表示颗粒在应力作用下进行重新排列产生的最大内摩擦角。

对于应用于黏土的剑桥模型来说，剪胀率与应力比之间存在一一对应的线性关系，也有一些学者[19]对砂土峰值点处的剪胀率df与峰值点处的主应力比(σ1/σ3)f之间的关系进行研究也证明二者之间线性相关。不同级配及孔隙率的堆石料峰值点处的剪胀率与其所对应的主应力比之间的关系如图13所示，可以发现试验得到的数据在图中近似呈线性关系，所得拟合结果为

df=(dεv/dε1)f=g-h(σ1/σ3)f

(7)

式(7)中：g、h为与堆石料颗粒自身性质有关的参数。当峰值点处的应力比(σ1/σ3)f=3.62时，所对应的剪胀率df=0，此时试样处于体变由剪缩向剪胀过渡的转折点。

图13 峰值点处剪胀率与主应力比的关系Fig.13 Relationship between dilatamcy ratio and principle stress ratio at peak point

3 结论

通过堆石料高应力状态下的室内大型三轴试验，分析堆石料在不同孔隙率、级配及应力状态下的颗粒破碎情况，并对峰值点处颗粒破碎与其剪胀性及强度特性的影响进行分析，得到以下结论。

(1)三轴试验的颗粒破碎导致堆石料级配发生变化，试验后20～60 mm的大颗粒含量减少，小于5 mm的细颗粒含量增加，5～20 mm的中等颗粒含量上下波动，变化不大，且试样的孔隙率越大，级配越不良，颗粒破碎现象越严重。

(2)堆石料颗粒破碎率与塑性功之间存在良好的双曲线关系，颗粒破碎随外荷载做功而不断增大，但增幅会逐渐减小。

(3)堆石料峰值点处剪胀率与颗粒破碎率在倒数轴坐标系中呈线性相关，与对应的主应力比近似呈线性相关；峰值点处颗粒破碎率与峰值内摩擦角呈线性相关，随着峰值点处颗粒破碎率的增大，其峰值内摩擦角的值在逐渐减小。

以上结果针对的是某一级配范围内同种堆石料的试验结果，对于其他母岩性质及级配的堆石料，其结果有待进一步研究。