基坑降水引起地表沉降计算系数Ms的修正
2022-02-18于澜涛徐光黎
于澜涛, 徐光黎
(中国地质大学(武汉)工程学院, 武汉 430000)
随着城市建设规模的不断扩大,地下空间的开发产生了许多基坑,这些基坑的开挖,使原有基坑周围的水、土应力平衡受到破坏,危及地下管线、道路、地面建筑物的安全。理论研究的滞后一方面导致了基坑承压水降水过于经验化、保守化;另一方面,也可能在特殊情况下造成基坑降水事故。武汉地区工程地质、水文地质条件复杂,对于基坑降水所引起周围环境的地面沉降,没有形成较为适用、准确的计算方法,目前主要采用的是《湖北省地方标准基坑工程技术规程DB42/159—2004》[1]中的沉降计算方法,但经验系数Ms的取值依据不足,具有很强的随机性、不确定性,更无法判断其合理性,在这种情况下,预测的沉降量往往是不令人满意的。因此需要对基坑降水引起周围环境某点的地面沉降计算方法进行优化,推动武汉市基坑工程的发展与进步。
李玉选等[2]根据有效应力原理将沉降分为由减压降水及疏干降水引起的两部分优化分层总和法。姚文龙等[3]结合渗流力和重度等因素,对基坑周边土层进行划分,并提出以随机介质理论计算沉降量的方法,土体重度变化在地面沉降中起主导作用,渗流力的作用只占到30%。李瑛等[4]提出了坑外水头降深与降水量的公式,结合渗透系数、地连墙长度等因素优化了沉降计算公式。江杰等[5]考虑渗流力和止水帷幕等因素,提出了简便的沉降计算公式,将误差控制在12%以下。谷栓成等[6]应用不同含水率下的土体重度计算地表沉降量,结合随机介质理论预测结果,与现场实测值比较误差小于10%;李又云等[7]采用ABAQUS软件建立三维流固耦合模型,根据不同工况开挖结果证明开挖引起的地表沉降小于降水引起的地表沉降。李志平[8]结合土体水理性质之间的关系提出修正系数。李文广等[9]以Merchant流变模型模拟降水引起含水层变形的时间效应,随机介质理论模拟地面沉降空间分布规律,导出一种计算沉降的方法。张陈蓉等[10]采用位移控制有限元法(displacement controlled finite element method,DCFEM)和位移控制两阶段简化理论方法,分析得到基坑变形和土体沉降的方法。王建秀等[11]按照逆回弹-变形协调原理,采用顶板逆回弹参数优化分层总和法,准确计算单点沉降及地面沉降值。
目前对于基坑降水导致土层分层沉降规律的研究较少,因此,现从土层分层沉降特点的角度分析,在降水后,根据土层分层监测数据得出了土体分层沉降规律,确定基坑周边土体发生沉降的主要压缩层,仅计算主要压缩层沉降量并与实际沉降量比较,修正经验系数,以某工程实例,验证修正系数的准确性。
1 计算方法
目前《湖北省地方标准基坑工程技术规程(DB42/159—2004)》[1]中降水引起地面沉降计算公式为
(1)
Δσ′i=γwΔH
(2)
式中:S为降水引起的沉降量,m;规范中经验系数Ms=M1M2,其中M1由土层性质决定,对于一般黏性土M1可取0.3~0.5;粉质黏土、粉土、粉砂互层M1可取0.5~0.7;淤泥、淤泥质土M1可取0.7~0.9。M2由降水时间决定,当降水时间小于3个月时M2可取0.5~0.7;当降水时间大于3个月时M2可取0.7~0.9;Δσ′i为第i层土的有效应力增量,kPa;γw为水的重度,kN/m3,取值10 kN/m3;ΔH为土层降水前后的水位降,m;hi为第i层土层厚度,m;Ei为第i层的压缩模量,kPa。
从式(1)中可以看出:沉降量S的计算是由覆盖层、过渡层及承压含水层共同决定的,实际工程中,当抽取地下水时,相对隔水层以上的地层中地下水位变化甚微,将其全部纳入计算存在一定不合理性。现结合武汉地区凯德广场深基坑分层沉降规律,分析降水后各土层压缩情况,找出主要压缩层,进而计算地面某点的沉降量并修正经验系数。
2 算例分析
2.1 工程概况
凯德广场古田深基坑地面标高为+24.000 m,相对标高-1.500 m;基坑开挖面积约为6.5×104m2,周长为1 005.0 m,基坑开挖深度为14.40~15.80 m。该基坑采用顺作法的总体设计方案,采用不落底式止水帷幕+分区降水+坑内设置疏干井和减压井处理下部承压水。承压水主要赋存于②-4交互层及③-1粉细砂层中;根据抽水试验测得其静止承压水位在6.95 m,相当于标高17.35 m左右。
2.2 工程地质模型
结合钻孔资料,基坑开挖及降水深度以内土体共划分6层,各土层分布如图1和表1所示。

图1 工程地质剖面图Fig.1 Engineering geology profile
2.3 沉降计算分析
为确保施工期间的结构及建筑物的稳定和安全,凯德广场古田深基坑项目对周围环境以及支护工程进行了较为详细地监测,包括对周围道路、管线、坑外水位等。监测局部平面图如图2所示。监测自2014年12月16日至2015年12月21日,共331期,其中R01~R67为道路位移监测,JS01~JS36为给水管线位移监测,SW01~SW12为坑外地下水位监测。

表1 各土层分层情况表Table 1 Stratification of each soil layer

图2 监测平面示意图(局部)Fig.2 Monitoring plan(local)
凯德广场古田项目深基坑工程地下设整体3层地下室,基坑开挖深度为14.40~15.80 m,挖穿隔水层,基坑坑底大部分位于(②-4)粉砂夹粉质黏土夹粉土的交互层上。已知条件有:D为含水层厚度,解析法中将各层含水层合并视作一层,D=52.8 m;h为承压水水位降深值,保持水位低于坑底1 m,案例中目标降深h=9.88 m;k为含水层综合渗透系数,k=14.23 m/d;r0为基坑等效圆半径,基坑近似看作方形,边长a=251.3m,r0=0.59a=148.2m;R为影响半径,由抽水试验得R引=240 m,R=R引+r0=388.2m。
根据《湖北省地方标准基坑工程技术规程(DB42/159—2004)》[1]中承压完整井稳定流计算方法,土层物理力学参数如表1所示。地面某点水位降幅h为

(3)
式(3)中:Q为总抽水量;r为各点距基坑的距离。
对凯德广场深基坑周边道路以及管线沉降进行计算,选取降水10个月后的平稳阶段沉降值进行对比。结果如表2所示。其中M2宜取0.9,M1经比对分析皆取规范中提供的参数区间下限值,即各层土经验系数Ms:黏土0.27、黏土夹粉砂0.45、黏土夹粉土0.54、粉土夹黏土、粉砂0.63、粉细砂0。误差Δ=(S规-S实)/S实。
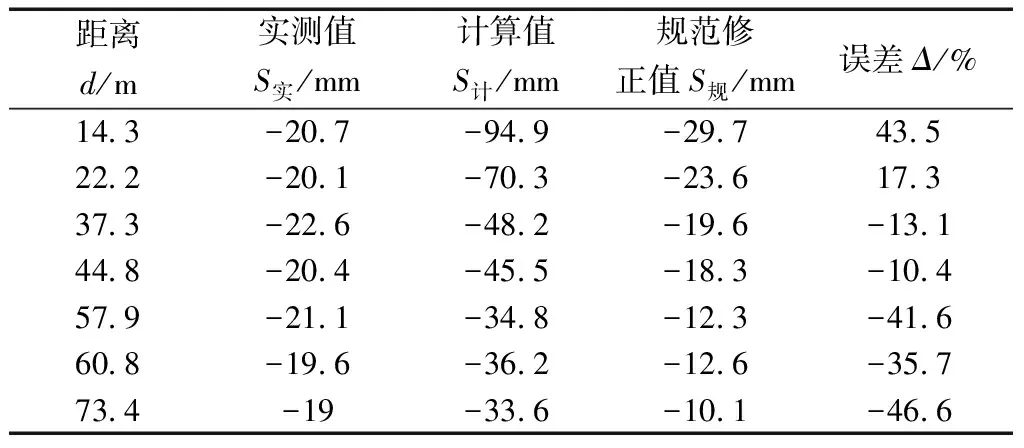
表2 沉降计算值与实测值对比Table 2 Comparison of calculated settlement value and measured value
根据计算结果(图3),运用规范中的公式计算的沉降量比实际监测值偏大,根据规范中推荐经验系数人为修正后,平均相差1~2倍。并且经验系数的选取具有很强的随机性、主观性,无法做到在实际工程中精确判断。
2.4 分层沉降规律研究
为有效分析土层分层沉降规律,选取基坑周围8个沉降点(FC01~FC08)分别布置沉降环,进行分层沉降监测,监测点平面分布图如图4所示。
选取具有代表性的监测点FC05,再确定控制不同土层的沉降环,分别为①杂填土、②-1(2)黏土夹粉砂、②-3黏土夹粉土、②-4互层土(粉土夹黏土、粉砂)、③-1粉细砂。图5为FC05点分层沉降随时间和地下水位变化情况。

图3 沉降计算值与实测值对比曲线Fig.3 Comparison between calculated and measured values of road settlement

图4 分层沉降监测点平面示意图Fig.4 Layout of stratified settlement monitoring points
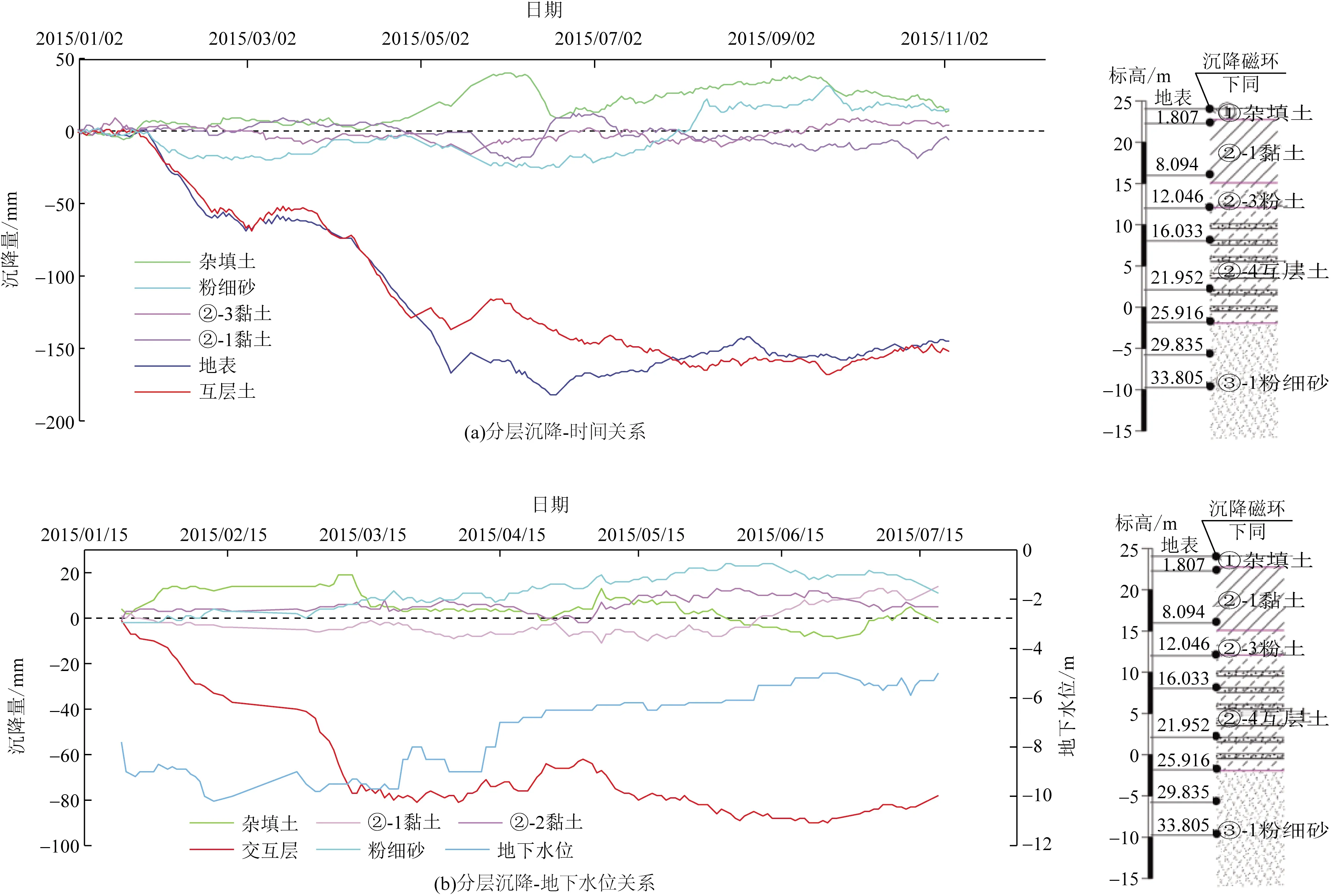
图5 FC05土层分层沉降与时间和地下水位关系曲线Fig.5 Relationship curve between stratified subsidence and time, groundwater level of FC05 soil layer
通过对分层沉降随时间变化数据可知,交互层压缩量最大,粉细砂层次之,其中杂填土、黏土层主要发生膨胀而并非压缩。可见在基坑降水开挖初期,各土层的沉降量是微乎其微的,变化范围在0~10 mm,持续时间为20~30 d;随着基坑降水时间增加,交互层压缩量迅速增加,变化速率达3~4 mm/d,且变化趋势与地面沉降几乎一致;待基坑降水工作完成,交互层的沉降逐渐趋于稳定,上覆土层发生膨胀,下伏粉细砂层的固结,是该阶段造成地表沉降变化的主要原因。
综上,凯德广场古田项目地面沉降、分层沉降的监测数据表明,各土层沉降受影响程度关系为:交互层>粉砂层>黏土>杂填土。得出的结论如下。
(1)交互层是地面沉降的主要压缩层,约占90%。
(2)黏土、杂填土层由于受②-3粉土层的阻隔,以及基坑降水主要在交互层和细砂层中的承压水,水头降深尚未波及,即黏土层没有发生越流,故黏土层、杂填土层为非压缩层。
(3)粉砂层的沉降量与水位(水头)变化密切相关,基本是同步的,可不考虑滞后效应,由图5(b)可知,粉砂层随水头下降而压缩,随水头上升而回弹亦为非压缩层。
3 经验系数Ms值优化修正
3.1 系数Ms的修正
基于《湖北省地方标准基坑工程技术规程DB42/159—2004》[1]中提供的经验系数Ms选取方法,分析经验系数的取值的影响因素,结合凯德广场深基坑分层沉降规律对经验系数Ms的选取进行优化。
3.1.1 经验系数Ms的影响因素
通过对凯德广场古田深基坑项目监测数据分析,进一步细化分析影响修正系数的主要因素,包括降水时间t、地下水位(水位降深h)、距离d、土层压缩模量E,以下为不同因素的影响。
(1)水位降深h。基坑降水是造成沉降的首要因素,根据计算结果显示,水位降深愈大,沉降愈大,若地下水位在主要压缩层波动时,对整体沉降影响更加显著。
(2)降水时间t。基坑周边环境沉降随时间推移发生连续性变化,①降水初期,由于土层沉降的滞后效应变化缓慢;②随着基坑降水量增加,沉降以一定速率增加;③降水工作完成后一段时间,沉降趋于稳定值。
(3)土层性质。主要考虑土体的压缩模量E。
3.1.2 经验系数Ms值修正
结合凯德广场分层沉降规律,仅计算交互层(黏土夹粉砂、粉土)的沉降量,各土层经验系数Ms取值黏土0、黏土夹粉砂0.45、黏土夹粉土0.45、粉土夹黏土、粉砂0.4、粉细砂0。计算结果如表3和图6所示。由计算结果可知,误差Δ=0~25%[Δ=(S修-S实)/S实],较原方法计算误差减少了50%,如图7所示。


表3 沉降修正值与实测值对比Table 3 Comparison of settlement modified value and measured value

图6 沉降修正值与实测值对比曲线Fig.6 Comparison of road settlement repair value and measured value

图7 误差对比图Fig.7 Error comparison diagram
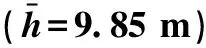
表4 M1与压缩模量E的关系Table 4 Relationship between M1and
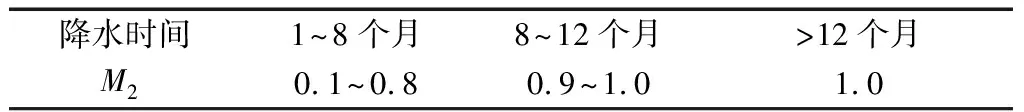
表5 M2与降水时间t关系Table 5 Relation between M2 and precipitation time
3.2 案例验证
为验证经验系数的修正结果,对香港中心深基坑沉降数据进行验证分析,如表6和图8所示,可见修正值S修较规范修正值S规,更加接近实际值,修正结果更贴合实际。
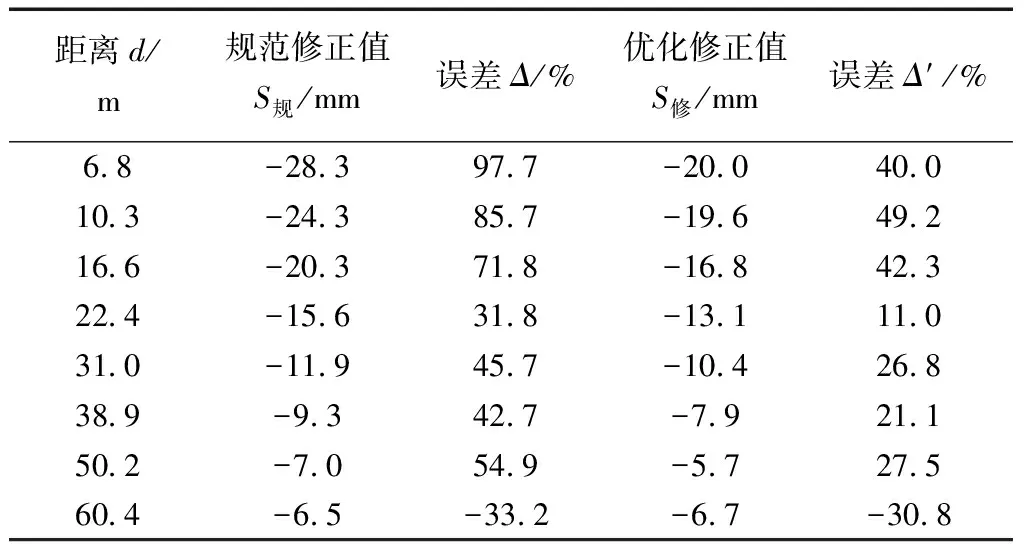
表6 沉降修正值与实测值对比Table 6 Comparison of settlement modified value and measured value

图8 沉降修正值与计算值对比曲线Fig.8 Contrastive curve of settlement modified values and calculated values
4 结论
(1)凯德广场深基坑从地层结构分析,杂填土层、粉砂层是非压缩层。杂填土土层中不存在水头下降;粉砂层随水头下降而压缩,随水头上升而回弹,所以计算中可不考虑其压缩量,主要压缩层为黏土层、交互层。
(2)综合对基坑周边沉降计算结果,分析经验系数Ms的影响因素,以凯德广场古田项目数据为依托,对规范中推荐经验系数选取方法进行修正。其中M1考虑与土层压缩模量E有关,区间为0.4~0.5(压缩模量E为8.0~3.1 MPa)。
(3)根据香港中心基坑沉降计算结果对比结果,误差Δ经修正减小了18.9%~57.6%,计算结果在工程可以接受范围内,修正系数更加符合实际情况,切实可行。
