临河基坑有限成层土体主动土压力计算
2022-02-18蔡忠伟朱彦鹏武开通马响响丁亚飞
蔡忠伟, 朱彦鹏, 武开通, 马响响, 丁亚飞
(1.甘肃省第六建设集团股份有限公司, 兰州 730000; 2.兰州理工大学土木工程学院, 兰州 730050; 3.甘肃省建设投资(控股)集团有限公司, 兰州 730050)
随着城市可利用土地逐年减少以及城镇居民对人文景观需求的激增,越来越多的建筑物开始临河、临湖修建。由于环境的特殊性加之地层的复杂性,基坑开挖过程遭遇了诸多难题。这些问题大都与土压力大小未知、土压力分布规律不明有关,尤其是临河条件下的挡土墙受力情况,进一步决定着挡土结构能否有效发挥作用。
对于有限土体土压力的计算,项龙江等[1]基于有限土体土压力计算理论,通过考虑尺寸效应,推导了小尺寸基坑土压力解析解,结果显示,小尺寸深基坑的土压力受尺寸效应影响明显。Greco[2]利用极限平衡方法对围护结构与岩石之间的有限土体进行理论分析,得出了相应的土压力表达式。王闫超等[3]采用薄层单元法推导了临近地下室外墙的挡土墙后主动土压力解析解,并与朗肯土压力公式等进行了比较,结果表明,墙土内摩擦角和黏聚力对主动土压力值影响明显。芮瑞等[4]研究了地下开挖引起地层损失对邻近地下挡土结构土压力和地表沉降的影响,结果表明:地层损失会使邻近基坑挡墙上部土压力增加,下部土压力减小。宁源等[5]建立了有限黏性土体模型,通过平衡方程推导出土体主动土压力系数表达式。朱彦鹏等[6]依托于库伦理论平面滑裂面假设以及极限平衡理论,扩大了主动土压力计算公式的应用范围,同时也指出为了提高经济效益,应当注意外摩擦角、黏着力的影响。徐日庆等[7]以有限黏性土为研究对象,基于塑性上限理论,得出了考虑土拱效应作用的主动土压力计算表达式,最后将解析解与模型试验所得数据对比发现两者比较接近,由此说明所得公式的正确性。此外,也有部分学者通过具体试验或者模拟的方法进行有限土体土压力的研究。Khosravi等[8]引入粒子图像测速法对土体平动模型进行分析,从而使得围护结构周围土体变形更加形象生动,更有利于验证研究的合理性。杨思敏[9]以静水条件下墙后有限无黏性土为研究对象,通过模型试验和数值分析的方法进行主动土压力研究,由此得出了土体的具体破坏形式和土压力分布规律。杨明辉等[10]针对无黏性土体,开展了墙后有限土体土压力试验,从而提出了土体的具体破坏形式及土压力分布规律。上述研究或通过理论分析或通过模型试验或通过数值模拟进行土压力研究,但都没有将临河条件考虑在内。李飞等[11]基于极限平衡法,通过考虑临河基坑与河流之间的有限土体,得出了不同破裂角情况下的主动土压力计算表达式,结合具体案例,发现所得公式符合实际要求,通过数值模拟发现,当基坑宽度与基坑深度之间的比值介于0.6~0.86时,将出现数值超过朗肯土压力的情况。孙俊[12]结合理论推导、室内模型试验、有限元数值模拟、现场监测等方法,以临河有限土体为研究对象,综合考虑多种因素对支护结构土压力的影响,最终为解决临河基坑难题指明了方向。
以上所述研究虽然考虑了临河条件,但并未考虑嵌固深度等因素的影响,致使计算结果跟实际情况有较大偏差。因此,在上述研究成果的基础上,现以临河的开挖基坑与河流之间的有限土体为研究对象,通过研究有限土体滑裂面的不同情况,来探讨临河基坑有限成层土体主动土压力的大小。
1 计算模型及参数说明
成层土体又称多层土体,是指地下土体并非一种土层,而是由多种土层组合而成。一般情况下,土层不仅包括黏性土层,还包括非黏性土层。为了研究方便,仅考虑多种黏性土层组合的情况。在计算时,以两层黏性土为例。由于研究对象为黏性土,所以不考虑渗流及水动力的影响,将河流以及地下水的作用看作静水压力,进行水土合算,计算模型如图1所示。
假定各层土的分界面与土体表面平行,在分析上层土的受力时,考虑到两层土体之间没有相对位移,所以不考虑下层土体的作用,通过对上层土体建立平衡方程,求解出上层土的主动土压力合力Ea1。计算下层土时,将上层土的重力考虑在内,通过对下层土建立平衡方程,求解出下层土的主动土压力合力Ea2。最终的土体主动土压力合力Ea由Ea1与Ea2叠加而成。

图1 有限土体示意图Fig.1 Schematic diagram of limited soil
2 计算假定
计算假定如下:①有限宽度土体为两层黏性土,各层土体均匀分布且各个方向性质相同;②考虑河岸的影响,即认为河岸与竖直方向的夹角为ψ;③挡墙为刚性体,忽略其变形;④挡墙背面竖直、粗糙,起挡土、止水作用;⑤河流足够宽,且不考虑河面的上下波动;⑥滑裂面为一平面;⑦填土表面水平;⑧上层土体与下层土体之间的交界面位于河面之上。
3 受力分析及方程的建立
有限土体达到临界状态的土压力即所求主动土压力,按照破坏情况的不同,分为以下两种情形。
3.1 情形一:在基坑底部滑裂
1)滑裂土体为楔形体且破坏面被河流所截
该情形是由于上层有限土体土层不稳定以及河流对河岸冲击太大造成的,裂缝从河岸坡面生成,然后沿着基坑底部方向不断延伸,最终形成贯通的滑移面,具体受力情况如图2所示,其适用条件为

(1)
式(1)中:H为基坑开挖深度;h为河面到地面的垂直距离;h0为河流深度;b为有限土体宽度;ψ为河岸与竖直方向的夹角;θ为滑裂面与水平方向的夹角;h+h0为地面到河底的距离;F为河流对河岸的作用力。
由B点出发向下作AB的垂线交CD于M点,由C点出发水平作BM的垂线交BM于P点。
设CP=T,则由S△BCM=S△BCP+S△CPM可知:
则有

(2)
滑动土体每延米重力:

(3)
式(3)中:γ1为上层土的容重。
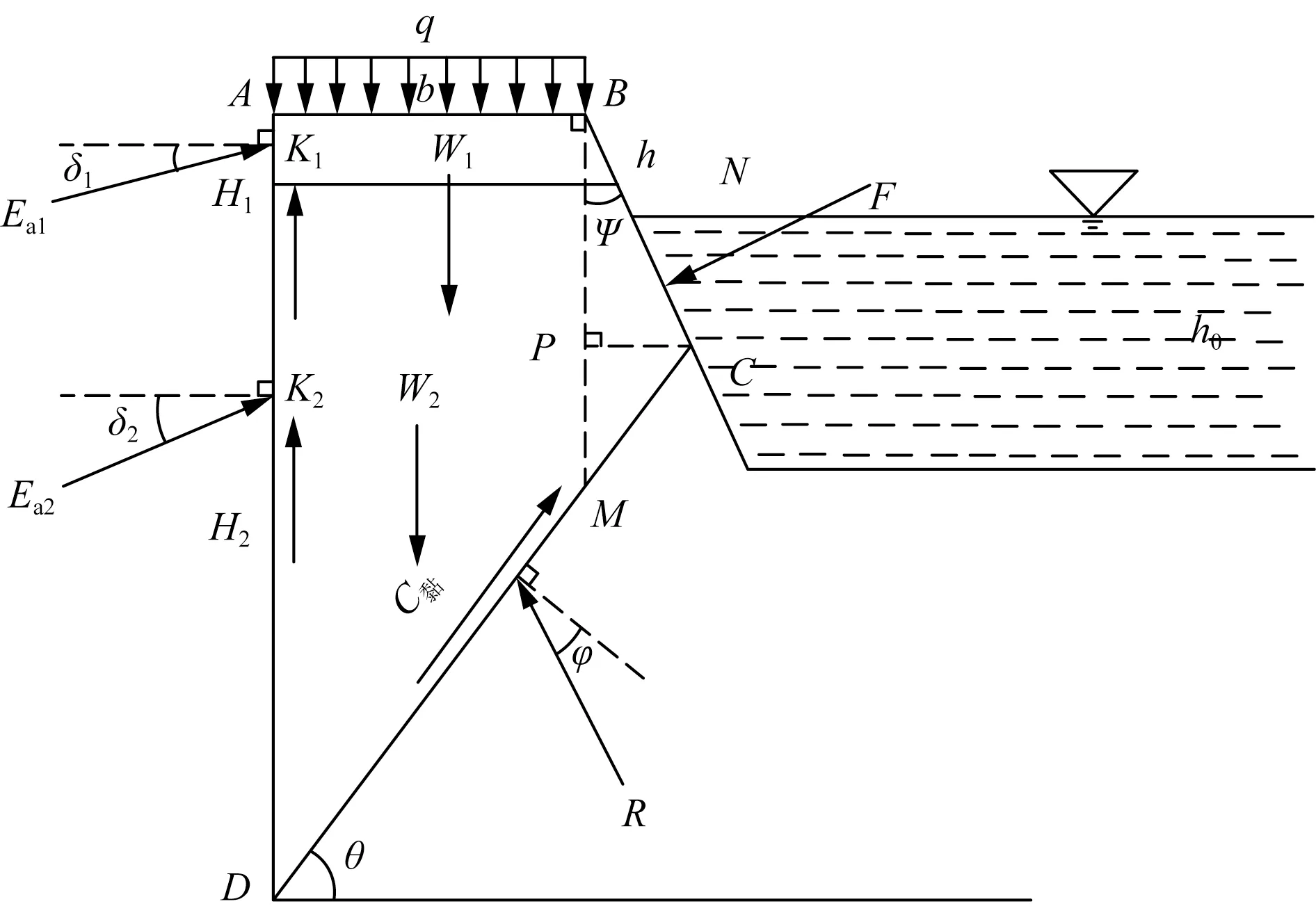
H1为上层土厚度;H2为下层土厚度;K1为上层土黏着力;K2为下层土黏着力;W1为上层土重力;W2为下层土重力;C为黏聚力;q为均布荷载;φ为内摩擦角;R为下部固定土体的抵抗力;δ1为上层土的外摩擦角;δ2为下层土的外摩擦角;Ea1为上层土主动土压力合力;Ea2为下层土主动土压力合力;x方向为水平 方向,以向右为正;y方向为竖直方向,以向下为正图2 河流所截滑裂体受力简图Fig.2 Simplified diagram of the force on the slipped body intercepted by the river

[H2-(b+T)tanθ]+(b+T)2tanθ}
(4)
式(4)中:γ2为下层土的容重。
墙土间黏着力:根据莫热菲季诺夫[13]理论,有

(5)
式(5)中:φ1为上层土的内摩擦角;c1为上层土的黏聚力。

(6)
式(6)中:φ2为下层土的内摩擦角;c2为下层土的黏聚力。
均布荷载q的作用力:
Q=qb
(7)
CD面上的黏聚力:

(8)
河流的作用范围:
CN=H-h-(b+T)tanθ
(9)
河流对河岸作用力:

(10)
以第一层土为研究对象,计算可得Ea1=0。
以第二层土为研究对象,对x方向和y方向建立平衡方程:
(11)
Ea2=[tan(θ-φ2)(W1+W2-K2-Csinθ+
Fsinψ)-Ccosθ+Fcosψ]×
[cosδ2+sinδ2tan(θ-φ2)]-1
(12)
将W1、W2、K2、C、F代入式(12),即可得到Ea2。
则总的合力为
Ea=Ea2
(13)
利用数学软件,将Ea对θ求导。当dEa/dθ=0时,Ea取得极大值,即有限成层土体的主动土压力合力,而θ即所求破裂角。在实际工程中,可以通过室内土工试验以及现场实际测量,在得到相关参数的真实值之后,将其代入dEa/dθ=0中,便可求出具体的θ值。
2)土体的破坏面被河面以上、地面以下部分所截
该情形是由于上层有限土体土层性质不稳定、开挖基坑深度较深以及上部地面活荷载过大造成的。裂缝从河面以上、地面以下部分中的某个位置生成,然后沿着基坑底部的方向逐渐扩展,并形成贯通裂缝,随着裂缝的进一步扩展、加深,最终形成滑移面。随着时间的推移,当突破某个临界点之后,土体向下开始滑动,具体受力情形如图3所示。
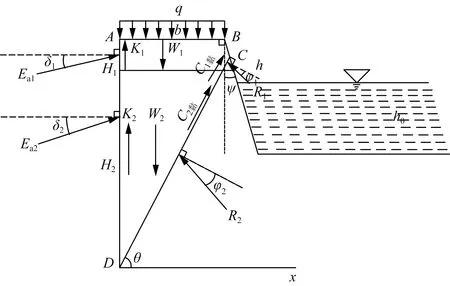
C1为上层土黏聚力;C2为下层土黏聚力;R1为上层土抵抗 力;R2为下层土抵抗力图3 被河面以上、地面以下部分所截滑裂体受力简图Fig.3 Simplified diagram of the force of the slipped body intercepted above the river surface and below the ground
其中,土层分界线与河岸的交点位于滑裂面的下方,其适用条件为
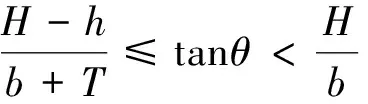
(14)
滑动土体每延米重力为

(b-H2cotθ)[H1+T(tanθ+cotψ)]}
(15)

(16)
墙土间黏着力为

(17)

(18)
均布荷载q的作用力为
Q=qb
(19)
CD面上的黏聚力为

(20)
(21)
以第一层土为研究对象,对x方向和y方向建立平衡方程:
(22)
(23)
将W1、K1、Q、C1代入式(23),即可得到Ea1。
以第二层土为研究对象,对x方向和y方向建立平衡方程:
(24)
(25)
将W1、W2、K2、C2代入式(25),即可得到Ea2。
则总的合力为
Ea=[(Ea1cosδ1+Ea2cosδ2)2]+

(26)
将Ea1和Ea2代入式(26),即可得到主动土压力合力Ea表达式。由于公式比较繁琐,此处不再赘述。借助数学软件,将Ea对θ求导。当Ea取得极值时,此时的θ即为所求破裂角,代入式(26),便能计算得出主动土压力合力Ea。
3)滑裂土体截面为三角形
该情形是由于上部有限土体土层性质较差、基坑开挖深度较深、上部受力荷载偏向一侧造成的。裂缝从水平表面的某个位置产生,然后沿着基坑底部的方向逐渐扩展,并形成贯通裂缝,随着裂缝的进一步扩展、加深,最终形成滑裂面,具体受力情况如图4所示。随着时间的推移,当突破某个临界点之后,土体向下开始滑动,其适用条件为
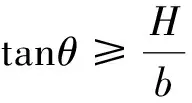
(27)
滑动土体每延米重力为
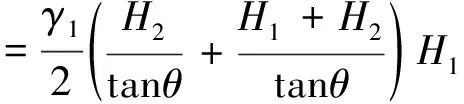
(28)
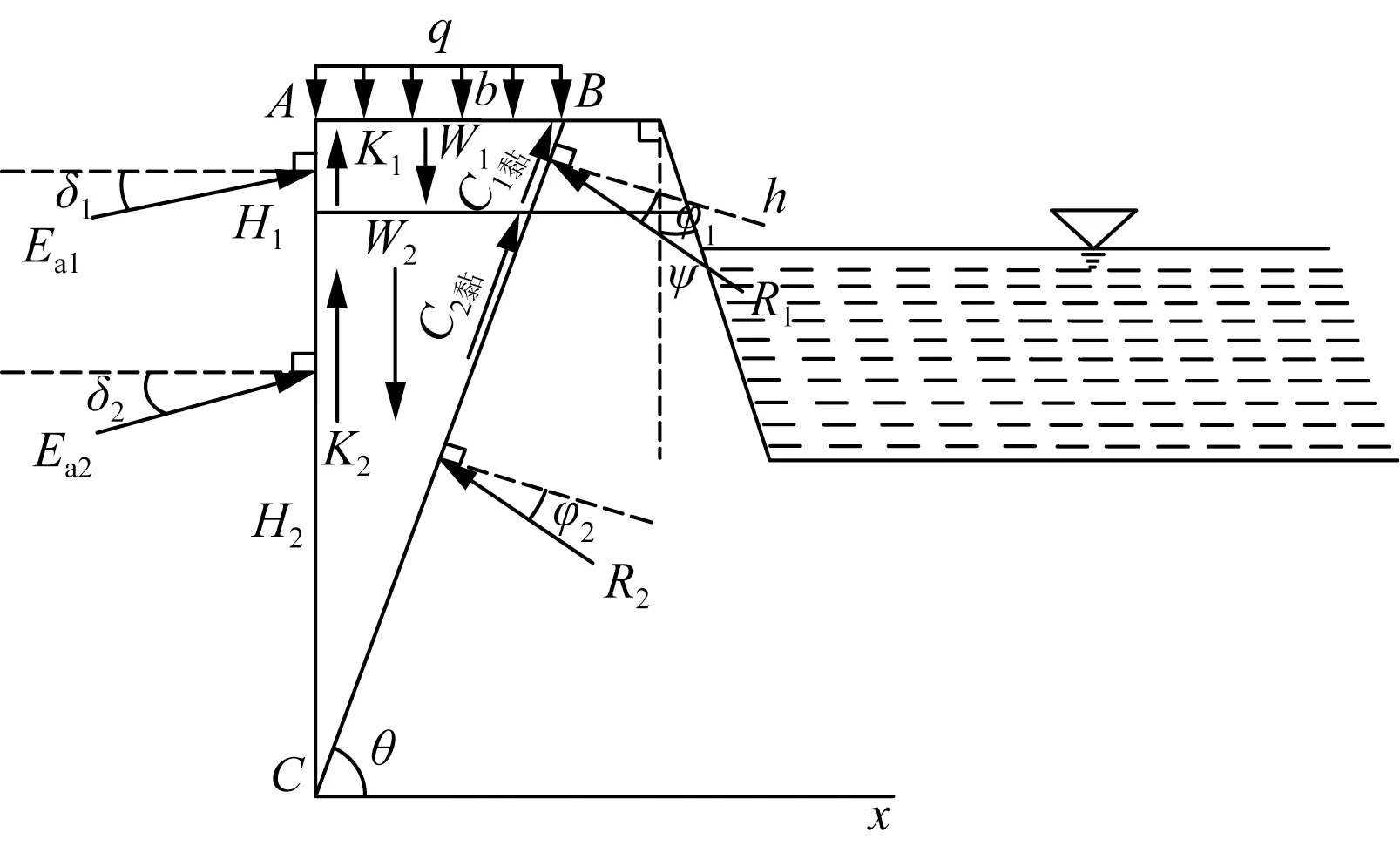
图4 三角形滑裂体受力简图Fig.4 Forced diagram of triangular slip body

(29)
墙土间黏着力为

(30)

(31)
均布荷载q的作用力为
(32)
BC面上的黏聚力:
(33)
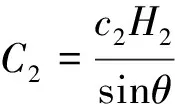
(34)
以第一层土为研究对象,对x方向和y方向建立平衡方程:
(35)
(36)
将W1、K1、Q、C1代入式(36),得
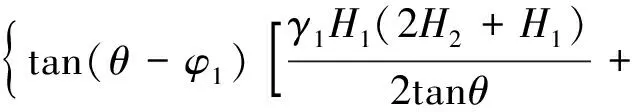
(37)
以第二层土为研究对象,对x方向和y方向建立平衡方程:
(38)
(39)
将W1、W2、K2、C2代入式(39),即可得到Ea2。
则总的合力为

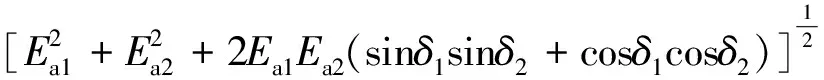
(40)
将Ea1和Ea2代入式(40),即可得到主动土压力合力Ea表达式。由于公式比较繁琐,此处不再赘述。借助数学软件,将Ea对θ求导。当Ea取得极值时,θ即所求破裂角,代入式(40),即可得到主动土压力合力Ea。
3.2 情形二:在支护结构底部滑裂
1)滑裂土体破坏面为四边形且被河流所截
该情形是由于上部有限土体不稳定、河流对河岸的冲击太大以及挡土墙埋置深度较浅造成的。裂缝从河岸坡面某个位置出现,随着水流的进入,裂缝沿着挡土墙底端的方向不断扩展、加深,最终形成贯通的滑裂面,如图5所示。其适用条件为
(41)
设CP=T0,则由S△BCM=S△BCP+S△CPM可知:
(42)

t为支护结构嵌固深度图5 被河流所截滑裂体受力简图Fig.5 Simplified diagram of the force on a fractured body intercepted by a river
则有

(43)
滑动土体每延米重力为

(44)
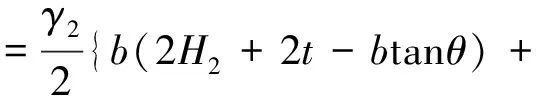
(45)
墙土间黏着力为

(46)

(47)
均布荷载q的作用力为
Q=qb
(48)
CD面上的黏聚力为
(49)
河流作用范围为
CN=H+t-h-(b+T0)tanθ
(50)
河流对河岸作用力为
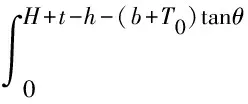
(51)
当有限土体向挡土墙发生平移或者偏转时,挡土墙受到有限土体的挤压产生位移,由于受到基坑内侧土体的限制,从而在基坑内侧产生被动土压力,用符号Ep0来表示。对于Ep0,依然可以运用极限平衡的方法,通过分析滑动体的受力情况来计算其大小,如图6所示。
滑动土体所受重力为
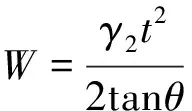
(52)
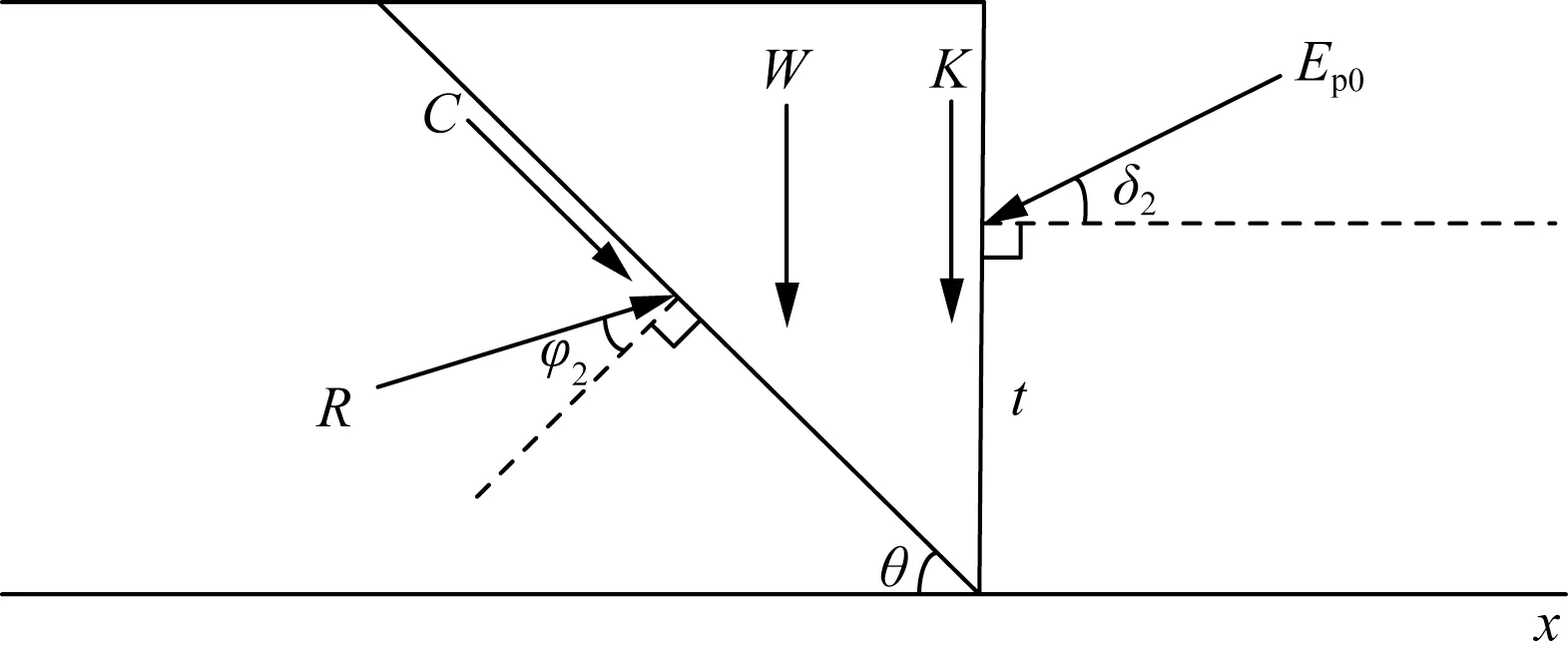
Ep0为基坑内侧土体被动土压力图6 基坑内侧滑裂体受力简图Fig.6 Simplified diagram of force on sliding body inside foundation pit
墙土间黏着力为
(53)
滑动面上的黏聚力为

(54)
对x方向和y方向建立平衡方程,即
(55)
(56)
以第一层土为研究对象,计算可得Ea1=0。以第二层土为研究对象,对x方向和y方向建立平衡方程,将W1、W2、K2、C、F、Ep0代入,即可得到Ea2。
则总的合力为
Ea=Ea2
(57)
当Ea取得极值时,θ即所求破裂角,代入式(57),便能计算出主动土压力合力Ea。
2)土体破坏面被河面以上、地面以下部分所截
如图7所示。该情形是由于上层有限土体土层性质不稳定、开挖基坑深度较深、上部地面均布荷载过大以及挡土墙埋置深度较浅造成的,其适用条件为

(58)
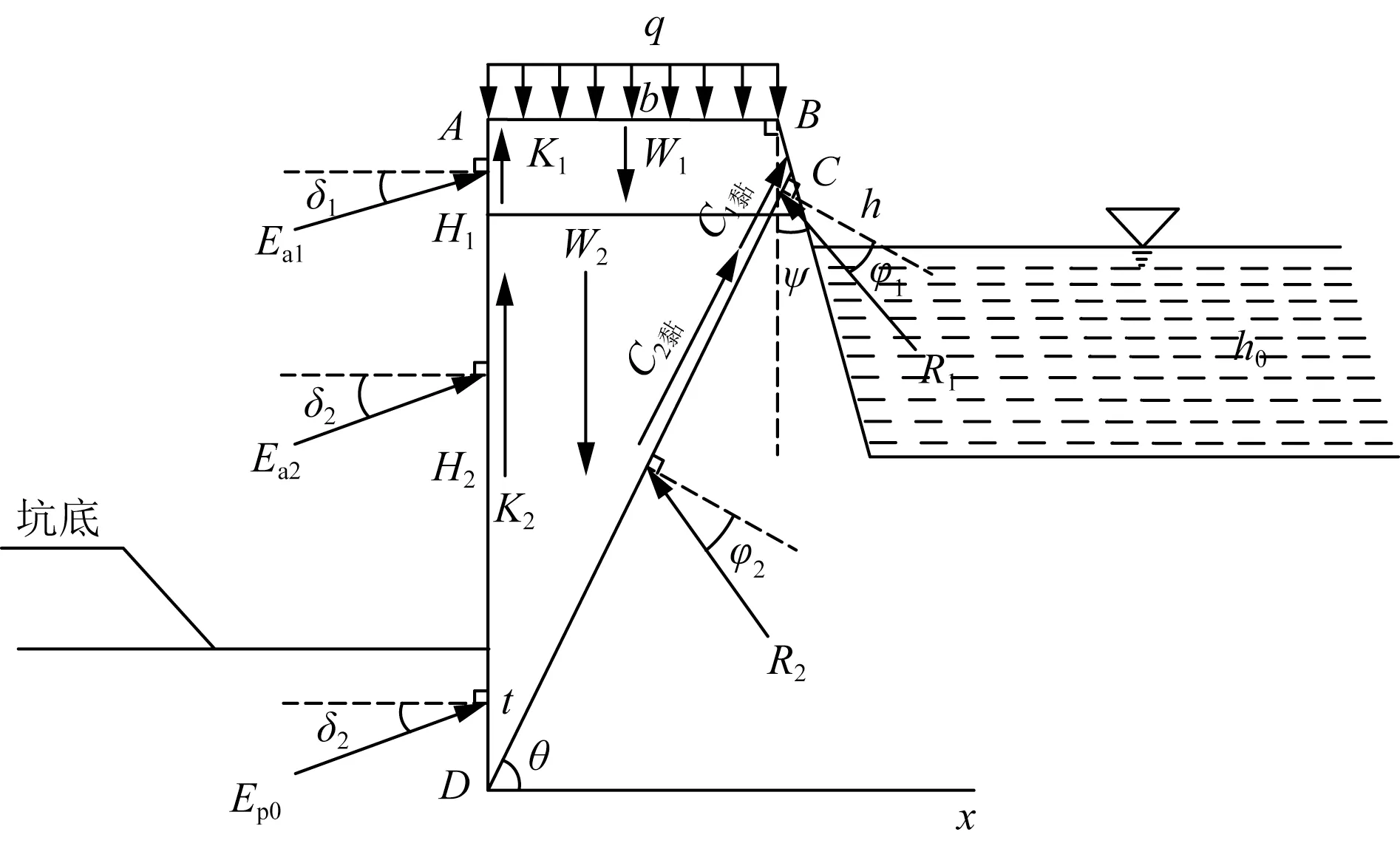
图7 被河面以上、地面以下部分所截滑 裂体受力简图Fig.7 Simplified diagram of the force of the slipped body intercepted above the river surface and below the ground
滑动土体每延米重力为

(b-H2cotθ)[H1+T0(tanθ+cotψ)]}
(59)

(60)
墙土间黏着力为

(61)
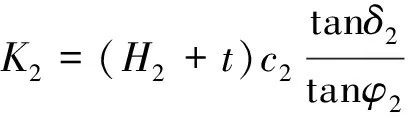
(62)
均布荷载q的作用力为
Q=qb
(63)
CD面上的黏聚力为
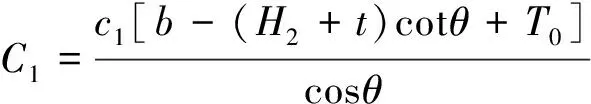
(64)

(65)
基坑内侧土被动土压力为
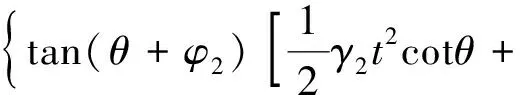
(66)
以第一层土为研究对象,对x方向和y方向建立平衡方程:
(67)
(68)
将W1、K1、Q、C1代入式(68),即可得到Ea1。
以第二层土为研究对象,对x方向和y方向建立平衡方程:
(69)
Ea2=[tan(θ-φ2)(W1+W2-Ep0sinδ2-K2-
C2sinθ)-Ep0cosδ2-C2cosθ]×
[cosδ2+sinδ2tan(θ-φ2)]-1
(70)
将W1、W2、K2、C2、Ep0代入式(70),即可得到Ea2。
则总的合力为
Ea=[(Ea1cosδ1+Ea2cosδ2)2+

(71)
将Ea1和Ea2代入式(71),即可得到主动土压力合力Ea表达式,此处不再赘述。当Ea取得极值时,θ即所求破裂角,代入式(71),即可求出主动土压力合力Ea。
3)滑裂土体破坏面为三角形
该情形是由于上层有限土体土层性质不稳定、水平地面均布荷载过大以及挡土墙埋置深度较浅造成的。裂缝从水平表面的某个位置产生,然后沿着嵌固端底方向逐渐扩展,并形成贯通裂缝,随着裂缝的进一步扩展、加深,最终形成滑裂面,具体情形如图8所示。随着时间的推移,当突破某个临界点之后,土体向下开始滑动,其适用条件为
(72)
滑动土体每延米重力为
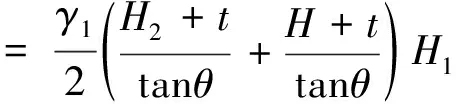
(73)
(74)
墙土间黏着力为

(75)

(76)
均布荷载q的作用力为
(77)
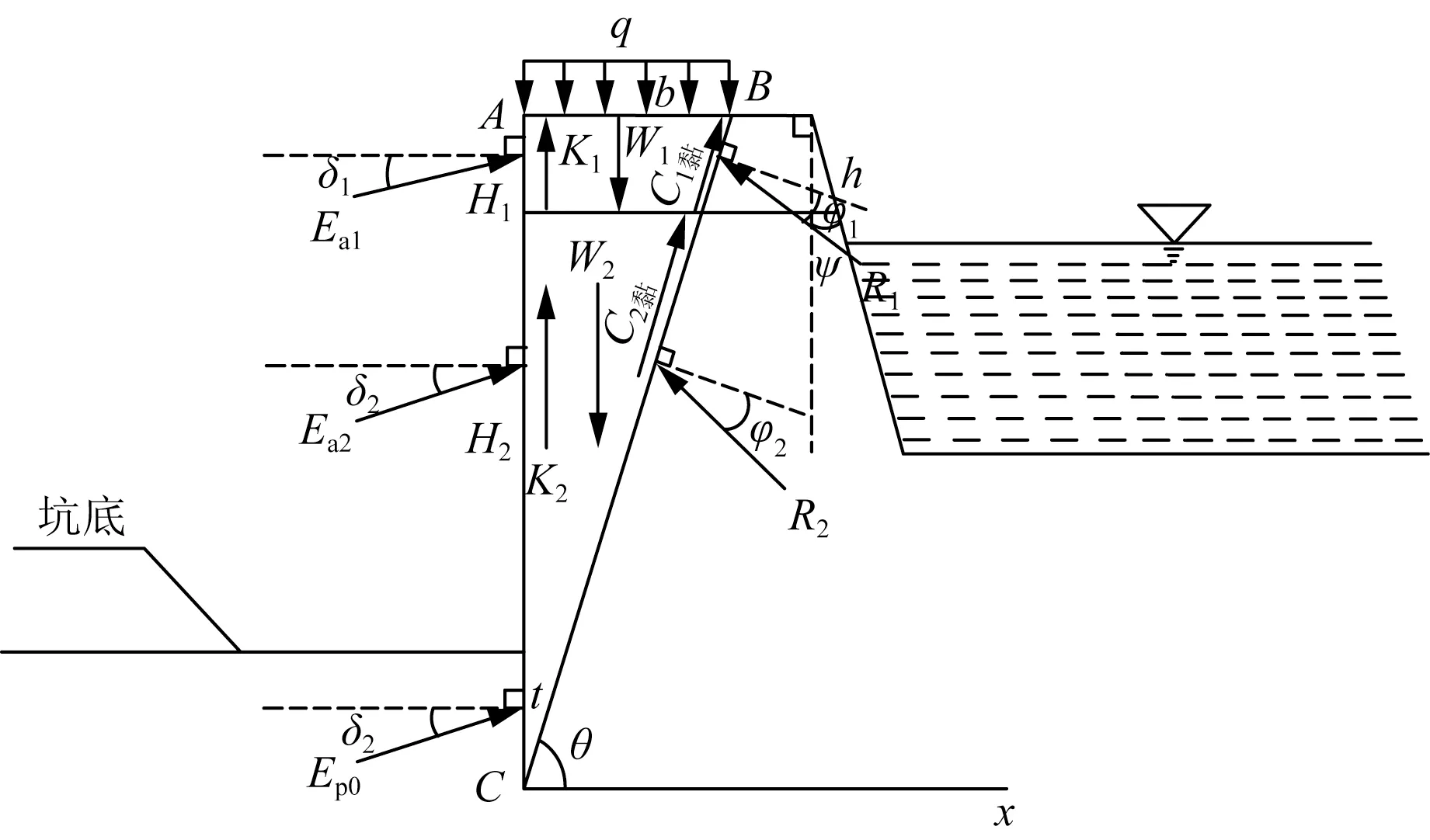
图8 三角形滑裂体受力简图Fig.8 Forced diagram of triangular slip body
BC面上的黏聚力为
(78)

(79)
基坑内侧土被动土压力为
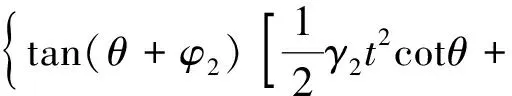
(80)
以第一层土为研究对象,对x方向和y方向建立平衡方程:
(81)
(82)
将W1、K1、Q、C1代入式(82),即可得到Ea1。
以第二层土为研究对象,对x方向和y方向建立平衡方程,将W1、W2、K2、C2、Ep0代入式(81),即可得到Ea2。
则总的合力为
Ea=[(Ea1cosδ1+Ea2cosδ2)2+
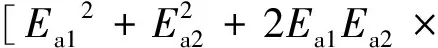
(83)
将Ea1和Ea2代入式(83),即可得到主动土压力合力Ea表达式,此处不再赘述。当Ea取得极值时,θ即所求破裂角,代入式(83),即可求出主动土压力合力Ea。
在计算完各开挖深度处的主动土压力合力后,各深度主动土压力的分布可以通过主动土压力合力的差分形式计算得出,具体公式为
(84)
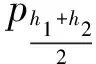
4 算例分析
以情形一为例进行算例分析。
已知某临河基坑工程,挡土墙墙后填土分为两层,上层土土层性质为:H1=1.5 m,γ1=18 kN/m3,φ1=20°,c1=5 kPa,δ1=15°;下层土土层性质为:H2=18.5 m,γ2=17 kN/m3,φ2=30°,c2=2 kPa,δ1=20°。临河距离为b=5 m,基坑开挖深度为H=20 m,河流深h0=6 m,河面离地面距离为h=2 m,土体表面均布荷载q=15 kPa,坡面与竖直方向的夹角ψ=45°。
若要计算H为10 m时的有限成层土体主动土压力合力,先将各参数代入式(13),经数学软件计算可知,当dEa/dθ=0时,得θ=54.99°,tanθ=1.43,由于(H-h)/(b+T)=1.29,[H-(h+h0)]/[b+(h+h0)tanψ]=0.15,tanθ=1.43∉[0.15,1.29),所以此种情况不满足式(1);再将各参数代入式(26),经数学软件计算可知,当dEa/dθ=0时,得θ=55.0°,tanθ=1.39,由于(H-h)/(b+T)=1.29,H/b=2,tanθ=1.43∈[1.29,2),所以此种情况满足式(14),将θ代入式(26),求得有限成层土体主动土压力合力为113.1 kN/m。
表1列出了本文方法与朗肯理论在各深度处的主动土压力合力数值。
将两种方法所得主动土压力合力数据绘制成曲线图,如图9所示。

表1 两种方法所得各深度处的主动土压力合力对照表Table 1 Comparison table of the resultant active earth pressure at each depth obtained by the two methods
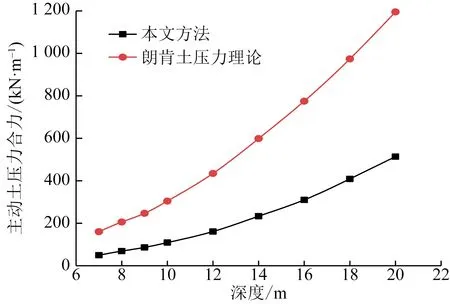
图9 两种方法所得主动土压力合力对比图Fig.9 Comparison chart of the resultant active earth pressure obtained by the two methods
由图9可知,本文所用方法与朗肯计算法所得主动土压力随深度变化曲线发展趋势大致相同。在基坑开挖深度较浅时,两种方法所得主动土压力合力相差较小,当开挖到坑底时,两者差距较大。但我们也注意到,在基坑开挖前期,朗肯主动土压力合力是本文方法所得主动土压力合力的3.2倍,到了开挖结束时,前者是后者的2.3倍。这说明当基坑开挖过深时,无论何种土压力计算方法都会受到开挖深度的影响而产生偏差,与实际情况存在出入。
考虑土体表面荷载q对有限成层土体主动土压力合力的影响,依次取q=10、20、30 kPa,计算所得数据如图10所示。
由图10可知,随着土体表面均布荷载逐渐增大,有限成层土体主动土压力合力也随之增大,但同时我们也注意到土压力合力随着深度的增长趋势基本一致。这说明土体表面均布荷载并不会对有限成层土主动土压力的增长趋势产生影响,仅仅只是数量的增减。
在分析临河距离b对有限成层土体主动土压力合力的影响时,依次取b=4、5、6、7、8 m,其他参数保持不变,计算所得数据如图11所示。
由图11可知,在基坑开挖深度较浅时,有限土体主动土压力合力比较接近,这说明开挖基坑临河距离对于较浅的开挖基坑影响较小,而随着基坑深度的增加,不同开挖基坑临河距离对应的有限土体主动土压力合力差距逐渐加大。开挖基坑临河距离越大,相应的有限土体主动土压力合力越大。在超过一定的深度后,曲线呈现平行态势,这说明不同开挖基坑临河距离对于有限土体主动土压力合力的影响趋于稳定,不会产生较大的波动。
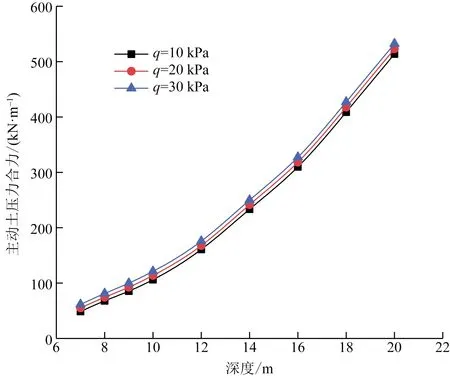
图10 不同表面荷载对应的主动土压力合力 随深度变化曲线Fig.10 The curve of the resultant force of active earth pressure corresponding to different surface loads with depth
当考虑嵌固深度t对有限土体主动土压力合力的影响时,分别取t=3、4、5、6 m,计算所得数据如图12所示。
从图12可以发现,主动土压力合力与嵌固深度呈正相关,后者增大,前者也随之增大;后者减小,前者也随之减小。同时,当基坑开挖深度超过一定数值时,嵌固深度对于主动土压力合力的影响将特别显著,在开挖基坑较浅时,嵌固深度对于主动土压力合力的影响相对较小。

图11 不同临河距离对应的主动土压力合力 随深度变化曲线Fig.11 The curve of active earth pressure resultant force with depth corresponding to different riverside distances
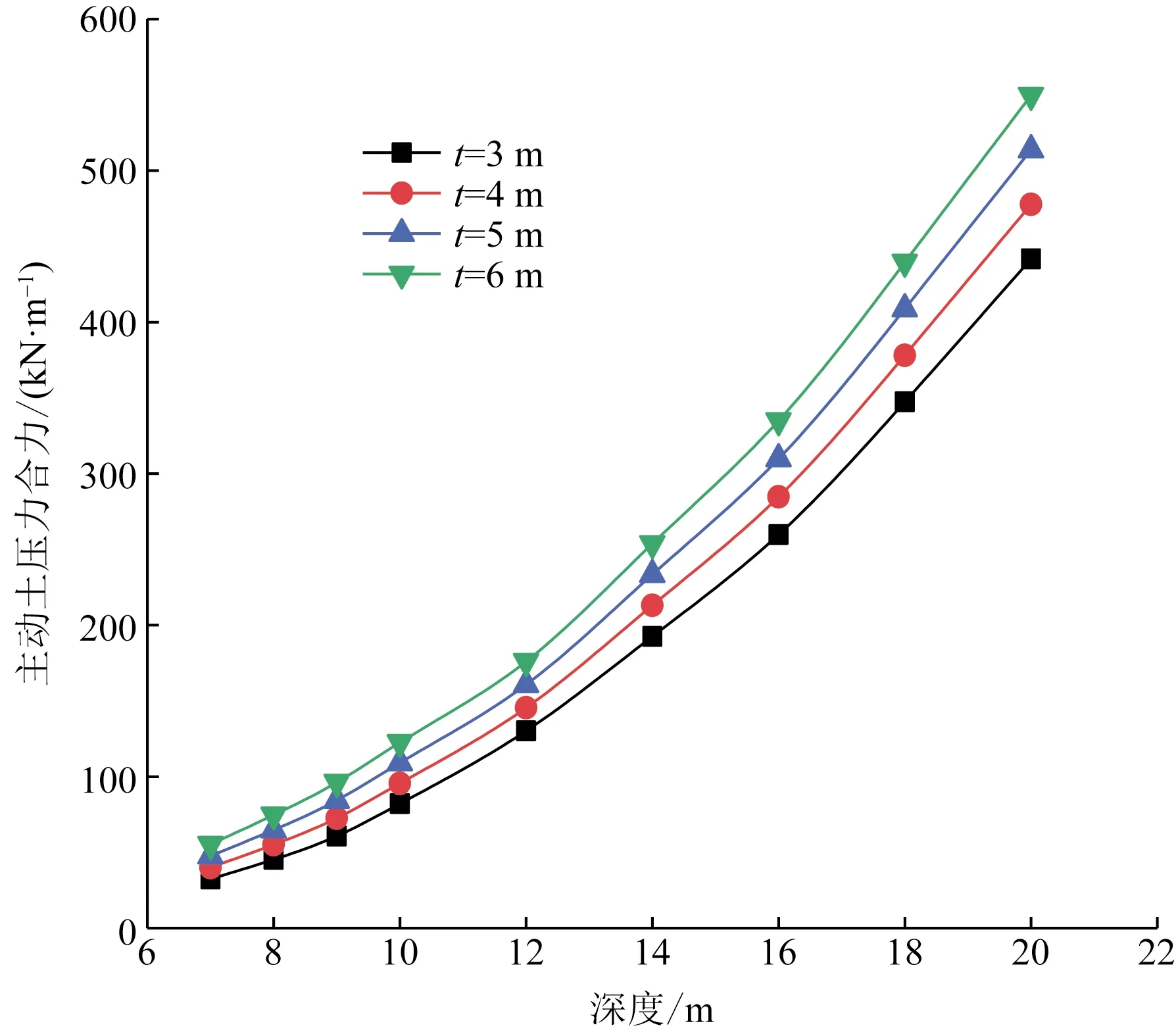
图12 不同嵌固深度对应的主动土压力合力 随深度变化曲线Fig.12 The curve of active earth pressure resultant force with depth corresponding to different embedded depths
5 结论
以临河的开挖基坑与河流之间的有限土体作为研究对象,通过研究有限土体滑裂面的不同情况,来探讨临河基坑有限成层土体主动土压力的大小。在分析的过程中,考虑了多种作用力的影响,从而得出了更加完备的主动土压力公式。最后,通过算例分析验证了公式的正确性。在与朗肯主动土压力公式对比后,得出如下结论。
(1)随着土体表面均布荷载逐渐增大,有限成层土体主动土压力合力也逐渐增大,但增长趋势基本相同。
(2)开挖基坑临河距离对于较浅的开挖基坑影响较小,而随着基坑深度的加深,不同开挖基坑临河距离对应的有限土体主动土压力合力差距逐渐增大。开挖基坑临河距离越大,相应的有限土体主动土压力合力越大。在超过一定的深度后,临河距离对被动土压力合力的影响趋于稳定。
(3)分层土条件下的主动土压力合力与嵌固深度呈正相关,同增同减。同时,基坑开挖越深,嵌固深度对于主动土压力合力的影响也越显著,在开挖基坑较浅时,嵌固深度对于主动土压力合力的影响相对较小。
