基于铁塔等效的交叉跨越架空线安全距离分析
2022-02-18朱登杰廖永力唐捷黄志都李锐海黄增浩张志强
朱登杰, 廖永力, 唐捷, 黄志都, 李锐海, 黄增浩, 张志强
(1.南方电网科学研究院有限责任公司, 广州 510000; 2.广西电网有限责任公司电力科学研究院, 南宁 530000)
近年来,中国的输电线路里程数迅速增长,线路走廊日趋紧张,出现了许多交叉跨越线路[1]。与普通输电线路相比,交叉跨越线路的安全性要求更高[2]。在风载荷作用下,相互交叉线路间的电气安全距离由于导地线的运动会发生动态变化,对于高电压等级的交叉跨越线路,在极端大风天气影响下可能会出现交叉跨越线路风偏闪络。为保障交叉跨越线路安全运行,许多学者对交叉跨越架空线距离的测量方法进行了研究[3]。卞玉萍等[4]针对输电线路跨越其他线路等现场情况,提出了一套测量跨越距离的新公式和方法。韩晓坤[5]为了提高测量效率和即时性,将机器视觉应用于输电线路交叉跨越距离测量当中,提升了测量的效率和即时性。而对交叉跨越线路的仿真模拟研究则较少,庞锴等[6]建立了交叉跨越线路的三塔四线有限元模型,重点研究动态风荷载作用下交叉跨越线路金具的受力情况。
许多研究使用有限元方法计算绝缘子风偏和架空线动态响应,刘小会等[7]在ABAQUS软件中建立了500 kV超高压线路的多体导线模型,并进行了模型在脉动风速作用下的时程分析,研究风偏角的计算结果。Yan等[8]建立了一个输电线路耐张段的线-绝缘子有限元模型,以模拟悬垂绝缘子串的动态摆动。实际工程中的导线悬挂于输电铁塔和绝缘子串上,并受到相邻跨导线的影响,在分析研究中这些因素可通过在导线挂点施加等效弹簧进行模拟。霍涛等[9]的理论分析结果显示,导线两端的边界条件对导线舞动的竖向幅值有较明显的影响。输电铁塔在大风工况下发生的变形以及铁塔本身的刚度会影响导线两端的边界条件,有必要在分析架空线位移时程时建立完整的塔线体系模型[10]。
精细的输电铁塔有限元模型虽能准确反映结构的力学特性,但计算量巨大。尤其在进行多档输电线路的建模和计算时,符合工程精度的输电铁塔等效计算方法有着良好的应用价值。朱伯文[11]结合一种将格构式钢架等效为薄壁结构的方法,考虑拉压刚度、弯曲刚度、扭转刚度以及附加质量4个方面,提出了一种将格构式铁塔简化为梁柱模型的方法。作者对比精确和简化的有限元模型在静力作用下的变形、固有频率及振型、时变风荷载下的位移时程及其频谱,验证了简化模型的正确性。李吉林[12]使用等效梁柱法对自立式杆塔进行了简化。对比结果表明简化模型与精确模型在静力特性与固有频率两方面具有较好的一致性。杨文刚等[13]使用等效简化模型建立自立式铁塔塔-线体系模型,并模拟了脱冰跳跃工况下塔线体系的动态响应,验证了铁塔等效简化方法在动态响应计算中的有效性。
工程实际中为保证重要交叉跨越线路的安全运行,在台风、龙卷风等极端天气时,需要开展重要交叉跨越线路安全性实时评估和预警,以提高计算效率,在满足工程精度要求的同时,保证计算的实时性。因此,现基于输电铁塔刚度等效,简化铁塔有限元模型,提出等效的交叉跨越塔线体系有限元模型的方法;针对一220 kV交叉跨越线路,对输电铁塔进行刚度等效,从静力变形、振型和固有频率方面对等效模型进行验证。最后根据架空线关键节点位移结果校验了该交叉跨越线路在大风工况下的安全距离。
1 交叉跨越架空线动态安全距离分析模型
利用塔线体系有限元模型分析动态线间距离的具体过程如图1所示。首先建立塔线体系有限元模型,在对模型施加动态载荷之后进行瞬态分析,得到节点位移时程,根据规范判断架空线之间的距离是否安全。
分析过程中的动态响应求解部分要耗费大量计算时间。输电铁塔刚度等效方法能显著减少铁塔有限元模型的单元数量,若将铁塔等效模型应用于塔线体系建模,则可以大大缩短分析所需时间。

图1 交叉跨越架空线动态安全距离分析流程Fig.1 The calculation process of the safe distance for crossover overhead lines
2 输电铁塔桁梁模型与等效模型
2.1 输电铁塔桁梁模型的建立
根据设计图纸,在ANSYS软件中建立自立式输电铁塔的桁梁模型。主材以及承受弯矩和扭矩斜材使用BEAM188单元,只承受轴向作用的斜材、辅材的单元类型为LINK180,单塔模型共有1 132个单元。模型材料为Q345,弹性模量2.06×1011Pa,泊松比0.3,密度7 850 kg/m3。最终模型如图2所示。
2.2 输电铁塔塔身刚度与质量等效
考虑铁塔结构的等效拉压刚度时,由于格构式铁塔塔段所用的主材规格比斜材大得多,主材对结构整体拉压刚度的贡献值远大于斜材。当忽略斜材的拉压刚度时,输电铁塔塔段等效拉压刚度EAeq可表示为
EAeq=EAlegs=E(A1+A2+A3+A4)
(1)
式(1)中:E为角钢材料的拉伸弹性模量;Aeq为梁柱单元的等效截面积;A1~A4分别为编号1~4的主材角钢各自的截面积;Alegs为主材角钢的截面积之和。
考虑铁塔的等效弯曲刚度时,由于输电铁塔主材的角钢截面惯性矩显著大于斜材,在进行等效计算时可只考虑主材截面惯性矩。根据图3所示的截面示意图,x向和y向的弯曲刚度可分别表示为
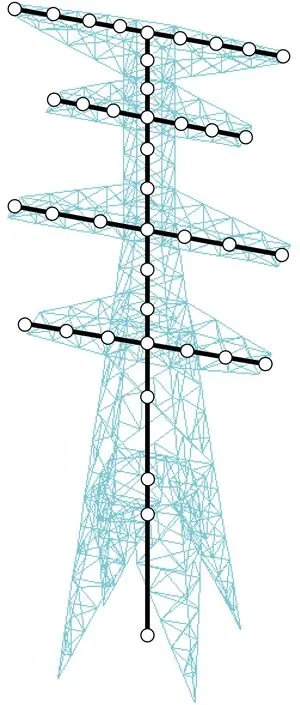
图2 自立式输电铁塔桁梁模型与等效模型Fig.2 Truss-beam model and equivalent model of self-supporting transmission tower
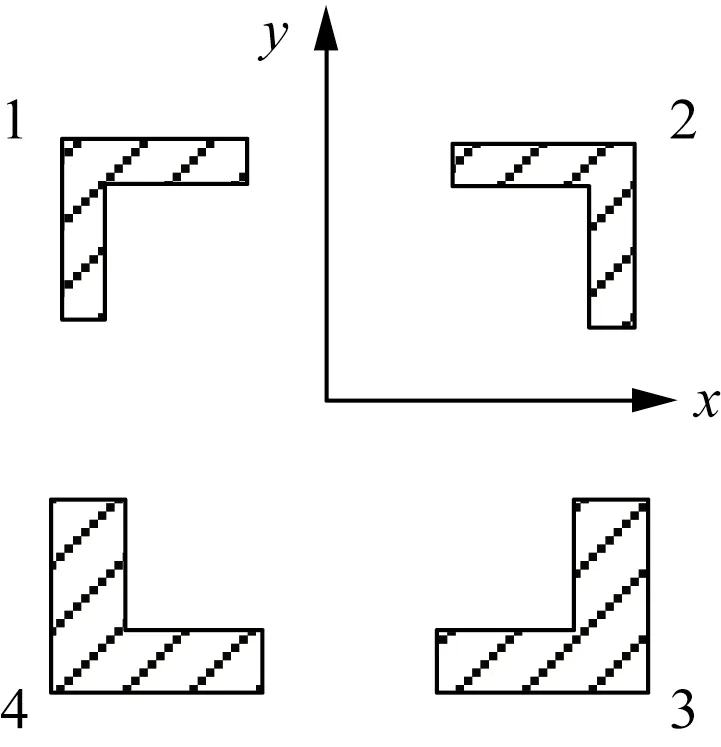
图3 塔段截面示意图Fig.3 Schematic diagram of tower section
(2)
式(2)中:Ieq为等效截面惯性矩;Ii为主材角钢相对截面惯性矩,其中,i=1,2,3,4。
Ii=Ii0+AB2
(3)
式(3)中:Ii为单根主材相对塔段截面中性轴的惯性矩;Ii0为角钢相对于自身中性轴的惯性矩;A为角钢截面积;B为构件弯曲中性轴到整体截面中性轴的距离,取塔段宽度(b)的一半,即B=b/2。
将输电铁塔结构等效为薄壁结构并计算其扭转刚度,文献[14]利用应变能相等的思想将承受扭矩的格构式结构等效为薄壁结构(图4),其等效厚度t的计算公式为
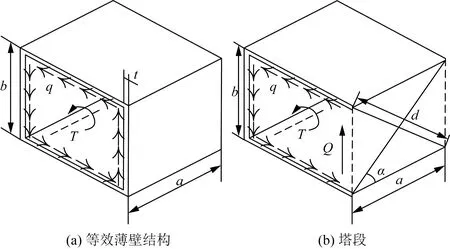
T为扭矩;q为剪力流;Q为剪力;α为斜材倾斜角图4 塔段薄壁等效示意图Fig.4 Schematic diagram of thin-wall equivalence
(4)
式(4)中:E为材料的弹性模量;G为材料的剪切模量;a为一个节间的长度;d为斜材的长度;Ad为斜材的截面积;Al为主材的截面积。根据闭口薄壁杆的扭转变形理论,上述四边形截面铁塔结构的等效扭转刚度GJeq可表示为
GJeq=Gb3t
(5)
在计算等效拉压刚度时,只考虑了塔段主材,而忽略了斜材与辅材。若直接按等效拉压刚度计算所得的截面积和一般钢材的密度建立等效梁,则未考虑斜材与辅材的质量,等效梁的质量与塔段的实际质量相差较大。为保证等效梁质量与对应塔段总质量一致,根据设计图纸中标注的塔段角钢总质量与等效梁的几何尺寸反算等效梁应有的密度,并在建立等效模型时使用该特殊密度。
根据铁塔结构设计图,将铁塔每一个X或Z型编花的部分划分为一个塔段,全塔共分为43个部分。根据第1节所述的方法,对铁塔的每一个结构分段进行等效参数(等效截面积、等效截面弯曲惯性矩、等效截面扭转惯性矩以及等效质量)的计算。根据等效计算结果,在ANSYS软件中建立自立式输电铁塔的等效模型。使用BEAM188单元,选用自定义梁截面,根据等效计算结果赋予自定义截面对应的参数。设置材料参数为:弹性模量2.06×1011Pa,泊松比0.3,密度根据等效质量计算结果设置。
2.3 等效模型静态特性与模态特性验证
为验证等效模型在静态与动态特性方面与桁梁模型的一致性,对比了两种模型在自重条件下、受顺线路方向载荷两种情况下塔身节点的位移,图5为变形示意图,位移及其误差如图6所示。
对桁梁模型与等效模型进行模态分析,两种模型的振型如图7所示,其固有频率结果如表1所示。

图5 桁梁模型与等效模型的变形Fig.5 Deformation of two models

图6 桁梁模型与等效模型的位移与误差Fig.6 The displacement and error of the beam model and the equivalent model

表1 两种模型固有频率对比Table 1 Natural frequencies of two models
在静态力作用下,铁塔等效模型的位移与桁梁模型位移结果的误差多在10%以内,最大误差不超过13%,表明等效模型的静态特性与桁梁模型具有较好的一致性。等效模型的前三阶振型与精确模型相同,固有频率误差也在7.5%以内,表明两者的动态特性也具有较高的相似度。
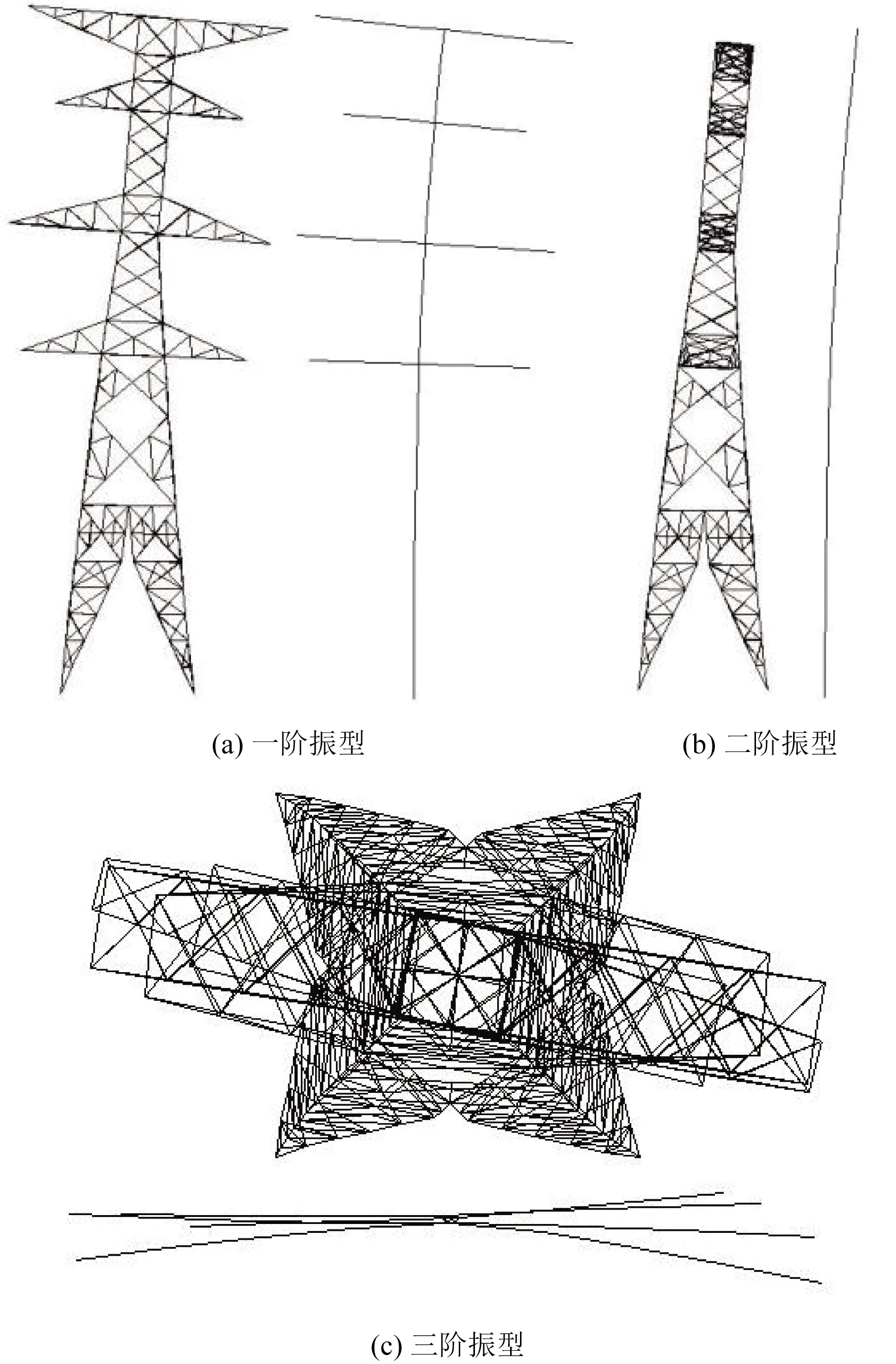
图7 桁梁模型与等效模型的振型Fig.7 Mode shapes of two models
3 脉动风激励下交叉跨越线路动态响应分析
3.1 交叉跨越塔线体系建模
本文研究中一处220 kV交叉跨越线路,上方线路铁塔呼高45 m,档距244.5 m,两基铁塔均为直线塔;下方线路铁塔呼高18 m,档距482 m,包括一基终端塔和一基耐张塔,两条线路夹角90°。输电铁塔模型依据第2节所述的原则建立,架空线和绝缘子串使用杆单元模拟,绝缘子与架空线、铁塔之间的连接等效为理想球铰,使用迭代找形法[15]确定了架空线在自重作用下的初始形态和初始张力。根据文献[16]的数据,塔线体系结构的阻尼比取0.025。在ANSYS软件中建立的交叉跨越塔线体系模型如图8所示。
换用铁塔等效模型,使用相同的坐标建立等效之后的交叉跨越有限元模型。两种模型除了铁塔模型的形式不同之外,挂线点坐标、档距、导地线参数、绝缘子参数等其他模型参数完全一致。
3.2 大风载荷激励下架空线节点位移对比
考虑45°方向大风作用下交叉跨越线路的动态响应,根据Davenport风谱,使用谐波叠加法[17]生成600 s的脉动风速时程,并根据规范[18]中的公式计算风载荷。脉动风模拟使用的主要参数为:时间步长0.1 s,截止频率4.8 Hz,频率划分数8 192。根据设计资料,取10 m高度平均风速31 m/s。在选取架空线载荷模拟点时,由于每档架空线均匀划分为60个单元,每隔20个节点归为一个风速段,取该段中点作为风荷载模拟点,风速段内的所有节点均取该点的模拟结果作为脉动风速;铁塔上则根据塔身横隔面的位置,将铁塔分为5个风载荷加载段,每段根据横隔面中点的脉动风速模拟结果来换算载荷。

图8 交叉跨越线路有限元模型Fig.8 Finite element model of crossover transmission line
施加时变风荷载之后,对传统桁梁模型和等效模型塔线体系分别进行了瞬态响应计算,分别提取桁梁模型和等效模型架空线档距中点的竖向(y)位移时程,曲线绘制如图9所示,可见等效模型与桁梁模型在架空线中点位移时程曲线上十分接近。分别计算了两种模型架空线位移的均值和极值,结果如图10所示。可知两种模型计算得到的架空线节点位置均值误差在2%以下,极值误差也在3.3%以下,在分析架空线位移时程和安全距离时,可以使用等效模型替代桁梁模型。
3.3 等效模型在计算成本方面的优势
由3.2节可见,等效模型计算得到的架空线位移时程与桁梁模型十分接近,而在单元数量、计算时间和结果文件体积方面,等效模型有显著优势。等效模型塔线体系共有2 081个单元,单元数量与精确模型相比减少了约77%;同样使用Intel Core i5-6500处理器,桁梁模型塔线体系计算600 s动态响应耗时约6.78 h,而等效塔线体系模型计算耗时约0.87 h,节省了约87%的计算时间;生成的结果文件体积也缩减91%,从121 GB缩减至11.1 GB,两种模型计算成本对比如图11所示。
3.4 利用等效模型校验架空线安全距离
主要考虑两条交叉线路之间的安全距离问题,跨越位置附近的架空线之间最易出现距离不足,根据GB50545中110~750 kV架空输电线路设计规范[19],220 kV电力线路交叉时最小垂直距离4 m,两平行线路接近时最小水平距离7 m,故在交叉位置附近以架空线外侧7 m左右(向更远处取到节点位置)的范围选定关键节点。该范围外的节点水平距离都在规定值以上,不会有闪络危险,仅考虑范围内节点的垂直距离即可。上方线路关键节点编号为1404~1412、1585~1593,下方线路关键节点编号为38~42、99~103,如图12所示。
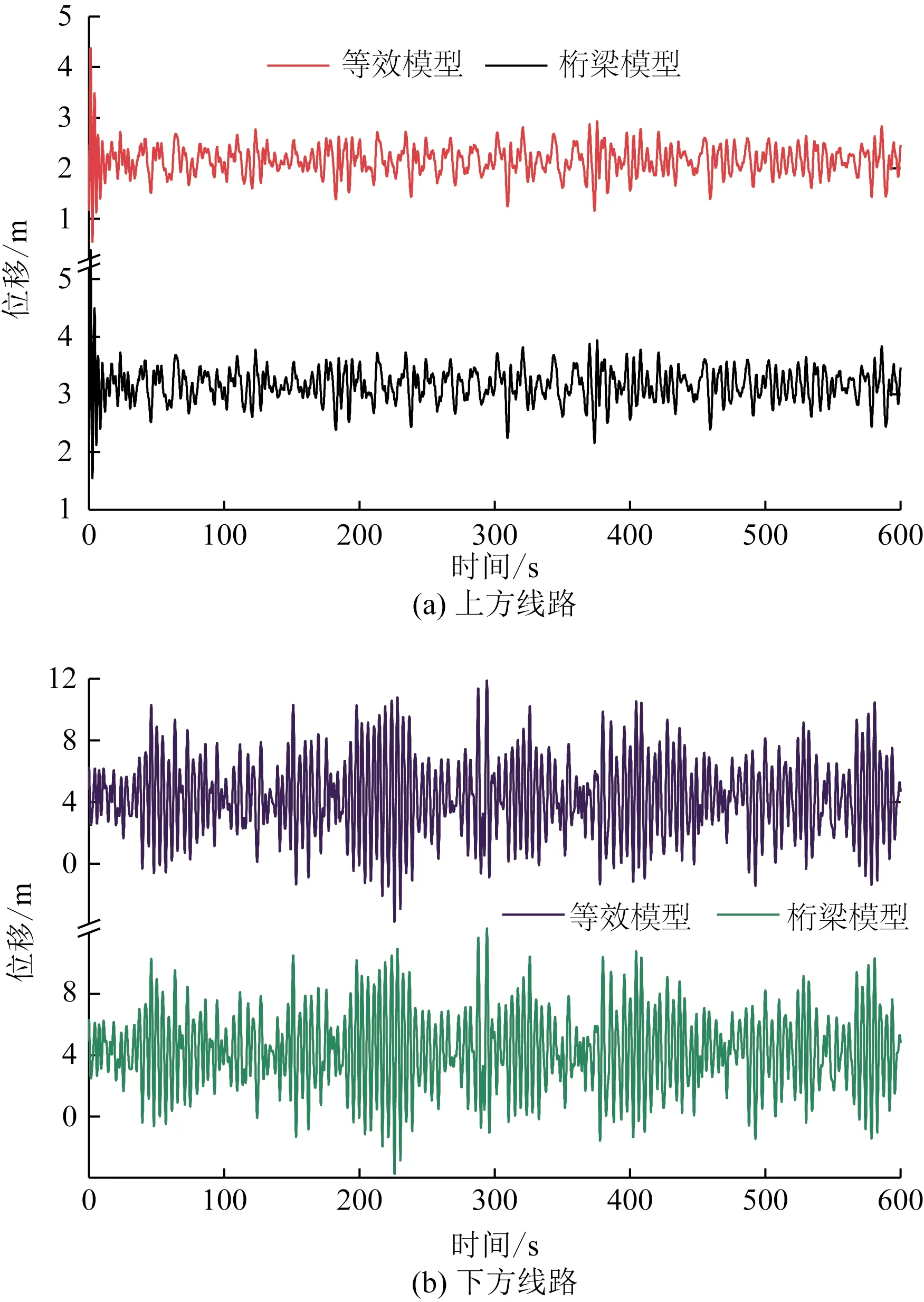
图9 两种模型架空线中点位移时程曲线Fig.9 Displacement time history curve of middle nodes on the two models

图10 两种模型关键节点位移对比与误差Fig.10 Displacement comparison and error of key nodes of the two models
结合架空线初始位置和动态时程曲线,计算上下两层线路关键节点在动态风荷载的激励下的垂直距离。某时刻的线路垂直间距为该时刻上、下层架空线关键节点中最低点、最高点的Y坐标作差,计算结果如图13所示。
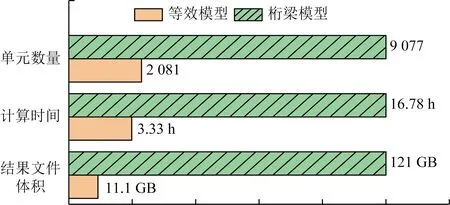
图11 等效模型与桁梁模型计算成本对比Fig.11 Comparison of computation costs

图12 交叉位置关键节点 Fig.12 Key nodes at cross position
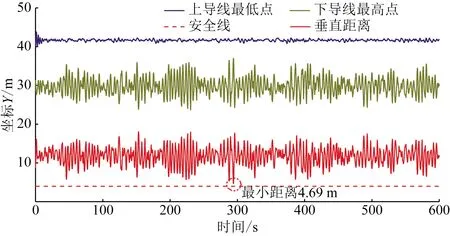
图13 交叉跨越架空线关键节点最值和最小垂直距离Fig.13 Extreme displacement values of crossover lines and the minimum vertical distance
由图13可知,跨越线路最小垂直距离为4.69 m,没有超过规范规定的最小距离4 m,但是比较接近,存在闪络的可能性,有必要加强实时监测,以确定合理运行方式,保障电网安全。
4 结论
(1)根据输电铁塔主材截面参数,对铁塔结构进行了拉压刚度、抗弯刚度、扭转刚度的等效计算,建立了220 kV交叉跨越线路的等效塔线体系模型。通过对比分析,发现等效铁塔模型在静态受力和模态特性方面与桁梁模型具有良好的一致性。
(2)有限元模型的瞬态计算结果表明,使用等效模型计算得到的架空线节点位移与桁梁模型结果具有较好的一致性,可以使用等效模型分析脉动风激励下交叉跨越线路的安全距离,该等效方法可减少约77%的单元数量,节省约87%的计算时间。
(3)通过对跨越线路关键节点竖向位移时程的分析,发现该跨越线路在平均风速31 m/s的脉动风载荷作用下,上下两层线路之间的距离在规范规定的4 m以上,符合线路安全运行标准。
