General interaction quenches in a Luttinger liquid

You-Ming Wei and Hantao Lu

1 School of Physical Science and Technology&Key Laboratory for Magnetism and Magnetic Materials of the MoE, Lanzhou University, Lanzhou 730000, China

2 Lanzhou Center for Theoretical Physics, Key Laboratory of Theoretical Physics of Gansu Province,Lanzhou University, Lanzhou, Gansu 730000, China

Abstract We discuss a general interaction quench in a Luttinger liquid described by a paired bosonic Hamiltonian.By employing su(1, 1) Lie algebra, the post-quench time-evolved wavefunctions are obtained analytically, from which the time evolution of the entanglement in momentum space can be investigated.We note that depending on the choice of Bogoliubov quasiparticles,the expressions of wavefunctions, which describe time-evolved paired states, can take different forms.The correspondence between the largest entanglement eigenvalue in momentum space and the wavefunction overlap in quench dynamics is discussed,which generalizes the results of Dóra et al(2016,Phys.Rev.Lett.117,010 603).A numerical demonstration on an XXZ lattice model is presented via the exact diagonalization method.

Keywords: quantum quench, exact diagonalization, Luttinger liquid, XXZ model

1.Introduction

Quantum quench, where parameters in the Hamiltonian are changed discontinuously to leave a system out of equilibrium,is an important subject in the study of nonequilibrium dynamics of isolated quantum systems [1, 2].Though the problem is well defined,most of the known exact results essentially come from noninteracting systems, e.g.the transverse-field Ising model[3,4],and some pairing models[5–7].For many-body systems the situation is much more complicated, and generally completely exact treatments are far beyond reach even for relatively simple models [8–10].In order to procure some qualitative understandings and to make decent quantitative predictions, we usually have to resort to effective theories.

Analogous to the prevalent Landau’s Fermi liquid theory,a bunch of one-dimensional (1D) quantum systems can be classified into a universal category known as Luttinger liquids[11–13], where only a handful of parameters are sufficient to address the low-temperature properties of systems effectively.A bit of a surprise is that within the framework of the Luttinger liquid theory, it is possible to produce highly accurate descriptions on the nonequilibrium dynamics of the systems in their gapless (critical) phases.This observation has been justified by numerical computations on various lattice models [14, 15].

One advantage of the investigations from the effective theory side is that analytical approaches, in many cases, can be carried out at least approximately[16,17].In the work of Dóra et al[18],based on the analysis of an effective Luttinger Hamiltonian, an interesting observation was made, which unveiled the correspondence between the time-evolved entanglement spectrum and the nonequilibrium characteristics in the quench dynamics,including the identification of the largest momentum-space entanglement eigenvalue and the Loschmidt echo.In their work,the correspondence was made plain first via the calculations on the simple Luttinger liquid Hamiltonian,and later was ratified by the numerical results on spin-chain lattice models.In our opinion,the work highlights the effectiveness of the Luttinger liquid theory in the nonequilibrium dynamics of 1D critical systems.

Nevertheless, in the paper [18] the authors discussed primarily the noninteracting-to-interacting quenches, leaving the issue of general quenches untouched, e.g.a quench from one nonzero coupling strength to another.In this study, we would like to address the quench dynamics of the Luttinger liquid model in more general settings, by investigating the quenches that can start from an arbitrary (interacting) ground state(GS).With the assistance of su(1,1)algebra,we procure the exact expression of the time-evolved wavefunction, and obtain the largest entanglement eigenvalue in momentum space accordingly.We note that the correspondence raised in[18] can be generalized consequently.We confirm it numerically in the XXZ-related model (see (31) for the Hamiltonian), which is a lattice realization of the Luttinger Hamiltonian(1).There we find that the agreement holds in the sense that the largest momentum-space entanglement eigenvalue coincides with the overlap of the time-evolved wavefunction with its noninteracting GS,rather than with the initial interacting GS from which the quench starts.

The rest of the paper is organized as follows.After an introduction of the Luttinger liquid Hamiltonian in terms of paired bosons in section 2, we discuss the general g0→g quench and calculate the aftermath time-evolved wavefunction in section 3.We note specifically that the expression of the time-evolved wavefunction depends on the choice of Bogoliubov quasiparticles.The correspondence between the wavefunction overlaps, including the Loschmidt echo, and the largest entanglement eigenvalues, is examined in section 4.Numerical results on the fermionic lattice model are presented in section 5.The discussion and conclusion is given in section 6.

2.The paired bosonic Hamiltonian

As a description of a 1D Luttinger liquid,the Hamiltonian we consider here takes the following form [18]:

whereis the annihilation (creation) operator of a bosonic particle with momentum q.For Luttinger liquids,the dispersion relation and the pairing strength are given as [12]

The above Hamiltonian can be diagonalized via the Bogoliubov transformation:

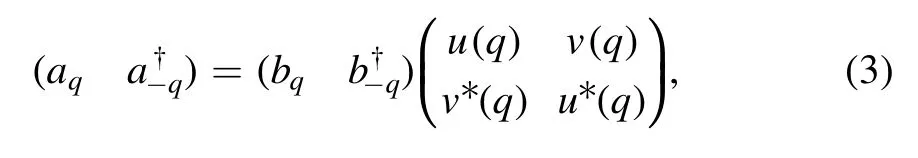
where the condition of∣u∣2− ∣v∣2= 1is imposed to preserve the bosonic commutations for the newly introduced aoperators.Since ω(q) and g(q) are real functions, u, v can be set to be real and parameterized by θ(q) as

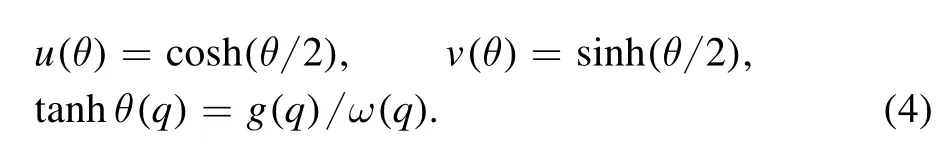
Under the above Bogoliubov transformation, equation(4),(the condition of∣g∣ <∣ω∣needs to be met in order to guarantee the existence of a solution), the pairing Hamiltonian,equation(1),can be transformed into a diagonal form in terms of the Bogoliubov operators aq:

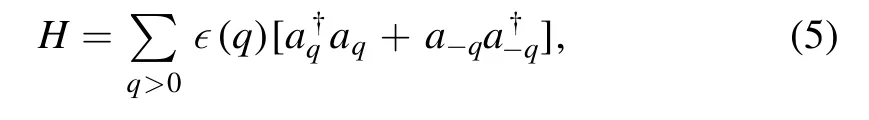
where∊(q) =We note that for ω(q) and g(q) given by equation (2), θ is actually q independent.For simplicity, in the new Hamiltonian in equation (5) the constant term −∑q>0ωqhas been dropped compared to the original Hamiltonian, equation (1).

The Bogoliubov Hamiltonian,equation(5)indicates that GS of the system should be the vacuum state of a-operators, i.e.aq|GS〉=0 is satisfied for each q.It is easy to verified that|GS〉can be expressed as a pairing state of the constituent particles as:

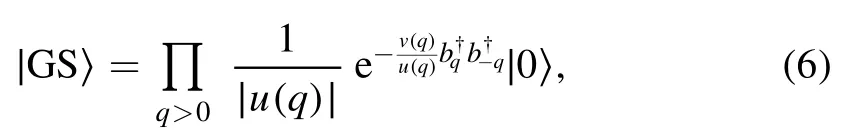
where 1/∣u(q)∣serves as the normalized factor.Throughout this paper,|0〉is reserved to specify the vacuum state of the original boperator, i.e.bq|0〉=0.

3.The g0 →g quench

The issue we are going to address is the quench dynamics on the pairing strength g: starting from an interacting (entanglement) GS with respect to some (nonzero) value g0, we switch the interaction strength abruptly from g0to another g value.What is the post-quench dynamics of the system?

For the Hamiltonian considered here, as mentioned before,the explicit form of the time-evolved wavefunction for the quench from the noninteracting limit(i.e.g=0)to a finite g has been obtained, together with a discussion of the correspondence between the Loschmidt echo and the entanglement in momentum space [18, 19].Here in this section by utilizing su(1, 1) Lie algebra, we make a further step by calculating the post-quench wavefunction for the general case of ∀g0→g (under the condition of∣g0∣and∣g∣ <∣ω∣).

The GS for the pairing strength g0, denoted as |GS0〉, is already given by equation (6).If we set the quench moment t=0, then

where λ0:=v0/u0, and the Bogoliubov coefficients u0, v0are determined by equation(4)for the given g0.Since(q,−q)-pairs with different q(q>0) in the Hamiltonian, equation(1), are indeed decoupled from each other, for notation simplicity we would like to drop the label of q in the formalism as long as there is no misunderstanding.The summation or multiplication over q(>0) can be restored easily if necessary.For instance,usu ally stands foras in the case of equation (7).

For the quench g0→g at t=0, the later-time wavefunction of the system is given by |Ψ(t)〉=U(t)|Ψ(0)〉, with the time-evolution operator U(t)=e−iH(g)t(ħ=1).Note that H(g)can be expressed in a diagonal form by its corresponding Bogoliubov quasiparticles (see equation (5)), and consequently,U(t) =exp [ − i∊t(a†a+.In this situation we have two sets of Bogoliubov quasiparticle operators, i.e.a0and a, corresponding to H(g0) and H(g), respectively.It can be shown that they are related by a composition of two successive Bogoliubov transformations (see equation (3)):

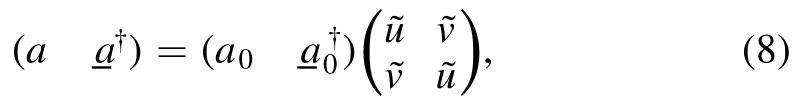
Equipped with the relation of a ↔a0from equation (8),we can write down an alternative form of U(t) in terms of a0operators:

where we have introduced K-operators as

and the coefficients in the exponents read

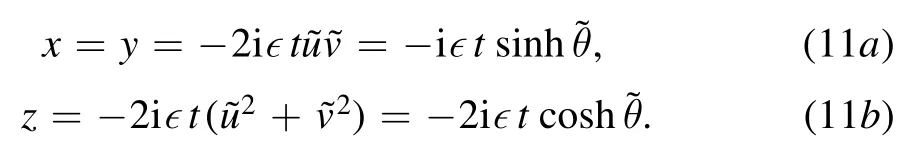
Note that the three Ks satisfy su(1, 1) algebra [20]:

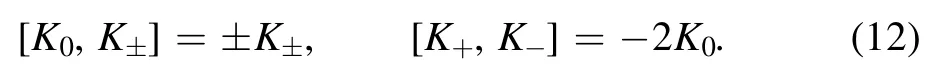
By employing the results of equation(A.3)in appendix A,the time-evolution operator U(t)in equation(9)can be factorized into a product form as

where particularly,

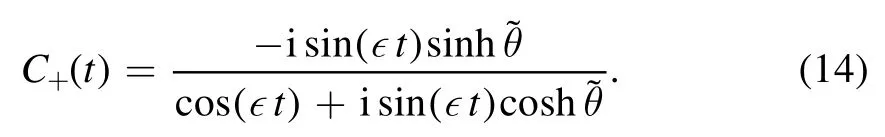
Then the normalized post-quench time-evolved wavefunction in terms of the a0-Bogoliubov quasiparticles can be written as

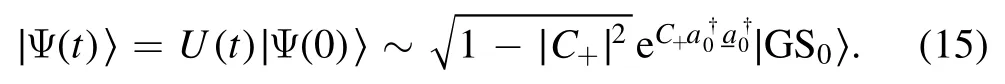
Here for simplicity we have dropped the phase factor owing to the action ofon|GS0〉,since it is not essential in our discussions.

If we are instead interested in the expression of |Ψ(t)〉 in terms of the original creation (annihilation) operator b†(b)with respect to its vacuum |0〉, we can employ the following procedure.First note that according to equation (B.8) in appendix B, the GS of H(g0) can be also expressed by an a0-pair generating operator acting on the vacuum |0〉:

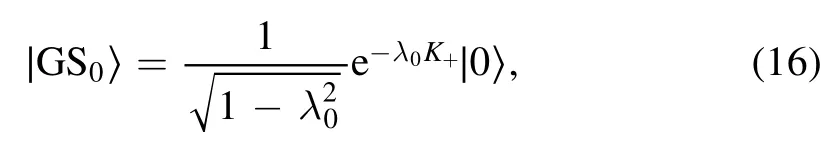
where K+is defined in equation (10).Combined with the result in equation (15), we have

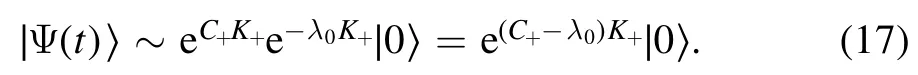
The next step is to express the exponential term ofin terms of b-operators, which is done in equation(B.6)in appendix B.By replacing τ →C+−λ0,and u →u0, v →v0there, we finally get

where we have put back the normalization factor explicitly,and

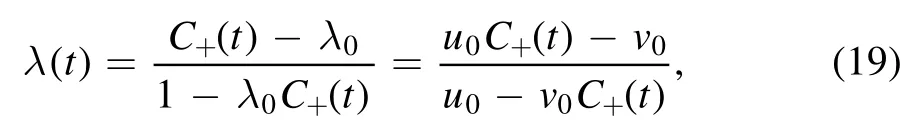
with λ0=v0/u0.

Up to now we have obtained two equivalent forms for the same post-quench wavefunction:one is written in terms of an a0-operator with respect to its vacuum |GS0〉 (see equation(15)),the other in terms of a b-operator with respect to the vacuum |0〉 (see equation (18)).

A few comments on C+(t)could be worth while.First we note that C+(t) in equation (14) can also be written as

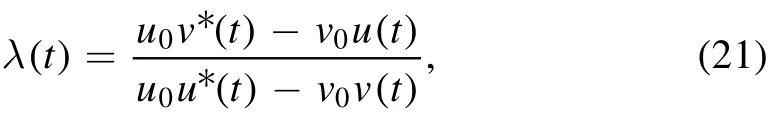
where u(t) and v(t) are given by equation (C.2).They appear as coefficients in the equation of motion for the b-operator(see appendix C), depending solely on the after-quench Hamiltonian H(g).For u0, v0, they are determined by g0via equation (4).

From the above analysis, we see that starting from a pairing state with the form of equation(7),when the system is subject to a g-quench, the aftermath time-evolved wavefunction still adapts a simple pairing form.Depending whether the a0-pairing or the b-pairing picture is chosen,the form of the wavefunction can be either equations (15) or (18).Indeed an observation can be simply made: for any given paired state that is the null state of a given class of Bogoliubov quasiparticle annihilation operators, it can be equally expressed as a paired state in terms of another class of Bogoliubov quasiparticle operators,with respect to their own corresponding vacuum state.Different classes of Bogoliubov operators are related via SU(1,1) (Bogoliubov) transformations as in equation (3).

4.Loschmidt echo and the entanglement in momentum space

One of the motivations of the present work for considering the general g0→g quench is to examine an interesting observation made by Dóra et al in [18], which has been mentioned in section 1.In that paper it has been shown that for the 0 →g quench about the Hamiltonian,equation(1),the largest entanglement eigenvalue in the momentum space is always identical to the Loschmidt echo.The observation has been confirmed on various lattice models to which the Luttinger liquid theory can be applied, including the prestigious XXZ model in its gapless phase [18].

Here for the general g0→g quench, the Loschmidt echo(or the return probability) can be defined as usual as the overlap of the initial GS wavefunction and the final state wavefunction [19, 21], i.e.

From the expression of |Ψ(t)〉 in equation (15), we have

since |Ψ(0)〉=|GS0〉.Or more precisely,L(t) = Πq>0(1 −∣C+(t;q)∣2)if the q dependence is restored.On the other hand, analogous to the discussion in[18], it is straightforward to show that the largest eigenvalue of the reduced density matrix ρA(t) for the right-movers of a0-Bogoliubov quasiparticles, denoted ashere, reads

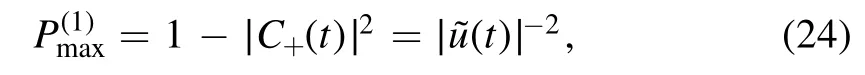
Thus similar to the 0 →g quench, the correspondence between the Loschmidt echo and the largest entanglement eigenvalue in the momentum space is established.

However when it comes to a numerical simulation on a lattice model, it is the Fock space of the constituent particles that we are going to work with, whose vacuum is the empty state of these particles by definition.It remains open whether the low-lying entanglement spectrum obtained in this Fock space after tracing out, say, the q<0 partition is identical to the one obtained from the effective Hamiltonian,equation(1).Indeed, from the results in the previous section, we note that the reduced density matrix ρA(t) and the subsequent entanglement spectrum can be evaluated by either the wavefunction in equation(15) or equation (18), where the vacuum is the null state of either a0operators or b operators.

We have addressed the situation with the wavefunction in equation(15) so far.For the other case, i.e.based on the wavefunction in equation(18), the entanglement between the left- and right-moving elemental excitations with respect to the b operators can be evaluated as before.The largest entanglement eigenvalue reads

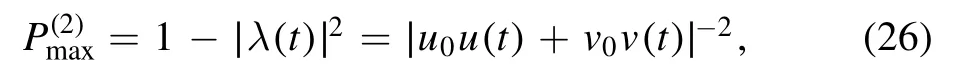
where the expressions of u(t) and v(t) (with respect to the g value) can be found in equation (C.2), and we note that here different fromin equation(25),

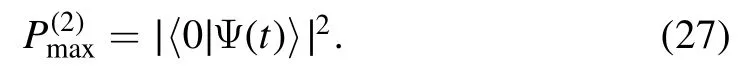
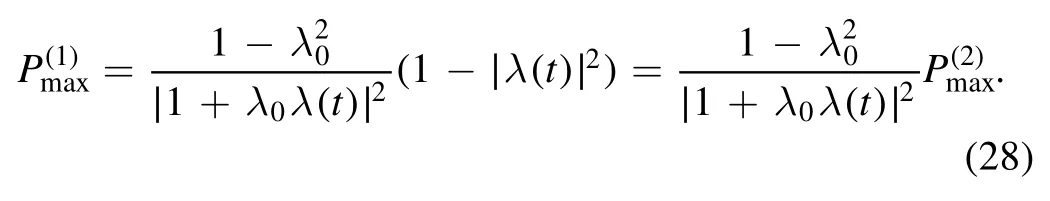
The above analysis shows that in the general g0→g quench, the correspondence between the Loschmidt echo defined in equation (22) and the entanglement eigenvalue holds, only when the entanglement of the left- and rightmoving elementary excitations is measured with respect to the initial GS of H(g0), i.e.|GS0〉.Here the excitations are nothing but the Bogoliubov a0-quasiparticles.It is worthwhile asking which entanglement is indeed being evaluated in the numerical simulations on lattice models, and consequently to what kind of wavefunction overlap the largest entanglement eigenvalue corresponds.We will address this issue in the next section by examining a spinless interacting fermionic lattice model,which is closely related to the prestigious XXZ model.

5.Numerical results

The Hamiltonian of the S=1/2 XXZ model,which describes the Heisenberg-type interaction between neighboring 1/2-spins along a chain, reads

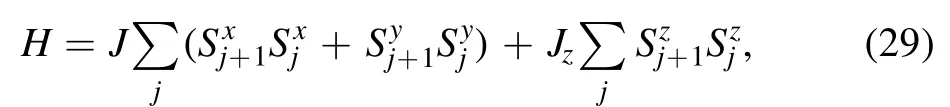
wheres are spin operators at site j.Employing the Jordan–Wigner transformation that maps the spin operators into a set of fermionic ones with extra nonlocal string terms, the spin Hamiltonian can be recast into a system of spinless interacting fermions:

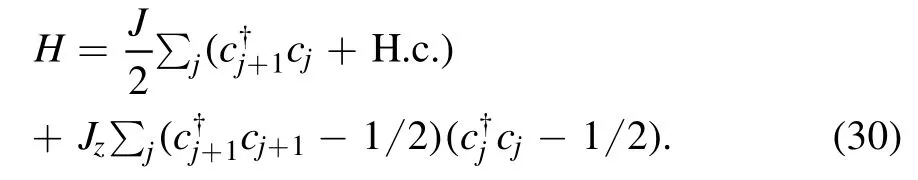
We see that the XX terms in the spin Hamiltonian are simply transformed into the hopping terms in the fermionic Hamiltonian.Meanwhile,the Jz-terms produce the scattering terms.

In the momentum space the Hamiltonian, equation(30)reads

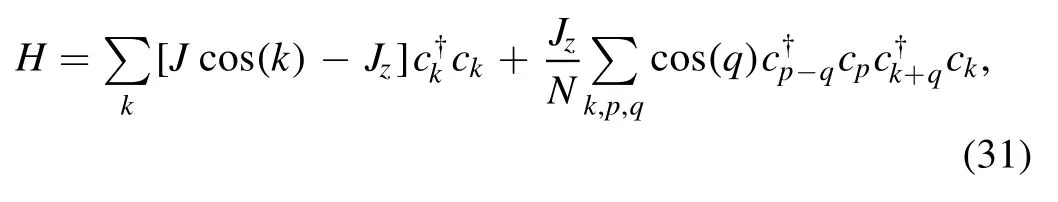
with a constant term JzN/4 (N is the lattice size) being dropped.We may define a parameter Δ:=Jz/J, which measures the strength of the uniaxial anisotropy along the z direction.In the following discussions, we set J=1.The energy and time are measured in units of J and J−1, respectively.It is well known that the XXZ model is critical (gapless) in the interval∣ Δ∣ ≤1, with a spin-singlet GS.Correspondingly,the GS of the Hamiltonian,equation(31),in this regime takes place at the half filling, and its low-energy physics can be well described by the Luttinger liquid,e.g.see[12, 22, 23].

The above result can be understood as a natural ramification of the HF↔HBcorrespondence.Let us first consider the equilibrium case and take a look at the simple noninteracting case.It means Δ(:=Jz/J)=0 in HF, or equivalently, g=0 in HB(K=1).In either situation, we have free particles with momenta as good quantum numbers.Both ground states are disentangled in momentum space,with only a single nonzero entanglement eigenvalue P=1.As the interaction is turned on,which means Δ ≠0 on the fermionic side, we can expect that the entanglement between the q>0 and q<0 partitions will develop due to the interaction,yet it may not be easy to write down the wavefunction explicitly to figure it out.On the other hand, compared to the rather complicated situation on the fermionic side, the momentumspace entanglement can be much more easily estimated from the GS wavefunction of the bosonic counterpart (see equation (6)),where the entanglement between (q, −q)-pairs with respect to the b-operators can be readily read out.

If we agree with the effectiveness of the Luttinger liquid description of HF[14, 15], we can expect that in the nonequilibrium case,the time evolution of the entanglement in the general Δ-quench over HFshould follow the features of its bosonic partner, as long as the Δ ↔g relation is sustained.Thus,the arbitrariness in the entanglement calculation for the g0→g quench in HBcan be removed:we need to stick to the b-representation consistently and adopt the time-evolved wavefunction in the form of equation (18), in order to make reasonable a comparative study with its fermionic counterpart.Specifically in this section, we have ratified the speculation on the relation between the time-dependent largest entanglement eigenvalue and the overlap of wavefunctions for general quenches,which is drawn from the analysis on the bosonic case(see equation(27)),for the interacting fermionic lattice model.

6.Discussion and conclusion

In this work,we first consider a paired bosonic model,which serves as an effective Hamiltonian for spinless Luttinger liquids.By employing su(1, 1) algebra, we derive the exact form of the time-evolved wavefunction under general interaction quenches on pairing strength.The method we employ and the results are general as long as the pairing takes place in the individual (q, −q) channels.The application to the fermionic case is straightforward,with only the su(1, 1)algebra being replaced by su(2) .

Based on the analytic form of the wavefunction, we reexamine under the general quench setup, the correspondence between the entanglement spectrum and the wavefunction overlap, including the Loschmidt echo.We note that by employing different sets of Bogoliubov quasiparticles, the expression for a given time-evolved post-quench quantum state can be different.It leads to an ambiguity in measuring the entanglement of paired bosons.However, by working numerically on an interacting spinless fermionic model that is closely related to the XXZ spin chain, we find that the ambiguity can be removed if the concurrence between the fermionic and bosonic descriptions is required.More specifically, we confirm that on the fermionic lattice model, the time-dependent largest entanglement eigenvalue in the momentum space coincides with the overlap between the time-evolved wavefunction and its noninteracting GS, rather than the initial state when the quench starts.

It is well known that quantum entanglement plays a key role in understanding the nature of the quantum world,especially of many-body systems [25, 26].The entanglement entropy and entanglement spectrum have been routinely investigated in the study.Up to the present most studies predominantly focus on real or orbital space entanglement.For many gapped systems, the congruity between the energy spectrum of the edge states and the entanglement spectrum obtained in this manner has been established [27–29].Nevertheless for critical(gapless)systems,due to the absence of an energy gap, the intrinsic entanglement might not be evidenced by cuttings in real space,which is corroborated by the observation of the slow decay of the eigenvalue spectrum of the reduced density matrix in the real-space density-matrix renormalization group (DMRG) [30].

Consequently, the issue of the entanglement structure in momentum space in gapless systems was raised and explored,first for spin chains [31–34], then for other correlated systems,including, for example, the Hubbard model [35] and the disordered fermionic systems [36, 37].In the framework of the Luttinger liquid theory, where the elementary excitations fall into left- and right-moving (weakly) interacting particles, it is particularly natural to consider partitioning the many-body Hilbert space by momentum.It is quite significant that the correspondence between the largest momentum-space entanglement eigenvalue and the wavefunction overlap in nonequilibrium dynamics, which is rather plain in the effective bosonic model,has been verified by the numerical observations on interacting lattice models.It suggests that the entanglement in momentum space can furnish a new perspective for the study of nonequilibrium dynamics of quantum critical many-body systems.

Furthermore,from the perspective of the development of numerical algorithms, the investigation on the momentumspace entanglement can help to improve the performance and identify the most fruit-bearing applications of the (timedependent) momentum-space DMRG [30, 38].For example,there have been reports on the persistence of the entanglement gap in momentum space beyond the physically critical points,and the saturation of the entanglement entropy in nonequilibrium dynamics[18,33,37].The DMRG working in the momentum space might have the potential to outperform its traditional real-space counterpart in these regimes.

Before concluding this section,we would like to mention that as far as the correspondence in quench dynamics is concerned,there may be some interesting issues remaining for investigation, which are beyond the scope of the present work.For instance, we notice in the numerical simulations that the correspondence we have discussed largely holds even beyond the regime of the gapless phase where the Luttinger liquid theory works well.To be precise, for the quenches crossing through the Berezinsky–Kosterlitz–Thouless (BKT)critical point(Δ=1),which separates the gapless phase from the Ising antiferromagnetic gapped phase,the correspondence sustains up to some critical value of Δ>1 (e.g.around Δ ∼1.6 for Δ0=0.5).In contrast, for the quenches moving in the opposite direction, i.e.from the critical phase to the gapped ferromagnetic phase across the first-order-like critical point (Δ=−1), the behaviors are quite different, and the agreement quickly dissolves.To study and understand the extent of the validity of the predictions from the Luttinger liquid theory will be interesting.

Acknowledgments

H.L.acknowledges support from the National Natural Science Foundation of China (Grant Nos.11474136, 11874187 and 12047501).

Appendix A.The Baker–Campbell–Hausdorffrelation

In this appendix, we show that the operator U(τ) with the form

can be expressed as

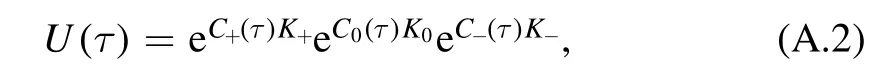
where K0and K±satisfy su(1, 1) Lie algebra (see equation (12)) [39], and x, y, and z are constants.The coefficients in the exponents in equation (A.2), which satisfy the initial condition of C+(0)=C−(0)=C0(0)=0, are given by

where r1,2are the roots of a quadratic equation of t:yt2+zt+x=0.Note that the solution, though quite general,is not applicable in all situations,e.g.it fails when r1=r2.We will discuss a specific example for this case in appendix B.

Following the procedure detailed in [20], the derivation of the above result is quite straightforward.First note that the operator U(τ) satisfies a differential equation as

Substituting the second form of U(τ)from equation(A.2)into the equation, and using the commutation relations of Ks, we can obtain the differential equations for C-coefficients as

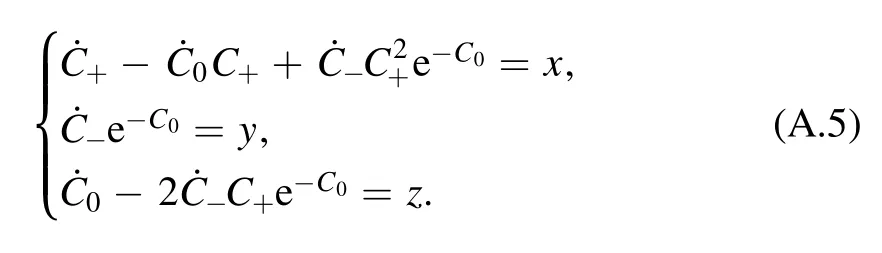
The above equations, although nonlinear, can be integrated analytically.For instance, the equation for C+can be written as

which can be solved by separation of variables:

Appendix B.The decomposition of expIn this section as a supplement to the discussion in appendix A, let us consider an exponential form of the pair creation operators of the Bogoliubov quasiparticles,U(τ) ≔ exp(τa†a†).Note thata†=ub†+vb(see equation(3),and we also confine ourselves to real u, v), we have

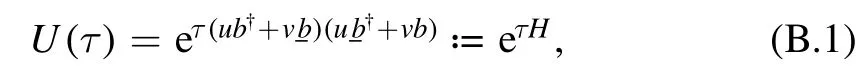
with

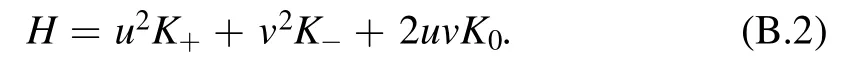
The K operators,as a realization of su(1,1)Lie algebra,are given by

Though we cannot apply directly the result in equation(A.3)since here r1=r2=−u/v,the coefficients inequation(A.2)can still be solved as follows.From equation (A.6), we have

Then

and

We obtain consequently

As an application of equation(B.6),let us consider the GS of the Hamiltonian, equation (1), which, in our simplified notation,reads

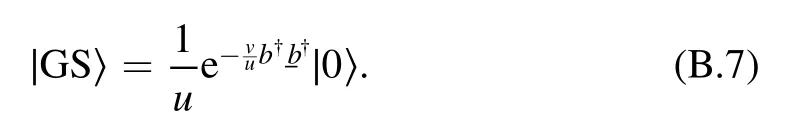
We say that the GS can also be expressed as

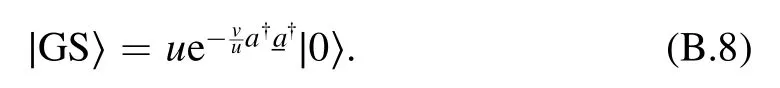
The conclusion can be verified in a straight way by means of replacing τ in equation (B.6) with −v/u, and using the fact that|0〉 is the vacuum state of b, i.e.b|0〉=0.

At the end of this section, an extra comment might be interesting.Note that equation (B.8) can be rewritten as

Here we see that there is some kind of duality between equations (B.7) and (B.9).For the vacuum of the constituent particles,i.e.|0〉,we can equally regard it as a kind of pairing state of Bogoliubov quasiparticles as well, with respect to its own vacuum state.

Appendix C.The equation of motion for b-operators

Consider the operator b in the Heisenberg picture b(t)=eiHtb e−iHt, with H given by equation (1).Then

where

In the above derivation, the Hamiltonian in another form of equation(5)and the Bogoliubov transformation, equation(3)(and equation (4)) have been used.

On the other hand, from the definition of b(t), we have

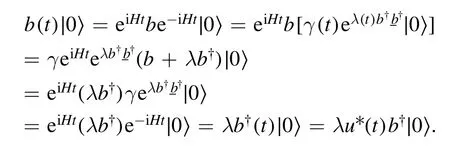
The comparison of these two equations produces

Actually by employing the same strategy with the same assumption about |Ψ(t)〉, we can show that for the general g0→g quench, the coefficient λ(t) in the exponent is

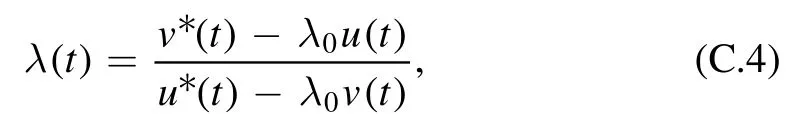
where λ0:=v0/u0, as for equation (7).It is identical to the result of equation(21) in the main text, which has been derived in a somewhat intricate but rigorous way by employing su(1, 1) algebra.

ORCID iDs