Uncertainty relation of successive measurements based on Wigner–Yanase skew information

Jun Zhang, Jia-Ning Wei, Zhou-Bo Duan, Kan He and Chang-Shui Yu

1 College of Data Science, Taiyuan University of Technology, Taiyuan 030024, China

2 College of Mathematics,Institute of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China

3 School of Physics, Dalian University of Technology, Dalian 116024, China

Abstract Wigner–Yanase skew information could quantify the quantum uncertainty of the observables that are not commuting with a conserved quantity.We present the uncertainty principle for two successive projective measurements in terms of Wigner–Yanase skew information based on a single quantum system.It could capture the incompatibility of the observables,i.e.the lower bound can be nontrivial for the observables that are incompatible with the state of the quantum system.Furthermore,the lower bound is also constrained by the quantum Fisher information.In addition,we find the complementarity relation between the uncertainties of the observable which operated on the quantum state and the other observable that performed on the post-measured quantum state and the uncertainties formed by the non-degenerate quantum observables performed on the quantum state, respectively.

Keywords: quantum uncertainty relation, successive measurements, Wigner–Yanase skew information

1.Introduction

The Heisenberg uncertainty principle is one of the well-known fundamental principles in quantum mechanics proposed by Heisenberg in 1927 [1].The result shows that anyone cannot specify the values of the non-commuting and canonically conjugated variables simultaneously [2].Acting as one of the fundamental properties of quantum mechanics, it could be wildly used in quantum information and processing, such as quantum key distribution [3–5], quantum cryptography [6–8], entanglement witness [9–14] and so on [15, 16].

With the help of different quantization methods of the observable’s uncertainty, the uncertainty relation can be divided into the following categories: 1) variance-based uncertainty relation,i.e.the uncertainty of the observable can be quantified by the variance, and it could construct two versions of the uncertainty relation, that is the sum of variances and the product of the variances; 2) entropic uncertainty relation, i.e.the uncertainty relation can be divided into several types based on different entropies, including smooth entropy[17],K-entropy[18],Rényi entropy[19–25],collision entropy [26, 27] and Tsallis entropy [28–35].

In 1963, Wigner and Yanase introduced skew information [36], and it could quantify the amount of information on the values of the self-adjoint operator X, which is not commuting with the density operator ρ, that is

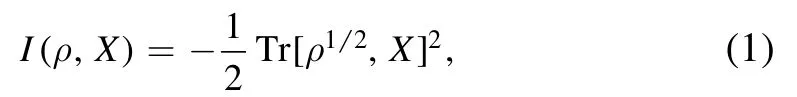
where[·,·]denotes the commutator.It could also be interpreted as a kind of quantum uncertainty X in the quantum state ρ.For a pure quantum state, the skew information I(ρ, X) will equal the variance ΔρX= TrρX2−(T rρX)2while, for the mixed quantum state,ΔρX ≥I(ρ,X)exists.Thus,if the initial quantum state is mixed, the variance ΔρX is a classical and quantum uncertainty hybrid.Luo divided the variance into two kinds,the classical and the quantum uncertainty,to embody the essence of the quantum mechanical[37].The reason for regarding Wigner–Yanase skew information as a kind of quantum uncertainty is that the skew information I(ρ,X)is convex concerning ρ,which is consistent with the intuitive idea that classical mixing cannot increase quantum uncertainty.The other reason is that when ρ and the observable X commute, skew information I(ρ, X) vanishes,which is consistent with the intuitive idea of reducing the classical regime when quantum objects commute.Thus, the Heisenberg uncertainty principle could be quantified in terms of the skew information by the following relation

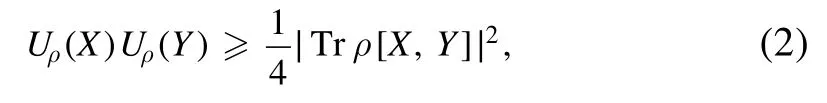
where the quantum uncertainty Uρ(X) can be quantified byHowever, almost all of these uncertainty relations will suffer from the trivial result if the observables X and Y are incompatible with the quantum system’s state.Just like the excellent work deal with the problem of the lower bound,it could arrive at a trivial bound if the quantum state ρ leads to the zero expectation value of the commutator.

Subsequently, researchers give all kinds of uncertainty relations based on the Wigner–Yanase–Dyson skew information

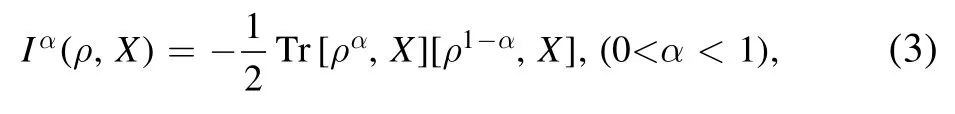
and two kinds of generalized Wigner–Yanase–Dyson skew information, where one is [38]

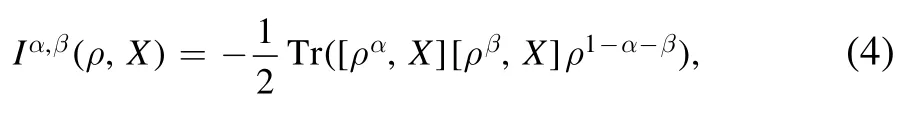
where the coefficients α and β satisfy α,β>0,α+β<1.The another one is [39]

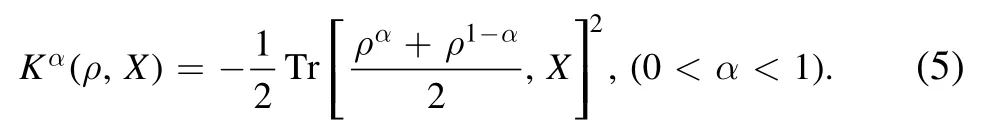
It is worth noting that they can constitute various uncertainty relations[40–49].They shed new light on our understanding of uncertainty.In addition, most of these aforementioned research studies mainly focus on the measurements of two observables or multiple measurements,which are separately performed on two or multiple identical quantum states that are taken into account.In fact, the uncertainty relation essentially expresses the limitations imposed by quantum theory on the preparation of ensembles of systems in identical states,which has been clearly explained in the conceptual foundations of quantum theory by Home[50].However,it is impossible to prepare an ensemble of identical particles.To explore the influence of the measurement of one observable on the uncertainties in the outcomes of another, we have to formulate an uncertainty relation for successive measurements: namely, what if the two measurements are successively performed on a quantum state?

In this paper,we investigate the uncertainty relations related to such successive projective measurements: namely, the measurement of the second observable is performed on the quantum state generated after the measurement of the first observable with all the information erased.Our results show that the quantum Fisher information can construct the lower bounds of the uncertainty relation.The lower bound can be nontrivial for the observables that are incompatible with the state of the quantum system.It could capture the incompatibility of the observables, i.e.the lower bound can be nontrivial for the observables which are incompatible in the state of the quantum system.In addition,we find the complementarity relation of two kinds of uncertainties of the observables.

The paper is organized as follows.In section 2, we briefly review the concepts of Wigner–Yanase skew information and its properties.Section 3 provides the uncertainty relation for successive projective measurements based on Wigner–Yanase skew information.In section 4,we take the successive measurements of two observables as an example.Finally,we draw the conclusion.

2.The concepts of skew information and the properties

Let us give a brief introduction to Wigner–Yanase skew information.In 1963, Wigner and Yanase introduced skew information [36], and it could quantify the amount of information on the values of the self-adjoint operator X, which is not commuting with the density operator ρ, that is

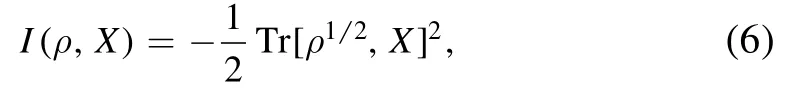
where [·, ·] denotes the commutator.

It has so many nice properties, such as

Due to the fact that Wigner–Yanase skew information has good basic properties, it can be applied to construct quantum uncertainty, quantify the quantum correlation, measure the quantum coherence, and so on.

3.Uncertainty relation of successive measurements based on Wigner–Yanase skew information

Theorem 1.For a pair of non-commutative observables A and B, there is the uncertainty relation of successive measurements based on Wigner–Yanase skew information

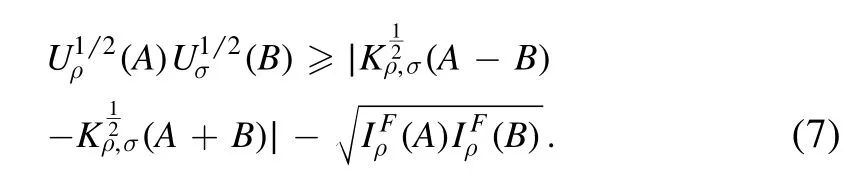
In particular, σ denotes the final state generated by measurement A with all the information about the measurement outcomes erased.

Proof.Based on the definition of the generalized Wigner–Yanase–Dyson skew information

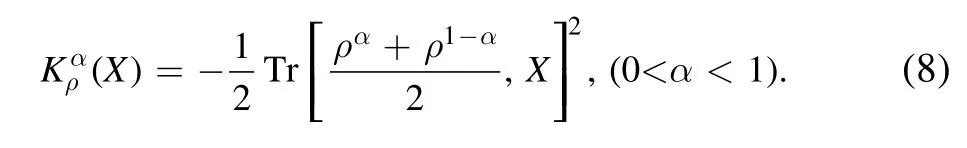
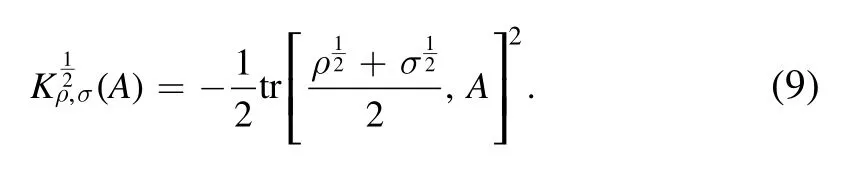
Thus, for a pair of non-commutative observables A and B,there is

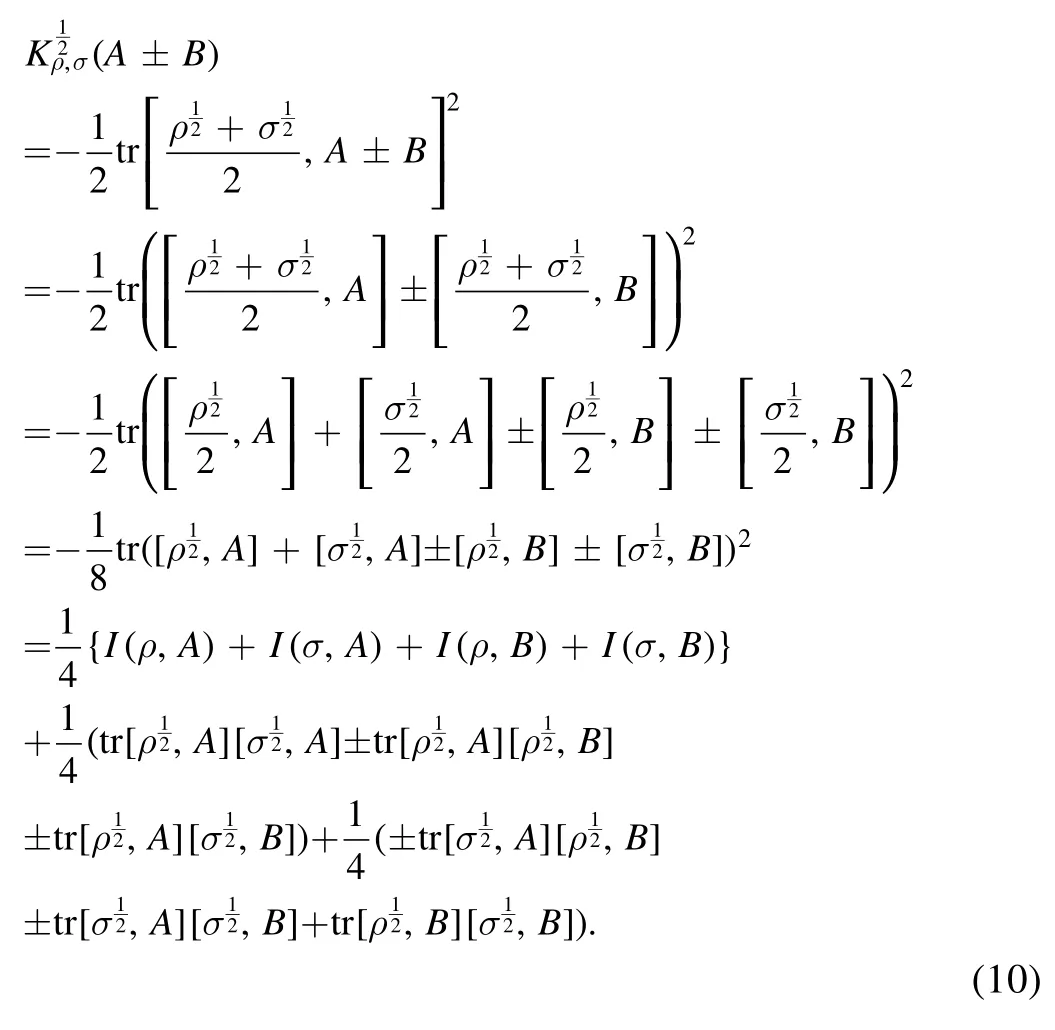
As we know, the post-measured quantum state σ will be commute with the observable A, i.e.= 0.Thus,the above equality and the Cauchy–Schwarz inequality implies

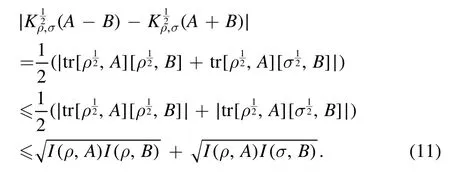
The first inequality comes from the Cauchy–Schwarz inequality, and the second inequality comes from the inequalityBy rearranging the inequality, it arrives at

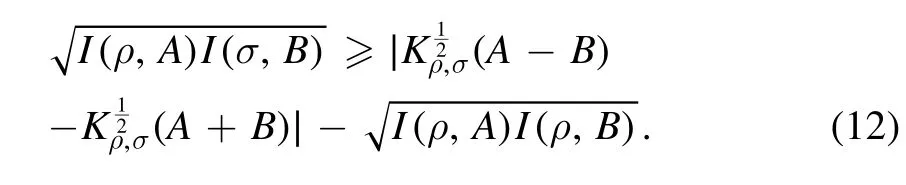
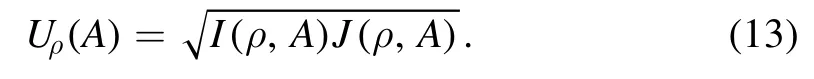
The uncertainty of the successive measurements can be defined

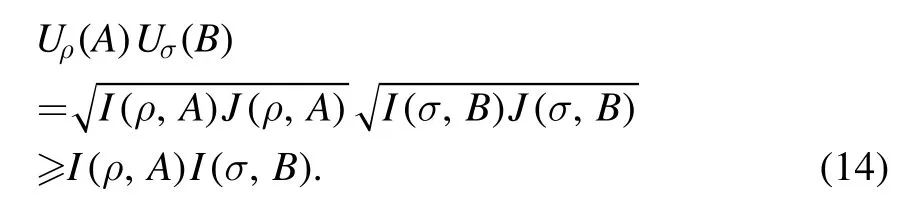
The inequality is fromI(ρ,A) ≤J(ρ,A).By combining equations (14) and (12), it will have

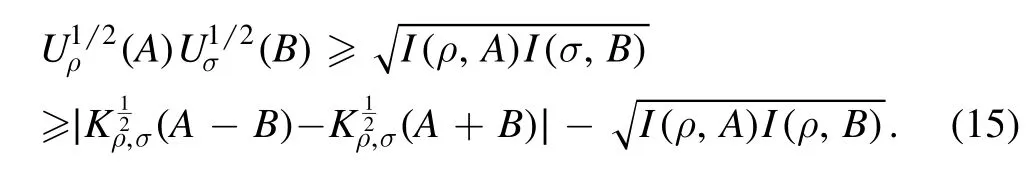
From the quantum metrology, quantum Fisher information and Wigner–Yanase skew information have the following relation [51]

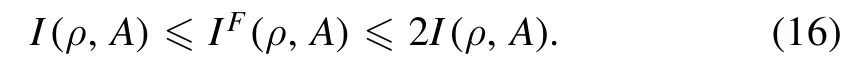
Thus, the uncertainty relation of successive measurements A and B will be bounded by the quantum Fisher information,equation (7).The proof is finished.□

It is evident that for the non-degenerate quantum obser-

Corollary 1.For a pair of non-commutative observables A and B, there is the complementarity relation between two kinds of uncertaintiesand

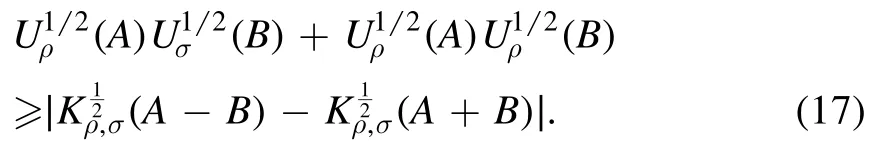
Proof.During the process of proof theorem 1, it has

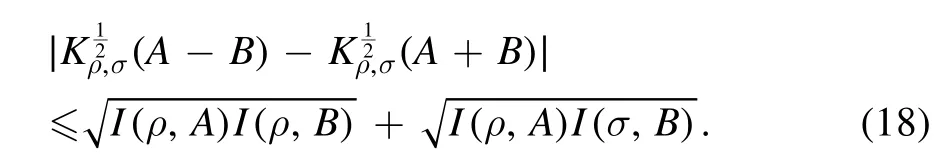
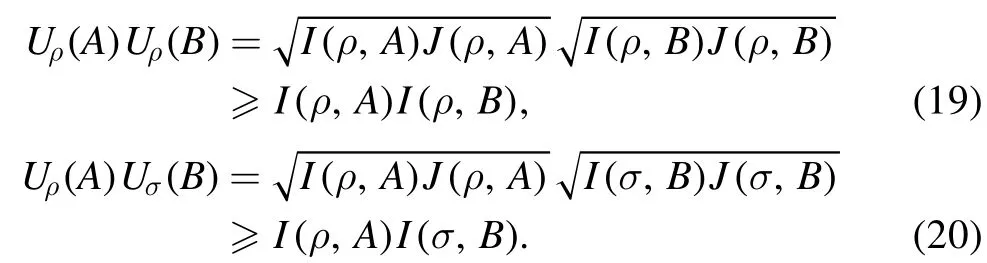
By substituting equations (19) and (20) into equation (18), it will arrive at equation (17).The proof is completed.□

4.Example

As an example,we intuitively present the uncertainty relation of successive measurements based on Wigner–Yanase skew information.The initial measured quantum state is a single qubit, which is given by

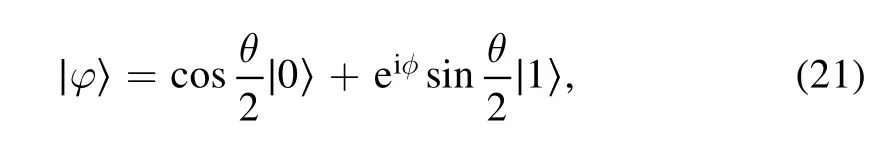
with θ ∊[0, 2π], φ ∊[0, π].

Take the observables A and B as σzand σx, respectively.Firstly,the observable A performs on the initial quantum state ρ=|φ〉〈φ|, and the post-measured state with all the information of the measurement outcomes erased is given byThen, the second observable B performs on the post-measured state σ.Thus,the uncertainties of the observables A and B can be quantified by

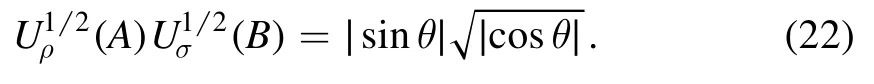
The bound of the uncertainty relation is given by

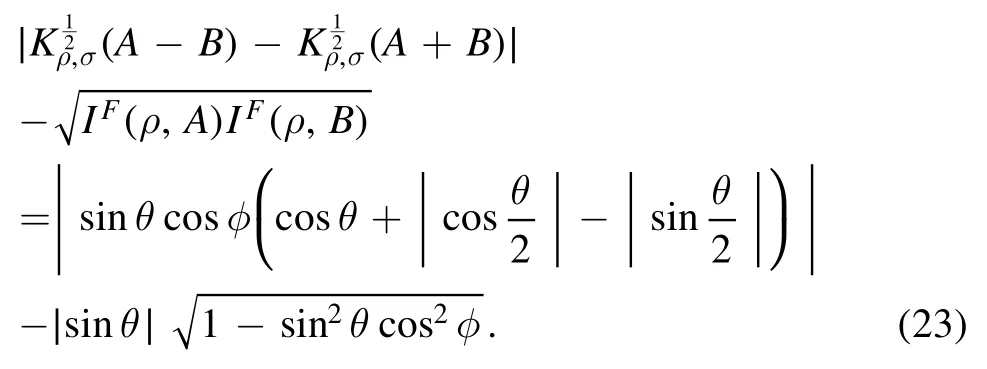
Figure 1 presents the difference between the left-hand and right-hand in theorem 1 versus the increasing parameters θ and φ.It is evident that the difference between equations(22)and(23)is always positive with the increasing parameters θ and φ.It illustrates that,for any single qubit,the influence of the measurement of one observable A on the uncertainties in the outcomes of another B will be effective bounds by equation (23).

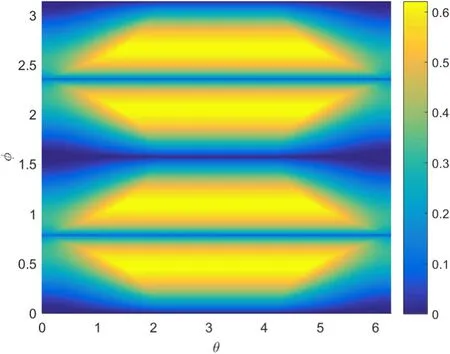
Figure 1.The difference between the left-hand and right-hand of the uncertainty relations in theorem 1 versus the parameters θ and φ of the initial quantum state.

Next, we consider the complementarity relation between two kinds of uncertainties,which describes the uncertainties of the observable A that operated on the quantum state ρ and the uncertainties of the observable B that performed on the post-measured quantum state σ, andthat describes the quantum observables A and B performed on the preparation of ensembles of systems in identical states ρ, respectively,

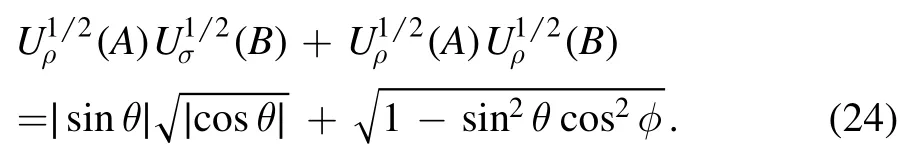
The bound of the complementarity relation is given by

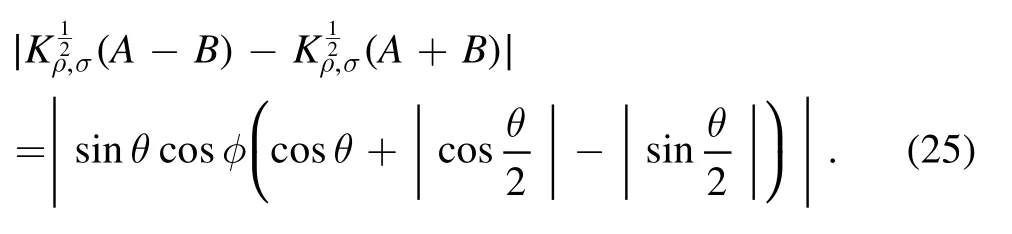
In figure 2, the difference between the left-hand and right-hand in corollary 1 with the increase in parameters θ and φ is evident.It is evident that the difference between equations(24)and(25)is always positive with the increasing parameters θ and φ.It illustrates that, for any single qubit,these two kinds of uncertainty relation satisfy the complementarity relations in corollary 1.

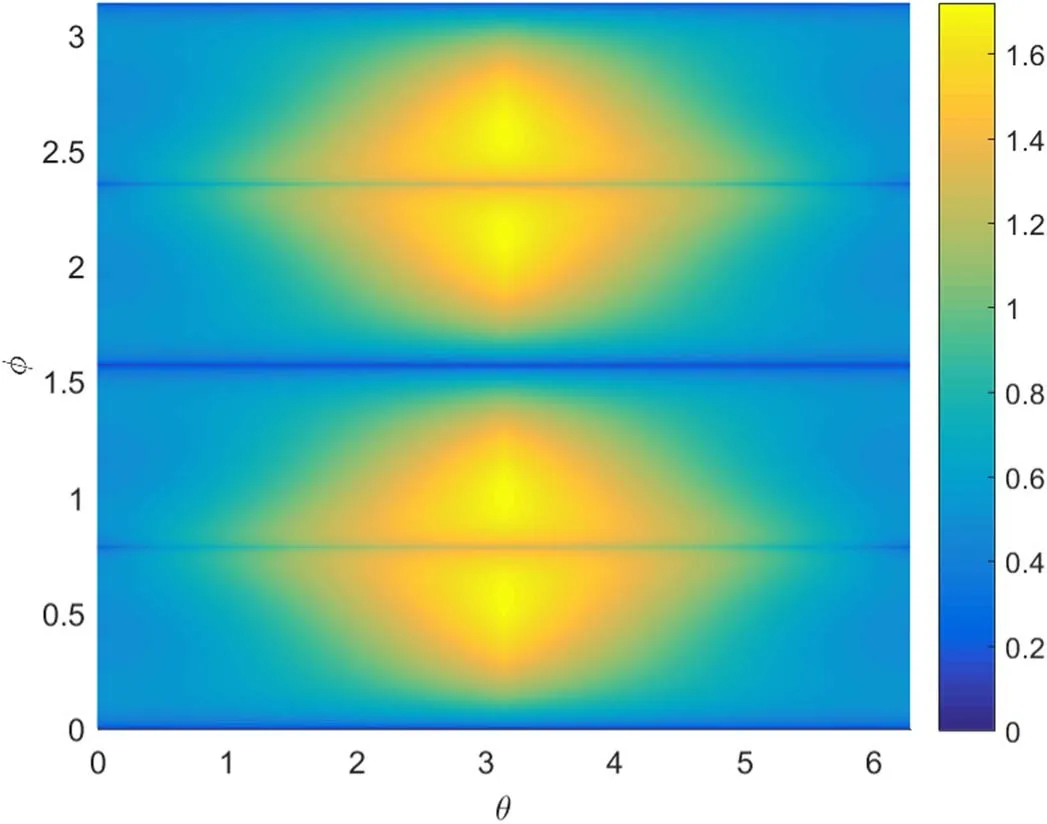
Figure 2.The difference between the left-hand and right-hand of the complementarity relations in corollary 1 versus the parameters θ and φ of the initial quantum state.

5.Discussion and conclusion

Due to the fact that Wigner–Yanase skew information could quantify the quantum uncertainty of the observables that are not commuting with a conserved quantity,we have proposed the Wigner–Yanase skew uncertainty principle for successive non-degenerate measurements based on a single quantum system that is based on the good basic properties of Wigner–Yanase skew information.The results show that the lower bound can be nontrivial for the observable, which is incompatible with the state of the quantum system.It is also constrained by the quantum Fisher information.During processing, we also find the complementarity relation between the uncertainties of the observable that operated on the quantum state and the other observable that performed on the post-measured quantum state and the uncertainties formed by the non-degenerate quantum observables performed on the quantum state,respectively.Finally,examples of the qubit system measured by two successive nondegenerate measurements demonstrate the validity of the uncertainty relations.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos.11771011, 11775040,12011530014), the Natural Science Foundation of Shanxi Province,China(Grant Nos.201801D221032,201801D121016)and Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (Grant No.2019L0178).