Local stability analysis of a low-dissipation cyclic refrigerator*
2022-02-18KaiLiJieLinandJianHuiWang
Kai Li, Jie Lin and Jian-Hui Wang,2
1 Department of Physics, Nanchang University, Nanchang 330031, China
2 State Key Laboratory of Surface Physics and Department of Physics,Fudan University,Shanghai 200433,China
Abstract We study the local stability near the maximum figure of merit for the low-dissipation cyclic refrigerator,where the irreversible dissipation occurs not only in the thermal contacts but also the adiabatic strokes.We find that the bounds of the coefficient of performance at a maximum figure of merit or maximum cooling rate in the presence of internal dissipation are identical to those in the corresponding absence of internal dissipation.Using two different scenarios, we prove the existence of a single stable steady state for the refrigerator, and clarify the role of internal dissipation on the stability of the thermodynamic steady state,showing that the speed of system evolution to the steady state decreases due to internal dissipation.
Keywords: local stability, system dynamics, low dissipation, cyclic refrigerator
1.Introduction
The optimal analysis on finite-time performance of thermal machines that include heat engines and refrigerators has attracted much interest [1–24], beginning with the seminar work[1].Among these,the low-dissipation model[12–25]in which the thermal-contact process is not quasi-static but close to the reversible limit was usually adopted, with the advantage that neither phenomenological heat-transfer laws nor quantum master equations are used.Under the low-dissipation assumption, the irreversible entropy production along a thermal-contact process is inversely proportional to the longtime duration t.Such a 1/t −scaling entropy production was theoretically proved in classical [26, 27] and quantum systems[28,29],and it was also validated in recent experiments[30,31]based on different platforms.A quite interesting topic is making a comparison between the low-dissipation model and the irreversible machines based on assumptions on the heat fluxes and considerations on the degree of irreversibility,as well as some specific models for quantum systems,showing that there is equivalence between them within certain optimal operation regime [24, 32].
When the machine proceeds in finite time, the irreversibility occurs not only along a thermal-contact process but also during a thermodynamic adiabatic process[3,15,33–36].The irreversible phenomenon in the latter case is usually associated with the internal friction that accounts for the irreversible entropy production.Such friction occurring in classical[3] or quantum [34, 35] systems is related to energy dissipation owing to the timescale disparity between internal dynamics and finite-time evolution [35].The irreversible entropy generation induced by the internal dissipation was recently proved to satisfy the 1/t2−scaling form along the nonadiabatic process with time duration t[37,38],though its exact evaluation depends on the system under consideration[34,35].The influence of the internal dissipation on the finitetime performance was intensively investigated for heat engines or refrigerators ranging from macroscale [15] to microscale [36–38].
While for a heat engine the optimization objective was usually power output and Omega function, for refrigerators a series of optimization criteria[15,17]were proposed,such as per-unit-time coefficient of performance ε/tcyc, Ω optimization criterion, and figure of merit χ=εQc/tcyc, where tcycis the total cycle period and ε=−Qc/(Qh+Qc),with Qc(Qh)being the heat absorbed from the cold (hot) reservoir.The analysis of dynamical behavior provides a suitable way to understand the stability near the steady state which, for heat engines, corresponds to maximum power or maximum Omega function [39–42].Since in low-dissipation models a general time-dependent formulation on irreversible entropy production are given,the stability dynamics around the stable point were proposed by analyzing the time evolution[39–42]instead of particularities in the heat exchange mechanism[43–45].Until now,a unified description of local stability for an irreversible refrigerator, where the internal dissipation exists due to a finite-time operation, is still unavailable.
In the present paper, we study the stability properties of a finite-time refrigerator where irreversibility occurs not only from thermal contacts but also from thermodynamic adiabatic strokes.The coefficient of performance is determined by optimizing χ figure of merit and the cooling rate with respect to the time durations along the four processes.The analytical expression for the optimal coefficient of performance is obtained,showing that the internal dissipation has no influence on the upper and lower bounds of the optimal coefficient of performance under maximum cooling rate or maximum figure of merit.We clarify the role that the dissipation plays along the four strokes in the stability of the refrigerator under maximal χ figure of merit.Finally, we study the relation between internal dissipation and system relaxation speed as well as the cycle period.
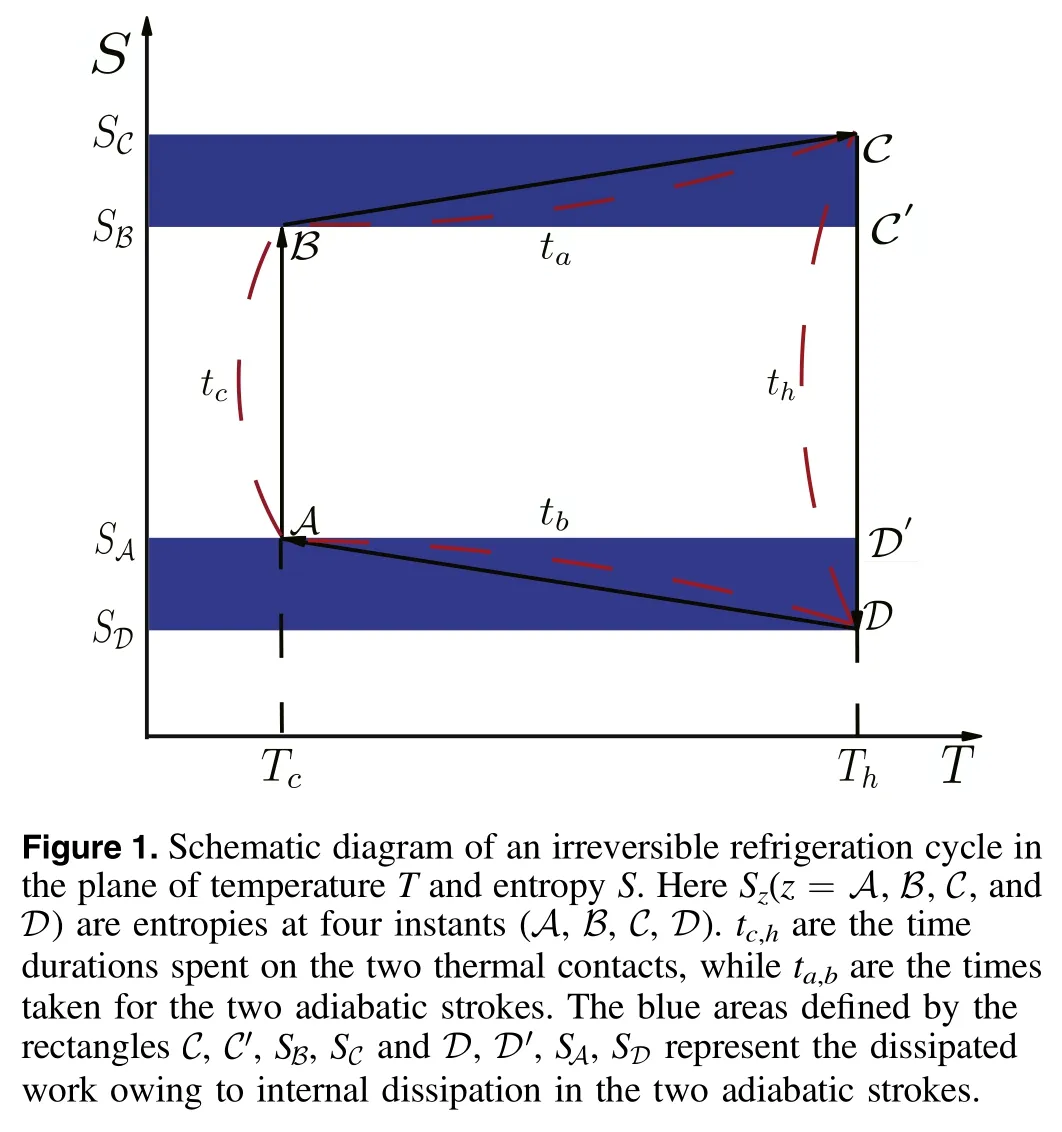
2.Model
We consider a refrigeration cycle consisting of two heat transfer processes (A→BandC→D) and two thermodynamic adiabatic branches (B→CandD→A), as sketched in figure 1, where the time durations of the four processes are indicated by tc,ta,th,and tb,respectively.While in the cooling or heating stroke the working substance is in contact with a cold and a hot heat bath of constant temperatures Tcand Th,respectively, during an adiabatic branch the working substance is isolated from either the hot or cold reservoir.In the branch B→C (D→A) work should be done to overcome the inner friction which results in heat, causing the entropy to increase fromSB(=SC′) toSC[SDtoSA(=SD′)], irrespective of the system is expanded or compressed.The entropy variations along the cold and hot thermal contacts can be expressed as ΔSc=SB−SA, and ΔSh=SD−SC, respectively.Notably,ΔSc←ΔShin the presence of internal friction, and ΔSc=−ΔShwhen friction is absent.For the engine model under consideration, the time durations ti(i=a, b, c, h) along these four irreversible processes are finite and therefore the total cycle period tcyc=ta+tb+tc+thshould be finite.
Let Qc(Qh)be a certain amount of heat along the cooling(heating) stroke; the variation of entropy can be given by

or
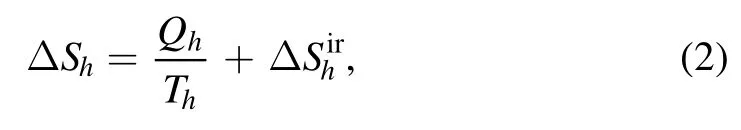


where ΔS ≡ΔSchas been used.When the internal dissipation occurs along the adiabatic process due to finite-time duration,the entropy change ΔShduring the heating process is dependent on the protocols of the two adiabatic strokes.This is quite different from entropy variation ΔSc=ΔS that is determined only by the initial and final states of the cooling stroke and taken as a state variable.


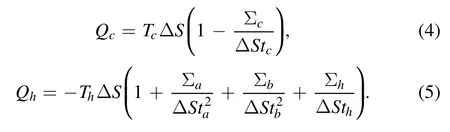
For each cycle, the total irreversible entropy production exclusively comes from the two heat reservoirs, namely, σ=−(Qh/Th+Qc/Tc), leading to
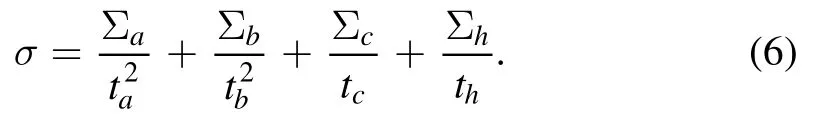
With consideration of equations (1) and (2), the main performance parameters,which includes the cooling rate(R=Qc/t),the coefficient of performance [ε=−Qc/(Qh+Qc)], and the figure of merit (χ=εR), can be obtained:

The coefficient of performance reaches the Carnot value,εC=Tc/(Th−Tc),but the cooling rate R vanishes,if and only if the cycle period tcycis infinitely long and the cycle is reversible.
3.Coefficient of performance under maximum cooling power and maximum figure of merit
We define the following dimensionless or scaled variables,which are
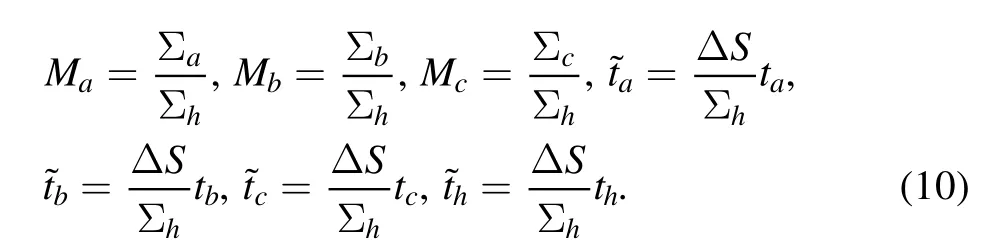
With these, the dimensionless heatsandexchanged along the two thermal contacts can be obtained from equations (4) and (5),

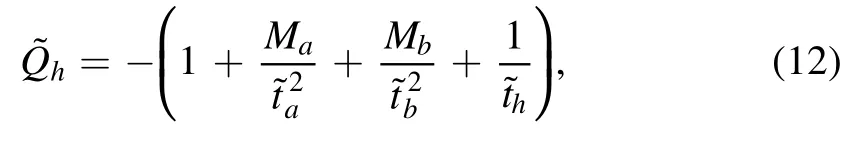
with τ=Tc/Th.It follows that, the normalized forms of equations (7), (8), and (9) are

respectively,withThe dimensionless form of the total entropy production (6) becomes

To reveal the machine performance under maximal cooling rate, we maximizeby setting= 0, leading to
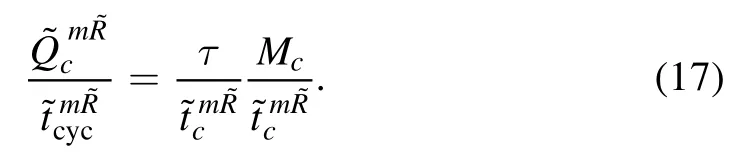
This, together with equation (16), gives rise to

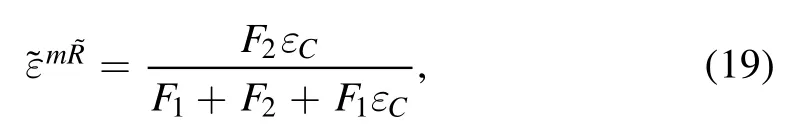


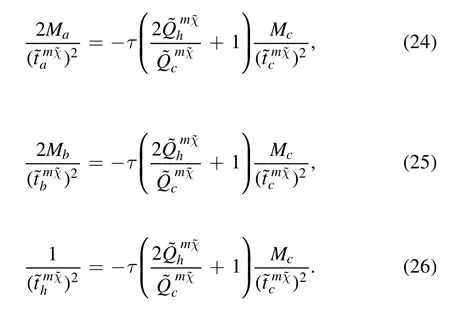
From equations (24), (25) and (26), we find that the time durations of the four thermodynamic processes are optimally distributed as
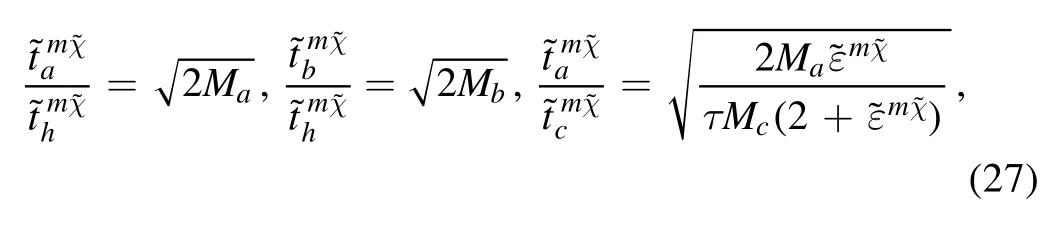
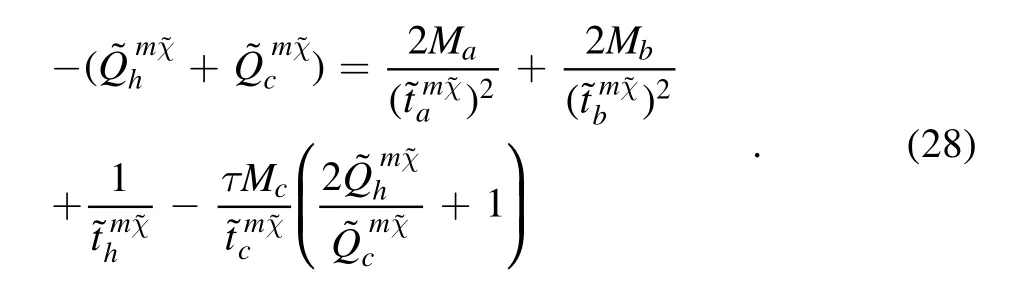
With consideration of equations (16) and (28), we have


4.Stability analysis based on the heat amounts exchanged per cycle
Since the mechanism of heat exchange is not explicitly presented in the irreversible machine,the dynamical evolution of the system will be addressed via associating heat exchanged or dissipated to time durations that are dynamical variables.When working under maximal figure of merit,the refrigerator for given control variables remains in the steady state under which these time durations reach a stable point.To proceed,the scaled time durations(i=a,b,h,c)can be re-expressed in terms of the fraction of the total cycle period



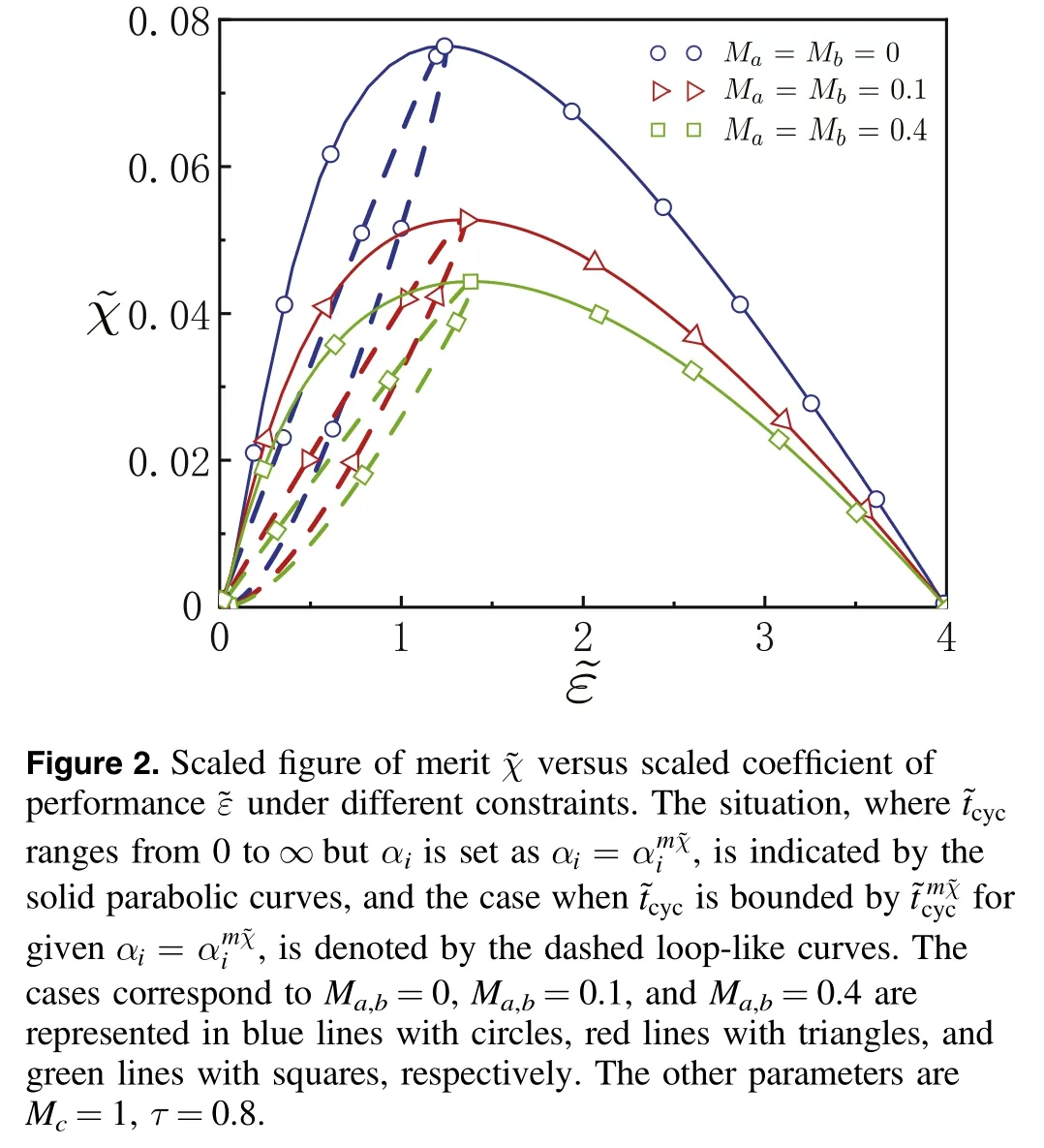


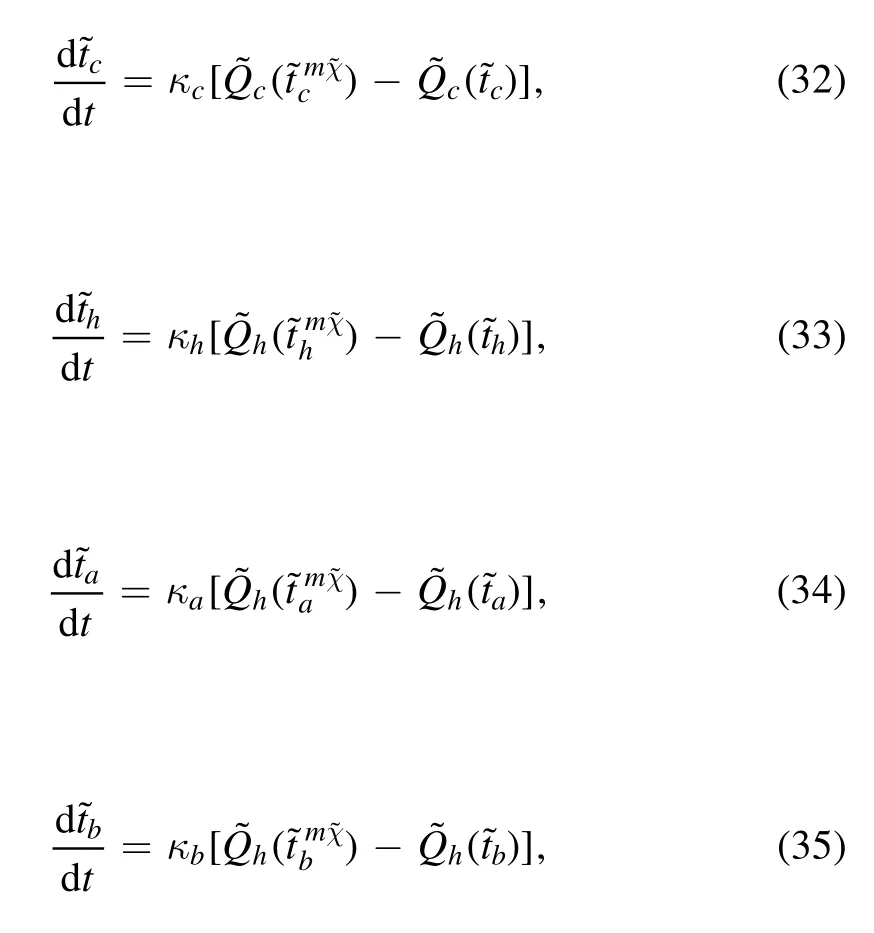




Beyond the linear approximation, the system dynamics can be analyzed by numerically solving equations (32), (33),(34), and(35).The velocity vector field of the system can be seen in the three-dimensional stream and the three-dimensional quiver plot on the phase space in figures 3(a) and (b),showing that a stable point exists and its location depends on the internal dissipation coefficient.

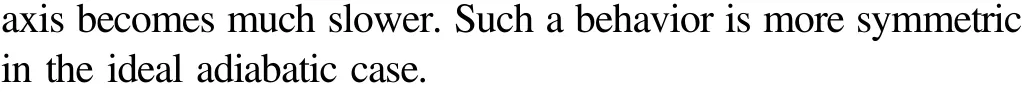
5.Stability analysis based on the cooling rate and figure of merit
We are now in a position to study the machine performance by optimizing figure of merit χ with respect to the total cycle period and time duration of cold thermal contact.To this end,we introduce the following set of dimensionless variables:
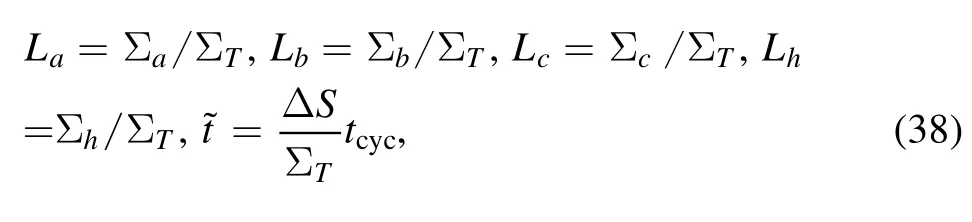
where ΣT=Σa+Σb+Σc+Σhand tcyc=ta+tb+tc+th.In terms of these variables, the dimensionless heat fluxes,are given by
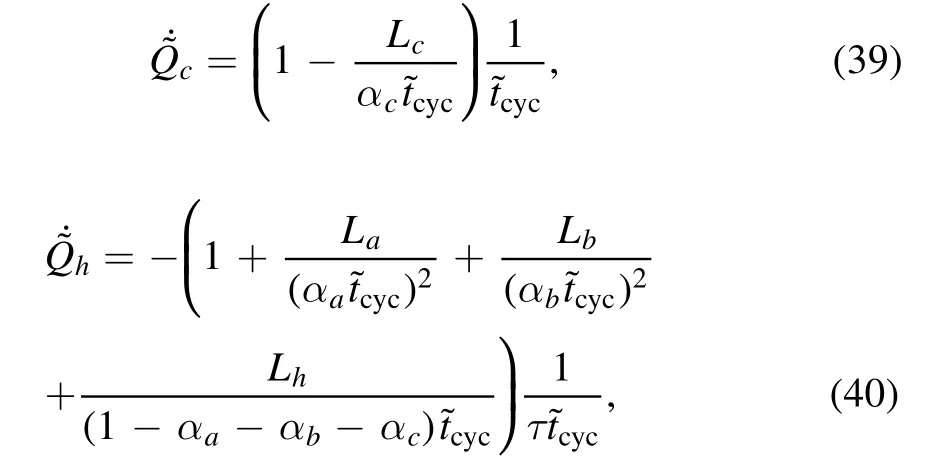
leading to

It follows that the optimal values of the variables under maximaldenoted byandcan be determined via numerical computation.Following the approach used in the previous section, we have

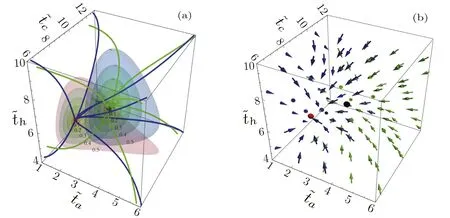
Figure 3.System dynamics determined by equations (32), (33) and (34).Streamline (a) and vector field (b) in planeare plotted.Three-dimensional surfaces of constant velocities in (a) show how fast the velocity changes as the system relaxes toward the steady state.Green and blue lines(arrows)correspond to the cases Ma=Mb=0.4 and Ma=Mb=0.1,respectively.The other parameters are κa,b,c=20,κh=10, Mc = 1, and τ=0.8.
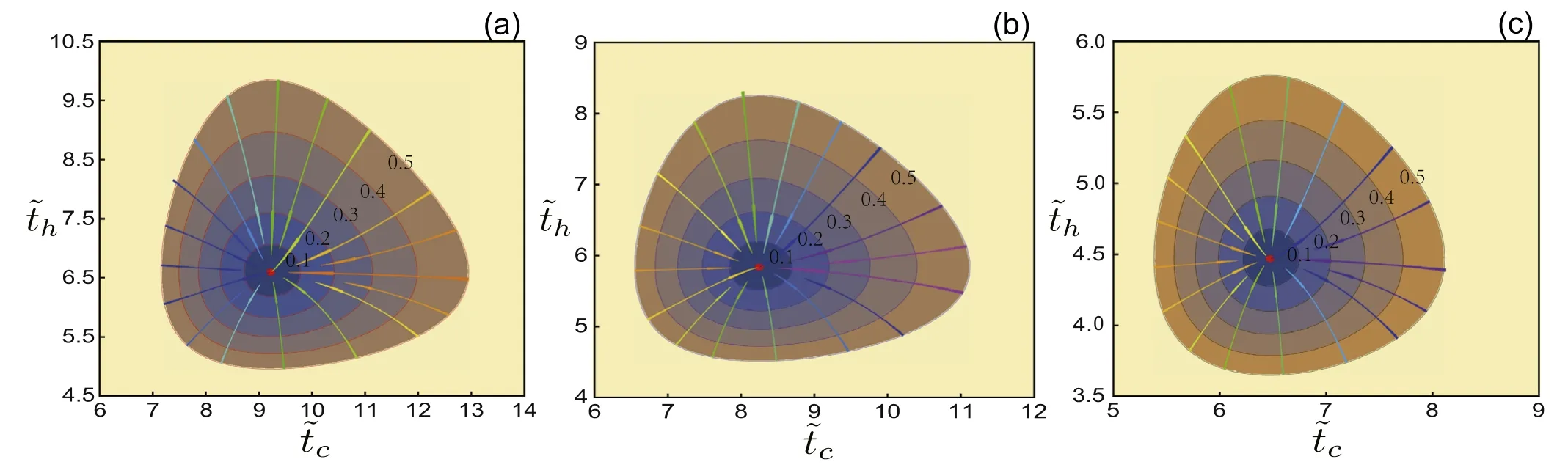
Figure 4.Representative stream plot of the velocity field for (a) Ma,b=0.4, (b) Ma,b=0.1, and (c) Ma,b=0.Dynamical velocity contour indicates the relaxation speed toward the steady states.Level curves of constant velocities show patterns over time and how fast the velocity changes as the system evolves to the steady state.The other parameters are the same as in figure 3.
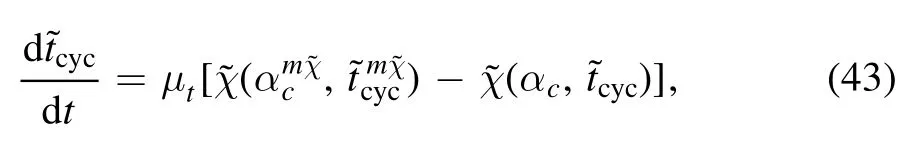
where μc,tare constant.The local stability of the corresponding steady state is determined according to

which becomes after performing the algebra:



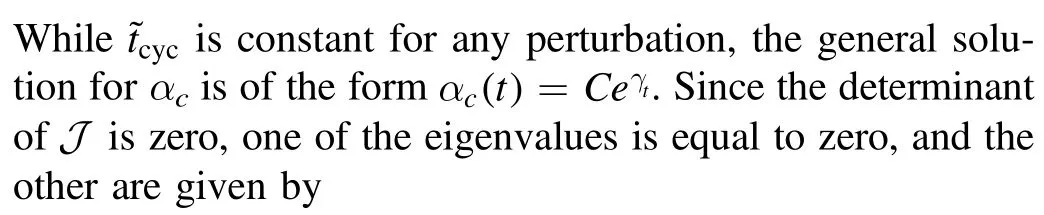
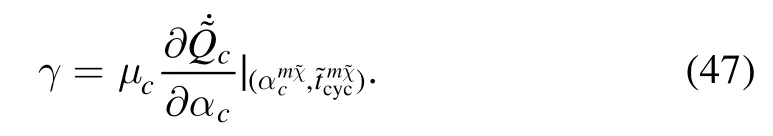
A relaxation time can be defined by the largest one of the valuesSince the relaxation time must be smaller than the total cycle time, the possible values of μ should satisfy the constraint:
We are in a position to explore the dynamic behavior of the system under different initial conditions.As an example,we consider the case when the internal dissipation is vanishing.In figure 5 we plot the dynamic behavior linked to the stability near the maximum figure of merit.For given values of μtand μc, in the first row the line integral convolution is plotted(a)without and(b)with internal dissipation,and in the second row the trajectories in phase space are presented (c)without and (d) with internal dissipation.From figure 5 we observe that, due to internal dissipation, the total cycle time for the machine is increased and the speed of returning to a steady state slows down.The streamlines will pass through the stable point ifWhenthese streamlines would not be able to spontaneously return to its original operation time, and the machine would stop cycling in this case.The second low in figure 5 shows that the trajectories indicating that the system can reach the steady state are bounded by the irreversible limit (red line) whenPhysically, fixing the total cycle time would limit the control for the refrigerator and affect the system irreversibility.When imposing constraints over the dynamics of the system, we should make a comparison between the relaxation time and total cycle time in order for the cyclic device to be stable under maximum figure of meritχ˜.

6.Conclusions
We have investigated the finite-time performance and the local stability for a cyclic refrigerator where the irreversible dissipation originates from both two thermal-contact and two adiabatic strokes.While the irreversible entropy production along the thermal contact satisfies 1/t-scaling form, the entropy generation during the adiabatic stroke follows the 1/t2−scaling behavior.Under the maximum cooling rate or figure of merit, we recovered the upper and lower bounds of the optimal coefficient obtained in previous models which were, however, limited to the frictionless case.


Throughout the paper we assumed the dissipation along two adiabatic or two thermal-contact strokes to be symmetric by setting Ma=Mband Mc=Mh, as we only focused on clarifying on the role of inner friction on the stability of machine.The extension of the present analysis to the case when these dissipations are asymmetric could be the next step in order for the role played by the dissipation along each process to be better understood, not only for a refrigerator[42] but also for a heat engine [40, 41].Another natural extension of our work would be the stability analysis of quantum thermal machines.For quantum systems with inner friction, the time-dependent entropy generation along the thermodynamic adiabatic(but not quantum adiabatic)process can be determined by unitary transformations [34], and a generalization of our calculation to the quantum machines might be an interesting issue for future research.Such a topic would be also useful for understanding the dynamical control on the nonequilibrium quantum systems.
杂志排行
Communications in Theoretical Physics的其它文章
- Impact of Joule heating and multiple slips on a Maxwell nanofluid flow past a slendering surface
- Generating a dynamical M2 brane from super-gravitons in a pp-wave background
- Uncertainty relation of successive measurements based on Wigner–Yanase skew information
- Quantum uncertainty relations of Tsallis relative α entropy coherence based on MUBs
- Performance of passive decoy-state quantum key distribution with mismatched local detectors
- Quasi-exactly solvable decatic model description of nuclei near the X(5) critical point
