Investigation of vortex arms in electron vortices by counter-rotating elliptically polarized attosecond laser pulses

Zhuo Wang, Qi Zhen, Yue Sun, Jia-He Chen and Xue-Shen Liu,∗

1 Institute of Atomic and Molecular Physics, Jilin University, Changchun 130012, China

2School of Civil Engineering, Changchun Institute of Technology, Changchun 130012, China

Abstract We theoretically investigate the vortex patterns in photoelectron momentum distributions of He+driven by counter-rotating elliptically polarized, time delayed attosecond laser pulses by numerically solving the two-dimensional time-dependent Schrödinger equation.It is found that the number of vortex arms is extremely sensitive to the ellipticity and wavelength of counterrotating elliptically polarized laser pulses, which is illustrated by the attosecond perturbation ionization models.In addition, the effect of different time delays between two pulses on the interference patterns is also investigated and the corresponding physical mechanism is demonstrated.Since the wavelength, ellipticity and time delay have a significant effect on the vortex interference patterns, this may be a new method for laser field detection.

Keywords: vortex arms, photoelectron momentum distributions, elliptically polarized laser pulses

1.Introduction

The rapid development of ultra-short laser pulse technology makes it possible to explore the electron dynamics on the attosecond time scale [1].Recently, the shortest single pulse with a duration of 43 as has been achieved [2], which provides a more useful tool for investigating attosecond imaging[3].In the field of strong field physics,the interaction of laser with atoms and molecules can produce a series of novel physical phenomena related to the electron ionization,such as high harmonic generation [4], nonsequential double ionization [5, 6], and above-threshold ionization [7].Therefore,electron dynamics can be better explored by investigating the photoelectron momentum distributions (PMDs) closely related to photoionization [8].

For a long time, researchers have paid great attention to the research of PMDs in the fields of atomic, molecular, and optical physics[9,10].Different types of laser fields are used to interact with atoms and molecules, so that the various electronic dynamics information of atoms or molecules can be reflected by the PMDs[11].Therefore,it has been extensively investigated both theoretically [12–14] and experimentally[15].Typical laser fields include single color or two colors[16–18], orthogonally or elliptically polarized [19, 20], and infrared or ultraviolet laser [21, 22].Polarized gated (PG)pulses [14] are used to separate and identify the intracycle interference in the PMDs of argon atoms.The researchers concluded that the PG pulses play an important role in separating various intracycle interference.The PMDs of hydrogen molecular ions were studied experimentally and it was found that the standard enhanced ionization map needs to be modified [15].

Based on Ramsey interference generated by electron wave packets in a linearly polarized laser field [23], the Ramsey interference with new characteristics by counterrotating circularly polarized laser field has recently been discovered, which presents a vortex structure in PMDs[24–26].Djiokap et al [24] studied the electron vortices of helium atoms under counter-rotating circularly polarized laser pulses with time delay for the first time.The results show that the vortex structure of the PMDs is sensitive to the time delay,relative phases, and helicity of laser pulses.That led to an extensive investigation of electron vortices.The influence of different electronic states as initial states on the vortex patterns in the PMDs[27]has been deeply discussed.The Stark effect on the vortex interference patterns[28]has been studied theoretically, and it is found that the quantum effect can distort the vortex structure.Experimentally, The electron vortices of potassium atoms [29] in a counter-rotating circularly polarized laser field were explored by researchers.It is worth noting that, the experimental results were highly consistent with the theoretical results.

In this paper, we investigate the effects of different laser parameters of the counter-rotating elliptically polarized attosecond laser pulse on the interference patterns in the PMDs of He+.Numerical results show that the number of vortex arms depends on the ellipticity and wavelength of the laser pulse,and the number of vortex arms decreases significantly with the decrease of ellipticity or wavelength.In addition, the PMDs under different time delays are compared, and the physical mechanism of the corresponding changes in the number of vortex arms is discussed.

The paper is organized as follows: we introduce our theoretical model and computational method briefly in section 2.The computational results in different cases are presented and analyzed in section 3.Finally, a summary is given in section 4.Atomic units e=ħ=me=1 are used throughout, unless indicated otherwise.

2.Model and method

We investigate the PMDs when He+is exposed to a pair of left-right elliptically polarized attosecond laser pulses.The two-dimensional (2D) time-dependent Schrödinger equation(TDSE)under the dipole approximation and the length gauge can be written as

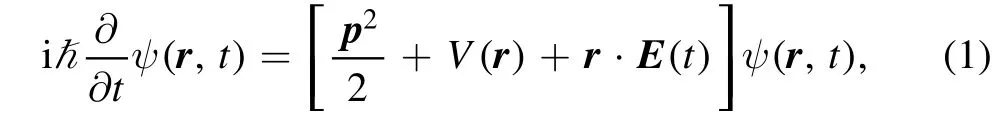
where r and p are the coordinate and momentum operator of the electron.The soft-core Coulomb potential V(r) can be expressed as

The soft-core parameters b=2.0 and a=0.169 are adopted.The corresponding energy eigenvalue of the ground state is Ip=2.0 a.u.The counter-rotating elliptically polarized driving laser field in our simulation can be written as

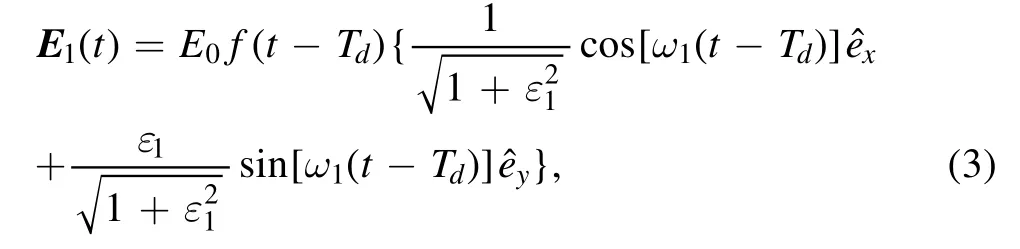
and

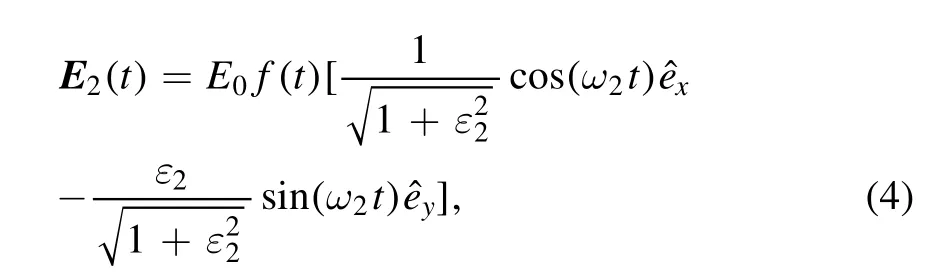
where ε1and ε2are the ellipticity of the polarized laser pulse,and Tdis the time delay between two pulses.f(t) = exp [ −2 (ln 2)t2/τ2]is the envelope function of the laser pulse with a total duration of ten optical cycles.The full width at half-maximum (FWHM) τ=2T(T=2π/ω1), and ω1,2are the angular frequency of both pulses.The amplitude of the laser pulse is I0=5×1014W cm−2(E0=0.12 a.u.).

To numerically solve 2D TDSE,we use the split operator method[30]and fast Fourier transform technology.The initial wave packet is obtained by the imaginary time propagation method.

The length of the integration grid is fixed at 409.6 a.u.and the spatial discretization is 0.4 a.u.The absorption range of 150 a.u.≤|x,y|≤204.8 a.u.is set to prevent non-physical effects due to the reflection of electron wave packets from the boundary.And for every time step in the absorption range,the wave function is multiplied by the cos1/8‘mask function’.The wave function of the electron wave packet of the ionized part at the final time is expressed as [1 −M(r)]φ(x, y, tf),where φ(x, y, tf) is the wave function at final time, and the mask function can be expressed as

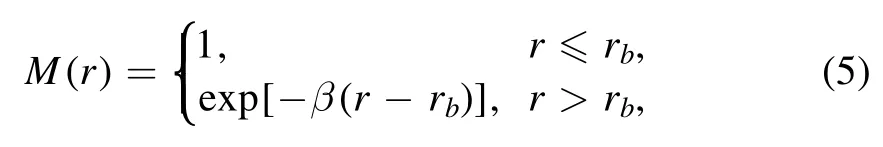
where β=1 a.u.The boundary for the ionized wave function and bounded wave function is fixed at rb=15 a.u.After the laser pulse ends, we propagate the wave function for another two optical cycles.The PMDs can be obtained by Fourier transform from the ionized wave function at the final time.

3.Results and discussion

To investigate the factors that affect the vortex patterns, we demonstrate the PMDs of He+by counter-rotating elliptically polarized laser field under different laser parameters.

We first consider the case where ε1=ε2.Figure 1 shows the simulated results of PMDs at different ellipticities by counter-rotating elliptically polarized laser pulses.The wavelengths of both pulses are λ1=λ2=80 nm(ω1=ω2=0.57 a.u.),and the time delay is fixed at 3 o.c.The FWHM is set as 2 o.c.Figure 1 displays the PMDs of He+with different ellipticities (ε1=ε2=1.0 [figure 1(a)],ε1=ε2=0.75 [figure 1(b)], and ε1=ε2=0.5 [figure 1(c)]).It can be seen that there are eight,six and four vortex arms in figures 1(a)-1(c),respectively.As the ellipticity decreases,the number of vortex arms in the clear interference patterns gradually decreases.It means that the number of vortex arms can be effectively controlled by changing the ellipticity of the laser pulses.

Next, we use the attosecond perturbation ionization model[31, 32] to illustrate the interference patterns in the PMDs of He+as shown in figure 1.Because the helicity of the two pulses is opposite, the electron can be simultaneously ionized into the continuum state via two ionization channels and reach the same final energies.And the ionization process of He+is the fourphoton ionization process due to(4ω>Ip=2.0 a.u.).According to the attosecond perturbation ionization models, the transition amplitude for the four-photon ionization of left-rotating circularly polarized laser pulse can be expressed as [24, 33]

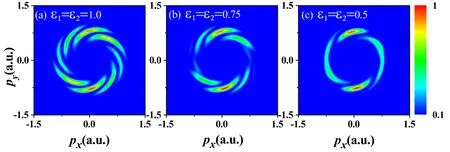
Figure 1.PMDs of He+ by counter-rotating elliptically polarized laser pulses with the ellipticity (a) ε1=1.0, ε2=1.0 (b) ε1=0.75,ε2=0.75 (c) ε1=0.5, ε2=0.5, which are delayed in time by 3 o.c.(799as).Pulse intensity I0=5×1014 W cm−2 (E0=0.12 a.u.).FWHM=2 o.c.(533as), and wavelength λ1=λ2=80 nm (ω1=ω2=0.57 a.u.).

where Ek,Emand Enare the energy of the intermediate(virtual)electronic state and Γk,Γmand Γnare the level width.Since the denominator is a constant,we can write the transition amplitude in the form of equation (6).ψk, ψmand ψnare the intermediate states of He+.ψ0,ψcare the initial state and continuum state of He+.D is the electric dipole operator.For the convenience of calculation, we write it as the product of a scalar D and a unit vector n,i.e.D=nD.n represents the direction of the transition dipole moment, and the angle between it and the x axis is defined as the exit direction of the photoelectron.E1(ω)=e1E1(ω) represents the Fourier transform to frequency space of the laser pulse E1(t), and e is the polarization vector.η1=φ1is the total phase of left-rotating circularly polarized laser pulse.Decomposing the expression of transition amplitude,the transition matrix element σ(1)of four-photon ionization from ground state ψ0to continuum state ψchas the form

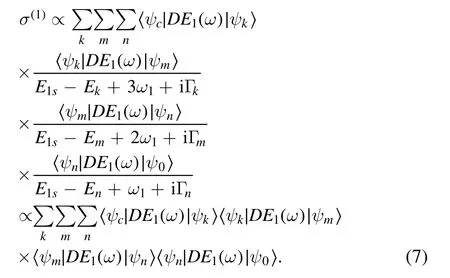
The corresponding scalar product

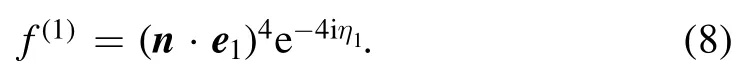
The total phase of left-rotating circularly polarized laser pulse is η1=φ1.

In the same way, the transition amplitude of the electron interacting with right-rotating circularly polarized laser laser pulse can be written as

where the scalar product

Since left-rotating circularly polarized laser pulse has a time delay relative to right-rotating circularly polarized laser pulse,the total phase of right-rotating circularly polarized laser pulse is η2=φ2−ωTd, which describes the corresponding angular distributions of PMDs.

For the case of ε1=ε2=1.0, (n·e) can be written as[31, 32]

where θ is the ejection angle of photoelectron.The ionization probability of He+can be written as

|W(1)|2and |W(2)|2represent the ionization probability only under the interaction of left-rotating or right-rotating circularly polarized laser pulse.W(1,2)is the interference term,which can be written as

the angular scalar product f(1,2)can be expressed as

The total phase difference between the two laser pulses can be expressed as Δη=4η1−4η2.According to the conservation of energy in the case of four-photon ionization, the energy absorbed by the electron from the laser field is 4ω,i.e.p2/2 −E1s=4ω.Where p2/2 is the kinetic energy of the photoelectron, and E1sis the energy of the ground state of He+.Therefore, Δη=4(φ1−φ2)+4ωTd=4ωTdis the total phase difference between two pulses.(We set the carrier envelope phase of the two lasers to be φ1=φ2=0.)

When the interference term takes the maximum value,θ=nπ/4+Δη/8,n=(0,1,2,…).We can calculate exactly the extreme interference of the PMDs occur at θ=19°, 64°,109°, 154°, 199°, 244°, 289°, 334°.Therefore, the PMDs of He+at ε1=ε2=1.0 have eight vortex arms,which is in good agreement with that as shown in figure 1(a).And the rotating direction is consistent with the rotation direction of the second laser pulse.The combined action of the laser field and the Coulomb potential results in a small rotation angle of PMDs.The contribution of the ionization cross channel [34] will work within a short time delay.As a result, this will cause a difference in the brightness of the vortex interference patterns.

For the case of ε1=ε2=ε ≠1, the transition amplitude for left-rotating elliptically polarized laser pulse can be expressed as

to approach the probability of absorbing photons.

Thus the number of left-rotating photons absorbed in the left-rotating elliptically polarized pulse can be approximatelywhereis the average helicity of left-rotating elliptically polarized pulse.The number of right-rotating photons absorbed in the right-rotating elliptically polarized field is similar to that illustrated above.

The contribution of photons absorbed from left-rotating elliptically polarized laser pulse to the scalar product can be written similarly as

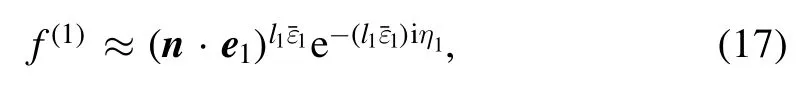
where l1is the number of elliptically polarized photons absorbed by electrons reaching a continuum state in leftrotating elliptically polarized laser pulse.η1is the total phase of left-rotating elliptically polarized laser pulse.

In the same way, the transition amplitude of the electron in the interaction of right-rotating elliptically polarized laser pulse can be written as

the scalar product

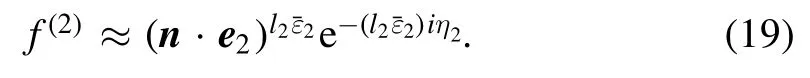
The interference term can be written as

where the angular scalar product f(1,2)can be expressed as

Δη is the total phase difference between two pulses.When the wavelength of the laser is 80 nm,the ionization process is that the electron absorbs four photons to reach a continuum state, i.e.l1=l2=4.

To better understand the influence of the ellipticity on the vortex patterns of He+, we investigate the case that ε1≠ε2.Except that the laser wavelength and the absorption boundary for ionized wave function are chosen as 100 nm and rb=60 a.u., the other laser parameters are the same as those in figure 1.When the wavelength is 100 nm, the ionization process is five-photon ionization(l1=l2=5).In figures 2(a)–(c),we show the PMDs of He+by counter-rotating elliptically polarized laser pulses with different ellipticities (ε1=1.0 ε2=1.0 [figure 2(a)], ε1=0.6 ε2=1.0 [figure 2(b)], and ε1=0.4 ε1=0.8 [figure 2(c)]).It can be seen that the corresponding number of vortex arms is ten, eight and six,respectively.We also use the attosecond perturbation ionization model to illustrate the variation of the number of vortex arms in the PMDs as shown in figure 2.Considering that in a counter-rotating circularly polarized laser field, the interference term reads

According to equation (21), we can get the angular scalar product

the maximum interference term appears at

This means that ten vortex arms appear in the interference patterns,which is in agreement with that shown in figure 2(a).

Figure 2.PMDs of He+by counter-rotating elliptically polarized laser pulses with the ellipticity(a)ε1=1.0 ε2=1.0,(b)ε1=0.6 ε2=1.0,(c) ε1=0.4 ε2=0.8, which are delayed in time by 3 o.c.(1013as).Pulse intensity I0=5×1014 W cm−2 (E0=0.12 a.u.), FWHM=2 o.c.(675as), and wavelength λ1=λ2=100 nm (ω1=ω2=0.45 a.u.).

We can conclude that the number of vortex arms in the interference patterns decreases with the decrease of the ellipticity.And the numerical results shown in figure 2 are in good agreement with the predictions in equation (21).

We further investigate the effect of the pulse wavelength on the vortex interference patterns in PMDs by counter-rotating elliptically polarized laser pulses.The ellipticity of two pulses is set as ε1=ε2=0.5, and other parameters are the same as those in figure 1.Figure 3 shows the vortex interference patterns in PMDs of He+by a pair of counter-rotating elliptically polarized laser pulse at the wavelength of (a) λ1=λ2=120 nm, (b) λ1=λ2=80 nm,and (c) λ1=λ2=20 nm.

We can see that there are six-start vortex structure in figure 3(a),four-start vortex structure in figure 3(b),and twostart vortex structure in figure 3(c).The electron will absorb different numbers of photons to reach a continuous state due to the different wavelength.For λ1=λ2=120 nm(ω1=ω2=0.38 a.u.), the ionization process is six photon ionization(6ω>Ip).When the wavelength changes to 80 nm,the electron needs to absorb four photons (4ω>Ip) to reach the continuum state.According to equation (21), we can get θ=nπ/3+Δη/6 and θ=nπ/2+Δη/4, n=(0, 1, 2, …),respectively.It means that there are six/four-start vortex structure as shown in figures 3(a) and (b).

Since photons are the smallest unit of energy, electrons cannot absorb less than one photon to ionize.Thus single photon ionization results in two vortex arms as shown in figure 3(c).As the wavelength decreases, the number of vortex arms in the PMDs also decreases significantly.In other words,the wavelength can play a major role in regulating the vortex arms in the MPDs of He+.

Figure 3.The vortex interference patterns in PMDs of He+by a pair of counter-rotating elliptically polarized laser pulse at the wavelength of(a) λ1=λ2=120 nm, (b) λ1=λ2=80 nm, and (c) λ1=λ2=20 nm.The time delay Td=3 o.c., the ellipticity of the two pulses is ε1=ε2=0.5.Pulse intensity I0=5×1014 W cm−2 (E0=0.12 a.u.), and FWHM=2 o.c.

We finally investigate the vortex interference patterns of He+by counter-rotating elliptically polarized attosecond laser pulses with different time delays(a)Td=0 o.c.,(b)Td=2 o.c., (c) Td=2.3 o.c., and (d) Td=3 o.c., which are shown in figure 4.The ellipticity of the two pulses is set as ε1=0.6 and ε2=1.0.The wavelength is 100 nm (ω1=ω2=0.45 a.u.).The other parameters are the same as those in figure 1.

It is found that no vortex structure is generated in the PMDs for the time delay Td=0 o.c.as shown in figure 4(a).The PMDs has maximum values along the four directions.As the time delay is increased to Td=3 o.c.,the PMDs gradually evolves from unstable vortex structure to stable vortex structure, as shown in figures 4(b)–(d).In addition, it is easy to find that the length of the vortex arms is gradually extended as the time delay increases.

To further understand the reason of the stability of vortex arms, we give a detail analysis of the process of gradual formation of the vortex arms When the time delay is equal to 0 o.c., since the two laser pulses used in the paper have the same frequency, the two counter-rotating circularly polarized laser pulses are combined into

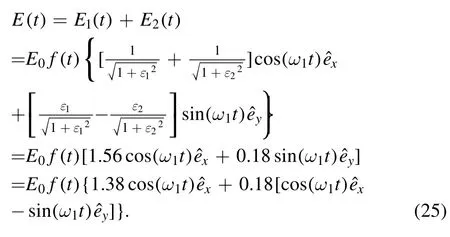
It can be seen from equation(25)that the combined laser is divided into a linearly polarized laser and a circularly polarized laser.At this time,the intensity of linearly polarized laser is much greater than that of circularly polarized laser.Therefore, the PMDs are mainly distributed along the laser polarization direction, so there is almost no vortex structure generated.When the time delay starts to increase, since the two elliptical polarization pulses with time delay have opposite rotation, the electron wave packets ionized through the two ionization channels have opposite spatial orientation.Therefore,the PMDs mainly distributed along the x direction begins to twist, and the vortex structure becomes more and more obvious.This directly causes that six unstable vortex arms appear in the PMDs when Td=2 o.c.Therefore, it can be seen that there is a big difference in the width and strength of the vortex arms,which means that the vortex arms formed at this time are unstable as shown in figure 4(b).Similarly,we found that a pair of vortex arms in the PMDs begin to split at Td=2.3 o.c., resulting in eight stable vortex arms at Td=3 o.c.Due to the time delay between two pulses, the formation of the vortex patterns is accompanied by the distortion of the PMDs.With the increase of the time delay, the time of the electron traveling is correspondingly prolonged.This leads to an extension of the electron’s range of motion,and the increase in the length of the vortex arms is well explained.

Figure 4.PMDs of He+by a pair of counter-rotating elliptically polarized attosecond laser pulses with different time delays(a)Td=0 o.c.,(b) Td=2 o.c., (c) Td=2.3 o.c., and (d) Td=3 o.c., respectively.The intensity of pulse is I0=5×1014 W cm−2 (E0=0.12 a.u.), and FWHM=2 o.c.The ellipticity of two pulses is set as ε1=0.6 and ε2=1.0, and the wavelengths are λ1=λ2=100 nm(ω1=ω2=0.45 a.u.).

4.Conclusions

In summary, we theoretically investigate the vortex patterns in PMDs of He+driven by a pair of left-right elliptically polarized, time delayed laser field by numerically solving the 2D TDSE.The vortex patterns show the dependence on the ellipticity of the elliptically polarized laser pulse.As the ellipticity decreases, the number of vortex arms in the clear interference patterns gradually decreases.This conclusion is confirmed in both ε1=ε2and ε1≠ε2cases.We also compare the effect of wavelength of laser pulse on the vortex structure.Results show that the number of vortex arms decreases as the wavelength(the number of photons absorbed by the electron)decreases.Finally, the effect of time delay on the PMDs is discussed.As the time delay increases, the number of vortex arms in the clear interference patterns also increases, and we discuss the physical mechanism of the increase in the number of vortex arms.This result demonstrates an unusual control of vortex interference patterns in the attosecond time scale.The numerical results are analyzed by attosecond perturbation ionization theory.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grants No.12074142).