Charged black holes in the infinite derivative theory of gravity

Yong Xiaoand Longting Zhang

Key Laboratory of High-precision Computation and Application of Quantum Field Theory of Hebei Province, College of Physical Science and Technology, Hebei University, Baoding 071002, China

Abstract The infinite derivative theory of gravity is a generalization of Einstein gravity with many interesting properties,but the black hole solutions in this theory are still not fully understood.In the paper, we concentrate on studying the charged black holes in such a theory.Adding the electromagnetic field part to the effective action, we show how the black hole solutions around the Reissner–Nordström metric can be solved perturbatively and iteratively.We further calculate the corresponding temperature, entropy and electrostatic potential of the black holes and verify the first law of thermodynamics.

Keywords: quantum aspects of black holes, black hole thermodynamics, modified theories of gravity

1.Introduction

Einstein’s general relativity has gained a lot of success since it came into being.However, in the spirit of effective theory,one can add all the possible diffeomorphism invariant curvature terms to the Einstein–Hilbert action, thus modifying the original Einstein gravity.Moreover,the modified theories of Einstein gravity are also motivated by explaining the cosmological problems,such as the early inflationary era and the present accelerating expansion of the Universe [1].

Nowadays, modified gravity has become a large area with many kinds of formalism and applications.In particular,the fourth order gravitational theory is proved to be renormalizable but is disturbed by the ghost propagators[2].To get a renormalizable and ghost-free theory, one should introduce an infinite number of higher curvature or derivative terms[3, 4].In the paper, our attention is focused on an infinite derivative theory of gravity (IDG), which was proposed and developed in [5–9].The theory modifies the Einstein gravity at small scales through the infinite higher derivative terms that are added to the effective action,which can also be viewed as higher order quantum gravitational corrections.It recovers to Einstein gravity in the infrared, while the massless gravitons are the the only propagating degrees of freedom under an appropriate ghost-free condition.

As is known, black hole physics plays a significant role in the study of quantum gravitational effects,so it is meaningful to investigate the properties of black hole solutions in the IDG.Generally, if the higher derivative terms have been taken into account in the modified gravity,the original black hole solutions in Einstein gravity cannot be the exact solutions anymore; they must receive appropriate corrections.In fact, due to the highly complexity of the effective action of such an infinite derivative theory, almost all the previous analyses were around the Minkowski space-time,as well as cosmological backgrounds[6,7].Only very recently,Xiao et al[10]considered the Schwarzschild black hole in the IDG,and successfully obtained the corrections to the black hole metric and the thermodynamics.

In the paper,we move forward to analyze the charged black holes in the IDG.The significance of the work is as follows.First, we shall solve the corrections to the Reissner–Nordström(R-N)metric and the corresponding thermodynamic quantities in the IDG.Actually,the topic started from[8],which asserted that the entropy corrections to the area law for any spherically symmetric black hole vanish,but the assertion is problematic and was modified to some extent in its Erratum.As shown in [10], in order to provide a fully consistent thermodynamic analysis, it is important to solve the black hole solutions from the gravitational field equations.Such an analysis about the Schwarzschild black hole has been fulfilled in [10].In this paper, another spherically symmetric black hole,i.e.the R-N case will also be investigated,which may further improve the understanding of the topic.Second,compared to the Schwarzschild case,now the gravity is coupled with matter (electromagnetic fields in this case).In the absence of a matter field,the first order perturbation of the theory involves only the Riemann tensor part,but once the matter field is involved,the Ricci tensor will also contribute[11,12].In this way,the interaction between the higher order curvature terms and the matter fields will be better understood.It also demonstrates that the methods of [10] can be applied to even more general situations beyond the pure gravitational case.Third, extremal black hole is important in counting quantum micro-states of black holes [13].And our work can pave a way to discuss the properties of extremal black hoes in the IDG.

The paper is organized as follows.We first review the essential ingredients for the study of the IDG, including the effective action and the gravitational field equations.Next we show how the field equations can be solved around the R-N metric perturbatively and iteratively.We also analyze the thermodynamic quantities of the charged black holes.Finally,we close the paper with a summary and discussion.

2.Effective action and field equations of the IDG

At second order in curvature, the effective action of the IDG has the form

where we have taken the Ricci scalar, Ricci tensor and Weyl tensor as the independent curvature bases.The parameter α has the dimension of inverse mass squared, and it controls the overall effects of the higher order terms Its value may be constrained by the future astronomical and cosmological data[14, 15].F1,F2andF3are analytic functions of the D’Alembertian operatorwhich can be expanded as Obviously,in the action of the IDG,there are an infinite number of derivatives acting on the spacetime curvature.The coefficientsfi,nshould satisfy a ghost-free condition to make sure that the massless gravitons are the only propagating degrees of freedom [8, 9].

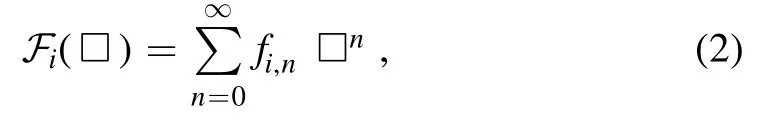
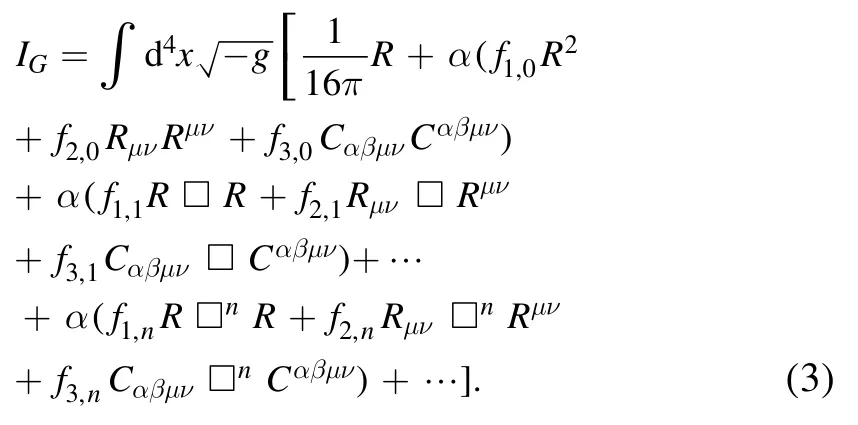
Adding the electromagnetic field part to the effective action, the complete action is

where

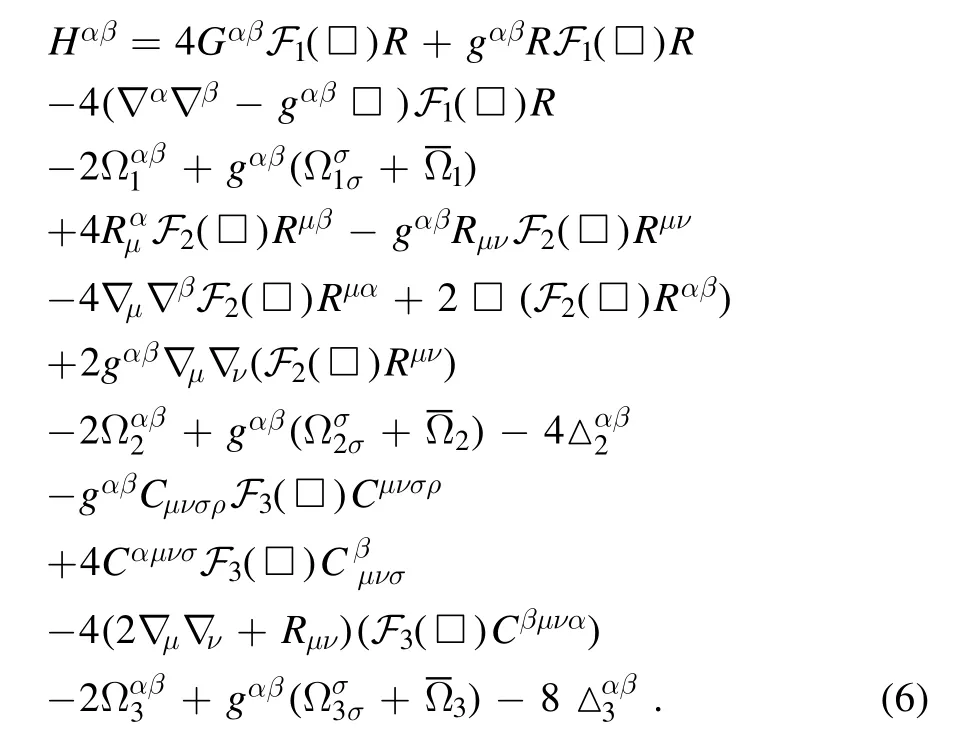
The detailed definition of the symbols Ωi,and Δican be found in[6].The electromagnetic energy-momentum tensor is

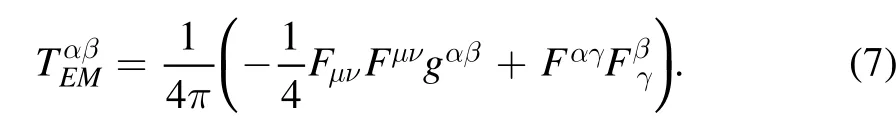
Notice we adopt a convention with an extrathat is often used to simplify the R-N metric.

3.Black hole solutions around R-N metric

In this section we analyze the gravitation field equations of the IDG and solve them perturbatively around the R-N metric.The procedure is as below.First, we consider the solution with the form

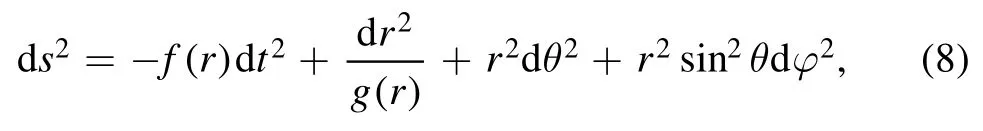
with

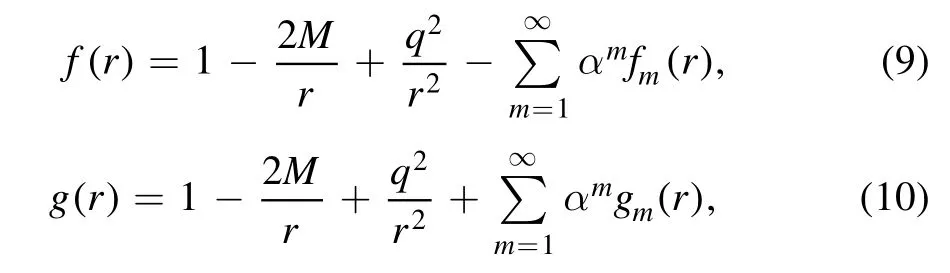
where fm(r), gm(r) are the unknown functions to be solved.Clearly, the original R-N metric is used as the zeroth order approximation,then we substitute it into the gravitational field equations and study them at the first order of the parameter α.After solving the metric at the orderO(α),we further use it as the first order approximation, and solve the metric from the field equations at the orderO(α2) , and so on and so forth.In this way,we can obtain the black hole solutions of the IDG up toO(αn) perturbatively and iteratively.The final outcome can be written as the R-N metric added by a series of α (or equivalently the Taylor coefficientsfi,n).In practice, the first several order result may be enough for many purposes.

Now, we start to investigate the influence of the higher derivative terms in the action(3)line by line.Actually the first line of(3)gives the usual quadratic gravity.Since the charged black hole in the quadratic gravity has been the topic of[16, 17], we will not repeat the task.We start from thefi,1□(i= 1, 2, 3) terms in the second line of (3).Substituting the metric (8) into equations (5) and (6) and keeping only the terms linear infi,1(i= 1, 2, 3),after a tedious simplification,we have the rr components of the gravitational equations as

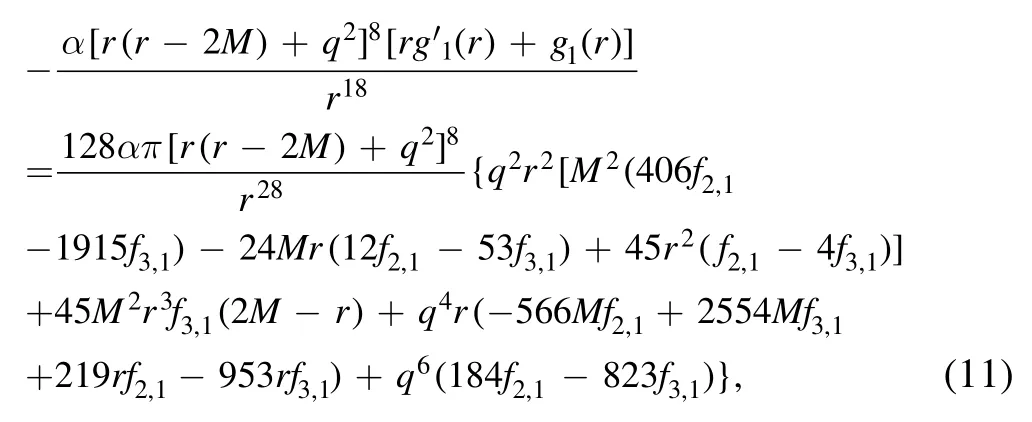
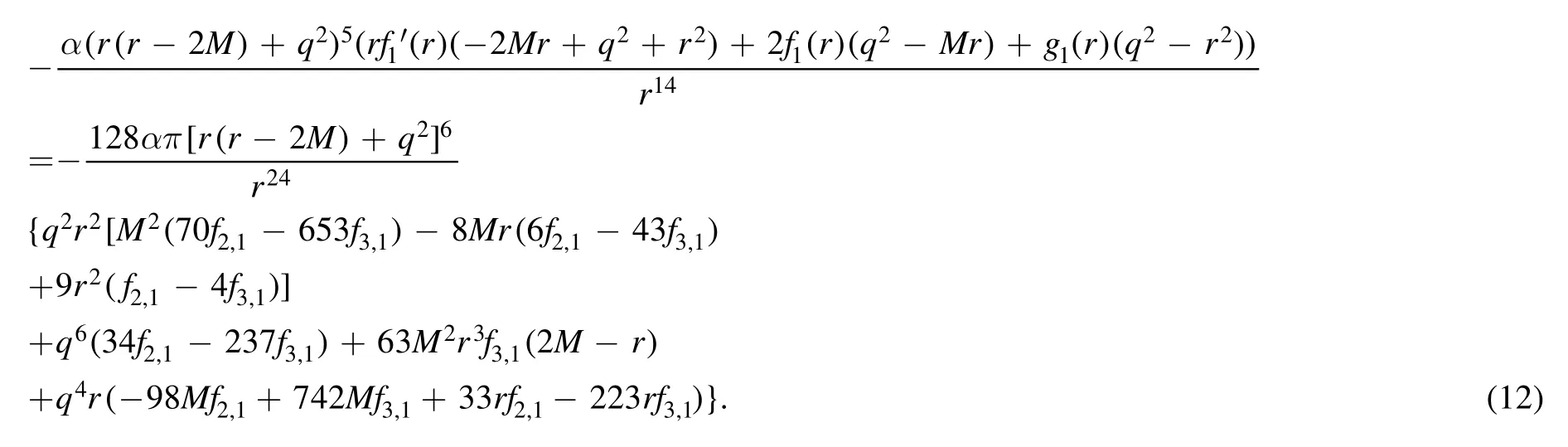
From these equations, we solve the functionsf1(r)andg1(r)related to thefi,1□part of the action.Thus,the corresponding metric atO(α) is given by

The other nonzero components of the gravitational field equations are confirmed by explicitly inserting the obtained metric into them.Besides, because R = 0 for the original R-N black holes, the coefficientf1,1does not contribute at the first order.As illustrated, we can go further to solve the metric iteratively to higher order of α, but the calculations are far more complicated.So we only make some discussions about the second order results and present a simple example in the appendix.With the solution at hand, one may concern about its stability.But the stability of black holes in the modified gravity is hard to examine.Even for a relatively easier case,i.e.the gravitational theory with curvature-squared terms, the stability analysis under metric perturbation is unknown [18].To say the least, in the present cases, it would always be possible to choose appropriate signs for the parametersfi,nʼs to ensure the stability of the black hole solutions.

Next we study the corresponding corrections to the black hole thermodynamics.Takingf(r+)=0 andg(r+)=0, we will get the relation between the mass M and the outer horizon radius+rof the black hole.Notice f(r) and g(r) in (13) and(14)are rather complicated third-order algebraic equations for M,so a directly computation is extremely difficult.However,we only need a solution around the R-N metric and take α a small parameter for Taylor series expansion,especially at first order in α,with the formFinally,we get Amazingly, though the equationsf(r+)=0 andg(r+)=0 have different forms, the solution for M is unique.This reflects the physical consistency of our calculation: generally f(r) and g(r) in the black hole metric do not have the same form, but at the radius of the horizon they must vanish simultaneously (see for example [19]).

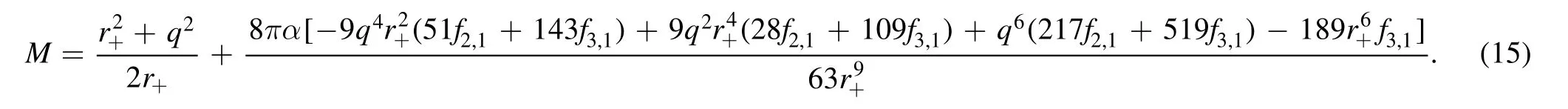
The temperature of the black hole is

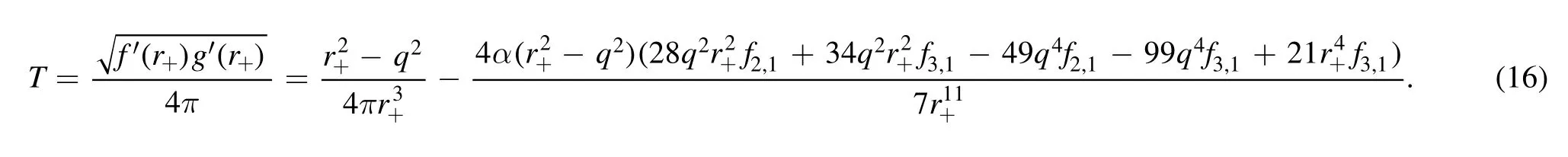
For convenience, we have used+rinstead of M as the variable for analyzing the black hole thermodynamics.The formula(16)comes from analyzing the conical singularity of the black hole metric.There is another formulawhich comes from the surface gravity.It is easy to show they produce the same result at the horizon from the L’ Hospital’s rule in computing the limit.

The electrostatic potential at the black hole horizon can be calculated fromwithA0=It gives

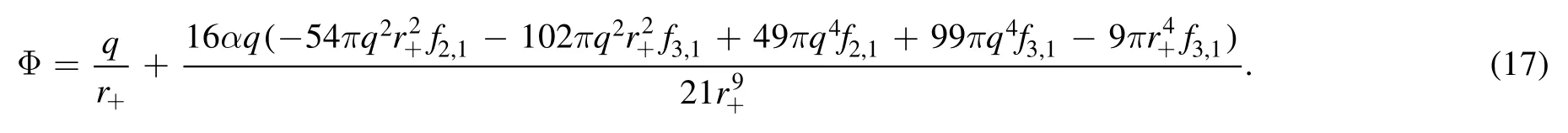
It is easy to check that the thermodynamic lawTdS+ φ dq=dMholds atO(α), according to equations (15)–(19).It is amazing to see these tedious calculations bring about such a neat relation.

For the special case with charge q = 0,the result reduces to that of the Schwarzschild case [10].Furthermore, our R-N result now enables us to consider another important extremal limit withq→r+, which is significant in exploring the microscopic aspects of the black hole entropy.From equations (16) and (19), we find that the temperature and the entropy for the extremal black hole become T = 0 andCuriously,the corrections to the entropy vanish and the entropy is given solely by the famous area lawin sharp comparison with the Schwarzschild case[10].It implies that the extremal black hole is very particular in the the study of the microscopic degrees of freedom.

The black hole entropy can be computed by using the Wald formula [20, 21]

Then the Einstein–Hilbert action produces the area law of the black hole entropy and the higher order curvature terms produces the corrections,which is a standard calculation[22].Thus we get

At first the wily fox refused to tell her what he had gathered from the conversation of the birds, but at last he gave way to her entreaties28, and told her that they had spoken of the misfortunes of a beautiful young Prince, whom a wicked enchantress had turned into a snake for the period of seven years

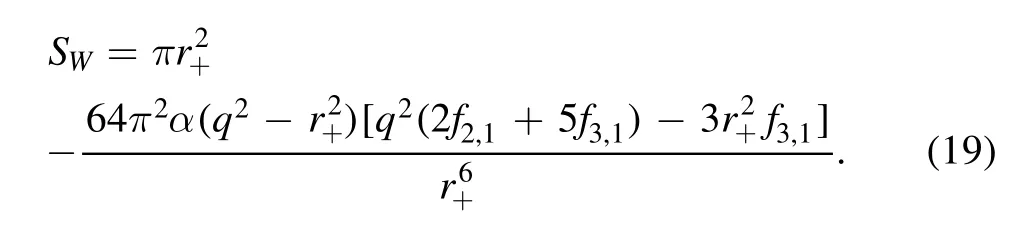
4.The fi,2□2 terms of the action and the black hole solutions

We can proceed to study thefi,2□2(i=1, 2, 3)terms in the action and solve the related part of the metric.The procedure is very similar as before, so we skip the concrete steps and provide the modified metric directly as

The corresponding corrections to the mass, temperature,electrostatic potential and entropy are respectively

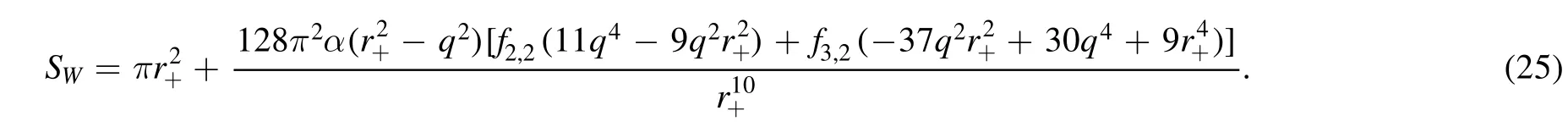
5.Conclusion

We have obtained the charged black hole solutions around the R-N metric in the IDG.The gravitational field equations (5) and(6) appear to be complex and formidable, however, our work shows that they can still be solved perturbatively and iteratively in a standard way.Technically,the main feature of the IDG is the manipulation of the operator □nin the action.In this paper, we have only provided the results for thefi,1□andfi,2□2(i= 1, 2, 3)terms in the action,but the procedure can be easily generalized to study the arbitraryfi,n□nterms.The higher derivative terms in the action have caused the corrections to geometric quantities such as the black hole metric and the horizon radius,as well as the thermodynamic quantities.Amazingly,the corrections to these quantities balance each other carefully and finally safeguard the first law of the thermodynamics.

In contrast to the Schwarzschild case [10], we have considered the interaction between the modified gravity and the electromagentic fields.The electrostatic potential has to be taken into account in analyzing the thermodynamic law.Furthermore, our result enables us to study the important extremal case withq→r+, and the result shows that the corrections to the area law of the black hole entropy vanish,which is very interesting and may have deep implications.Our work has improved the understanding of black hole solutions and the corresponding thermodynamics in the IDG,and also made necessary technical preparations for the future research on more general black hole backgrounds.

Acknowledgments

The authors would like to thank Yong Chen for useful discussions.The work was supported in part by the NSF of Hebei province with Grant No.A2021201022.

AppendixIn the IDG,if considering all the derivative terms at one time,the corrections to the metric and the thermodynamic quantities can be classified according to the order of α.The terms proportional toαfi,nare collected inO(α),and the terms proportional toandare collected inO(α2) ,so on and so forth.In the paper, we mainly did the leading order calculation ofO(α) for the □and □2operators.These operators can be studied independently at the leading order and the results are linear in the corresponding Fourier coefficientsfi,n.However, when we proceed with the higher order calculation,the results have to contain the cross-product terms ofrepresenting the interactions among these operators.

In the appendix,we aim to exhibit the cross-product term ofas an example.It is related to the interaction betweenandWe have set q = 0 in presenting the results below, because the expressions with nonzero q are too complicated.Whatever,one can compare them with equations (13), (14), (20) and(21)(setting q=0)and observe that the leading order piece is independent of the interactions.The obtained black hole metric is

The black hole mass, temperature and entropy with second order corr ections are respectively

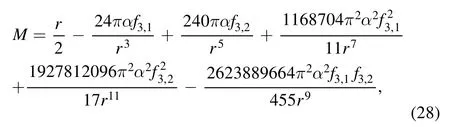
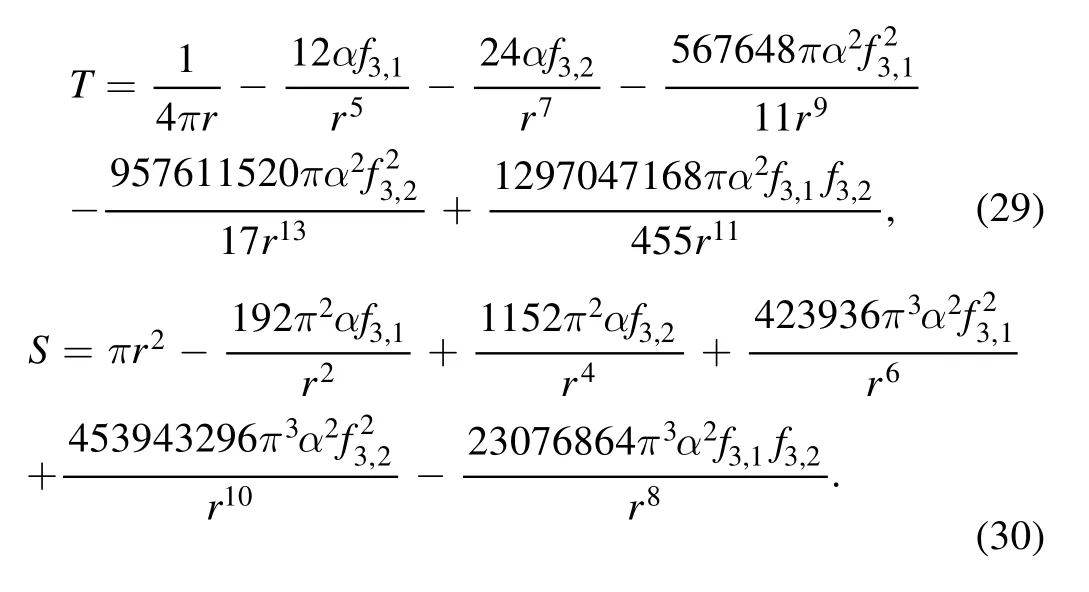
ORCID iDs