The angular momentum and parity projected multidimensionally constrained relativistic Hartree–Bogoliubov model
2022-02-18KunWang王琨andBingNanLu吕炳楠
Kun Wang (王琨) and Bing-Nan Lu (吕炳楠)
1 CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190, China
2School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
3 Graduate School of China Academy of Engineering Physics, Beijing 100193, China
Abstract Nuclear deformations are fundamentally important in nuclear physics.We recently developed a multidimensionally constrained relativistic Hartree–Bogoliubov (MDCRHB) model, in which all multipole deformations respecting the V4 symmetry can be considered self-consistently.In this work we extend this model by incorporating the angular momentum projection and parity projection to restore the rotational and parity symmetries broken in the mean-field level.This projected MDCRHB(p-MDCRHB)model enables us to connect certain nuclear spectra to exotic intrinsic shapes such as triangles or tetrahedrons.We present the details of the method and an exemplary calculation for 12C.We develop a triangular moment constraint to generate the triangular configurations consisting of three α clusters arranged as an equilateral triangle.The resulting 12C spectra are consistent with that from a triangular rigid rotor for large separations between the α clusters.We also calculate the B(E2)and B(E3) values for low-lying states and find good agreement with the experiments.
Keywords: nuclear physics, beyond mean field, density functional, nuclear clustering
1.Introduction
Most atomic nuclei are deformed in their ground states[1,2].The nuclear shapes can be described by the surface multipole expansion
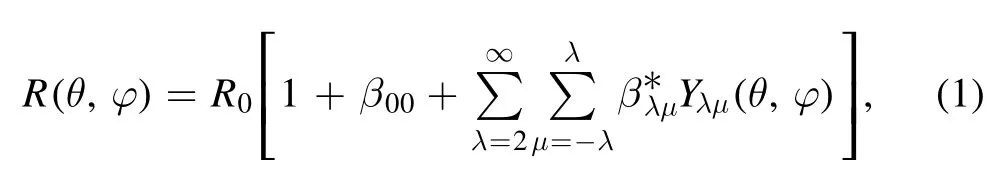
where R is the distance from the center of mass to the nuclear surface,and λ and μ are integers characterizing different kinds of multipole deformations.For example, βλ0describes axially symmetric deformations, the triaxial deformations correspond to βλμwith even λ,and the tetrahedral shape means β32≠0 while all other βλμvanish.These shape parameters can be viewed as generalized coordinates, from which we can build dynamical theories describing the rotations and vibrations of the nuclei.These collective motions are foundations of nuclear spectroscopy.
The nuclear spectra are the fingerprints of the underlying nuclear shapes.The most studied deformations are the axially symmetric quadrupole deformation with only β20≠0, which manifests itself in the typical spectra of a symmetric rigid rotor,E ∝I(I+1).A more interesting case is the triaxial deformation with non-zero β20and β22,which results in the wobbling motion[2] and the chiral doublet bands [3–5].The multiple chiral doublet (MχD) in nuclei with different triaxial configurations was predicted by Meng et al [6] and recently confirmed experimentally in several nuclei [7–11].A number of studies have shown that the low-spin signature inversion indicates the existence of triaxiality in certain regions of the nuclide chart[12–17].On the other hand, the parity-breaking octupole deformations β3μ≠0 are also found in many experiments[18–20].For example, the low-lying alternative parity bands found in actinides and some rare-earth nuclei hint the possible existence of reflection asymmetric shapes [21–28].Direct evidence of a static reflection asymmetric shape was found in224Ra [29],144Ba [30] and228Th [31].
In recent years various exotic nuclear deformations have attracted a lot of theoretical interest.For example, reflection asymmetric deformations combined with triaxial deformations have been proposed to influence the nuclear fission barrier[32–36].Nuclear clustering has been proved to be important in light nuclei, especially in the states near the nα binding threshold [37–40].Nuclear clustering configurations with various arrangements of α clusters are naturally accompanied by exotic shape deformations.It implies that a proper theoretical description requires simultaneous inclusion of various shape degrees of freedom.It has been demonstrated that the density functional theories are able to describe the clustering structure in light nuclei [41–49].The study in [41] discussed the clustering structure of light nuclei with N=Z using the axially deformed relativistic mean-field model.Using the cranking covariant density functional theory(CDFT),rod-shaped carbon isotopes at high spins were studied[48,50,51].Studies based on the algebraic model[52]and the antisymmetrized molecular dynamics model [53] suggested that the α clustering can appear in the low-lying states of12C and other light even–even nuclei [54–56].To study how nuclei cluster and how the clustering influences nuclear properties, we need theories that can describe both the excited states and the ground state, and include as many shape degrees of freedom as possible.
The CDFT gives a universal description of the nuclei all over the nuclide chart[57–65].In CDFT,the Lorentz invariance nature of the Lagrangian automatically determines the spin–orbit interaction, and reveals the origin of the pseudospin symmetry [64,66–71]in the Fermi sea and the spin symmetry in the Dirac sea[72,73].An advantage of studying nuclear clustering with CDFT is that it does not presume the existence of α clusters a priori but generates such configurations from microscopic interactions.However,the mean-field approximation used in CDFT brings the problem that the intrinsic symmetries and conservation laws,such as the translational invariance, rotational invariance, parity and particle number conservations, are usually broken [74].One solution is to restore these symmetries using the projection method; examples are the angular momentum projection(AMP)and the parity projection(PP)methods[62].By combining AMP and PP with the generator coordinate method, we can calculate the rotational–vibrational spectra,which can be directly compared with the experiments [62, 75–78].
In recent years, multidimensionally constrained CDFTs(MDCCDFTs) [33, 79–81] have been established and applied successfully in several topics.In these models, the reflection asymmetric and axially asymmetric deformations can be considered simultaneously, with only a spatial V4symmetry remaining unbroken for the densities and potentials.Depending on how to deal with the pairing correlation, two variants were developed: the multidimensionally constrained relativistic meanfield model [33, 79], and the multidimensionally constrained relativistic Hartree–Bogoliubov model (MDCRHB) [80].MDCCDFTs have been applied to study the potential energy surfaces (PES) and fission barriers in actinides [32–34, 79] and superheavy nuclei [82], the third minima on PESs of light actinides [35], higher-order deformations in superheavy nuclei [83],non-axial octupole Y32correlations in N=150 isotones[84]and Zr isotopes[80]and axial octupole Y30correlations in MχD[11].Fission dynamics in actinides were studied based on PESs calculated with the MDCCDFTs[85–89].Furthermore,by including the strangeness degrees of freedom,MDCCDFTs were employed to study the shape evolution [90, 91] and hyperon pairing correlation [92] in hypernuclei, and to build new nucleon–hyperon effective interactions [93].
In this work we focus on the MDCRHB model and its extensions.The mean-field state∣φ(q) 〉 can be obtained by solving the relativistic Hartree–Bogoliubov (RHB) equation in the intrinsic frame.Here, q is a collection of quantum numbers specifying the deformation of the state or other intrinsic properties.Several intrinsic symmetries may be broken due to the meanfield approximation and need to be restored using the symmetry projection methods.For example, the AMP for a relativistic mean-field model has been implemented upon a triaxially deformed ground state [94] and an axially deformed reflection asymmetric ground state [95, 96].The generating coordinate method(GCM)has also been included to treat soft PESs[75,76].In this work, we incorporate the AMP and PP methods into the MDCRHB model.Our implementation differs from the previous works in two aspects.First,we apply a unified framework to treat both the triaxial and octupole deformations.While in [94] the triaxial deformations are considered with an anisotropic 3D harmonic oscillator(3DHO)basis,in this work we employ an axially symmetric harmonic oscillator basis in all cases.This setting allows us to simultaneously break as many symmetries as possible and consider exotic shapes like the triangle or tetrahedron.Second, we use the Bogoliubov transformation together with a separable pairing force of finite range to treat the pairing effect.This makes our results more reliable for extreme deformations for which the pairing force can play key roles in cluster formations.
With the projected MDCRHB model (p-MDCRHB), we are able to explore various exotic nuclear shapes.One direct application involves searching for possible α-clustering structures in light nuclei.As the first step toward this direction,in this work we only consider the AMP and PP methods.The particle number projection method and GCM also play essential roles in some circumstances and will be considered in future works.In section 2, we present the theoretical framework of the p-MDCRHB model.In section 3, we present the numerical check and the results for the α-conjugate nucleus12C.We summarize this work in section 4.
2.Theoretical Framework
CDFTs solve the nuclear many-body problems within the framework of the density functional theories.We design a general energy density functional E[ρ(r)], where ρ(r) is the intrinsic nucleon densities, then the ground state energy and densities are given by the variational principle δE/δρ=0.In most CDFTs this framework is formally equivalent to a mean-field approximation for an effective Lagrangian, in which the nucleons are Dirac fermions interacting indirectly via meson exchange (ME) or directly through zero-range point-coupling interactions [97, 98].To give the correct saturation properties of the symmetric nuclear matter,the nonlinear self-coupling terms[99–101]or the density dependence of the coupling constants [102, 103] were introduced and applied extensively.Accordingly, the framework of CDFT can be formulated using four representations:effective interactions with ME,or point-coupling(PC)combined with nonlinear self-coupling (NL) or density dependence of coupling constants (DD).In MDCCDFT we implemented all four possibilities.In this work,we illustrate the formalism of the projected MDCRHB model using the density-dependent point-coupling interaction DD-PC1[104].The formalisms for other parameters are similar and omitted for brevity.
2.1.Relativistic Hartree–Bogoliubov model
In this section we briefly introduce the theoretical framework of the MDCRHB model with density-dependent point-coupling interactions.We start with the effective Lagrangian



with x=ρ/ρsat, where ρsatdenotes the saturation density of the symmetric nuclear matter.The constants ai, biand ciare parameters fitted to the experiments.
The pairing correlations are included with the Bogoliubov transformation.According to the mean-field approximation, we take the Bogoliubov vacuum as the trial wave function and solve the variational problem to find the ground state.To prevent the system from collapsing to the negative energy Dirac sea, we apply the ‘no-sea’ approximation, i.e.only the positive energy states are kept when calculating the densities and currents.The resulting RHB equation [58, 105] in coordinate space is
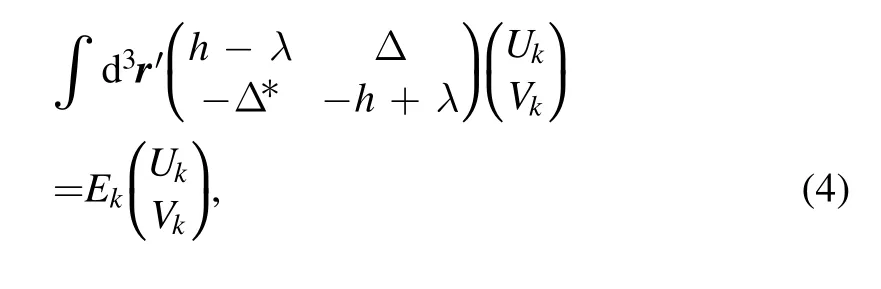

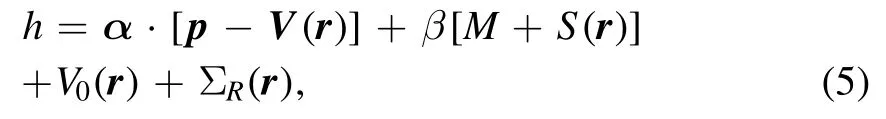
where the scalar potential S(r),vector potential Vμ(r)=(V0(r),V(r))and the rearrangement term ΣR(r)are expressed with various nuclear densities and currents,
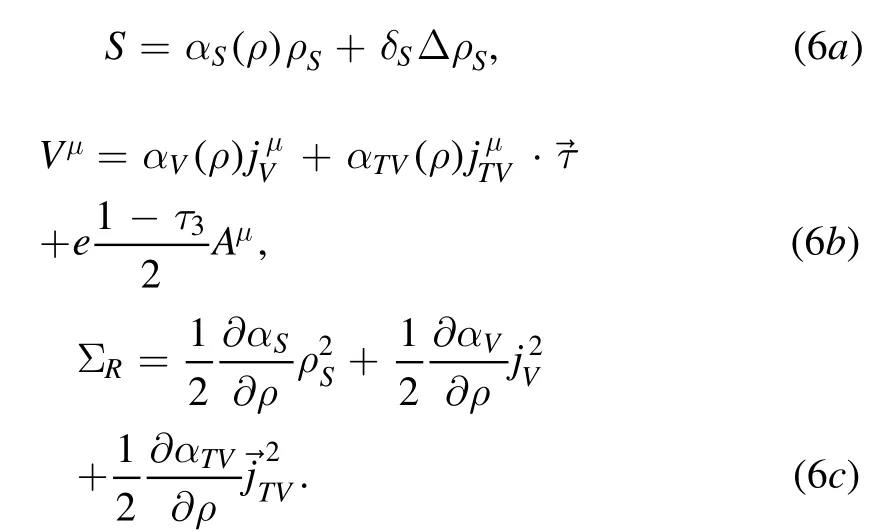
The pairing potential Δ is written as
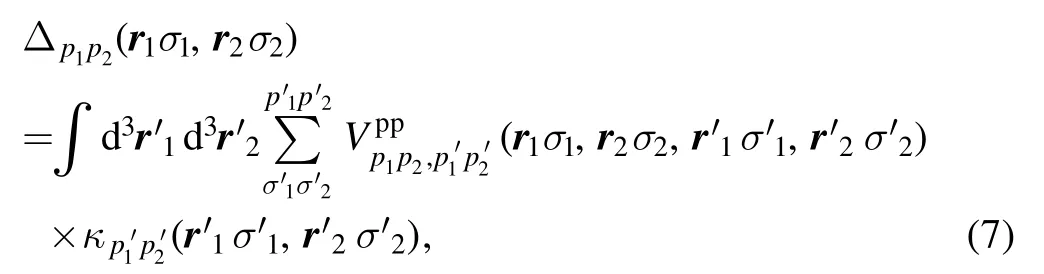
In this work we use a separable pairing force of finite range [107, 108]
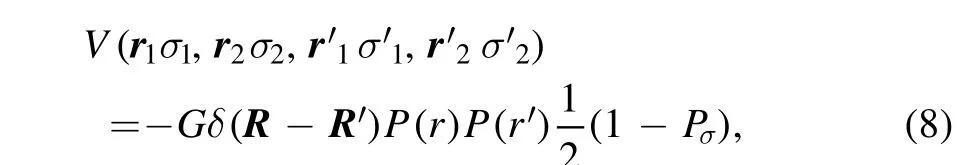
where G is the pairing strength, (1 −Pσ)/2 is the projector onto the total spin S=0, R=(r1+r2)/2 and r=r1−r2are the center of mass coordinate and relative coordinate,respectively.Here, P(r) is a normalized Gaussian functionP(r) =(4πa2)−32exp (−r2/(4a2)), where a is an adjustable parameter specifying the range of the pairing force.The details for calculating the pairing tensor and pairing potential in the axially deformed harmonic oscillator(ADHO) basis can be found in [80].In this illustrative work we fix the pairing strength to G=1.1G0with G0=728.0 MeV·fm3and the range to a=0.644 fm, in which G0and a are determined by fitting to the pairing gap in the nuclear matter [107, 109].
The RHB equation (4) can be solved self-consistently starting from a properly chosen initial state.The resulting minima represent the ground state or the shape isomers.To obtain the PESs, E(β), we use a modified linear constraint method [33].The Routhian with deformation constraints reads

where EMFis the energy functional obtained with the Lagrangian (2) and the pairing force (8).The variable Cλμvaries during the iteration.βλμis the nuclear deformation
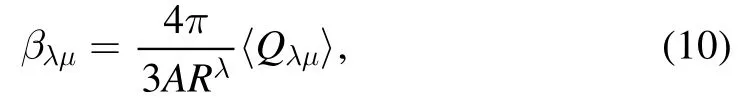
where R=1.2A1/3fm is the approximate nuclear radius, A is the number of nucleons and Qλμ=rλYλμ(Ω),where Yλμis the spherical harmonics, is the multipole moment operator.
2.2.Axially symmetric harmonic oscillator basis
In the MDCRHB model, we solve the RHB equation (4) by expanding the spinor wave functions Uk(rσ)and Vk(rσ)in an ADHO basis [33, 80, 110],

where Φα(rσ)is the basis wave function generated by solving the Schrödinger equation with an ADHO potential.Here, we impose the V4symmetry, which means that the densities and potentials are invariant under the mirror reflections
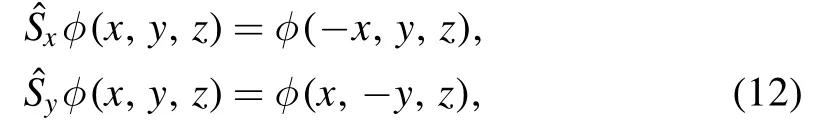
where φ represents any scalar field or spatial distribution in the theory.It immediately follows that the rotationaround the z-axis by π is also a symmetry operation.
In the ADHO basis,the reflection asymmetric shapes can be included by mixing the basis states with different parities.While the axially deformed shapes preserve the z-axis AMP K,the triaxial shapes mix different K blocks and we need to calculate the corresponding mixing matrix elements.In this case,we expand the densities and potentials in terms of the Fourier series of the azimuthal coordinate φ in cylindrical coordinates.Under the restriction of the V4symmetry,the expansion for any field f writes The ADHO basis is also eigenfunctions of the simplex operatorwith eigenvalues S=±1.The basis with S=−1 can be calculated with a time-reversal operation on those with S=1.For a system with time-reversal symmetry, the single particle energy levels have Kramer’s degeneracy and we only need to diagonalize the Hamiltonian in the S=1 subspace.
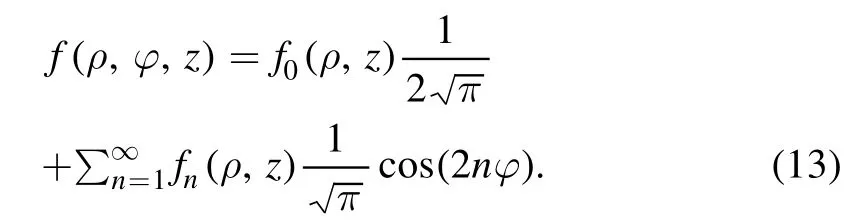
In mean-field calculations we need to calculate the potentials on a cylindrical lattice.The number of mesh points in the z- and ρ- directions are nz=24 and nρ=12, respectively.In MDCCDFT,the triaxial deformation is included by the Fourier transformation given in equation(13).Choosing z as the principal axis, only the n=0 Fourier component survives in the axially symmetric case, which simplifies the calculation, regardless of φ.A triangular deformed system lying on the x-z plane is not axially symmetric about the intrinsic z-axis.In such a system, n>1 components in the Fourier transformation need to be taken into account.Due to the V4symmetry restriction, we only need to calculate the components with even n in the Fourier transformation.The V4symmetry can simplify the calculation into 1/4 of the full space with respect to φ and we choose the number of points for the φ integral as nφ=12 for 0<φ<π/2.
2.3.Angular momentum and parity projections
The AMP operator for a general wave function breaking both the axial symmetry and reflection symmetry can be written as

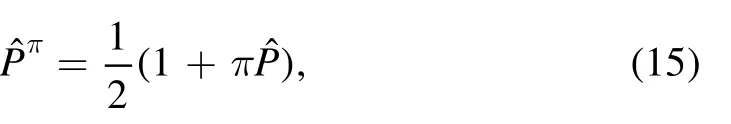
whereis the spatial reflection operation and π=±1 is the parity.
Withand, we can project out states with good angular momentum I, M and parity π from an RHB meanfield wave function |Φ〉,
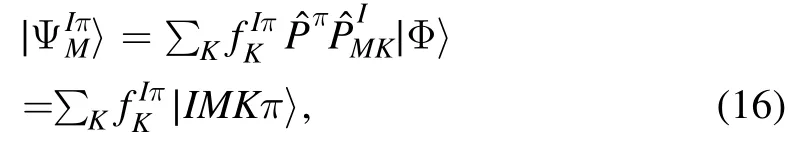
whereare some undetermined constants.Taking equation (16) as the trial wave function and solving the variational problem against the variables,we end up with the Hill–Wheeler–-Griffin equation [74]

where the Hamiltonian kernelH and the norm kernel N are defined as

Note that the expressions of the kernels are derived by considering the V4symmetry.By discretizing the group space,the problem turns to the calculation of the norm overlap n(Ω)and the Hamiltonian overlap h(Ω) as functions of the Euler angle Ω,
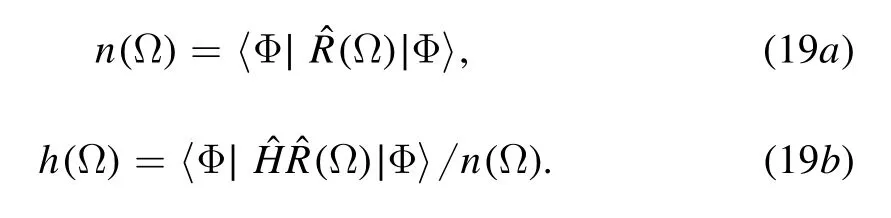
We adopt the method introduced in [94] to calculate the overlaps in the ADHO basis using the generalized Wick’s theorem.
We follow the standard way of solving the Hill–Wheeler–Griffin equation (17),as discussed in[74].The first step is to diagonalize the norm kernel

The normalized vectors can be used to build the orthonormalized basis
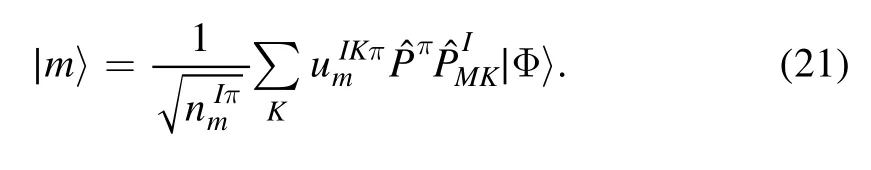
Eigenvectors with small eigenvaluesmay induce numerical instabilities.To solve this problem, we introduce a cutoff χ=10−3and only consider eigenstates with eigenvalues>χ.In the othornormalized basis |m〉 the Hill–Wheeler–Griffin equation becomes a standard eigenvalue problem,

The eigen energiescan be solved by matrix diagonalization and the wave function componentscan be obtained from the corresponding eigenvectors
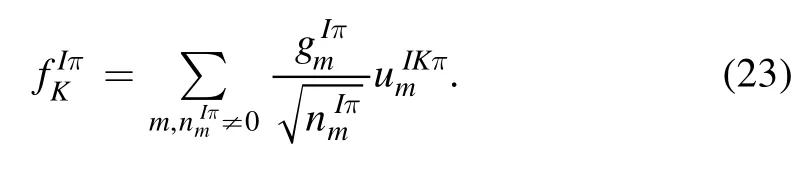
With the projected wave functions, the reduced transition probabilities B(Eλ) from the Jistate to the Jfstate writes
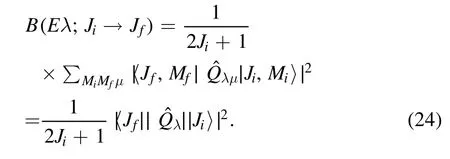
The reduced matrix element has the following expression

where
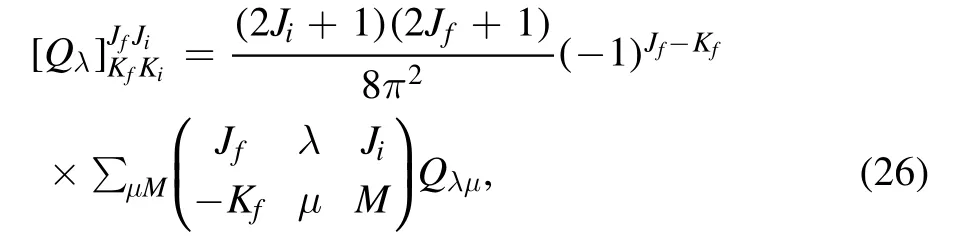
in which
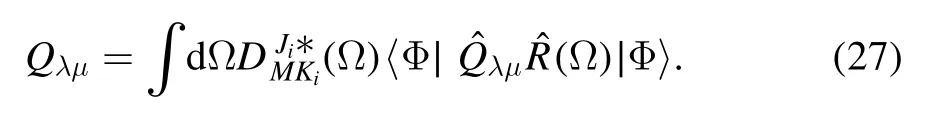
3.Results and discussion
In this section,we apply the p-MDCRHB model to study the low-lying excitations of the nucleus12C, which is a typical nucleus with possible α clustering structures.Among the proposed clustering states,the second 0+state of12C,namely the Hoyle state, is the most interesting because it plays a crucial role in the stellar nuclear synthesis [111].The Hoyle state is a resonance consisting of three interacting α clusters lying above the three-α breakup threshold [112].The energy and width of this resonance play an essential role in synthesizing three αʼs into12C in the main sequence stars.The abundance of the carbon elements would be insufficient for supporting life in our universe if the Hoyle state has a different energy or does not exist at all.Furthermore, several recent studies of the ground state band indicate that the 3-α structure may already appear in the ground state of12C[53, 113].A 5−state was measured in the ground state band[54], providing evidence of a triangular D3hsymmetry.
In the MDCRHB model and its extensions, the system respects the mirror symmetries about the x-z and y-z planes.One interesting case in which these models specialize in is the clustering structure in the light α-conjugate nuclei.Here, the α clusters can form various molecular-like structures and the possible shapes include rod,triangle,tetrahedron,octahedron,etc.Most of these shapes cannot be described by a conventional multipole expansion method that only includes either triaxial or octupole deformations.Further,the structure might be different for the ground state and the excited state,a meanfield description is too simplified and we must take into account the symmetry restorations with projection techniques.
In this section,we apply the p-MDCRHB model to study the ground state and low-lying excitations of a12C nucleus with an intrinsic triangular shape.To generate such a configuration,we define a triangular deformation constraint in the mean-field calculations.In analogy with the usual multipole deformation constraint equation (10), we use the ansatz
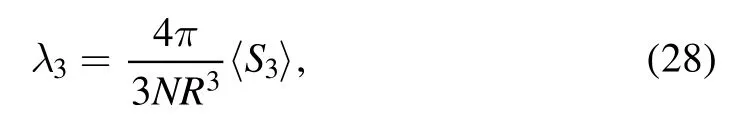
where the ‘triangular moment operator’ is defined as
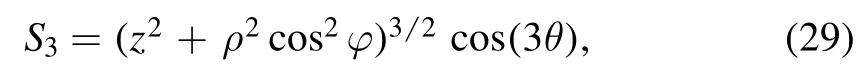
where ρ, φ and z are the cylindrical coordinates andθis the polar angle on the x-z plane.We can verify that equation(29)has the desired symmetry.If rotated around the y-axis, the operator S3has a period 2π/3 and the maxima point to the directions along which the nucleus is stretched.The parameter λ3is the counterpart of the multipole deformation parameters βλμ.When constrained to a large λ3,the operator S3elongates the nucleus in the directions θ=0, 2π/3, 4π/3 and compresses it in other directions.The resulting shape would be a regular triangle with three4He at the vertices.In the MDCRHB model, the triangular constraint can be implemented in exactly the same way with the multipole moment constraint.In figure 1 we show the density profiles of12C constrained to λ3=0.8.We present the contours in all three coordinate planes x=0,y=0,z=0 and a 3D isosurface.The densities are consistent with what we expect from the structure of the triangular moment constraint.The energetically preferred directions are distributed evenly in the x-z plane.With much stronger constraining potential, individual α clusters can form and be squeezed out of the nucleus.
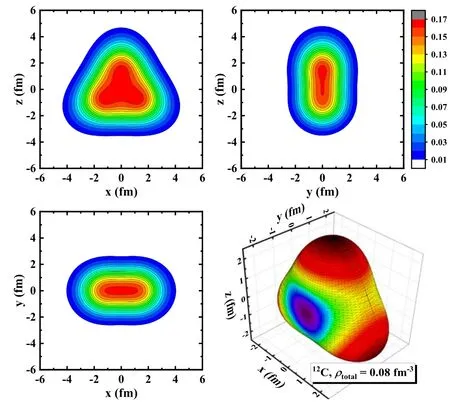
Figure 1.Density profiles of 12C constrained for λ3=0.8.The contour plots display the total density ρtotal in the x-z, y-z and x-y planes(top left,top right and bottom left,respectively).The 3D plot(bottom right) shows the isosurface of ρtotal=0.08 fm−3.
In mean-field calculations, the Dirac equation is solved by expanding the wave functions in an ADHO basis with a major shell truncation Nf.For Dirac spinors we use Nfshells to expand the large component and Nf+1 shells to expand the small component to remove the spurious states.Firstly,we examine the convergence of the mean-field results against the basis truncation Nf.In figure 2 we present the PESs of12C calculated with the triangular constraint using different values of Nf.We found that all energy minima locate at λ3=0 corresponding to a spherical shape.There is no explicit triangular correlation in the mean-field level.As Nfincreases,differences between adjacent curves become smaller, signifying a clear convergence pattern.At the ground state λ3=0, the calculated binding energy already converges at Nf=8, with the truncation error smaller than 0.1 MeV estimated by comparing to the result at Nf=12.For a larger λ3,the mean-field potential assumes a triangular shape, differing from that of the harmonic oscillator basis.In this case we observe a slower convergence.For example, the mean-field energies for Nf=10 and Nf=12 differ by about 1 MeV for λ3≈3.0.Nevertheless,the qualitative behaviour of the PES is not changed when Nfis large enough.Concerning the big computational cost of the 3D AMP, in this illustrative work we use Nf=8 in all of the following calculations.For more realistic calculations we need to either employ a triangular harmonic oscillator basis or increase Nfuntil all truncation errors are smaller than the desired precision.

Figure 2.The energy of 12C as functions of the triangular shape parameter λ3 calculated with different basis truncations in the MDCRHB model.The squares, circles, up triangles and down triangles denote the results obtained with major shell truncation Nf=6, 8, 10 and 12, respectively.The center of mass correction to the binding energy is not included.
For angular momentum and parity projections, the Hamiltonian kernel equation (18a) and the norm kernel equation (18b) are calculated by integrating over the SO(3)group space parameterized by the Euler angles (α, β, γ).These integrals are performed numerically by the Gauss–Legendre integral with numbers of mesh points(nα,nβ,nγ)in the α, β and γ directions, respectively.As most of the computational cost comes from the calculation of the Hamiltonian overlap and norm overlap for each Euler angle,it is desirable to reduce the total number of integral mesh points for a given precision.Here, we make a convergence check against the number of mesh points in the group space.In figure 3, we show the projected energies as functions of nα,nβand nγ.On the left panel, we set nβ=8 and study the projected energies for 6 ≤nα=nγ≤14, where EJπdenotes the energy of the lowest∣Jπ〉 state with the corresponding Euler angle mesh size,andrepresents the energy with the largest mesh size.We see that the influence of nαand nγon the projected energies for J<6 is less than 10 keV, which is negligible compared with the excitation energies of the order of MeV.In contrast,the right panel shows that the number nβhas a rather large influence on the projected energies.All projected energies up to 6+achieve relative precisions less than 10−6when nβ≥10.In this work, we choose the mesh sizes nα=nγ=12 and nβ=14, with which the numerical integral in the group space can be evaluated rather precisely for J ≤6.
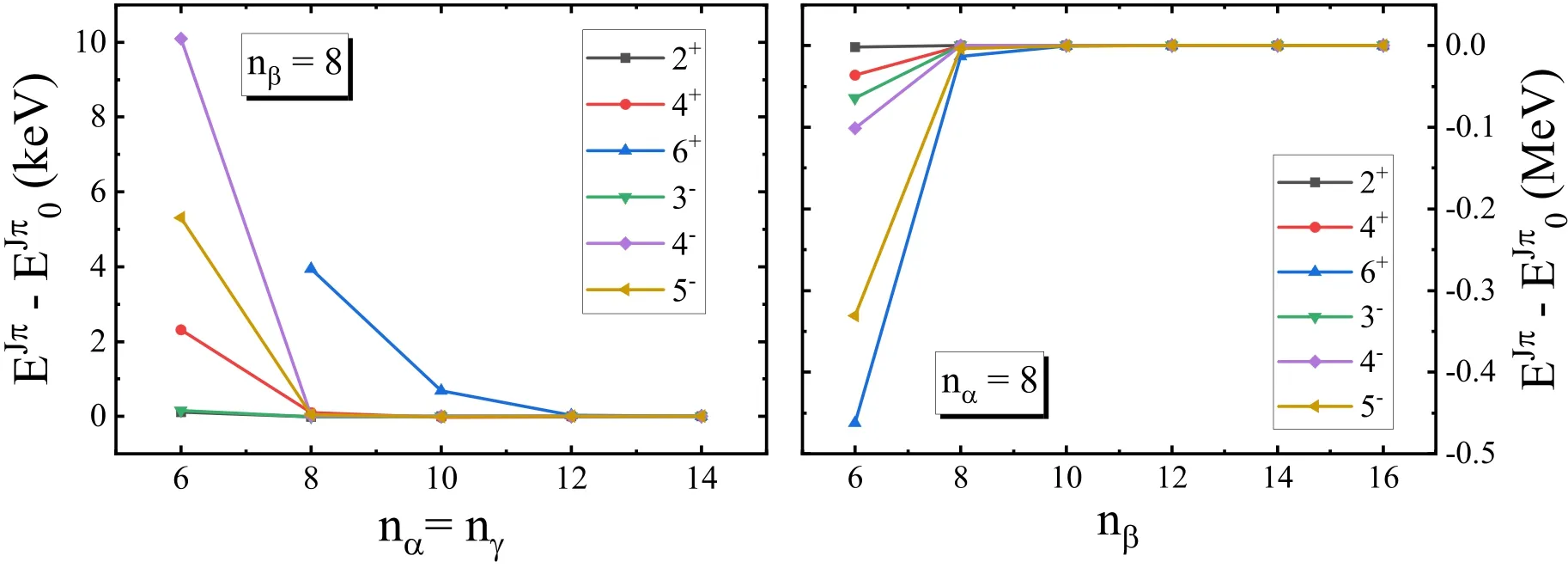
Figure 3.The projected energies of 12C calculated with different mesh sizes for the SO(3) group integral.For each curve, the energies are relative to the corresponding converged values calculated at large mesh sizes.All calculations are performed with a mean-field wave function constrained to λ3=1.2.Here,nα,nβ and nγ are the number of mesh points for integrating the Euler angles α,β and γ,respectively.Squares, circles, up triangles, down triangles, diamonds and left triangles denote results projected to Jπ=2+, 4+, 6+, 3−, 4−, 5−,respectively.
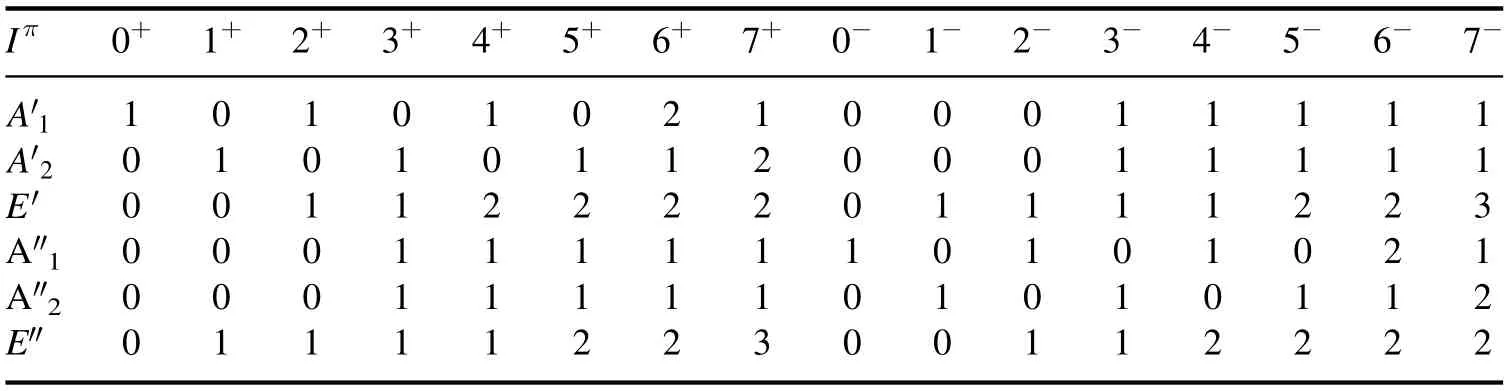
Table 1.The decomposition of the irreps of the O(3) group with quantum numbers Iπ into irreps of the D3h group.In each column the numbers are the degeneracies.
The constraint equation (29) produces a triangular shape with the 3-fold axis pointing along the y-axis and one of the 2-fold axes pointing along the z-axis.For AMP we rotate the mean-field wave function to Euler angles(α,β,γ)and calculate its overlap with the original wave function.These norm overlaps should exhibit periodicity if the rotations are about the symmetry axes of the intrinsic shape, which can be examined numerically.In figure 4 we show the norm overlaps for different Euler angles.All results are calculated with a mean-field wave function constrained to λ3=1.2.In the left panels we set β=γ=0 and rotate the nucleus around the z-axis by increasing α from 0°to 360°.As the z-axis is a 2-fold axis of the triangle,we found a period of 180° for both the norm overlap and Hamiltonian overlap.In the right panels we set α=γ=0;then variation of β corresponds to a rotation around the y-axis.In this case we observe a period of 120° for both overlaps, which is consistent with the fact that the y-axis is a 3-fold axis of the triangle.In all subplots, the overlaps return to their original values at α,β,γ=0 after rotating by the corresponding period.This is the direct consequence of the invariance of the nuclear shape under these symmetry operations.

Figure 4.The norm and Hamiltonian overlaps of 12C as functions of the Euler angles α and β, calculated with a mean-field wave function constrained to λ3=1.2.β=γ=0 on the left panels and α=γ=0 on the right panels.

For any state of the triangular rotor with quantum numbers Iπ, the wave function transforms under the corresponding irrep of the O(3)group.If we rotate the rotor with an element of the D3hgroup in the intrinsic frame, nothing is actually changed;thus the wave functions should be scalars for these rotations.In the language of the group theory,the allowed states all belong to theirrep of the intrinsic D3hgroup.If an angular momentum and parity combination Iπdoes not contain anyrrep, it should not appear in the spectrum.In other words,the Iπstates with non-zero entries in the first row of table 1 are all states allowed by the symmetry analysis.In summary, the lowest energy levels of a triangular rigid rotor should be Iπ=0+, 2+,3−,4+,4−,5−,6+,6−,…Other angular momentum and parity combinations should be consequences of the intrinsic excitations.
On the one hand, the group theory analysis is strict and can be generalized to any other intrinsic shapes.For example,we can predict the low-lying states of a tetrahedral rotor and compare the results with that of the16O nucleus, which was predicted to exhibit a four-α cluster structure.On the other hand, there are also less abstract ways of understanding the essentiality of the nuclear rotational spectrum.For a triangular rotor, a stable rotation can only occur around its symmetry axes.The wave function for angular momentum I isψ(φ) = exp (iIφ), where φ is the rotational angle.For an nfold axis we must have ψ(φ+2π/n)=ψ(φ);thus,among all integer values of I, only integer multiples of n are allowed.For example, the rotations about a 2-fold axis generate angular momenta I=0,2,4,6,…,while the rotations about a 3-fold axis give the angular momenta I=0, 3, 6, … Further,the parity of the rotational wave function can be determined byπ= (− 1)I.The total rotational energy of a triangular rotor is the sum of that around the 2-fold and 3-fold axes.If there is no rotation around the 3-fold axis, we have the spectrum Iπ=0+, 2+, 4+, 6+, … If there is one unit of quantized angular momentum around the third axis, we have the states Iπ=3−, 4−, 5−, 6−, … Here, the states 4−and 5−can be understood as a rotation around the axis in between the 2-fold axis and the 3-fold axis,which is already a complex motion in the classical level.
Next, we turn to the projected PES.We first generate mean-field configurations with λ3varying from 0.0 to 5.0.The results describe the disintegration of12C into three α clusters.In figure 5 we show the projected energies as well as mean-field energies for all λ3in this interval with a step size Δλ3=0.2.Here,we only show the lowest energy levels with Iπ=0+, 2+, 3−, 4±and 5−.The mean-field PES gives a ground state at the spherical shape λ3=0.The energy increases quickly as three αʼs are separated.For λ3=1.0 the deformation energy is more than 5 MeV, preventing the dissociation of the nucleus.By projecting out the spurious rotational energies, we see that the PES for the 0+state is quite different from the mean-field PES.The 0+PES is lower than the mean-field PES and becomes very flat for λ3<2.0.We find a minimum at λ3=1.2,which is very shallow in that the energy at λ3=0 is only about 1 MeV higher.In the insets of figure 5 we show the density profiles from the mean-field calculations at λ3=1.2 and λ3=3.8.The first inset corresponds to the ground state identified with the 0+PES.Although, at this point there is no emerging clustering structure, we can see a clear triangular shape from the total densities.At λ3=3.8 the deformation is so strong that the clustering structure is very pronounced.Theoretically, for extremely large λ3,the12C nucleus would break up into three α particles and the energy should converge to three times the4He binding energy.However,for such light nuclei we might need a very large center of mass correction and the mean-field model might not be a good approximation.Even though there are still a lot of difficulties, the extremely large λ3deformation still deserves some further investigations.This three-α disintegration can be viewed as an inverse reaction of the famous 3α →12C reaction and may be related to the Hoyle state.Whether the mean-field model is adequate for describing such a process and what is lacking is thus an interesting topic.Although in recent years ab initio calculations have been more popular for studying clustering structures, meanfield models have clear physical pictures and have proven successful on this topic.The p-MDCRHB model we presented here can describe various α cluster configurations and can serve as a starting point for beyond-mean-field calculations in this direction.

Figure 5.The mean-field and the projected potential energies of 12C versus the triangular deformation λ3.The squares, circles, down triangles,up triangles,diamonds and left triangles represent Iπ=0+,2+, 3−, 4+, 4−and 5−, respectively.The mean-field energies are displayed as a black solid line.The insets show the mean-field density profiles at λ3=1.2 and 3.8.
The PESs for higher angular momenta tell us how the α clusters move about the rotational axes.At λ3=0 the system is spherical and there is no rotation.For larger λ3,the 2+and 4+states describe rotations around the 2-fold axes, and the corresponding PESs have mimina at relatively small λ3.The 3−and 4−states contain rotations around the 3-fold axis;thus, the centrifugal force prefers a larger λ3, which also means a larger moment of inertia.
The energy spectra of12C at large λ3can be understood by comparing them to the spectra of a triangular rigid rotor discussed above.By taking such a rotor with equal masses on the three vertices, we can compute the moment of inertia M along every principle axis.For the orientation shown in figure 1, the principle axes are simply the three coordinate axes x, y and z.It is straightforward to prove that 2xM =2zM =My=M.By only considering rotations about the center of mass, we can write the Hamiltonian as
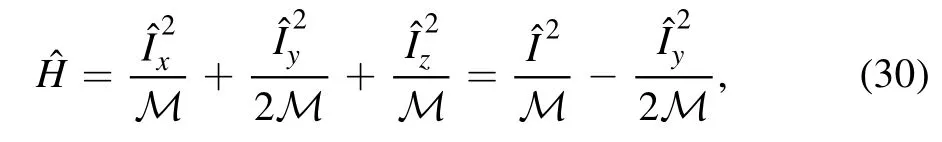

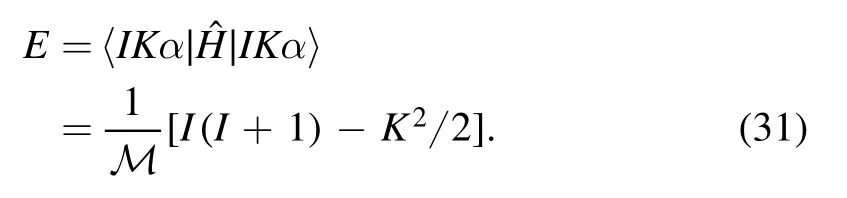
The spatial reflection P combined with a rotation around the 3-fold axis by 180° resets the system.The operator P produces a factor of parity π and the rotation gives an additional phase of (− 1)K; thus we haveπ= (−1)Kfor all physically allowed states.
The energy spectrum of equation (31) can be classified according to the quantum number K.For K=0 we have the ground state band 0+, 2+, 4+, ..., with positive parity.For K=3 we have a negative parity band 3−, 4−, 5−, ...The excitation energies relative to the 0+state are

up to an overall multiplicative factor.One important feature of this spectrum is that the 4+energy is higher than the 4−energy.The reason for this is that the 4+state is a pure rotation around the 2-fold axes, while the 4−state contains rotations around the 3-fold axis.The moment of inertia for the latter rotation is relatively larger.However,in figure 5 we see that the 4+state is much lower than 3−and 4−for small λ3;only for extremely large λ3can the projected energies be explained by the rigid rotor model.The reason is twofold.First, the relationMy=2zM used to derive the rigid rotor spectrum is only approximately satisfied for large deformations where the masses of α clusters are concentrated at the vertices.For small λ3we have a triangular density distribution without clustering and the moments of inertia along different axis are not so different.Second, the angular momentum andparity projections capture the full quantum mechanical elements.The impact of the intrinsic states is reflected by the calculated norm kernel and Hamiltonian kernel.Only for large λ3can we omit the intrinsic structures and use the Gaussian overlap approximation to treat the α clusters as point particles.
Table 2.Reduced E2 transition probabilities from states to states and the corresponding excitation energies of 12C.The calculation is made for λ3=1.2, corresponding to the energy minimum of the 0+ PES shown in figure 5.The experimental B(E2) value is taken from [117].

Table 2.Reduced E2 transition probabilities from states to states and the corresponding excitation energies of 12C.The calculation is made for λ3=1.2, corresponding to the energy minimum of the 0+ PES shown in figure 5.The experimental B(E2) value is taken from [117].
Iiπ ExiTh (MeV) Exi Expt(MeV) Ifπ ExfTh (MeV) B E2 Th() (e2 fm4) B E2 Expt() (e2 fm4)2+ 1.951 4.440 0+ 0.000 9.72 7.6±0.4 [117]4+ 9.015 14.079 2+ 1.951 16.28 4− 15.253 3− 12.864 20.95 5− 19.915 3− 12.864 6.78 4− 15.253 18.90 61+ 26.734 4+ 9.015 26.04 6− 25.131 4− 15.253 13.38 5− 19.915 15.01
Table 3.Reduced E3 transition probabilities from states to states Ifπ and the corresponding excitation energies of 12C.The calculation is made for λ3=1.2, corresponding to the energy minimum of the 0+ PES shown in figure 5.The experimental B(E3) value is taken from [117].

Table 3.Reduced E3 transition probabilities from states to states Ifπ and the corresponding excitation energies of 12C.The calculation is made for λ3=1.2, corresponding to the energy minimum of the 0+ PES shown in figure 5.The experimental B(E3) value is taken from [117].
Iiπ ExiTh(MeV) Exi Expt(MeV) Ifπ ExfTh(MeV) B E3 Th() (e3 fm6) B E3 Expt() (e3 fm6)3− 12.864 9.641 0+ 0.000 145.81 103±17 [117]2+ 1.951 260.25 4+ 9.015 53.53 4− 15.253 13.35 2+ 1.951 268.69 4+ 9.015 198.55 5− 19.915 22.4(2) 2+ 1.951 96.28 4+ 9.015 318.35 61+ 26.734 4− 15.253 33.95 5− 19.915 129.86 6− 25.131 250.19 62+ 27.234 3− 12.864 480.28 4− 15.253 219.26 5− 19.915 90.68 6− 25.131 30.99 6− 25.131 4+ 9.015 274.90
In table 2 and table 3 we compare the low-lying spectrum and reduced transition probabilities B(E2) and B(E3) of12C with the experiments.The results are calculated by projecting a mean-field state constrained to λ3=1.2,which corresponds to the minimum of the 0+PES in Fig 5.The experimental values are well reproduced at this level of approximations.These results can be improved from various aspects.First, as the PESs are soft at small λ3, in figure 5 we see that the λ3value minimizing the projected energy has a strong dependence on Iπ,which should be considered when calculating the energy spectrum.Second,the soft PESs suggest we introduce the GCM to mix different deformations.Lastly, other configurations like the rod shape might also play an important role in the low-lying excitations and should be considered when building the low-lying states with good quantum numbers.
In [52], the α arrangement in12C is assumed to be an equilateral triangle.In [118], the author performed calculations using the orthogonality condition model and the shallow potential model, and obtained different configurations for each model.Due to insufficient experimental data, whether the intrinsic configuration of the ground state of12C is a regular triangle remains an open question [118].It is necessary to explore this point by performing multidimensional constrained calculations that include all important shape configurations.In figure 6 we show the projected 0+PES of12C with respect to the deformation parameters β20and λ3.Here, we constrain λ3from 0.0 to 3.0 with a step size Δλ3=0.2, and constrain β20from −0.2 to 1.0 with a step size Δβ20=0.1.The projected energies are much lower than the mean-field energies for non-zero deformations.The rotational energy correction,defined as the difference between the 0+energy and the mean-field energy, plays a key role in determining the ground state configurations.On the 0+PES,we found two energy minima.The lowest one locates at λ3=0.8 and β20=0.6, corresponding to an isosceles acute triangular shape, while the shape isomer at λ3=1.2 and β20=−0.1 corresponds to an isosceles obtuse triangular shape.

Figure 6.The 2D PES of 12C projected to the 0+ state.The λ3 and β20 constraints are imposed with 0<λ3<3.0, Δλ3=0.2 and −0.2<β20<1.0; Δβ20=0.1.
4.Summary
We have developed a p-MDCRHB model.In this model, the shape of the system is only restricted as mirror reflection symmetric about the x-z and y-z planes.In the mean-field calculation, the RHB equation is solved in the ADHO basis.The parity and angular momentum projections are performed to restore the intrinsic symmetries.
This model is well suited for exploring exotic shapes like triangles and tetrahedrons found in both the nuclear ground state and low-lying excited states.One important scenario where these shapes play essential roles is nuclear clustering.The most important stellar nuclear reactions, such as the production of carbon and oxygen, depend heavily on the clustering structures of the reactant.In this work we benchmark the p-MDCRHB model by studying the clustering states in12C.We define a triangular moment constraint and study the corresponding triangular deformation λ3.This constraint generates a clustering state with three α clusters arranged on the vertices of a regular triangle.We found that with the growth of λ3,the spectra approach that of a regular triangular rigid rotor.This was explained by symmetry analysis and the rigid rotor Hamiltonian.We also performed 2D constrained calculations of12C.Two minima are found on the projected 0+PES.The softness of the PESs indicates that the configuration mixing GCM calculation is needed for a deeper understanding of the structure of12C and the related nuclear reactions occurring in the stellar environment.
Acknowledgments
Helpful discussions with Xiang-Xiang Sun and Yu-Ting Rong are gratefully acknowledged.We thank Xiang-Xiang Sun and Shan-Gui Zhou for reading the manuscript and valuable suggestions.This work has been supported by NSAF(Grant No.U1930403), the National Key R&D Program of China (Grant No.2018YFA0404402), the National Natural Science Foundation of China (Grant No.11 525 524, No.12 070 131 001, No.12 047 503, and No.11 961 141 004),the Key Research Program of Frontier Sciences of Chinese Academy of Sciences(Grant No.QYZDB-SSWSYS013)and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No.XDB34010000 and No.XDPB15).The results described in this paper are obtained on the Highperformance Computing Cluster of ITP-CAS and the ScGrid of the Supercomputing Center, the Computer Network Information Center of the Chinese Academy of Sciences.
Appendix: Calculation of the Rotation Matrix
Since the rotation matrix is naturally written as the Wigner Dfunction with spherical harmonic oscillators, the calculation of the rotation matrix can be simplified by expanding the ADHO basis with the spherical harmonic oscillator (SHO)basis.
An ADHO basis∣α〉with quantum numbers {nz, nρ, ml,ms} reads

with


The SHO basis function reads
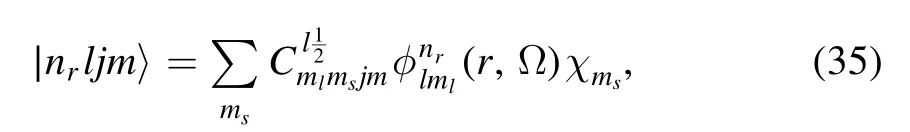
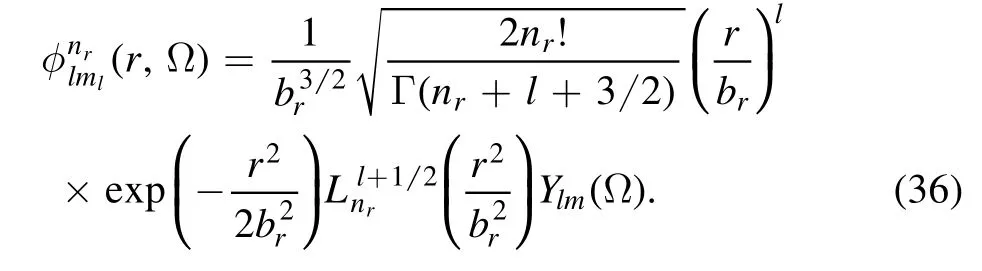
The transformation matrix can be written as

From equations (34) and (36), one can calculate the transformation matrix element, which has also been given in[119]
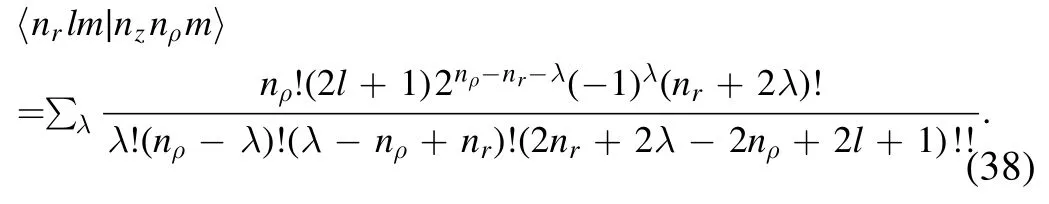
Thus, one obtains the relation between ADHO and SHO bases,

The time-reversal states of the SHO basis are obtained by applying the time-reversal operator

The rotation matrix in the ADHO basis is calculated as

By applying the properties of the Wigner D-function, one finds the relation
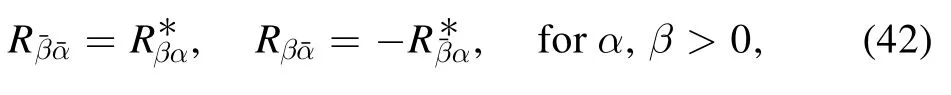
that means only half of the R matrix elements are needed in equation (41), while the other half can be calculated directly from the relation (42).
杂志排行
Communications in Theoretical Physics的其它文章
- Impact of Joule heating and multiple slips on a Maxwell nanofluid flow past a slendering surface
- Generating a dynamical M2 brane from super-gravitons in a pp-wave background
- Uncertainty relation of successive measurements based on Wigner–Yanase skew information
- Quantum uncertainty relations of Tsallis relative α entropy coherence based on MUBs
- Performance of passive decoy-state quantum key distribution with mismatched local detectors
- Quasi-exactly solvable decatic model description of nuclei near the X(5) critical point
