Hyperonic neutron stars: reconciliation between nuclear properties and NICER and LIGO/VIRGO results

Luiz L Lopes

Centro Federal de Educação Tecnológica de Minas Gerais Campus VIII; CEP 37.022-560,Varginha—MG - Brasil

Abstract Using an extended version of quantum hadrodynamics,I propose a new microscopic equation of state(EoS)that is able to correctly reproduce the main properties of symmetric nuclear matter at the saturation density, as well as produce massive neutron stars and satisfactory results for the radius and the tidal parameter.I show that this EoS can reproduce at least a 2.00 solar mass neutron star,even when hyperons are present.The constraints about the radius of a 2.00 M⊙and the minimum mass that enables a direct Urca effect are also checked.

Keywords: neutron star, nuclear matter, tidal deformability, DU process, hyperons

1.Introduction

Our knowledge of nuclear physics and nuclear astrophysics took a great leap in the last decade.From nuclear mass analysis[1],passing through nuclear resonances[2,3],and heavy ion collisions (HIC) [4], we are able to constrain six parameters of the symmetric nuclear matter at the saturation point:the saturation density itself (n0), the effective nucleon massthe incompressibility (K), the symmetry energy(S0)and its slope(L),as well as the binding energy per baryon(B/A) [5].

On the other hand, quiescent analyses [6] and Shapiro delay measurements [7] constrain the radius of the canonical star,as well as the minimum mass that a microscopic equation of state(EoS)needs to reproduce to be considered valid.The constraints improved in recent years with results for the NICER x-ray telescope[8],and also from the analyses of the so-called GW170817 event, detected by the LIGO/VIRGO gravitational wave observatories [9].Moreover, the newly opened gravitational waves window gives us an additional constraint: the dimensionless tidal deformation parameter Λ.Another recent constraint is related to how squeezable the neutron stars are.In the past,it was believed that very massive neutron stars should be smaller than less massive ones.However, a very recent study [46] shows that a two solar mass and a canonical mass of 1.4 M⊙have very similar radii.This fact puts an additional constraint on the microscopic EoS.

Nowadays,one of the open issues in nuclear astrophysics is the content of the inner core of massive neutron stars.Because of the Pauli principle, as the number density increases,the Fermi energy of the nucleons exceeds the mass of heavier baryons,and the conversion of some nucleons into hyperons becomes energetically favorable.Among others,two extensive studies about the hyperon threshold [11, 12]show that hyperons are ultimately inevitable.Otherwise, it has been well known for a long time that the hyperon onset softens the EoS.In some cases,this softening of the EoS puts the maximum mass below the observational limits of massive neutron stars.This possible conflict between theory and observation is called the hyperon puzzle.

The hyperon puzzle can be avoided by assuming a very stiff EoS, as in GM1 [13] or NL3 [14], which produce very massive neutron stars, despite the hyperon threshold.However, due to the refinement of the constraint in both nuclear properties and astrophysical observations, these models cannot be considered realistic anymore.Another possibility is the use of strongly repulsive three-body forces,as shown in[15].As the strength of the three-body forces is not yet constrained,this is an open issue.

Table 1.Parameters of the model utilized in this work and their predictions for the symmetric nuclear matter at the saturation density; the phenomenological constraints are taken from [26–29], as well as the recent PREX2 results [30].

In this work, I present a new microscopic EoS via an extended version of the quantum hadrodynamics (QHD)Lagrangian which, besides the traditional non-linear σωρ mesons,also employs the hidden strangeness φ vector meson,which couples only to the hyperons and a non-linear ω −ρ coupling,present in models like the IUFSU [16].Also, to fix the hyperon–meson coupling constant, I use complete symmetry arguments, as presented in [17].

The formalism, the parametrization, and the constraints of symmetric nuclear matter at the saturation point,and supranuclear densities are presented in section 2; the astrophysical results and the astrophysical constraints are presented in section 3; finally, the conclusions are drawn in section 4.

2.Formalism

The non-linear σωρ QHD has the following Lagrangian density [5]:

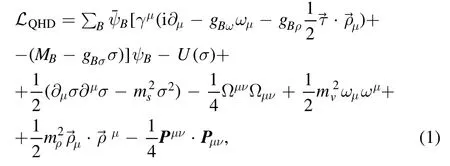
in natural units.The sum in B can only run over the nucleons,or the entire baryon octet;ψBis the baryonic Dirac field.The σ, ωμandare the mesonic fields.Theg′sare the Yukawa coupling constants that simulate the strong interaction, MBis the baryon mass,while ms,mv,and mρare the masses of the σ,ω, and ρ mesons, respectively.The antisymmetric mesonic field strength tensors are given by their usual expressions, as presented in [5].The U(σ) is the self-interaction term introduced in [18] to fix the incompressibility, given by:

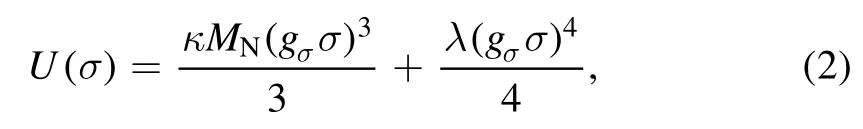
andare the Pauli matrices.Now,besides the traditional nonlinear σωρ QHD, we need to introduce two additional terms.The first is the hidden strangeness φ vector meson, which couples only with the hyperons, and does not affect the properties of symmetric matter:

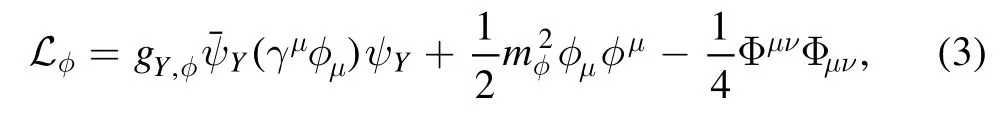
and, as pointed out in [12, 19–21], this vector channel is crucial to obtain massive hyperonic neutron stars.The second is a non-linear ω-ρ coupling meson, as presented in the IUFSU model [16]:

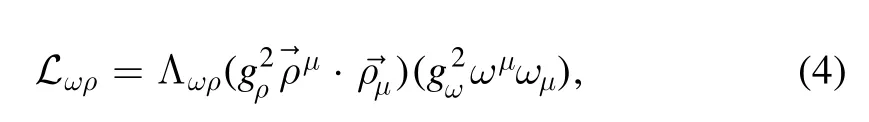
which is necessary to correct the slope of the symmetry energy (L), and has a strong influence on the radii and tidal deformation of the neutron stars [22, 23].

To produce beta-stable matter with zero net charge,I also add leptons as a free Fermi gas.The detailed calculation of the EoS for symmetric nuclear matter, as well as for betastable matter in the QHD formalism is out of the scope of this work, but is well documented and can easily be found in the literature[5,24,25].In the same sense,the calculation of the six nuclear parameters at the saturation densitycan be found in [5, 22] and the references therein.

2.1.Parametrization and nuclear constraints

The parametrization utilized in this work as well as the predictions of this model for the symmetric nuclear matter are presented in table 1.The nuclear constraints at the saturation density are also presented in table 1 and are taken from two extensive review articles, [26, 27].Besides, the masses of the particles are the physical ones.The meson masses are mω=783MeV, mρ=770 MeV, mφ=1020 MeV, mσ= 512 MeV; the baryon octet masses are MN=939 MeV,MΛ=1116 MeV, MΣ=1193 MeV, MΞ=1318 MeV;and the lepton masses are me=0.51 MeV and mμ=105.6 MeV.

As displayed,this new parametrization is able to fulfill all the constraints at the saturation density.Notice also that the new PREX2 results show that the slope is constrained between 106±37 MeV [30].Combined with [27], the slope now lies between 69 and 86.8 MeV.The value L=74 MeV fulfills it.As PREX2 still needs confirmation, I only point it out as a curiosity.Besides the saturation point,there are also a couple of attempts to constrain the pressure of symmetric nuclear matter at supra-nuclear densities.In[31],the pressure from 2 to 4.6 times the saturation density was constrained by HIC analyses.On the other hand, as a result of transiently accreting neutron stars in quiescence, [32] constrain the pressure for densities up to 1.0 fm−3.The main problem is that, for high densities, the region constrained in [32] is broader than the region constrained in[31].To overcome this issue, [26] assumes the region from [31] plus an increase of 20%.Here, I follow this prescription and plot in figure 1 the density-dependent pressure of the presented model together with some well-known relativistic parametrizations.The hatched area in red is the constraint originally presented in[31].The 20% increase is the hatched area in blue.

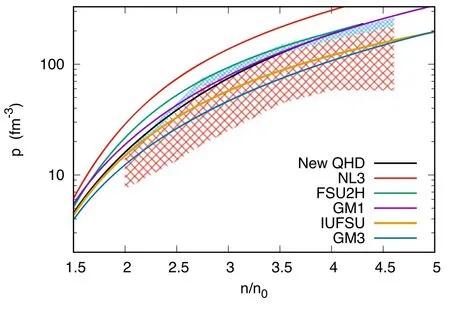
Figure 1.The pressure as a function of the density; the original constraint from [31] (in red), and its value extended by 20% (in blue), to reconcile with the constraint presented in [32].

As can be seen, the model is not flawless.If we assume the original constraint in red, the EoS discussed in this work has an over-pressure, and only fulfills this constraint in the range between 2.52 to 3.43 times the saturation density,which corresponds to 35% of the interval (2–4.6) n0.But, if we assume that the upper limit can be increased by 20%,as in[26], this EoS therefore fulfills the constraint from 2 to 4.20 times the saturation density,which turns out to be 85%of the range.When compared with other parametrizations of the QHD, we see that the presented model presents a higher degree of agreement(85%)in comparison with very stiff EoS,as in NL3 [14] (0%), FSU2H [33] (50%), and GM1 [13](68%),but a lower degree of agreement when compared with soft EoS, as in GM3 [13] and IUFSU [16] (both 100%).

Another two recent constraints at supra-nuclear densities are the symmetry energy at twice the saturation density,S(2n0), and the pressure of the symmetric matter at the same point, p(2n0).The authors in [28] bound S(2n0) in the range between 51±13MeV at 68% confidence level, while [29]fixed p(2n0) between 11.2 MeV fm−3and 38.7 Mev fm−3at the 90%level.These values are also presented in table 1,and the new parametrization also agrees with both.

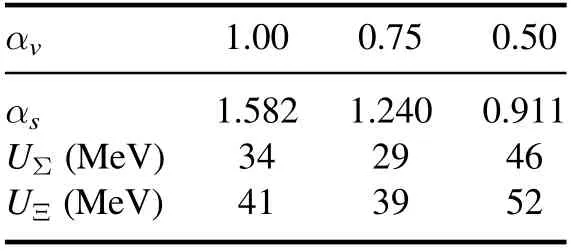
Table 2.The relation of αv with αs to produce UΛ=−28 MeV, as well as the predicted values of UΣ and UΞ.When αv=1.00 we recover the SU(6) symmetry group.

3.Astrophysical results and constraints

Now I turn my attention to the construction of a beta-stable charge-neutral EoS, with and without hyperons.When hyperons are present,it is crucial to define the strength of the hyperon–meson coupling constants.The only well-known parameter is the Λ0hyperon potential depth,UΛ=−28 MeV.We can find several approaches to fix the hyperon–meson coupling constants in the literature, from universal couplings[13], trough to fixed potential depths [12, 34], non-fixed potential depths [17, 21, 35, 36], with and without symmetry group arguments [22,37], and so on.Here,I follow[17]and assume that both vector and scalar mesons are constrained by the SU(3) symmetry group [36, 38].In this case, the relative strength of the hyperon–meson coupling constants are:

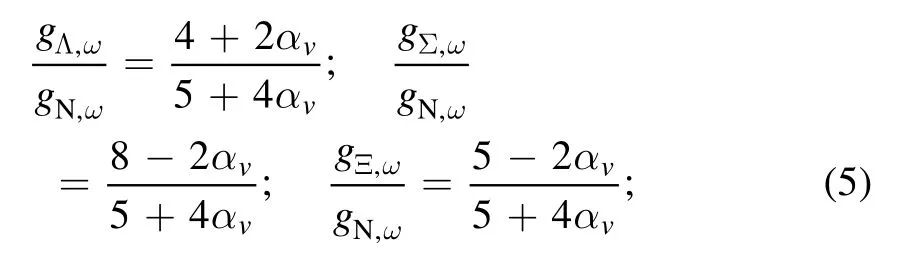
for the ω meson,

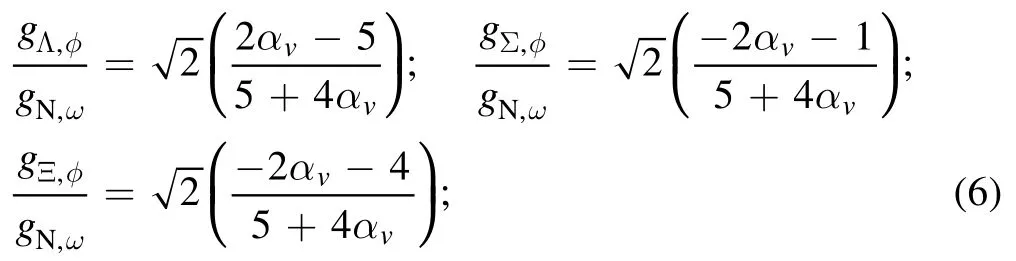
for the φ meson,

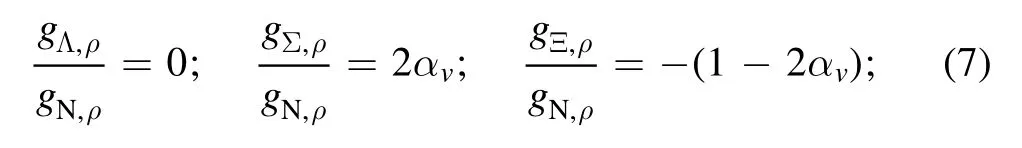
for the ρ meson, and finally:

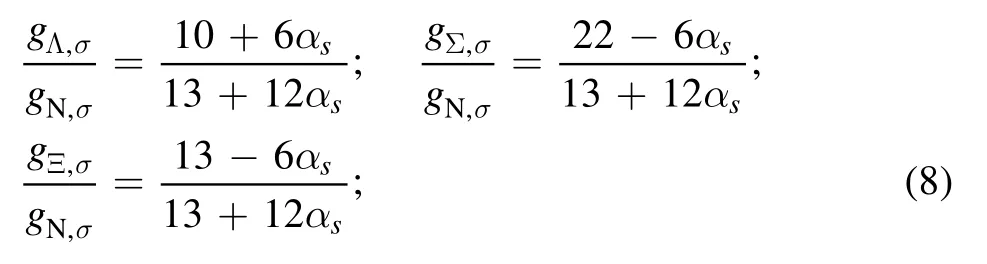
for the σ meson.When we set αv=1, we recover the SU(6)parametrization for the vector mesons[39].Now,to constrain αvto αswe use the well-known Λ0potential depth.Therefore,for a given value of αv, we determine αsto obtain UΛ=-28 MeV.This approach allows us to fix every hyperon–meson coupling constant using only one free parameter: αv.Also, it is worth pointing out that the results from equation (5) to equation (8) are fully model-independent.The results obtained are presented in table 2.The UΣand UΞpotential depths are also calculated.As can be seen, the values for αvequal to 1.00 and 0.75 are more repulsive than the values recently found in ALICE femtoscopic measurements(UΣ=+15 MeV,UΞ=−4 MeV)[40],but still close to what is currently accepted in the literature (±40 MeV) [21].An alternative would be to use the SU(3) symmetry group to fix the vector meson coupling constants while using the potential depth to fix the scalar meson coupling constant, as in[12, 34, 41].However, with this approach, we would need three free parameters instead of just one.

In figure 2, I plot the EoS for beta-stable charge-neutral matter with and without hyperons for different values of αv.I also plot the strangeness fraction fsfor each value of αv, as previous works showed that its value is strongly related to the maximum mass [12, 34].The strangeness fraction is defined as: (fs=∑(ni|si|)/3n) [22].It is also worth pointing out that the sequence of the hyperon threshold for each value of αvis always the same: the first is the Λ0, followed by the Σ−and the Ξ−, except when αv=0.50, where the Σ−is absent.

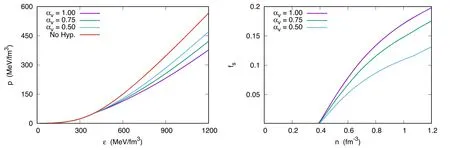
Figure 2.The EoS(left)and the strangeness fraction fs(right)for different values of αv.The higher the value of αv,the higher the value of fs and the softer the EoS.

As expected, there is an inversely proportional relationship between the stiffness of the EoS with the strangeness fraction at high densities.In turn, the strangeness content of the EoS is directly linked to the value of αv.The higher the value of αv,the higher the value of fs.Also,despite the value of αv, hyperons are always present, corroborating the results presented in [11, 12].

The effects of the onset of the strangeness content particles can be seen better by analyzing the square of the speed of sound,as well as the adiabatic index, Γ.They are defined as:

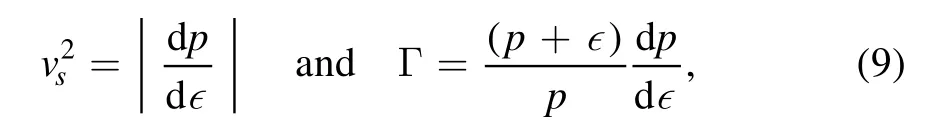
and the results are displayed in figure 3.As can be seen, the onset of the hyperons causes the presence of kinks and peaks in the speed of sound.Therefore,the onset of the Λ0hyperon around 0.4 fm−3can easily be identified.A very important value iscalled the conformal limit[35].In the limit of very high densities n>40n0, pQCD indicates that theshould approach 1/3 from below [42, 43].Nevertheless, in the range of interest for neutron star interiors,n<8n0,we see that the conformal limit is always violated in the proposed parametrization, while the causal limit,is always respected.

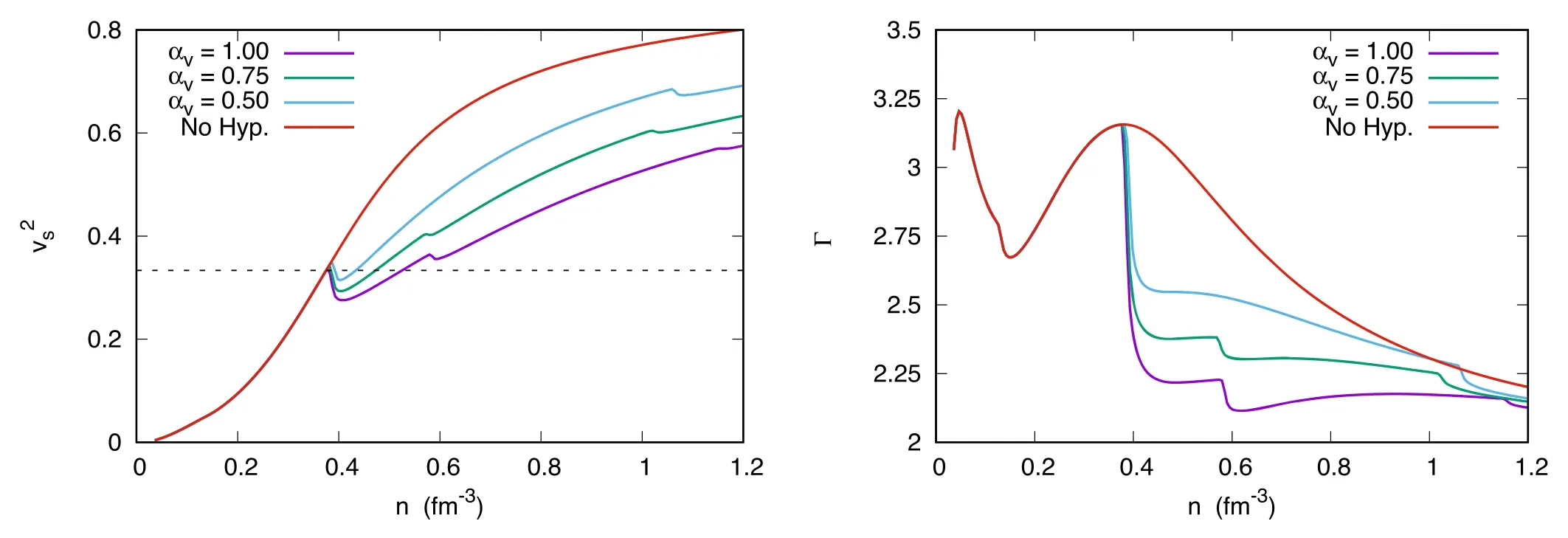
Figure 3.The speed of sound (left) and the adiabatic index Γ (right) for different values of αv.The horizontal dotted line is the conformal limit:

Another important physical quantity is the adiabatic index, Γ, a sensitive indicator of phase changes in stellar matter and the stability with respect to vibrations and pulsation of the star[44,45].For multicomponent matter,the exhibit jumps at densities coincident with density thresholds of individual components, signaling phase transitions and/or changes in the make-up of the matter [35].As shown in figure 3, the Λ0threshold is strongly evidenced, causing a huge drop in the value of Γ.A smaller but distinguishable peak around 0.6 fm−3points to the onset of the Σ−hyperon for αv= 1.00 and αv= 0.75.As pointed out earlier, for αv= 0.50, the Σ−is suppressed.

Concerning the neutron star properties and the astrophysical constraint, one of the most robust constraints is the minimum mass that an EoS must reproduce due to observational measures of massive stars via Shapiro delay.Not long ago,the neutron star king was the PSR J0348+0432,with a mass of 2.01 ± 0.04 M⊙[7].The old king was deposed, and now the PSR J0740+6620 with a mass of approximately 2.07±0.07 M⊙[46] rules over the sky.Notwithstanding,both pulsars send the same message: the EoS must be stiff enough to produce a two solar mass neutron star.On the other hand,one of the most controversial constraints is the radius of the canonical 1.4 M⊙.In the last couple of years, different studies point to different values for their maximum allowed value.For instance, maximum values of 13.8 km, 14.2 km,13.5 km, 12.6 km, 13.5 km, 12.8 km, 13.0 km, and 13.2 km were found,respectively,in[8,10,47–52].The average value of these studies is 13.32 km, and I use it as a constraint.

Also,as pointed out in[53],any acceptable EoS shall not allow the direct Urca process to occur in neutron stars with masses below 1.5 M⊙.The trigger to the nucleonic direct Urca channel is directly related to the leptonic fraction xDU.[22, 53].On the other hand, when hyperons are present the situation is more complex.Hyperons disfavor the direct urca(DU) process due to the deleptonization of the star, and the nucleonic DU process may be forbidden.However, channels for neutrino emission involving the hyperons are also possible, but with lower efficiency.As in this work, the Λ0is always the first and the most populous hyperon, and I only consider its process.The nucleonic,xDU=Yp,and hyperonic,=YΛ, fractions to enable the DU process are [54]:

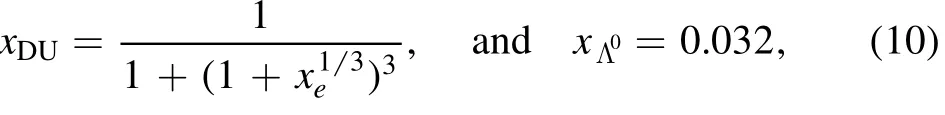
where xe= ne/(ne+nμ).Notwithstanding, the efficiency of the hyperonic DU process is only 4% of the nucleonic one [54].

Another important constraint comes from the GW170817 event, detected by the LIGO/VIRGO gravitational wave telescopes: the dimensionless tidal deformation parameter Λ.The tidal deformability of a compact object is a single parameter that quantifies how easily the object is deformed when subjected to an external tidal field.Larger tidal deformability indicates that the object is easily deformable.On the opposite side, a compact object with a smaller tidal deformability parameter is smaller,more compact,and it is more difficult to deform.Its value is defined as:Λ=2k2/3C5,where C=(GM/R) is the compactness.The parameter k2is called the Love number and is related to the metric perturbation.A complete discussion about the Love number and its calculation is both very extensive and well documented in the literature.Therefore, it is out of the scope of this work.I refer the interested reader to [29, 55–57] and the references therein.The authors in [29] constrain the dimensionless tidal parameter for the canonical mass Λ1.4in the range of 70-580.Here,I use 580 as a superior limit.

Finally, a very recent constraint comes from the measurement of the radius of the massive pulsar PSR J0740+6620 made by the NICER x-ray telescope.This is related to how squeezable the neutron stars are and allows us to put an inferior limit to the radius of a two solar mass object.Inferior bounds of 11.4 km, 12.2 km, 11.6 km and 12.2 km were found, respectively, in [28, 46, 58, 59].An average value of 11.85 km arises and I also use this value as a constraint to the EoS.

In figure 4, I display both the Tolman–Oppenheimer–Volkoff equation solution [60] and the calculated value for the dimensionless tidal parameter Λ.The Baym–Pethick–Sutherland EoS is used to model the neutron star crust [61].The hatched areas are the uncertainty about the mass value ofPSR J0740+6620 [46], as well as the uncertainty about the Λ1.4[29] value.The main neutron star properties and the astrophysical constraints are also displayed in table 3.

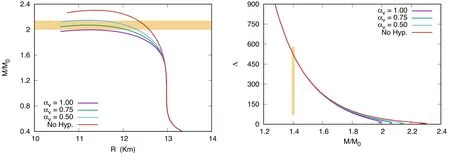
Figure 4.The mass radius relation(left)and the dimensionless tidal parameter Λ(right).The hatched area on the left(right)is related to the uncertainty about the mass of PSR J0740+6620 (uncertainty about the value of Λ1.4 in the GW170817 event [29]).

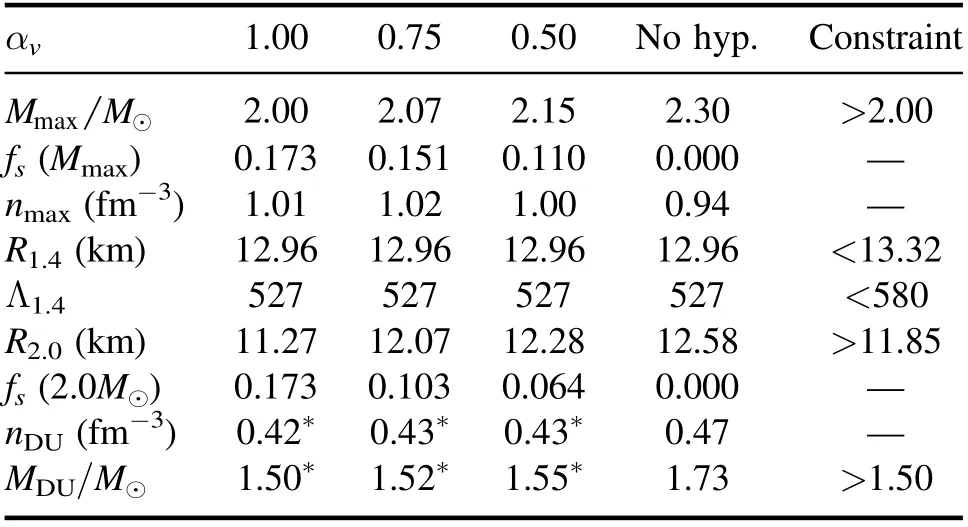
Table 3.Some neutron star properties and constraints for different values of αv.Results marked with ∗indicate a hyperonic DU process, with only 4% of the efficiency of the nucleonic DU.

As can be seen,even in the presence of hyperons,we are able to produce a two solar mass neutron star.Also, as hyperons are not present at masses around 1.4 M⊙, the R1.4and Λ1.4always give the values of 12.96 km and 527,respectively.This then means that besides correctly reproducing the six parameters of symmetric nuclear matter, this EoS also fulfills the main astrophysical constraints:Mmax>2.00M⊙, R1.4<13.32, MDU>1.50 M⊙, and Λ1.4<580.The only astrophysical constraint that is not satisfied for all models is the recent measure of the radius of the PSR J0740+6620,as αv=1.00 produces a too low radius for a 2.00 M⊙.Indeed, as can be seen in table 3, there is a relation between the maximum possible mass and the radius of the 2.00 M⊙.The higher the maximum mass,the higher the radius of 2.00 M⊙.This relation can be explained due to the different strangeness content in the core of the 2.00 M⊙star.The higher the value of fs, the softer the EoS, and the lower the radius of the 2.00 M⊙and the maximum mass.Also,when hyperons are present, the nucleonic DU process is always forbidden and only the hyperonic DU process is present.Without hyperons, nucleonic DU occurs for masses above 1.73 M⊙, which agrees with [53].

4.Final Remarks

In this work, I build a new EoS that can satisfy all six main constraints at the nuclear saturation point.This EoS is also able to fulfill the experimental constraint of the pressure at supra-nuclear densities for 85% of the interval presented in the combined [31, 32] and produces good values for S(2n0)and p(2n0), in agreement with [28, 29].

In the realm of astrophysical constraint, this EoS is able to reproduce masses above 2.00 M⊙,even when hyperons are present.It also produces R1.4< 13.32, km MDU>1.50 M⊙,Λ1.4<580 and R2.0>11.85, km; thus satisfying all the main astrophysical bounds.

The applications of this new parametrization can be extended in a large branch of areas.As I presented only infinite symmetric and beta-stable nuclear matter at zero temperature, results concerning finite temperature effects,finite nuclei,magnetic and electric fields,pasta phases,and so on are still open.

Before I finish, it is worth pointing out that PREX2 experiments have pointed toward much larger values for the slope L, as well as the tidal parameter Λ1.4and the radius of the canonical star [30].These results can be far beyond the most acceptable values coming from several different studies and still need confirmation.Nevertheless, if the PREX2 results turn out to be true, that does not imply a strong modification in the presented EoS.Only the gρ,Ncoupling constant and the Λωρparameter will need to be modified.The same is true if the slope needs to be lowered.

A similar case is a recent criticism in the results of [31]that I use as a constraint in figure 1.While[22,26,62]accept the results, using them as a constraint, others, as in [42],suggest that those results are flawed, as they do not take into account finite temperature effects,as well as the possibility of deconfinement.Nevertheless,the validity or not of the results from [31] will depend on additional HIC analyses.

Acknowledgments

The author is eternally grateful to Debora P.Menezes for her English corrections, and for almost seven years of tutelage.

ORCID iDs