基于轨道车辆轴箱加速度的动态轨道不平顺分析*

2022-02-18厉鑫波周劲松邓辰鑫

城市轨道交通研究 2022年1期

厉鑫波周劲松邓辰鑫孙煜

(1.绍兴市公路与运输管理中心，312099，绍兴；2.同济大学铁道与城市轨道交通研究院，201804，上海∥第一作者，工程师)

在无轮载作用下，测得的静态轨道不平顺仅能反映轨道表面几何不平顺以及部分道床与路基的不均匀残余变形导致的不平顺，而不能反映实际列车运行下的轨道附加变形和轮轨振动响应部分。真正对行车安全、轮轨作用力及车辆振动产生影响的是动态轨道不平顺。随着我国轨道交通的快速发展，运行速度、载重和发车频次大幅度提升，在高密度线路上实现动态轨道不平顺的实时在线监测，为线路维护工作提供科学依据[1]，提高旅客乘坐舒适性，具有重要的现实意义。位移、速度和加速度等振动参数常常用于故障诊断和运行状态监控[2]。加速度信号采集的使用则更为普遍，因为其设备体积小、易安装、可靠性高并且测试准确。但是对振动系统进行分析时，速度和位移信号也是很重要的[3-4]。轨道车辆上的轴箱振动加速度信号，经过二次积分后可用来计算轨道不平顺[5]。因此，对振动信号积分的计算涉及很多工程实例，具有研究价值。

目前对加速度进行积分的算法主要有频域积分法和时域积分法[6]。频域积分法是利用傅里叶变换及其逆变换，把积分过程用分量系数来表示，并且在频域内进行幅值控制。该方法能避开时域微小误差的累积效应，但幅值控制函数是频域积分算法的难点。时域积分主要采用数值积分公式，但受信号基线的影响，往往需要添加滤波和进行去除趋势项处理。尽管如此，误差累积效应难以根除。微小误差在两次积分过程中会使信号波形产生畸变[7]。文献[8]基于误差理论，针对加速度积分过程中的误差信号提出误差公式，认为误差来源主要是加速度传感器的测量误差，且信号的低频峰值对误差的影响尤为巨大。尽管如此，由于时域积分的简洁和快速，在轨道检测系统[5]中使用最多的仍然是时域积分算法。

本文研究了加速度信号处理技术，旨在通过时域积分方法获得位移，实现实测数据和标准中的数据的对比。采用均差牛顿插值法[9]对信号插值进行处理，再使用辛普森公式对时域数据进行积分，过程中通过最小二乘法拟合剔除趋势项[6]，并利用简谐叠加信号进行检验和误差计算。同时，建立引入轨道不平顺的单轮轨模型，说明一系簧下质量的加速度响应能够反映动态轨道不平顺。随后，以上海轨道交通某线的地铁车辆为研究对象，排查车轮踏面情况对于轴箱振动的影响，实测其运行于不同线路上的轴箱振动数据，再通过积分运算获得位移信号，绘制不平顺预测谱，并与美国五级谱进行对比。最后，通过比较不同线路的车辆运行平稳性指标，验证动态轨道不平顺计算方法的有效性。

1 加速度积分原理

1.1 时域积分

记加速度信号序列(tn,an)，n=0, 1,…,Na-1，采用辛普森法数值积分公式[10]进行积分。为了不降低积分后的数据频率，利用均差的牛顿插值法[9]对中间项进行估计。整理后，加速度信号Ik可表示为：

(1)

式中：

Δt——时间增量；

ak——当n=k时的加速度幅。

记速度信号序列(tn,vn)，所以：

(2)

式中：

v0——初始速度。

其中，n=0, 1,…,Nv-1。同理可得位移信号。

1.2 剔除趋势项

以积分后的速度信号为例，用最小二乘法[10]拟合出趋势项，假设存在最高处为m次的多项式fm(t)：

(3)

存在一组系数pk，使得式(4)取得最小值。

(4)

故：

(5)

其中，j=0, 1,…,m。对上式变形，并用矩阵表达可得：

(6)

式(6)存在唯一解，即拟合系数pk。处理后的速度信号v′k可表示为，

v′k=vk-fm(tk)

(7)

1.3 误差计算

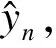
(8)

绝对误差越小，就意味预测结果更准确。

决定系数R2反应了预测数据和原始数据的吻合程度，常用于回归分析。

(9)

式中：

决定系数R2可以用来量化预测模型的表现，被当作衡量预测模型能力好坏的标准。R2的数值范围从0至1，表示目标变量的预测值和实际值之间的相关程度。R2值越接近1，表示预测值对原始变量的预测越准确。

1.4 算法验证

假设输入的加速度信号为简谐振动叠加的信号a(t)，其表达式为：

(10)

同理可得位移信号。图1所示为该算例的流程图。在第一次积分后，选择去除线性趋势项。在第二次积分后，选择去除二次趋势项，这是由于趋势项往往会有残留，在积分后误差会被放大。

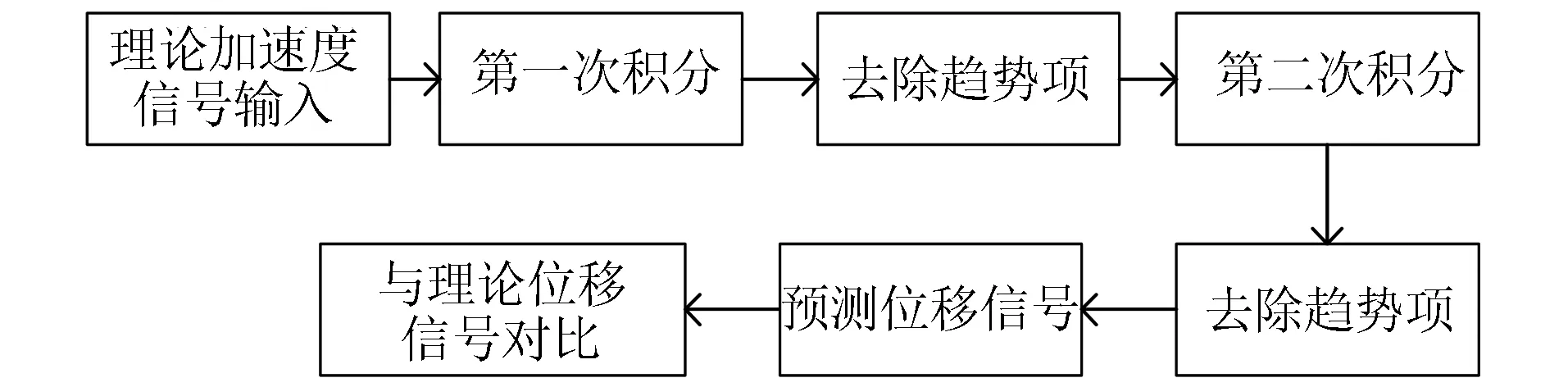
图1 信号处理流程图

图2 a)为原始加速度信号，图2 b)为理论位移信号和预测位移信号。由图2易知，预测值曲线和理论值曲线基本重合，说明了所用方法在一定数量简谐振动叠加的信号情况下有很高的精度。

图2 加速度信号和位移信号对比图

选取不同的采样比，分析采样比对误差的影响。图3为绝对误差和决定系数随采样比变化的关系图。由图3可知，当采样比大于2时，绝对误差随采样比的增大而减小，决定系数随采样比的增大而增大，且变化趋势随之缓慢。当采样比为3时，绝对误差为6.28%，决定系数为0.985，说明当前预测模型达到了很高的拟合度，预测位移信号是可信的。当采样频率大于5时，计算结果趋于稳定。

图3 绝对误差和决定系数随采样比变化的关系图

2 基于实测数据的动态轨道不平顺分析

2.1 引入轨道不平顺的单轮轨模型

在建立单轮轨模型时，可将包含轴箱、轮对的一系簧下质量和轨道分别简化为单自由度的当量系统，且不考虑一系悬架以上部分的影响。这是因为在实际运行工况中，轮轨间高频响应的频带远大于构架及车体的自振频率。模型中假设车体、构架不随轴箱上下运动而静止，轮轨始终保持接触，且具有一定的接触刚度。轨道垂向不平顺以位移的形式作为系统的输入。引入轨道不平顺的单轮轨模型如图4所示。

基于图4模型的垂向动力学方程为：

图4 引入轨道不平顺的单轮轨模型

(11)

式中：

钢轨波浪形磨耗作为最普遍的不平顺表现，具有谐波特征，可用式(12)表示：

(12)

式中：

b——常量；

ω——角频率。

在假设的零初始条件下，对式(11)进行拉普拉斯变换并化简，可得：

(13)

式中：

s——拉普拉斯变换复变量。

由此可得一系簧下质量的位移传递函数HZ1为：

(14)

故一系簧下质量的加速度响应为:

(15)

轮轨接触刚度、钢轨支承刚度和阻尼都相对一系悬架的刚度和阻尼大的多，所以传递函数HZ1的特征方程的所有系数都为正，根据劳斯判据，所有根的实部为负。假设传递函数HZ1有各不相同的实数极点，记pi(i=1,2，…，n)，则式(15)可写成：

(16)

式中：

Ai，pi，B，C——由系统参数和输入参数决定的常数。

对式(16)进行拉普拉斯逆变换，得到：

(17)

式中，

(18)

(19)

式中：

φ——初相位。

式(17)中，第一项为衰减项，随着时间的增加而衰减为零，第二项为稳态项。可见，在谐波型轨道垂向不平顺输入下，一系簧下质量的加速度响应的频率不失真；而加速度响应的幅值是输入信号的幅值与频率特性的幅值的乘积，包含了轮轨作用力和轨道附加变形的动态轨道不平顺。因此，一系簧下质量的加速度响应能够较准确地反映出动态轨道不平顺状况。

2.2 测试方案

为了探究实际路线上轴箱的振动情况和轨道不平顺，对某运营线的地铁车辆进行轴箱振动测试和分析。测试线路包含旧线和试运营的新线，两条线路开通时间相差近15年，由于使用和日常维护情况不同，线路状况相差甚远。测试车辆为新车，车辆各方面状态最佳。为了排查车轮偏磨、多边形磨损等对轴箱振动情况的影响，对车轮踏面进行检测。测试时，在TC车的一、二位侧的对等轴箱上布置加速度传感器，并在该车车体一、二位端地板的平稳性测点上布置加速度传感器。测试工况为同一车辆以80 km/h在旧线和新线的平直区段内分别运行。测试仪器如表1所示，轴箱及车体地板测点如图5所示，车轮踏面测试如图6所示。

表1 测试仪器

图5 轴箱及车体地板测点图

图6 车轮踏面测试图

2.3 数据处理与结果分析

2.3.1 车轮踏面计算

车轮旋转一周，车轮粗糙度测试仪探针记录车轮踏面径向波动量。以车轮踏面平均径跳量为基准，绘制车轮踏面圆周粗糙度。一般径跳量在100 μm以内的车轮为新轮或新镟修车轮。如图7所示，一位侧轮的最大径跳量为23.2 μm，最小径跳量为-6.2 μm；二位侧轮的最大径跳量为8.7 μm，最小径跳量为-11.9 μm。两侧车轮没有明显的偏磨。

图7 车轮踏面粗糙度极坐标图

为了研究车轮多边形磨损，通常对车轮踏面圆周粗糙度进行阶次分析，粗糙度水平用dB表示，其表达式为：

(20)

式中：

Lk——k阶踏面粗糙度；

rk——k阶踏面粗糙度均值；

rref——参考值，取值为1 μm。

图8为车轮踏面粗糙度阶次图。如图8所示，一、二位侧车轮踏面粗糙度水平在所示阶次域中均处于较低水平，且没有显著的单峰值，说明两侧车轮没表现出多边形磨损特征，服役状态良好。

图8 车轮踏面粗糙度阶次图

2.3.2 轨道预测谱计算

利用加速度积分原理，对两侧轴箱加速度信号积分后取平均值，则可得到轨道垂向不平顺[4]，其表达式为：

zv=(zl+zr)/2

(21)

式中：

zv——轨道垂向不平顺；

zl——左轨垂向不平顺；

zr——右轨垂向不平顺。

图9为车辆在旧线和新线上运行时，两侧轴箱加速度信号和积分后的预测位移信号。由图9可见，在所截取的里程内，预测位移信号在旧线上的幅值显著大于新线。

图9 轴箱加速度信号和预测位移信号图

美国轨道谱的解析式[4]为：

(22)

式中：

Sv——功率谱值；

Av——粗糙度系数；

K——比例系数；

Ωc——截断频率；

Ω——空间频率。

将预测位移信号功率谱与美国五级谱进行对比，结果如图10所示。旧线和新线的预测谱与美国五级谱具有类似的趋势。旧线的预测谱幅值在所示空间频率范围内明显大于新线的预测谱，说明旧线轨道不平顺状态劣于新线。新线的预测谱在空间频率为2.4 rad/m处出现显著的波峰。而通常波长在1.0～3.5 m范围内，波幅在0.1～1.0 mm范围内的波长成分，主要是钢轨在轧制过程中形成的周期性成分，属于新轨轨身不平顺。旧线的预测谱在空间频率为16～28 rad/m波段出现显著的波峰。而通常波长在几百毫米内、波幅在2 mm以内的波长成分，主要由钢轨波浪形磨耗和轨枕间距不平顺引起[13]。

图10 预测位移信号功率谱与美国五级谱对比图

由于加速度传感器的低频非线性，轨道预测谱在低于0.5 Hz的低频长波部分会产生失真。受轮轨接触斑沿钢轨纵向长度限制，无法识别出半波长小于该长度的轨道不平顺。预测谱在高频短波部分也会产生失真。而在中高频段的预测谱具有较高的识别可靠性。

2.3.3 车辆平稳性计算

根据GB 5599—1985，运行平稳性指标计算公式：

(23)

式中：

W——平稳性指标；

A——振动加速度；

f——振动频率；

F(f)——频率修正系数，频率修正系数表详见标准。

任意截取不同线路上车体一、二位端处的20 s垂向加速度数据进行计算，平稳性指标计算结果如表2所示。由表2可知，在旧线上，车体一、二位端的平稳性指标在2.50至2.75之间，平稳性等级为2级，评定为良好。在新线上，车体一、二位端的平稳性指标小于2.50，平稳性等级为1级，评定为优。在车辆运行工况一致的前提下，运行于旧线的平稳性明显劣于新线，说明旧线的动态轨道不平顺水平显著高于新线。