基于混洗差分的Web查询大数据隐私保护方法

虞 娟

(马鞍山师范高等专科学校 软件工程系，安徽 马鞍山 243000)

随着科技和互联网的不断发展，Web网络中的海量数据成为一笔巨大的财富。信息化时代的发展潮流是利用这些数据对各行各业的状态进行分析实现数据共享[1-2]。然而数据共享时对Web大数据进行查询过程中，会导致个人隐私泄露的概率加大。因此，Web查询大数据的隐私保护受到普遍重视[3-4]。

大数据的隐私保护成为研究人员的研究主题。例如周艺华等人提出通过GeoHash算法用字符串代替查询用户的位置，并构建Trie前缀树，LBS服务器在前缀树的基础上匹配字符串，然后发送给用户，通过此过程保护用户信息，但是该方法只保护查询用户的位置信息，并未对查询的数据进行隐私保护[5]。顾一鸣等人通过预先缓存机制实现连续查询数据的隐私保护，其可有效处理连续查询过程中出现的最大移动边界攻击问题，通过预先缓存的方法使得连续查询数据的时间关联度降低，增强数据隐私保护水平，但是该种方法隐私保护过程中未进行数据冗余的过滤处理，导致数据隐私保护效果大大降低[6]。

混洗差分隐私模型将洗牌者插入大数据和数据收集者之中，洗牌者接收混入噪声的数据，并将其混洗，然后输送给收集者分析，用户和大数据之间关联性通过洗牌操作切断，有效地实现大数据的隐私保护[7]。

因此，本文提出一种基于混洗差分的Web查询大数据隐私保护方法，保护查询大数据隐私不被泄露。

1 Web查询大数据隐私保护

在大数据环境的Web查询系统中，由于一些查询的数据具有关联性，数据存在冗余现象。为了减少冗余数据量，通过关联性分析删去关联数据[8-9]，减少大规模数据的数据量。此外在查询数据时，不仅需要提高查询系统的数据处理速度[10]，而且需要对查询数据进行隐私保护，综合以上问题，本文提出基于混洗差分的Web查询大数据隐私保护方法。

基于混洗差分的Web查询大数据隐私保护方法包括3个子模型：基于最大信息系数的特征选择模型(MICFS)、并行梯度下降矩阵分解模型(PGMDM)和基于混洗差分的洗牌者多维扰动发布模型。

Web查询大数据隐私保护过程如下：

(1)查询数据集；

(2)通过MICFS求解数据间的相关性并设定阈值，将无关性数据构建成特征数据集；

(3)根据特征数据集构建相关性低的无关负载矩阵，通过并行梯度下降矩阵分解模型分解该无关负载矩阵；

(4)通过基于混洗差分的洗牌者多维扰动发布模型实现无关负载矩阵的隐私保护；

(5)发送添加扰动后的结果给查询者。

1.1 基于最大信息系数的特征选择模型的冗余数据处理

Web查询系统具有数据量大、查询次数多的特点，为了提高Web查询大数据查询的提取速度，依据用户的查询信息构建一个查询数据集。根据最大信息系数和启发式搜索算法，在该查询数据集里，设定特征和类别、特征和特征的关联性，将无关性数据构建成特征集。利用基于最大信息系数的特征选择模型，去掉冗余数据。

设定存在一个n条样本的Web查询大数据特征集，用m表示特征数，用c表示类别。特征集表示为：F={f1,f2,…,fm,c}。用MIC(fi,c)表示任意特征fi和类别c的相关性，且MIC(fi,c)∈[0,1]。MIC(fi,c)值的大小，决定fi和c的相关性的强弱，其值越大，相关性越强，此时的fi是强相关特征；其值越小，相关性越弱，此时的fi是弱相关特征。用MIC(fi,fj)描述fi与fj的相关性，fi和fj的可替代性随着MIC(fi,fj)值的增大而增强，若MIC(fi,fj)=0，则fi和fj没有可替代性，二者之间相互独立。

利用MICFS对数据集的无关性处理。该过程通过以下5步实现，流程图如图1所示。

(1)在n条样本的特征F={f1,f2,…,fm,c}中，确定其原始数据集D和空集B。

(2)求解该特征集中特征fi和类别c的最大值MIC(fi,c)。

(3)将第(2)步中的最大值当作初始变量，D=D-(fi)，B=B+(fi)。

(4)通过贪心算法求解出fi和fj中的最大值MIC(fB,fi)，将其当成下个候选变量，求解出新候选变量的最大值如式(1)所示。

(1)

(5)重复操作第(4)步，选定特征的个数等于设定值时结束操作，并用选定的特征构建数据集B。

1.2 基于并行梯度下降矩阵分解模型的Web查询大数据的快速提取

用户通过Web查询系统查询数据时，存在数据量多以及查询回合多的问题，是一种批量线性查询过程。为了进一步提高用户对Web查询大数据的提取速度，通过融合交替方向乘子法和低秩机制形成的并行梯度下降矩阵分解模型，将分解后的查询数据无关负载矩阵并行处理，减少Web查询大数据的查询时间[11-12]。

(2)

(3)

其中，W表示根据特征数据集B构建无关负载矩阵；将W分解成A和L两个矩阵；β表示分解系数。A是随着L的更新而更新，式(2)用来计算A。

并行梯度下降矩阵分解模型以矩阵的特性为基础，将W分解成多个矩阵，并将这些矩阵分别发放到各个节点上，并完成计算。矩阵分解过程如图2所示。

PGMDM主要通过以下几步完成。

(1)以用户查询要求为基础，构建初始结果负载矩阵。

(2)以通过基于最大信息系数的特征选择模型得出关联属性为依据，初始化查询数据的负载矩阵，删去负载矩阵中有关联的数据，形成无关负载矩阵。

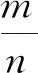
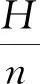
1.3 基于混洗差分的查询数据隐私保护模型

1.3.1 混洗差分隐私

通过Randomized Response(RR)机制扰动真实数据。本地化差分隐私模型(LDP)利用RR机制完成自身数据扰动，进而实现Web查询大数据的隐私保护。RR机制定义为：已知值域D={1,2,…,d}，用户发送真实值概率为p，任意选取值域内一个数值的概率为q。RR机制符合如式(4)所示。

(4)

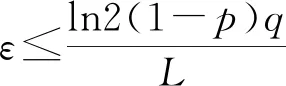
混洗差分隐私将并行梯度下降矩阵分解模型后的无关负载矩阵L中的数据，作为用户ui的Web查询数据，将这些查询数据作为数据集[14]，ti为ui中的数据且ti∈V。所有用户ui符合εl的本地化差分隐私算法R:V→Y扰动vi:yi=R(vi)。受扰动后，n个用户的扰动结果用O={y1,y2,…,yn}描述，第i个用户的扰动结果用yi描述[15]，洗牌者对yi随机洗牌操作用S:Yi→Yn描述。以上两步的结合用机制M=R○S描述，M符合(εc,δ)混洗差分隐私。当且仅当针对任意数据集D和D′(二者之间仅相差一个用户数据)，任意输出集合Y′⊂Yn，存在式(5)。

Pr[M(D)∈y′]≤δ+eεc×Pr[M(D′)∈y′]

(5)

在混洗差分隐私模型中，隐私毯子为用户根据查询得到的随机答复。本地化差分隐私模型形成的分布可分解为真实值分布和随机独立分布(隐私毯子)，此过程叫做隐私毯子分解。式(5)可分解为如式(6)所示。

[RR(v)=y]=γPr[Uni(D)=y]+

(1-γ)PrV(y)

(6)

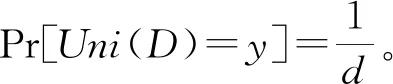
由于大数据中具有多维数据，维度高与取值域异构的多维数据导致发布过程困难，因此本文提出基于混洗差分的洗牌者多维扰动发布模型解决此问题，实现大数据的隐私保护。

1.3.2 基于混洗差分的洗牌者多维扰动发布模型

混洗差分通过洗牌操作可对用户同带噪数据间的关联性进行打乱操作，增强数据隐私保护性。因此，通过基于混洗差分的洗牌者多维扰动发布模型，实现Web查询大数据的隐私保护。

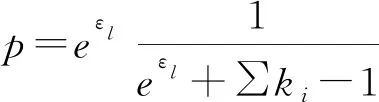
通过统计数据的频率分布，收集者以带噪数据维度为基础，并对其编号，再根据编号分组，得出第i个属性取值是v的频率信息如式(7)所示。

(7)

收集者依据洗牌后的数据完成频率估计，依据该估计结果获取误差平方和SSE(sum square error)，通过SSE分析扰动的web大数据发布结果。本文提出满足混洗差分隐私的多维类型数据频率估计方法，可最大程度降低web大数据隐私保护的消耗，最大程度的确保大数据隐私保护时，发布的扰动数据误差最小，且存在式(8)。

(8)

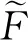
2 实验分析

实验以某Web网络中的查询数据集：Kosarak数据集(二进制)和Mexico数据集(非二进制)为实验对象，描述数据的具体信息如表1所示。

表1 数据集

采用本文方法在不同的无关性系数情况下，分析Mexico数据集和Kosarak数据集的无关性，结果分别如表2所示。

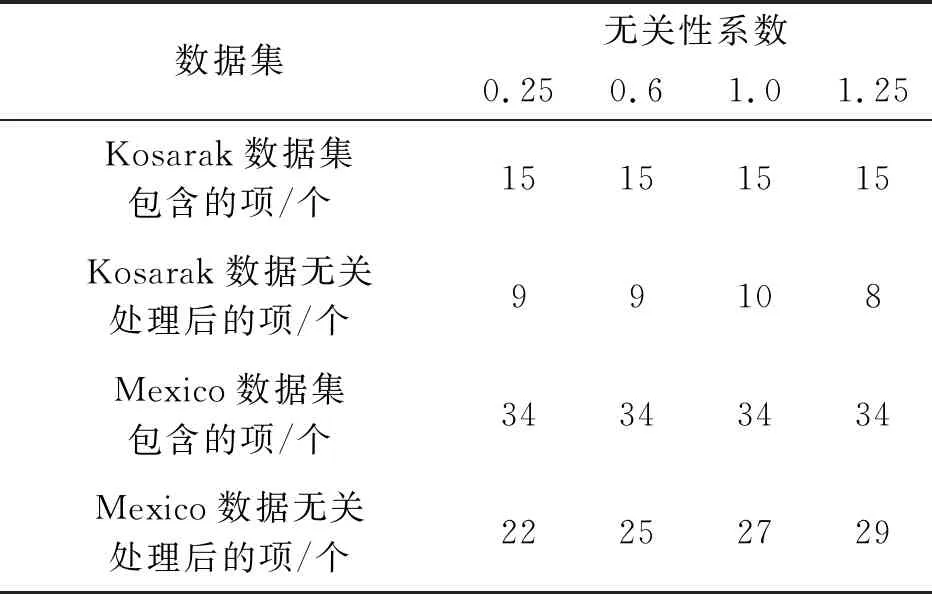
表2 数据集数据无关性分析

通过表1、表2可以看出，经过本文方法对Kosarak和Mexico数据集进行数据无关处理后，在不同取值的无关性系数下，Kosarak和Mexico数据集包含的项均显著减少，说明本文方法有效降低了实验Web大数据集中的冗余数据，为后续数据隐私保护提供可靠的基础。

本次实验验证本文方法对Kosarak数据集和Mexico数据集的隐私保护能力，实验改变隐私预算εc的值，通过误差平方和(SSE)分析本文方法对两种实验数据集中数据的混洗扰动发布结果，结果如图3所示。

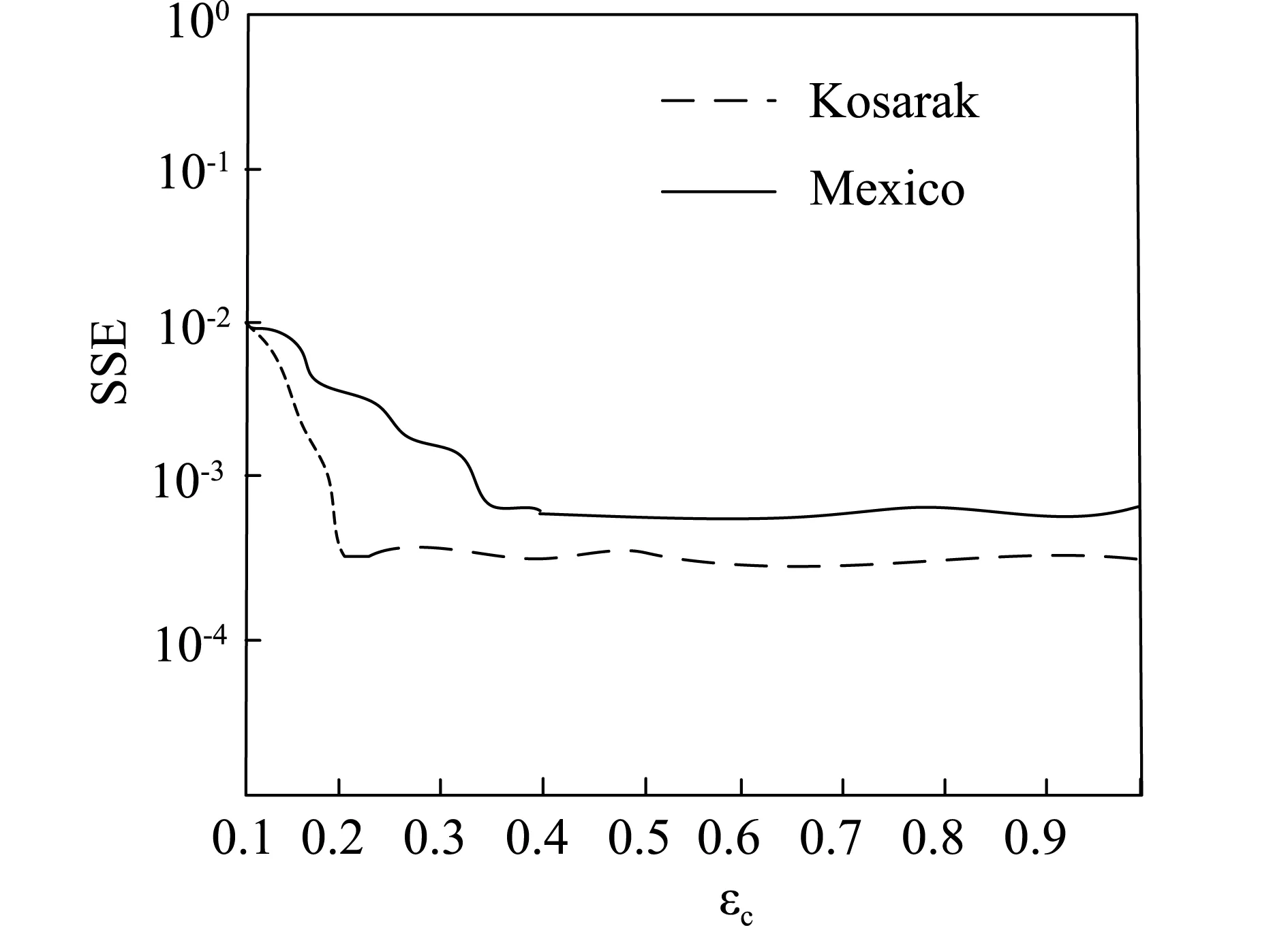
图3 隐私保护结果

由图3可以看出，采用本文方法对Kosarak数据集隐私保护时，在εc<0.2时，隐私数据扰动发布的SSE逐渐减小，εc≥0.2时SSE趋于稳定，数据扰动发布保护效果越好。采用本文方法对Mexico数据集进行隐私保护时，在εc<0.4时，隐私数据扰动发布的SSE逐渐减小，εc≥0.4时SSE趋于稳定，数据扰动发布保护效果越好。

本文方法对Mexico数据集中包含网络数据进行隐私保护，保护前后的对比结果见图4。

(a)保护前

通过图4实验结果可以看出，本文方法可以实现Web网络查询信息的保护处理，保护后的网络信息安全性高，不易被非法者窥探。

以保护后的Web查询大数据隐私被攻击捕获概率作为衡量指标，随机选取Mexico数据集，测试该数据集在不同查询数据规模时，Web查询数据在被本文方法保护前后的被捕获概率，结果用图5描述。

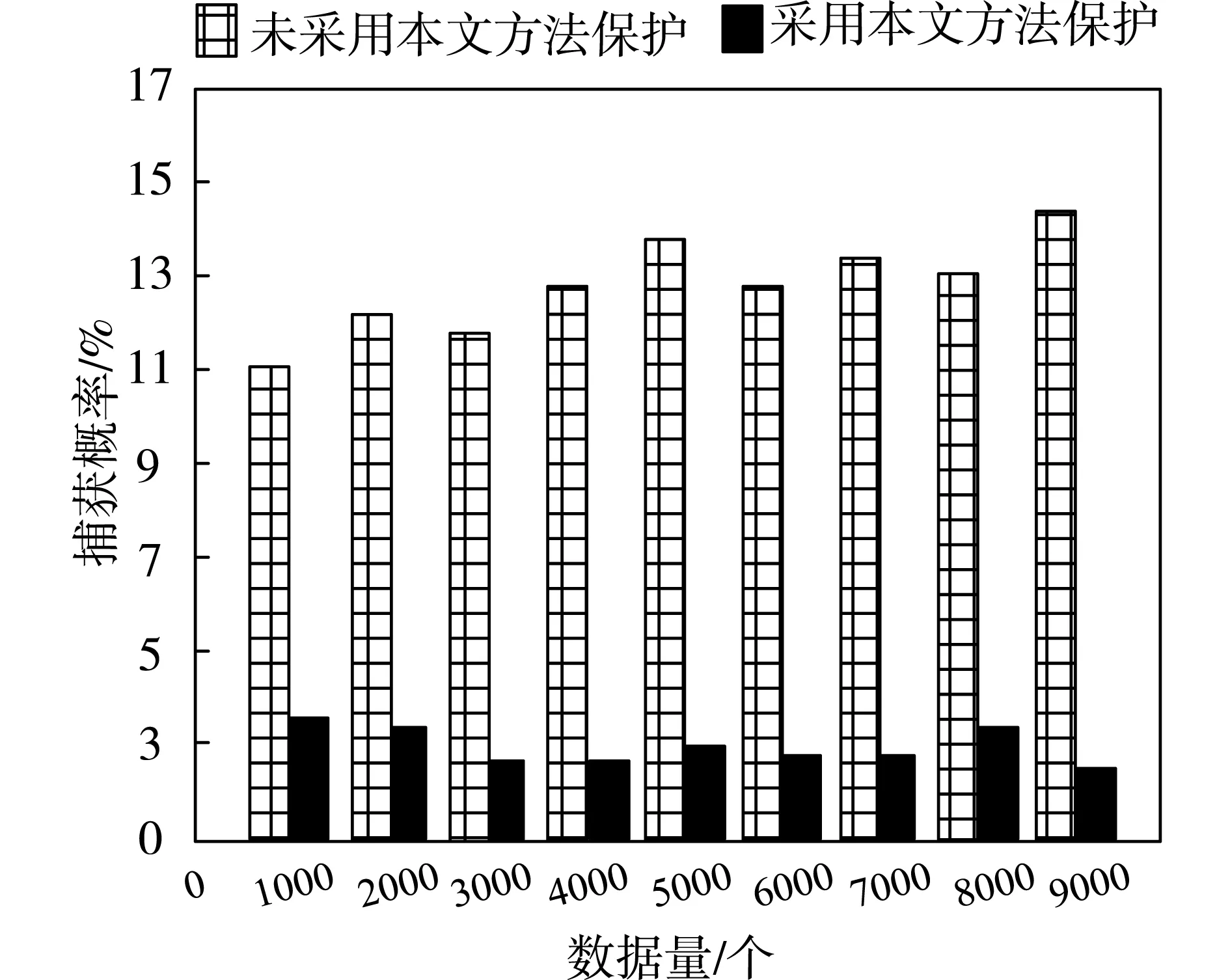
图5 捕获概率统计

分析图5可以看出，当Web查询数据规模不同时，数据隐私被捕获的概率出现无规律分布状态，主要是因为Web网络的攻击类型具有多样性，导致攻击捕获数据隐私的概率也呈现出无规则状态。当数据量相同时，采用本文方法进行隐私保护后数据隐私被攻击捕获的概率，远远低于未采用本文方法进行隐私保护的数据隐私被捕获的概率。该结果说明：本文方法可有效降低Web查询大数据隐私被捕获的概率。

3 结论

在Web查询大数据隐私保护中引入混洗差分的方法，提出基于混洗差分的Web查询大数据隐私保护方法。该方法通过基于最大信息系数的特征选择模型、并行梯度下降矩阵分解模型和基于混洗差分的洗牌者多维扰动发布模型实现Web查询大数据隐私保护，为Web查询大数据隐私保护提供一种新方法，未来在查询大数据隐私保护问题上可大量应用本文方法。