有限FI代数的矩阵表示

韦安丽, 李 莹, 赵建立, 丁文旭

(聊城大学数学科学学院/矩阵半张量积理论与应用研究中心, 聊城 252000)

模糊蕴涵代数[1],简称FI代数,揭示了蕴涵算子的本质。众多著名的模糊逻辑代数系统,如MV代数[2]、BL代数[3]、R0代数[4]、剩余格[5]和格蕴涵代数[6]等，都是FI代数的特殊子类代数。

迄今为止,许多科学工作者从事这方面的研究并取得了丰硕成果[7-14]。例如，王国俊[7]证明了3种不同形式的 MV-代数刻画的等价性,同时分析了 MV-代数、BL-代数和R0代数的逻辑背景；ZHU和XU[9]发展了一般剩余格的滤波理论；裴道武等[10]揭示了FI格与模糊逻辑中几个重要代数系统之间的紧密联系,且一些重要的模糊逻辑代数系统都是FI格类的子类；吴达[13]在FI代数中引进“交换”运算，从而得到了进一步刻画FI代数及HFI代数的若干结果。

矩阵半张量积是一种新的矩阵乘积,是描述有限集上映射的强大工具,已成功应用于布尔网络[15]、密码学[16]、图着色[17]、信息安全[18]和车辆控制[19]等领域。基于此,本文将矩阵半张量积应用于逻辑代数研究领域,给出了FI代数的若干等价刻画：通过矩阵半张量积方法在统一的理论框架内刻画了有限FI代数;利用矩阵表达式,将有限FI代数上抽象的逻辑运算规律转化为具体逻辑矩阵的简单运算;彻底解决了有限FI代数同构的分类问题。

1 预备知识

定义1[20]对于矩阵A=(aij)m×n,B=(bij)p×q,定义A和B的Kronecker积为：

定义2[20]设矩阵Am×n,Bp×q,定义A与B的半张量积为

矩阵半张量积具有下列性质：

引理1[20]设A,B,C是实矩阵,a,b,则

(3)设xm,yn,则xy=x⊗y。

引理 2[20]设xt,Am×n,则xA=(It⊗Ax。

定义3[21]换位矩阵W[m,n]mn×mn定义为

换位矩阵的作用是交换2个不同维的列向量因子在矩阵半张量积运算下的顺序。

引理3[21]设xm,yn,则W[m,n]xy=yx。

则称这种表达为有限集的向量表达式,其对应顺序可以任意指定。

例如，在经典逻辑中,D={0,1},一个逻辑变量xD可以用向量形式表示:

类似地,经典逻辑变量的向量表达式也可以用于多值逻辑。

例1考虑k值逻辑,定义

基于此,有

利用向量表达式,一个n维变量逻辑函数f:Dn→D可以表示为从Δn到Δ的一个映射。

引理4[22]设映射f:Dn→D,利用向量表达式,有

其中Mf2×2n是唯一的,叫做f的结构矩阵。

计算显示Mc=δ2[1222]。类似地,可以得到Md=δ2[1112]和Mn=δ2[21]。

2 有限FI代数的矩阵表示

定义4[1]一个(2,0)型代数(X,→,0)称为模糊蕴涵代数,简称为FI代数,如果对任意x,y,zX,有

其中1=0→0。

(I1)′M→(t)(It⊗M→(t))=M→(t)(It⊗M→(t))W[t,t];

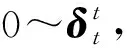
M→(t)(M→(t)xy)(M→(t)(M→(t)yz)(M→(t)xz))=

即

(M→(t))2(It2⊗(M→(t))2)xy2z(M→(t)xz)=

进一步可得

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))xy2zxz=

则有

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))x×

从而

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))×

故

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))×

(It⊗W[t,t3])PRt(It⊗PRt)(It2⊗PRt)xyz=

由x、y、z的任意性，可得

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))×

(It⊗W[t,t3])PRt(It⊗PRt)(It2⊗PRt)=

由此可知条件(I2)′等价于条件(I2)。证毕。

例3设t=2,由于→为一个二元算子,故可设M→(2)=[m1,m2,m3,m4](miΔ,i=1,2,3,4),只有唯一的一组M→(2)满足定理1的条件(I1)′～(I5)′,即

例4设t=3,类比上述步骤,运用穷举法只得到4组满足FI代数的定义的M→(3)：

可以在FI代数(X,→,0)上定义一个二元关系≤：

x≤y⟺x→y=1 (x,yX)。

显然,由→诱导的关系≤是一个偏序。

引理5[10]设(X,→,0)是一个FI代数,对于任意x,y,zX,下列性质成立：

对于有限FI代数,利用结构矩阵M→(t)与矩阵半张量积,可以将引理5的(i)～(vi)由定性运算转化为定量运算,给出它们的代数表达式。

定理2设(X,→,0)是一个有限FI代数,且|X|=t<∞。对于FI代数上的偏序关系进行矩阵表示，得到

由此二元关系可得到与引理5的(i)～(vi)等价的代数表达形式：

证明(i)′～(vi)′的证明方法类似,这里只给出(vi)′的详细证明。首先,可将(vi)等价表达成(y→z)→((x→y)→(x→z))=1,其矩阵表示如下：

M→(t)(M→(t)yz)[M→(t)(M→(t)xy)(M→(t)xz)]=

即

从而

(M→(t))2(It2⊗(M→(t))2)yzxyM→(t)xz=

进一步可得

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))yzxyxz=

则有

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))W[t3,t2]xyxyz2=

即

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))W[t3,t2]×

从而

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))W[t3,t2]×

则

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))W[t3,t2]×

(It⊗W[t,t])PRt(It⊗PRt)(It2⊗PRt)xyz=

由x,y,z的任意性,则有

(M→(t))2(It2⊗(M→(t))2)(It4⊗M→(t))W[t3,t2]×

(It⊗W[t,t])PRt(It⊗PRt)(It2⊗PRt)=

从而,(vi)′得证。证毕。

3 FI代数的同态与同构

定义5[1]设Fi=(Xi,→i,0i)(i=1,2)是2个FI代数,若存在映射f:X1→X2,使得

(i)f(x→1y)=f(x)→2f(y)(x,yX1);

(ii)f(01)=02,

则称f为FI代数同态。

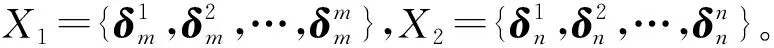
f(x)=Mfx,

其中Mfn×m是f的结构矩阵。

定理3设Fi=(Xi,→i,0i)(i=1,2)是2个有限FI代数,且|X1|=m<∞,|X2|=n<∞,存在映射f:X1→X2,f为FI代数同态当且仅当

(i)′MfM→(m)=M→(n)Mf(Im⊗Mf);

证明利用矩阵表示易得定理3的条件(i)′、(ii)′分别等价于定义5的条件(i)、(ii)。 证明过程如下：∀x,yX1,条件(i)的矩阵表示如下：

Mf(M→(m)xy)=M→(n)(Mfx)(Mfy),

MfM→(m)=M→(n)Mf(Im⊗Mf)。

从而证得条件(ii)′与条件(ii)等价。证毕。

定义6[1]设Fi=(Xi,→i,0i)(i=1,2)是2个FI代数,且映射f:X1→X2为FI代数同态,如果f是一对一且映上的,那么f称为FI代数同构。

定义7[20]给定一个置换τSn,定义它的结构矩阵Mτ如下：

称Mτ为置换矩阵。

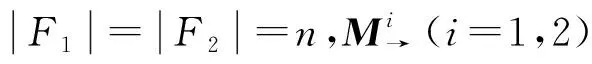
(i)T是一个置换矩阵,即存在一个置换τSn,使得T=Mτ,因此TT=T-1;

证明由定义6知,映射f:X1→X2是一对一且映上的,则存在一个τSn,使得f(i)=τ(i)(i=1,2,…,n)。 当x=iDn表示为向量形式时,有f(i)=(〗τ(i)=)〗Mτ(x)。于是

从而可得

证毕。

例5在例3中,当n=2时,没有非平凡同构。

4 FI代数的导子

本节利用矩阵半张量积与逻辑矩阵运算来考虑有限FI代数上的导子：首先，引入(l,r)-导子、(r,l)-导子和导子的概念,并给出它们的一些性质；然后，利用矩阵表达式,将d、⊕、→所满足的运算规律转化为具体逻辑矩阵的简单运算；最后，通过逻辑矩阵运算给出FI代数关于导子的新性质。

定义8[23]设(X,→,0)是FI代数,对于映射d:X→X：

(i)若d满足:∀x,yX,有

d(x→y)=(d(x)→y)⊕(x→d(y)),

则称d是X上的(l,r)-导子;

(ii)若d满足:∀x,yX,有

d(x→y)=(x→d(y))⊕(d(x)→y),

则称d是X上的(r,l)-导子;

(iii)若d既是X上的(l,r)-导子,又是X上的(r,l)-导子,则称d是X上的导子,并称(X,d)是导子FI代数;

(iv)若d满足∀xX,有d(x)=1,则称d是X上的平凡导子。

利用矩阵半张量积以及矩阵表达式研究有限FI代数上的导子时,定义一种新的二元运算⊕：∀x,yX,x⊕y=x′→y,其中x′是x的伪补,满足∀xX,x′=x→0。Md、M⊕(t)分别是d、⊕的结构矩阵,且由⊕所满足的运算规律,可以得到

定理5设(X,→,0)是有限FI代数,且|X|=t<∞,对于映射d:X→X：

(i)′d是X上的(l,r)-导子当且仅当

MdM→(t)=M⊕(t)M→(t)Md(It2⊗M→(t))×

(It⊗W[t,t])PRt(It2⊗Md)(It⊗PRt);

(ii)′d是X上的(r,l)-导子当且仅当

MdM→(t)=M⊕(t)M→(t)(It⊗Md)(It2⊗M→(t))×

(It2⊗Md)(It⊗W[t,t])PRt(It⊗PRt);

(iii)′d是X上的导子当且仅当

MdM→(t)=M⊕(t)M→(t)Md(It2⊗M→(t))×

(It⊗W[t,t])PRt(It2⊗Md)(It⊗PRt),

MdM→(t)=M⊕(t)M→(t)(It⊗Md)(It2⊗M→(t))×

(It2⊗Md)(It⊗W[t,t])PRt(It⊗PRt);

(iv)′d是X上的平凡导子当且仅当

证明这里只提供(i)′的详细证明，其他结论类似。定义8(i)中等式的矩阵表示如下：

Md(M→(t)xy)=M⊕(t)(M→(t)(Mdx)y)(M→(t)x(Mdy)),

即

MdM→(t)xy=M⊕(t)M→(t)Md(It2⊗M→(t))xyxMdy。

进一步可得

MdM→(t)xy=M⊕(t)M→(t)Md(It2⊗M→(t))×

(It⊗W[t,t])x2yMdy,

从而

MdM→(t)xy=M⊕(t)M→(t)Md(It2⊗M→(t))×

(It⊗W[t,t])PRtxyMdy,

则有

MdM→(t)xy=M⊕(t)M→(t)Md(It2⊗M→(t))×

(It⊗W[t,t])PRt(It2⊗Md)xy2,

进而有

MdM→(t)xy=M⊕(t)M→(t)Md(It2⊗M→(t))×

(It⊗W[t,t])PRt(It2⊗Md)(It⊗PRt)xy。

由x,y的任意性,则有

MdM→(t)=M⊕(t)M→(t)Md(It2⊗M→(t))×

(It⊗W[t,t])PRt(It2⊗Md)(It⊗PRt)。

故定理5(i)′的条件与定理8(i)的条件等价。证毕。

例7设X={0,a,b,c,1},其中0

(1)

M→(5)=

M⊕(5)=

则由定理1可得(X,→,0)是FI代数，再将结构矩阵M→(5)、M⊕(5)和Md1代入定理5，满足定理5(iii)′的条件，即d1既是X上的(l,r)-导子，又是X上的(r,l)-导子，因此，d1是X上的导子。

例8设X={0,a,b,c,1},在X上定义→的运算表和映射d2:X→X为：

类似地,可以得到M→(5)、Md2和M⊕(5)：

M→(5)=

M⊕(5)=

同样地,将M→(5)代入定理1得到(X,→,0)是FI代数,将M→(5)、M⊕(5)和Md2代入定理5,可知d2是X上的(r,l)-导子,但不是X上的(l,r)-导子,从而不是X上的导子。

引理6[23]设(X,→,0)是FI代数。若d是X上的(l,r)-导子((r,l)-导子或导子),则∀x,yX,有

定理6设(X,→,0)是有限FI代数,且|X|=t<∞。若d是X上的(l,r)-导子((r,l)-导子或导子),则下列性质成立:

证明下面仅给出(iii)′的详细证明。利用偏序关系,可将引理6的(iii)转化为

(d(x)→d(y))→d(x→y)=1。

(2)

M→(t)(M→(t)(Mdx)(Mdy))(Md(M→(t)xy))=

即

进一步可得

从而

(M→(t))2Md(It⊗Md)(It2⊗MdM→(t))×

则有

(M→(t))2Md(It⊗Md)(It2⊗MdM→(t))×

由x、y的任意性,有

(M→(t))2Md(It⊗Md)(It2⊗MdM→(t))×

于是(iii)′得证。证毕

定理7设(X,→,0)是有限FI代数,且|X|=t<∞。若d1,d2,…,dn均是X上的导子,则d=d1·d2·…·dn是X上的导子当且仅当

MdM→(t)=M⊕(t)M→(t)Md(It2⊗M→(t))×

(It⊗W[t,t])PRt(It2⊗Md)(It⊗PRt),

MdM→(t)=M⊕(t)M→(t)(It⊗Md)(It2⊗M→(t))×

(It2⊗Md)(It⊗W[t,t])PRt(It⊗PRt),

其中，Md=Md1·Md2·…·Mdn,Mdi(i=1,2,…,n)为di的结构矩阵。

证明由定理5可得d是X上的导子,则映射d的结构矩阵Md满足定理5(iii)′的条件。又因为d是多个映射复合而成的,可得其结构矩阵Md满足Md=Md1·Md2·…·Mdn,即结论成立。证毕。

5 小结

本文基于矩阵半张量积对有限FI代数的基本性质进行了研究,将有限FI代数上的逻辑表达式转化为逻辑矩阵的简单运算,并以此为基础研究了有限FI代数上的同态与同构,彻底解决了有限FI代数同构的分类问题。同时,有限FI代数上的导子也被用矩阵半张量积方法进行了分析,对于给定有限FI代数上的若干导子,得到了可直接验证各导子复合运算之后是否仍为FI代数上导子的充要条件。