基于综合概率模型与深度学习的智能电网功率-电压映射方法

2022-02-17李建宜李鹏徐晓春施儒昱曾平良夏辉

电力建设 2022年2期

李建宜, 李鹏, 徐晓春, 施儒昱, 曾平良, 夏辉

(1. 华北电力大学电气与电子工程学院，河北省保定市 071003；2. 国网江苏省电力有限公司淮安供电分公司，江苏省淮安市 223400；3. 国网江苏省电力有限公司苏州供电分公司，江苏省苏州市 215000；4.杭州电子科技大学自动化学院，杭州市 310018)

0 引言

近年来随着新能源发电规模日益增大，传统机组提供的电力占比显著减少[1-2]。同时，伴随风机、光伏等分布式新能源、储能以及柔性负荷大量并网，负荷占比不断提升，导致传统配电网逐渐转变为有源系统[3-5]。上述源荷双重特性的变化，对电网的安全特性以及电压控制带来了风险和不确定性。

分布式光伏、风机接入配电网，其不确定性、波动性及间歇性不可避免地会造成配电网节点电压波动频繁[6]。国内外学者针对分布式光伏、风机接入电网后对节点的电压影响展开研究，文献[7-8]针对多地区分布式光伏的中压配电网展开研究，通过标准光伏概率模型生成仿真模型，研究了不同容量光伏、风机接入电网后，配电网电压稳定性分析。文献[9]基于误差前馈法，完成风机集群的超短期快速预测，并考虑不同时间尺度下风电场间的协调互补问题，构建了多时空尺度分层调度模型。文献[10-11]计及分布式电源的不确定性，引入大量小型分布式光伏、风机，利用半不变量法计算概率潮流，从而计算不同节点的电压波动范围，进而验证了区域电网电压节点安全性。文献[12]考虑了风电场之间存在的相关性，采用Copula函数以及K-means聚类方法建立相邻地区风机出力的联合概率模型，然而其在K-means聚类方法上使用试凑法，此方法在处理大量数据时费时费力。上述仿真模型存在以下几点不足：1)光伏、风机模型采用标准概率模型，容易忽略不同地区的光伏、风机出力特性；2)区域内存在多个光伏、风电场时，容易忽略区域内或区域间存在的相关性；3)如采用实际出力数据建立高精度概率模型，既可反映出力特征也可以反映区域间相关性，但数据量过于庞大，极大增加了输入数据的维度，降低了模型仿真效率。

针对以上问题，为了能够较好地反映不同地区新能源出力特征且提高仿真效率，本文首先提出一种融合标准概率模型和实测出力数据的综合概率模型，用于准确构建单个风机、光伏出力特征；然后，结合马尔科夫-蒙特卡洛状态转移模型，对区域内多个光伏及风机的概率模型进行修正，构建考虑多个光伏、风电场相关性的联合概率分布模型；根据此模型生成大量新能源输入数据，通过最优潮流计算节点电压输出数据，通过节点电压标准差验证本模型有效性。最后，为应对数据量庞大这一问题，基于深度学习模型中的PYTORCH框架，建立全连接神经网络进行训练，利用数据深度挖掘高维非线性系统的功率-电压映射关系[13]，并且通过验证数据集准确率验证本方法的有效性。

1 基于马尔科夫-蒙特卡洛模拟的潮流计算

蒙特卡洛法是以概率和统计的理论方法为基础的一种数值计算方法。其原理是将所求问题与概率模型相结合，通过数据离散化对已有概率模型进行合理抽样，从而可以模拟出近似模型。同时，不同地区光伏、风机因地理距离、物理环境因素具有较强的相关性，仅考虑单个节点出力的概率模型会导致整体电网模拟结果与真实分布有较大差异，故通过马尔科夫状态转移模型进行时间-空间的偏差修正，完成联合概率分布模型构建。在此基础上生成电网运行数据集用于深度学习框架训练，流程如图1所示。

图1 功率-电压映射流程Fig.1 Flowchart of power-voltage mapping

1.1 光伏、风机综合概率模型

常规电力系统仿真常用Beta和Weibull两种概率分布模型来模拟光伏、风机实际出力，两种概率模型有着较强的普适性，对于实测数据样本要求不高，但不能够反映光伏、风机的地区出力特征，即实际模拟效果过于理想化，将其在工程上应用会造成较大的功率偏差，从而导致电力系统节点电压偏差较大。而非参数核密度估计本质上是基于数据来生成的一个动态概率密度模型，不同地区间其概率密度可能拥有着较大的差异性，并且不受传统经验或者既定参数影响，故该模型拥有较强的适应性和较高的模拟准确性，可应用于多种运行环境。但该模型计算复杂且基于数据驱动，对于错误数据的敏感度更高，所以对于实测数据样本容错率及数据精度拥有更高的要求。综合考虑上述两种概率模型优缺点，本文提出一种融合传统概率密度和非参数核密度估计的光伏、风机综合概率模型。该方法不仅能够按照实测数据模拟任意随机分布的光伏、风机特性，同时兼顾传统概率分布特征。本文综合概率模型主要流程如图2所示。

图2 光伏、风机综合概率模型建模方法Fig.2 Flowchart of comprehensive probability density modeling of PV and wind

本文综合概率模型建模方法分为以下几个步骤：

1)首先通过最小二乘拟合生成迭代关系，剔除错误数据，然后通过卡方检验判断根据数据抽样形成的概率密度是否符合Beta和Weibull分布规律[14]。通过抽样光伏出力Ps曲线以及风机出力Pw曲线的实测样本进行检验，若检验结果符合传统模型，则通过步骤2)按照传统概率分布即Beta分布及Weibull分布分别建立光伏、风机的概率模型；如检验结果不符合传统概率模型，则根据步骤3)建立光伏、风机的非参数核密度估计模型。其中，光伏、风机数据采用卡方检验，根据检验结果判断实测数据与标准模型拟合度，其拟合度检验公式如下所示：

(1)

2)根据Beta分布及Weibull分布可计算得出光伏、风机的概率密度函数fs(p)以及fw(v)：

(2)

(3)

式中：fs(·)为光伏Beta概率分布模型；α、β均为Beta分布的形状参数；Γ(·)为Gamma函数；p为光伏采样功率；pmax为光伏最大功率；d、q分别为光伏采样区间的首端和末端；fw(·)为风机Weibull概率分布模型；v为风机采样功率；k为Weibull分布的形状参数；c为Weibull分布的尺度参数。

3)根据非参数核密度估计理论，可近似估计fsn(p)以及fwn(v)为：

(4)

(5)

式中：fsn(·)为光伏非参数核密度概率模型；fwn(·)为风机非参数核密度概率模型；ns、nw分别为光伏、风机实测样本编号；h为平滑系数[15]；psi为光伏Beta分布概率密度；pwi为风机Weibull分布概率密度；K(·)为核函数。

4)电力系统负荷一般与用户用电习惯及用电设备的接入与退出相关，对于短时间尺度，其拥有较大的偶然性，对于长时间尺度则随时间变化符合正态分布特征，所以节点i负荷的有功功率概率模型如下：

(6)

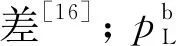
1.2 马尔科夫状态转移矩阵

多光伏、多风电场间存在的相关性受时间-空间多个物理因素影响，其可能与地理位置、天气环境、气温条件等多因素有关，其中存在着极为复杂的深度耦合关系[17]。为简化计算过程且保留场间相关性，认为距离不同的风机存在功率的滞后关系如图3所示。

图3 相邻风机功率滞后示意Fig.3 Power lag diagram of adjacent wind power generators

以风机为例，如图3所示，A地风机与B地风机为相邻风机，且处于同一风场中，两者功率曲线有较强的相似度，不过存在时间上的偏移，而风场是一个混沌系统，无法精确计算任意时刻风速及风向。

故本文通过马尔科夫状态转移方程完成光伏、风机集群的联合概率分布模型，仅考虑光伏、风机功率，设立一个参考点，通过n次采样，计算其与周围风机的功率转移概率，可模拟出其相邻风机此时的出力功率，将转移概率以矩阵形式表示，即可表达为联合概率分布模型，从而达到模拟风电集群的效果。马尔科夫状态转移方程如公式(7)所示。

(7)

式中：P11为马尔科夫状态转移矩阵的标准参考点；P′11为下一状态的P11；ΔPMN表示转移功率差；PMN为采样的第M行第N列光伏或风机功率；M表示光伏或风机行数量；N表示光伏或风机列数量；nsw表示光伏或风机设备总数；Pmax为光伏或风机最大功率；P表示马尔科夫状态转移矩阵。

根据概率转移矩阵，仅需参考点的概率模型，即可计算出同一时刻其他机组功率参数，从而生成光伏、风机集群断面数据。

1.3 蒙特卡洛模拟

通过联合概率分布模型，利用蒙特卡洛模拟生成最优潮流配电网参数进行最优潮流计算[18]，具体计算步骤如下：

1)利用Matpower潮流计算工具，输入配电网网络结构参数、光伏和风机分布类型及参数；

2)根据1.1节和1.2节的联合概率分布模型随机组合生成多组光伏、风机、负荷随机样本，将样本分为两份数据集，一份作为训练深度学习模型输入数据，一份作为验证深度学习训练效果的输入数据；

3)采用牛顿-拉夫逊法依次进行多次确定性的最优潮流计算；

4)统计最优潮流计算所得配电网各节点电压，整理成样本数据，将样本数据分为两份，一份作为训练深度学习模型输出数据，一份作为验证深度学习训练效果的输出数据。

2 基于深度学习的电压-功率映射

功率-电压映射的本质为通过电网运行参数映射得出相对应的电网节点电压数据。虽然样本数据维数较低，但数据量仍较为庞大。其中的非线性关系无法通过常规数学模型来表达，因此利用深度学习网络可快速挖掘数据间的映射关系。深度神经网络相比传统神经网络，其通常分为输入、隐含和输出层，其核心算法思路是通过梯度计算逐层调节神经元权重，进而拟合出复杂模型的非线性映射关系，同时通过反向传播不断更新神经元权重来减小输出误差[19-21]。本文输入为新能源功率及负荷节点功率组成的电网运行参数数据集，输出为节点电压数据集，基于深度学习网络完成的功率-电压映射结构如图4所示。

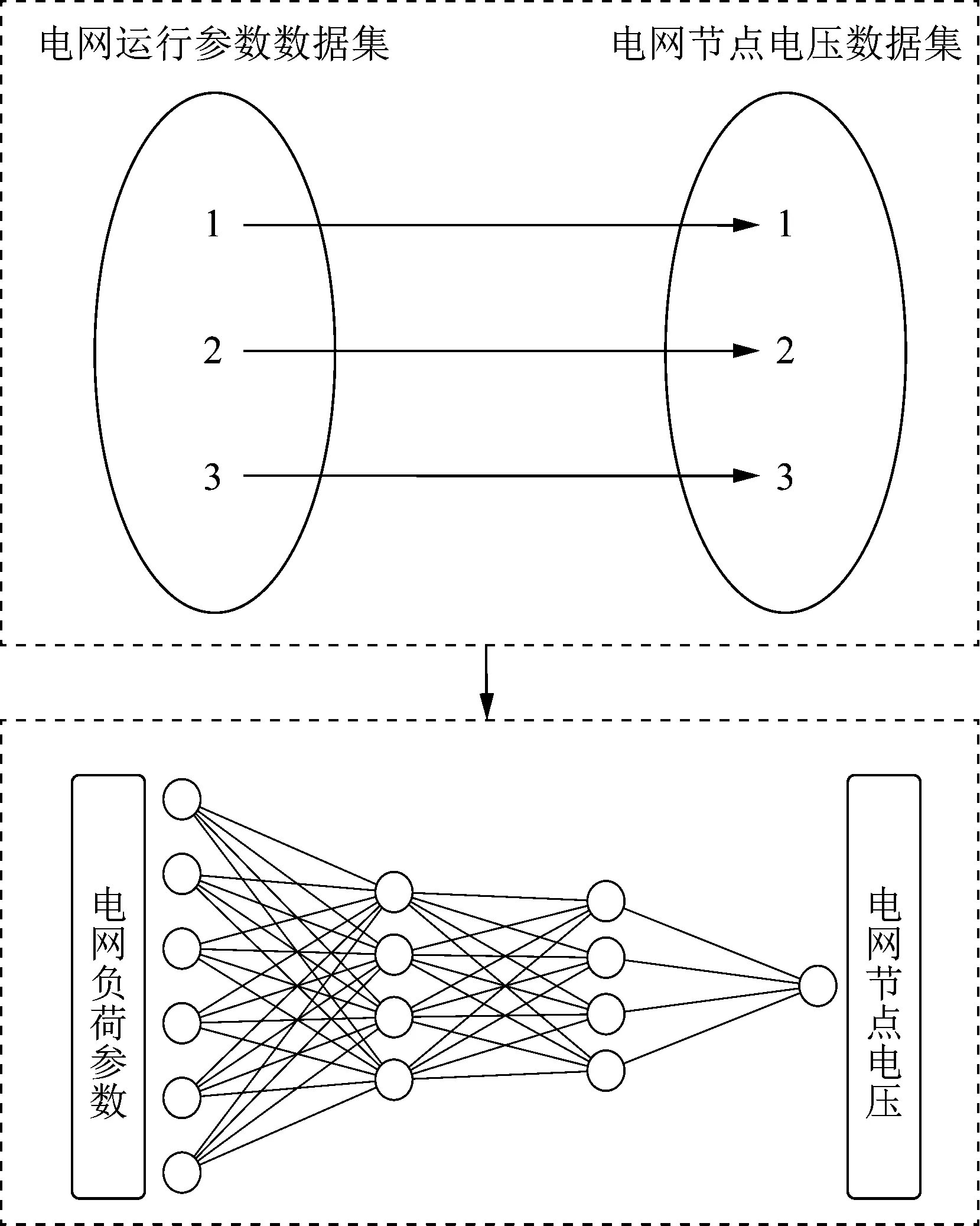
图4 基于深度学习的功率-电压映射方法Fig.4 Power-voltage mapping method based on deep learning

2.1 全连接神经网络框架

(8)

2.2 激活函数及定义误差

激活函数是深度学习中引入非线性因素的主要构成部分。其本身是线性结构，通过每个神经元的不断组合促使整个神经网络逼近非线性模型，从而达到深度神经网络对于功率-电压映射的数据挖掘作用[22-23]。

本文通过sigmoid激活函数来引入非线性关系：

(9)

式中：x为神经网络输入；b0为初始偏置项；b1为修正后偏置项。

将神经网络电压输出值与期望电压存在均方根误差E定义为：

(10)

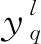
当深度神经网络的输出电压与验证数据集中预期目标电压之间误差小于设定值时，网络结构训练完毕。

3 算例分析

3.1 配电网结构及参数设置

本文采用中国南方某区域配电网进行算例仿真，网络接线如图5所示。

该区域有10 kV、35 kV以及110 kV三个电压等级，同时拥有风机、光伏接入点以及电网分区后的中枢节点，选取本系统中3、7、16、20节点作为风机接入节点，选取其中1、6、9、13、17、19节点作为光伏接入节点；本文采用的光伏、风机位于中国南方某地区配电网，气候较为规律，四季分明。不同季节、天气、时刻发电量存在明显差距但是有周期性规律。故本文选取3月、6月、9月、12月作为特征样本，并从中筛选出多组符合Beta分布的光伏出力数据以及符合Weibull分布的风机出力数据，同时根据卡方检验筛选出多组不符合常规概率分布的出力数据。分别定义光伏接入节点为Ps1、Ps2、Ps3、Ps4，各光伏接入节点参数如表1所示。分别定义风机接入节点为Pw1、Pw2、Pw3、Pw4、Pw5、Pw6，各风机接入节点参数如表2所示。

根据光伏、风机的形状参数以及尺度参数，绘制出传统概率分布下光伏、风机的出力概率密度模型，如图6所示。

图5 配电网拓扑结构Fig.5 Topology of distribution network

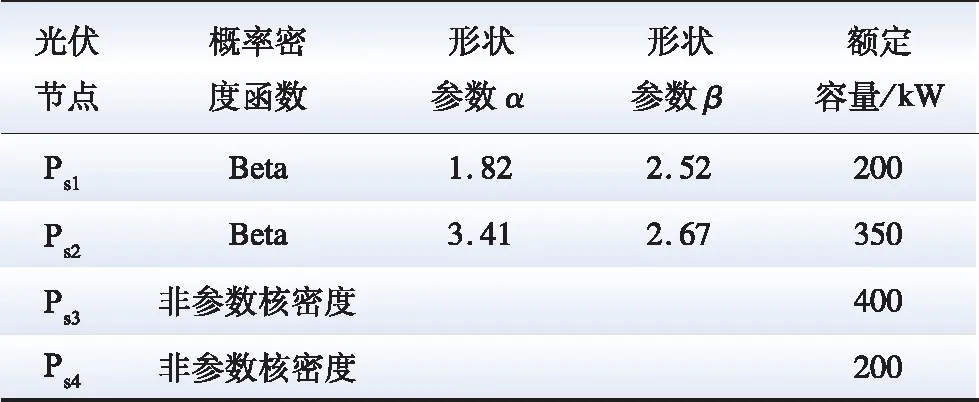
表1 光伏接入点参数Table 1 Parameters of photovoltaic access nodes

表2 风机接入点参数Table 2 Parameters of wind power access nodes

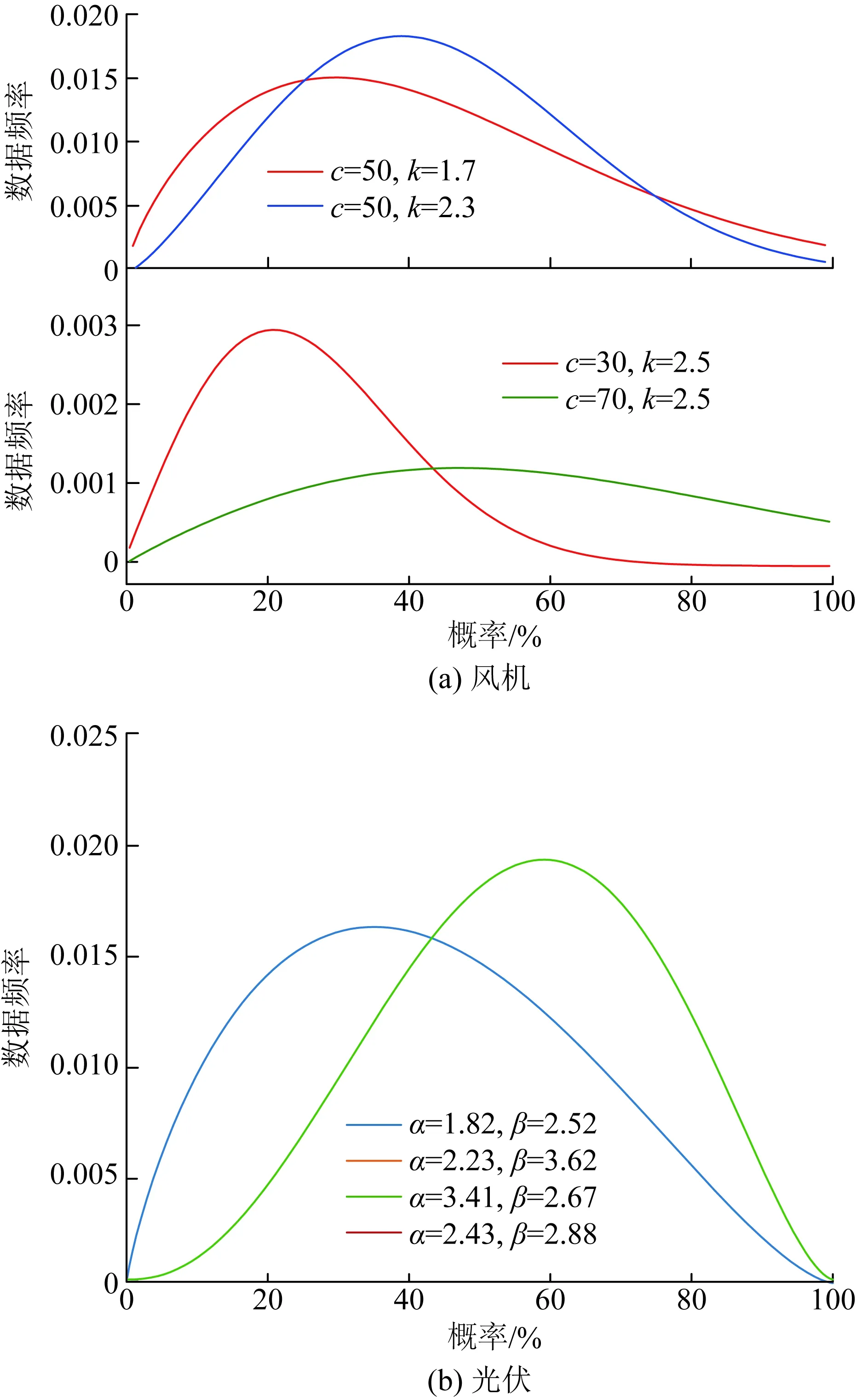
图6 概率密度模型Fig.6 Probability density model

图6(a)和图6(b)分别表示不同尺度参数以及形状参数下风机和光伏的标准概率密度模型，也是本文实验数据经卡方检验后，较为符合的几种概率模型。

经过χ2检验可知，接入节点7、20的Ps3、Ps4不符合Beta分布，接入节点13、19的Pw5、Pw6不符合Weibull分布，故采用非参数核密度估计模型；其他配电网负荷节点服从正态分布规律，取均值为节点负荷的稳态值，波动范围为±5%。

3.2 潮流准确性验证

基于配电网系统，采用本文概率密度模型进行蒙特卡洛抽样，利用Matpower工具进行8 000次最优潮流计算。

图7为本文概率密度模型以及常规概率密度模型抽样进行最优潮流后的结果准确度。其中，本文选取了2、18、19号节点作为试验对象，计算其标准概率密度模型下的节点电压标准差以及本文综合概率密度模型下的节点电压标准差。

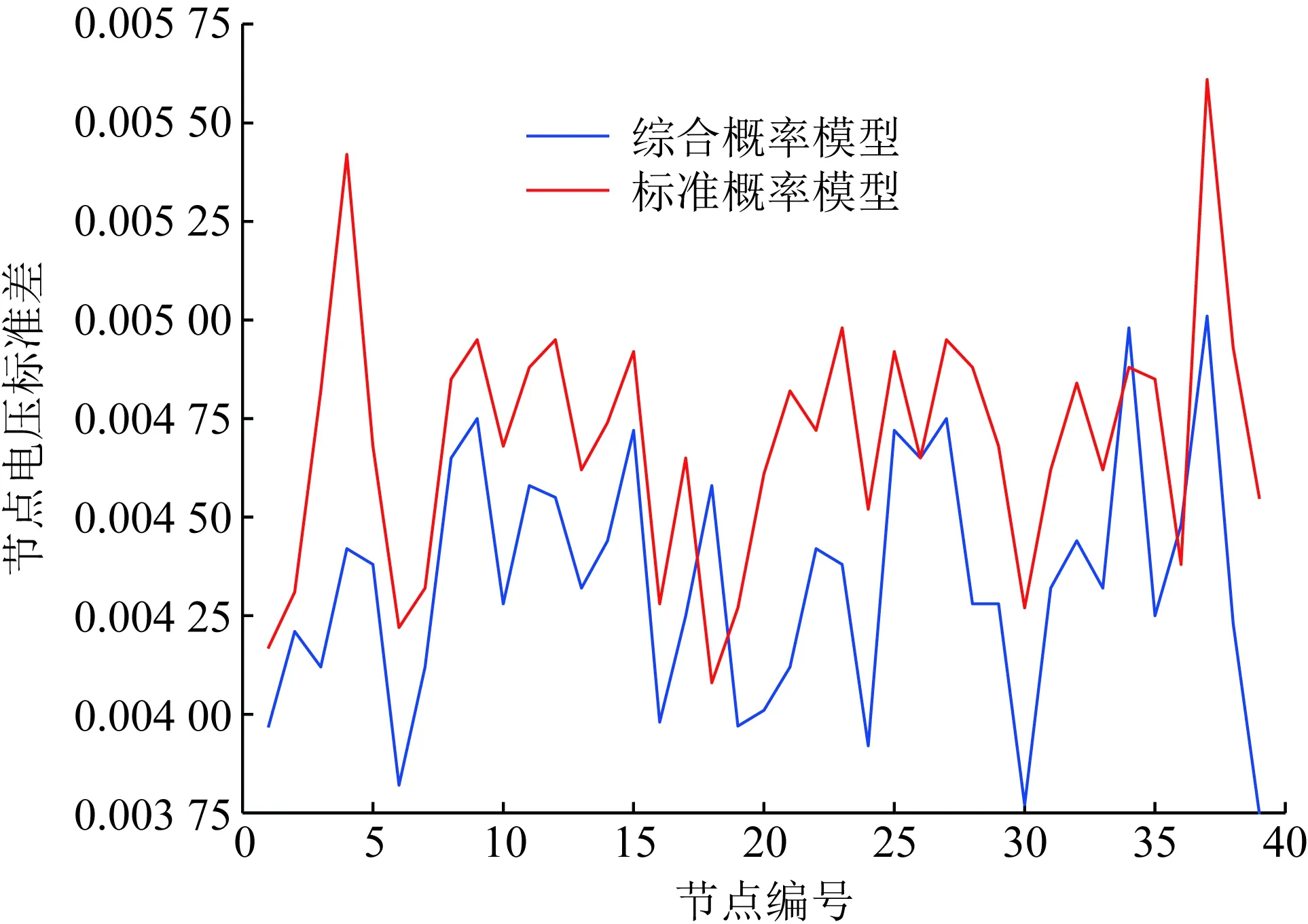
图7 节点电压标准差Fig.7 Standard deviation of node voltages

如图7所示，通过对比多个节点的电压标准差，基于综合概率密度模型进行的最优潮流计算，节点电压标准差控制在0.004，相较于标准概率模型的0.005，电压标准差更小。说明本文提出的综合概率模型具有更高的精度以及更小的误差，可用于深度学习训练。

3.3 训练深度学习模型

整合3.2节根据概率模型生成的8 000组数据及最优潮流计算结果生成深度学习模型所需数据集，其中选取5 000组数据作为验证数据集，其余3 000组数据用于训练模型。利用PYTORCH框架搭建全连接神经网络，层数设定为5，每层神经元数量分别为39、72、144、72、39。设置训练循环次数为2 000次，每次反向传播对神经元权重进行微调整。训练过程如图8所示。