基于相变与悬链线连续相位调控的超构光子开关
2022-02-17宋睿睿邓钦玲周绍林
宋睿睿 邓钦玲 周绍林†
1) (华南理工大学微电子学院,广州 510640)
2) (琶洲实验室,广州 510335)
针对超表面相位调控中的无源及离散特性,本文拟将等宽悬链线超构单元与非易失性相变介质结合,探索研究一种高效连续相位调制的双稳态相变有源波前超构开关.首先在9—10 µm之间的宽带中红外波段实现了可动态切换的波前偏转开关;当相变层在非晶态和晶态之间切换时,入射光波前分别呈现异常反射和正常的镜面反射,即“开”或“关”两个偏转状态.其次展示了一种可动态切换的高阶贝塞尔光束开关:非晶态时,9.6 µm波长垂直入射下交叉极化转换效率接近100%,产生正常的几何相位调控与二阶贝塞尔聚焦,即“开”态;而相变至晶态时,交叉极化与几何相位调控被“关”闭.本质上,自旋-轨道相互作用具有无色散的相位调控保证了该类器件的宽波段工作特性,在未来的有源光电子集成、光通讯等应用领域中具有重大潜力.
1 引言
截止目前,多功能高效电磁控制仍然是一个永恒的话题,涵盖从可见光到微波以下的波段.作为平面或二维(2D)超材料,超表面具有深亚波长厚度,近十年来几乎应用于任意电磁调控中,其超薄特性有利于紧凑架构的光电集成.与传统光子器件不同,超表面旨在通过周期性或随机分布的亚波长亚原子,例如纳米棒、纳米光栅、纳米梯形、悬链线、LC谐振单元、开口谐振环等,以逐像素的方式调节入射光振幅、相位和偏振态,引入可控的局部相位与振幅突变,取代传统方法通过3D分布调节传输相位[1].已报道的各类平面纳光子器件涵盖可见光到太赫兹波段,如贝塞尔光束发生器[2−5]、全息超表面[6−9]和超透镜[10−12]等.特别是由于局部突变相位,在亚波长尺度上实现了相位分布的任意控制.在基于共振相互作用的传统等离子体超表面中[13−15],所产生的相位延迟高度色散.为了获得无色散的相位调制,各向异性元件中的偏振转换得到广泛研究,例如众所周知的Pancharatnam-Berry(P-B)相位[16,17].基于几何相位的超构器件可以实现灵活和多功能的波前调控,但仍然存在一些可解决的问题.
首先是器件的无源特性,导致其缺乏可重构或动态调控机制.因此,人们在超表面基础上引入有源介质材料或动态调控机制,实现有源的多功能光子器件,如微电子机械系统(MEMS)[18]、二维材料(如石墨烯[19]、二硫化钼(MoS2)[20]等)、液晶[21]、半导体[22]和相变材料[23,24]等.其中,硫系化合物是一种很有前景的相变材料,尤其是其非易失性、便于工艺集成等优势,为新型有源光子器件提供了有效途径.具体来说,GeSbTe合金作为一种典型的相变材料已经在光盘存储中使用了多年[25,26],最近广泛用于构建可重构光子器件[27−29].GeSbTe合金可以通过适当的电[30]、光[31]或热[32]等激励在非晶态、晶态及中间状态间可逆切换.此外,由于状态之间的高折射率对比度以及近中红外光谱范围内的低损耗,GeSbTe合金是可重构器件的理想材料,如动态全息[33]、菲涅耳波带片[34]、超透镜[35,36].
其次,根据衍射理论[37],有限且不连续的空间相位采样对于大角度均匀偏折或光弯曲是一个巨大的挑战.为了克服离散超构单元的限制,一些新型结构广泛用于宽光谱范围内的连续相位调控,如金属或介质悬链线结构[38−40],尽管目前相位和振幅响应还不够理想、效率较低[41].近年来,拓扑优化作为一种提高连续结构性能的有效手段[42],尽管数值计算工作量较大,但可实现周期结构或小面积器件.最近,张飞等[43]基于优化悬链线提出了一种宽频带、高效率、超广角波前的全介质光学超表面及其相位流水线优化设计策略.
本文旨结合基于相变的有源控制与悬链线连续相位调控,构造了基于Ge2Sb2Te5-悬链线混合超构单元连续波前调制的有源超表面相位开关,分别实现光束偏转和高阶(拓扑电荷数l=2)贝塞尔光束动态切换.在基于Ge2Sb2Te5的超构集成单元中,利用几何相位与传输相位实现动态波前调控.Ge2Sb2Te5处于非晶态时,交叉极化与异常反射被“打开”,在9—10 µm波段内平均效率达80%.当Ge2Sb2Te5转变为晶态时,异常反射几乎被“关闭”,仅产生正常的镜面反射,即实现光束偏转的“开”和“关”态.进一步,展示了一种高阶(l=2)贝塞尔光束开关器件.特别地,在9.6 µm波长处,非晶态下的器件极化转换效率(PCR)接近100%.相关结果为光电集成、波前重构等应用提供了新的有源集成光调控思路.
2 基本原理
2.1 线宽渐变悬链线连续波前调控
悬链线光学是近年来亚波长光学和电磁学中一个新兴的研究点,在最近的一篇综述中介绍了其历史、理论和应用[44].作为一种连续波前或相位调控超构单元,如图1(a)所示,可优化流水线型悬链线[43]设计,实现9.6 µm入射时沿–x方向光偏转最大至40°,沿x轴方向的相位分布应为 2πx/Λ,其中Λ9.6/sin(40°) 是横向排列周期,曲线轨迹可以用“等强度悬链线”[38]表示为
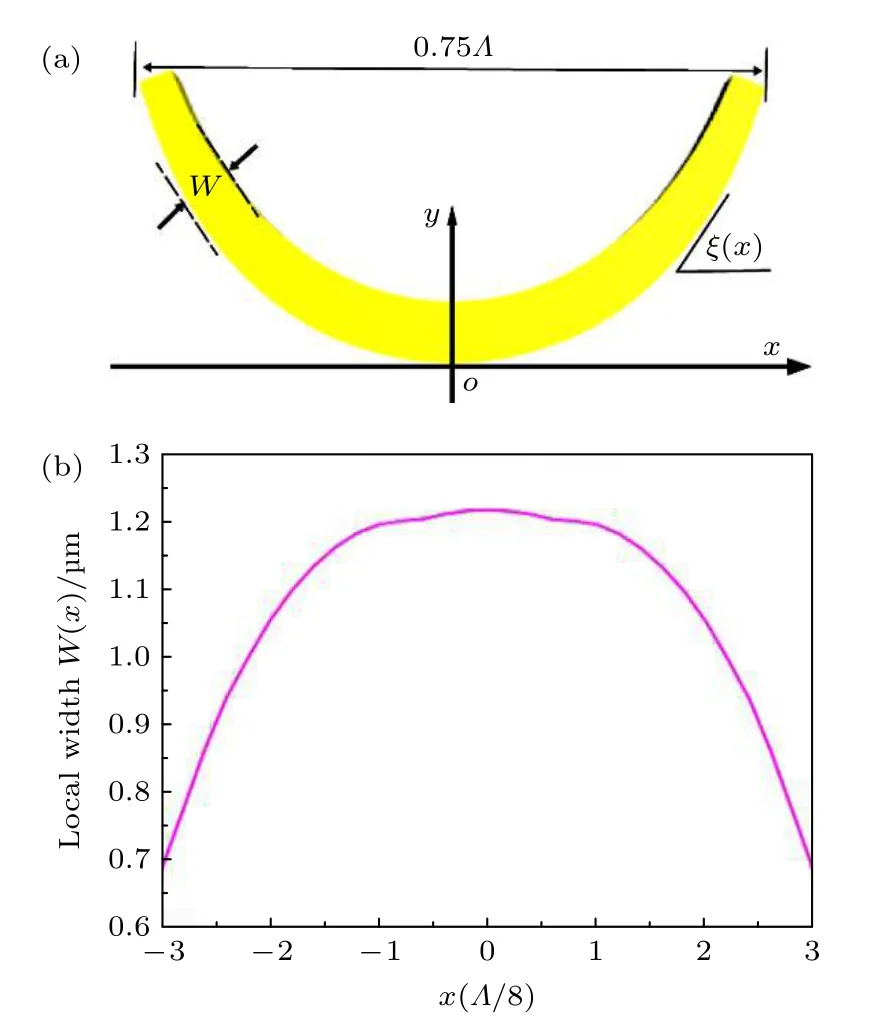
图1 优化后的悬链线特征[43] (a) 水平长度为0.75 Λ的单个悬链线结构;(b)经流水线优化算法得到的悬链线局部宽度W(x)随x的变化Fig.1.Schematic of the catenary atom[43]:(a) Single catenary structure with a horizontal length of 0.75 Λ;(b) the locally varied width W(x) of the catenary by streamlined optimization algorithm along x-axis.
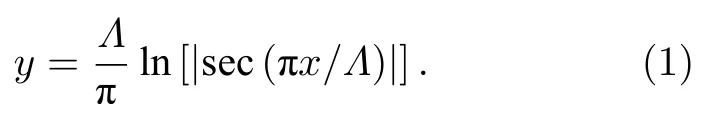
当x±Λ/2 时,y值趋于无穷大,曲线两端由一个截断系数f=0.375决定,因此,光学悬链线的水平跨度为(−fΛ/2,fΛ/2).
沿悬链线切线方向与x轴的倾角ξ(x)从−π/2到 π/2 在左右端点之间变化,根据几何相位关系,将产生连续、局域的几何相位Φ(x)2σξ(x),其中σ=±1 表示左旋和右旋圆极化(分别为LCP和RCP)入射光.其中,倾角ξ(x)可以表示为
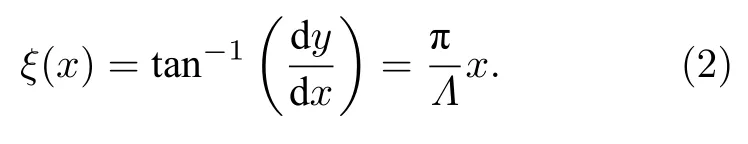
因此,沿悬链线产生的几何相位分布(调制)可以写成
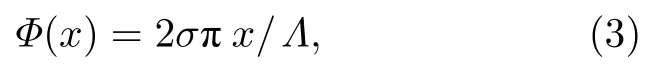
即沿着x轴的线性相位梯度为 2π/Λ,相当于等效的局域单向波矢量[45].进一步,通过调节悬链线周期Λ和垂直于悬链线切线方向的线宽W(x)变化,可优化单向局域等效波矢分量对应的局域场分布、波前偏转.经过优化,本次拟采用线宽W(x)随x轴变化关系,如图1(b)所示[43]的悬链线单元.
2.2 基于悬链线单元的几何相位调控原理分析
几何相位,又称为Pancharatnam-Berry(P-B)相位[16,17],一般产生于圆偏振光与等离子体或谐振单元相互作用的交叉偏振(或极化)分量中,其值为φ=2ξ,其中ξ是单元结构的平面内取向角,如图2(a)所示.根据单元结构排列方式的不同,几何相位调控方式可以直观地分为两类,即生成离散几何相位和连续几何相位.一般来说,离散几何相位是从离散排列的单元结构中获得,如同对波前在亚波长尺度进行离散采样;连续几何相位,则由具有空间上连续相位调控模式的谐振结构产生,例如本文的悬链线原子,如图2(b)中所示.改变悬链线排布方式,可对入射光实现特定的连续波前调控,如本文展示的异常偏折与贝塞尔光束.
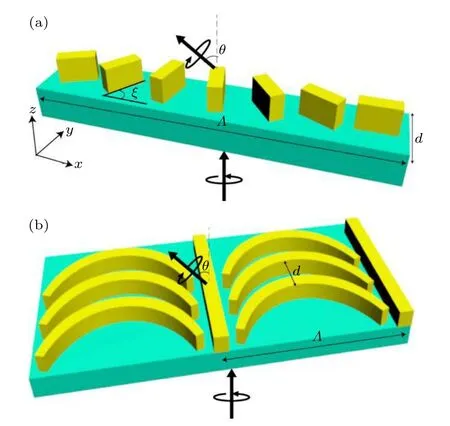
图2 (a)离散几何相位实现异常偏折;(b)连续几何相位实现异常偏折Fig.2.(a) Discrete geometric phase for abnormal deflection;(b) continuous geometric phase for abnormal deflection.
首先,异常光束偏折或折射,需产生线性相位分布φ(x)或常数梯度dφ(r)/dx,
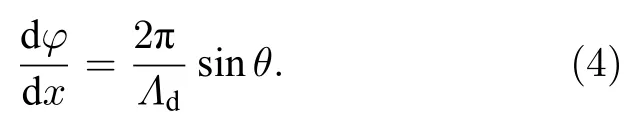
根据广义折反射定律[13],(4)式可理解为所有子波前,在设计波长λd下以相同的角度θ出射,如图2所示.形成的沿着x方向相位梯度为 2π/Λ,折射角为θ,满足公式θ=arcsin(λd/Λ).
为了实现零阶贝塞尔光束,需要产生径向的线性相位分布φ(r),

对(5)式两边积分,并且代入r(y2+x2)1/2可得
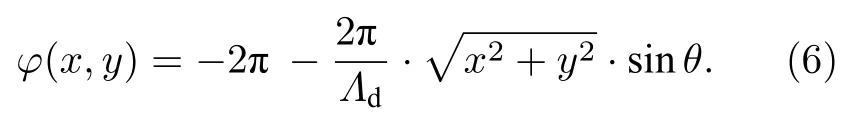
在此基础上,如需产生高阶贝塞尔光束,需要添加沿角向(或弧向)的额外相位nφ,这里φ=tan−1(y/x),表示xoy面内的弧向方位角,即引入涡旋相位后
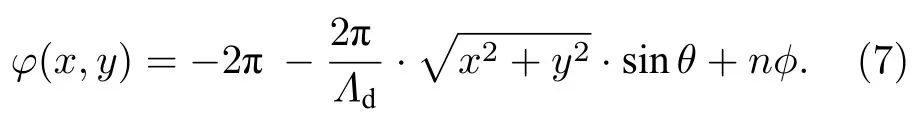
因此,针对特定波前调控,如贝塞尔光束生成,与线性相位决定的波前偏转类似,需产生圆对称的螺旋或同心相位分布.具体地,悬链线可以在极坐标系中排列,便于同时实现沿径向、角向的相位调控.如图2(b)所示,单元结构两端的相位差为±2π,可单个结构直接形成梯度为 2π/Λ的线性相位调控.对于悬链线的同心圆排列,将沿径向直接产生梯度为 2π/Λ的线性相位分布,且与位于相同半径圆上的悬链线端点对应的参考相位krr(kr表示径向波矢量)一致;同时,沿角向(或弧向)悬链线逐渐旋转,将进一步在相应转角φ处引入2倍于转角的几何相位2φ.因此,其综合相位分布呈现螺旋分布(见图3(d)),旋转一周引起相位变化为4π,形成贝塞尔分布阶数或涡旋光拓扑电荷数l=2.
类似地,对于悬链线的螺旋排列,如产生l=0的零阶贝塞尔分布,即相位呈现同心圆分布,需悬链线端点对应的参考相位krr引入附加相位krr=–2φ(即(7)式中n=–2),进而与悬链线沿角向旋转产生的几何相位2φ抵消,产生所述的同心圆分布(见图3(c)).因此,综上分析,悬链线端点的轨迹满足[46]
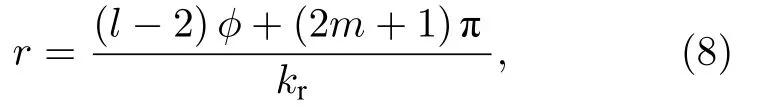
式中,l为拓扑电荷数或贝塞尔分布阶数,m=1,2,3···表示初始相位.图3(a)为l=0的贝塞尔光束设计分布,即悬链线双螺旋排列;图3(b)为l=2的贝塞尔光束设计分布,悬链线同心排列;图3(c),(d)分别展示了图3(a),(b)中设计的相位分布.悬链线的其他排列具有不同的轨道角动量[38].值得注意的是,该设计可以超越离散的亚波长光栅结构限制,形成理想的复杂相位分布[40].
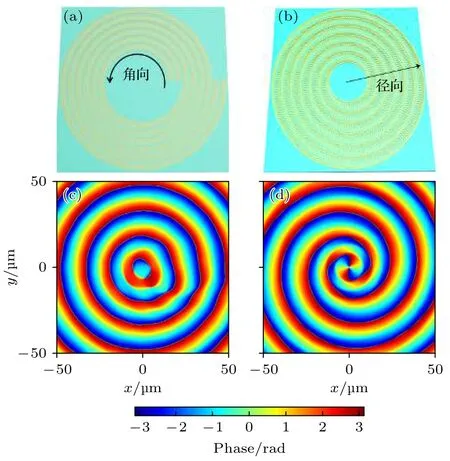
图3 (a)基于螺旋悬链线排列的零阶贝塞尔光束发生器(l=0);(b) 基于同心圆悬链线排列的高阶贝塞尔光束发生器(l=2);(c) 9.6 µm右旋圆光垂直入射图(a)中结构得到的相位分布图;(d) 9.6 µm左旋圆光垂直入射图(b)所示结构得到的相位分布图Fig.3.(a) The zero-order Bessel beam generator based on spiral catenary arrangement (l=0);(b) high-order Bessel beam generator based on concentric circular catenary arrangement (l=2);(c) phase distribution for the arrangement in (a) at the incidence of 9.6 µm RCP waves;(d) phase distribution for the arrangement in (b) at the incidence of 9.6 µm LCP waves.
2.3 基于相变集成的有源超构开关
基于悬链线单元的几何相位调控效率,决定于整体器件的交叉极化效率.为了提高交叉极化分量的能量转换效率,本次拟采用反射模式的金属-绝缘层-金属(MIM)优化单元模型.如图4(a)所示,绝缘体层由Ge2Sb2Te5和MgF2薄膜组成,夹在金衬底和金悬链线阵列之间.Ge2Sb2Te5薄膜作为有源介质,可动态调节不同状态实现超表面动态相位调制,如光束偏转.在Ge2Sb2Te5表面沉积MgF2薄膜作为氧化缓冲层.同时,MgF2层用作高折射率Ge2Sb2Te5和空气之间的折射率匹配层,以保证在给定波长处较高的交叉极化效率.如图4(b)所示,悬链线超构单元具有相同尺寸,同时被截断的悬链线水平跨度为0.75Λ.为保证相位连续性和振幅均匀性,在截断区域增加宽度为w1的垂直结构,且沿y方向两个悬链线原子的间隔设置为d.
作为有源调控机制,将Ge2Sb2Te5薄膜引入MIM结构,便于引入基于相变的附加传输相位调控.以波前偏转为例,超表面产生的相位分布直接决定了器件的水平波矢[14,47],如图4(c)所示,沿悬链线x方向不同位置处得到反射波(x分量)的相位突变分布.显然,在右旋RCP平面波正入射下,Ge2Sb2Te5非晶态时悬链线在一个周期或一列中产生从0到2π的线性相移,进而产生由常数相位梯度或波矢决定的反射平面波.这种整体范围连续的相移,使得异常偏转效率高于那些通过离散单元结构引入的不连续相位采样效率,与先前报道结果预测一致[43].然而,如图4(d)所示,Ge2Sb2Te5相变至晶态时,仅在给定波长(如9.6 µm)附近产生振幅极小的交叉极化分量,剩下以共极化为主导的正常镜面反射,因此几乎不能产生有效的几何相调控.通过优化提取Ge2Sb2Te5两种状态下x-z平面强度分布,可直观描述有源相位调控与波前偏转机制.以9.6 µm垂直入射为例,结果如图4(e),(f)所示,非晶态时(图4(e)) F-P模式表现出局域增强的电场分布,并与悬链线结构有效地耦合,产生图4(c)中覆盖[0,2π]的全范围的线性几何相位,进而产生由常数相位梯度决定的定向波前偏转.晶态时(图4(f))工作在非共振模式,几乎没有局域场耦合,因而交叉极化和几何相位调制幅度几乎可忽略.
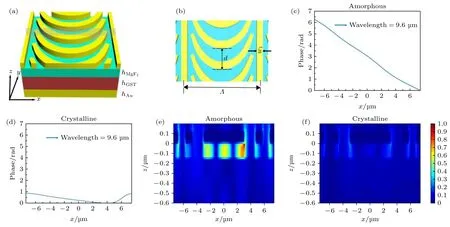
图4 悬链线结构单元模型及其特性 (a) 悬链线结构单元横截面图;(b) 前视图;(c) 9.6 µm处非晶态和 (d)晶态沿位置x的相位变化;(e) 9.6µm处非晶态和(f)晶态归一化横截面强度分布Fig.4.A catenary-based atom and its characteristic:(a) The cross-sectional view;(b) the top view of one atom.The phase change with respect to position x (c) in the amorphous state and (d) the crystalline state at 9.6 µm.The normalized cross-sectional intensity distribution at 9.6 µm in (e) amorphous and (f) crystalline states.
3 结果与讨论
3.1 动态波前偏转控制
为验证上述主动波前控制方法的可行性,用有限时域差分法(FDTD)对MIM单元模型进行了数值计算.首先,如图5(a)所示,建立了用于宽带线性相位调制的悬链线-Ge2Sb2Te5偏转混合模型.沿x轴和y轴使用周期边界条件,沿z轴使用完美匹配层.其中,相变介质Ge2Sb2Te5厚度hGST=0.6 µm,以确保在热或电刺激下发生可逆相变,同时保证足够厚度实现的F-P模式的正常关闭.其次,选择合适厚度的二氟化镁hMgF2=0.15 µm阻挡空气与Ge2Sb2Te5接触.悬链线足够薄(hAu=0.12 µm)以便于制造、减小计算量.Ge2Sb2Te5的光学常数采用文献[48]中的数值.特别地,在工作波长9.6 µm处非晶态的折射率为3.46,晶态的折射率为4.92+i0.17.如图4(b)所示,悬链线在x方向上的周期为0.75Λ=11.14 µm,在y方向上的间距为d=3.5 µm.

图5 可切换的超构阵列偏折器件 (a) 基于悬链线-Ge2Sb2Te5集成的有源波束控制准连续超表面;(b) 非晶态共偏振和交叉偏振反射率的仿真结果;(c) 极化转换效率(PCR)谱;(d) 非晶态和 (e) 晶态下9.0 µm,9.5 µm和10.0 µm波长光束以不同偏折角反射;(f) 非晶态和 (g) 晶态下9 µm右旋光入射时x-z平面内的反射电场(Ex)归一化振幅分布Fig.5.The switchable meta-array for deflectable devices.(a) The Catenary-Ge2Sb2Te5 integrated quasi-continuous metasurface for active beam control.(b) The simulated results of the co-polarized and cross-polarized reflectivity in the amorphous state.(c) Polarization conversion efficiency (PCR) spectrum.The beams with different wavelengths of 9.0,9.5 µm,and 10.0 µm are reflected/deflected to distinctly different angles in the (d) amorphous state and (e) crystalline state.The normalized amplitude distribution of the reflected electric field (Ex) for RCP incidence (9 µm) in the (f) amorphous and (g) crystalline state in the x-z plane.
如图5(b)所示,在9—10 µm的宽光谱范围内,在非晶态下整体反射率由交叉极化分量(>75%)主导,而共极化反射率被抑制(<10%).特别地,定义并计算了极化转换比PCR(PCR=Rcross/(Rcross+Rco))来表征交叉极化效率.图5(c)显示了两种状态下波长的仿真PCR谱.结果表明,在9 —10 µm的宽带光谱范围内,非晶态的PCR大于90%,晶态的PCR小于20%,并且在9.6 µm处,非晶态下极化转换效率接近100%.此外,图5(d),(e)分别给出了两种状态下不同波长不同角度相关的强度分布.显然,在非晶态中,交叉极化被“打开”,产生异常偏转(或反射),而在晶态中偏转被“关闭”(只有镜面反射).值得注意的是,如图5(f),(g)所示,在9.6 µm入射时,非晶态下,观察电场分布可知,光束向39.5°的角度异常反射,与θsin−1(λ/Λ) 的理论值40.27°基本一致;而在晶态时,几乎为镜面反射,这与图5(d),(e)结果一致.
3.2 高阶贝塞尔光开关
根据解析设计,在仿真中制作了拓扑电荷数l=2的高阶贝塞尔光束发生器.基底金膜厚度为120 nm,l=2主视图图像如图6(a)所示.所有样品径向周期Λ均为14.85 µm,由kr2π/Λ确定衍射光束的径向波矢量.r1=30.0 µm,r2=119.1 µm.图6(b)为图6(a)的局部放大图,这样的排布方式会在径向产生关于中心对称的线性相位分布,并在弧向产生对应的涡旋相位分布,进而产生高阶贝塞尔光束[49].非晶态下,9.6 µm波长的右旋圆极化垂直入射时,得到的高阶贝塞尔光束的x-z场分布,如图6(c)所示.特别地,高阶贝塞尔光束的特点是中心空心,携带典型的轨道角动量.如图6(d),(e)所示,对于相同的径向波矢量和波长,光斑尺寸(定义为贝塞尔光束最内环的半径)随拓扑电荷数l增加而变大.同时,还可以通过改变微/亚微尺度光栅的周期Λ来控制光斑大小.减小Λ值后,贝塞尔光束光斑半径可达到亚波长量级,这是传统空间光调制器(SLM)器无法实现的[46].如图6(f)所示,从非晶态至晶态相变时,高阶贝塞尔光束被“关闭”,对应聚焦分布消失.超高效率贝塞尔光束使非晶态(最大)和晶态间产生较大的汇聚光强对比,对于大开关比的有源光子器件非常理想.
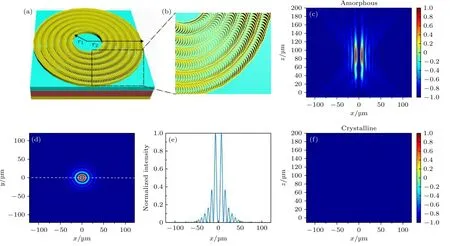
图6 可切换高阶贝塞尔光束器件 (l=2) (a) 具有同心悬链线排列的可切换高阶贝塞尔光束发生器(l=2)及(b)局部放大图;(c)非晶态下x-z平面 (y=0) 内归一化强度分布;(d) x-y平面 (z=100 µm)的归一化强度分布;(e) 沿图(d)中虚线的归一化强度;(f) Ge2Sb2Te5晶态下x-z平面 (y=0) 内归一化强度分布Fig.6.The switchable high-order Bessel beam device (l=2):(a) The switchable high-order Bessel beam generator with concentric catenary atoms (l=2) and (b) its partially enlarged view;(c) the normalized intensity distribution in the x-z plane (y=0) in the amorphous state;(d) the normalized intensity distribution in the x-y plane (z=100 µm);(e) the normalized intensity along the dotted line marked in (d);(f) the normalized intensity distribution in the x-z plane (y=0) in the crystalline state of Ge2Sb2Te5.
4 结论
综上所述,本文通过提出基于悬链线连续相位调控和Ge2Sb2Te5相变相结合的MIM有源波前调控光子开关器件,揭示了一种相位可动态重构和连续相位调控超表面的应用潜力.首先通过一维排列的悬链线单元生成线性相位分布并实现了光束偏转开关或动态切换.在从非晶态到晶态的相变过程中,反射波可以在一个特殊的异常反射角与正常的镜面反射之间“打开”或“关闭”.其次,通过同心圆排列的悬链线单元展示了携带轨道角动量的贝塞尔光束开关.在非晶态下,该器件被“打开”,产生具有优化前向传播的高阶贝塞尔光束.当相变至晶态时,贝塞尔光束完全“关闭”,没有正向传播.因此,希望本文所提出的方案可以为构建相位型光子开关等有源光器件提供切实可行的参考.
