随机风场中系留无人机系统运动响应研究
2022-02-17邢龙涛冯志壮刘晨李贞坤
邢龙涛,冯志壮,刘晨,李贞坤
(中国直升机设计研究所 直升机旋翼动力学重点实验室,江西景德镇,333001)
系留无人机系统由多旋翼无人机、综合缆绳、系缆收放系统组成,具有续航时间长,抗干扰能力强等优点。系留无人机系统在运动过程中会受到随机风作用,随机风荷载会使系留无人机系统发生剧烈运动,严重影响系留无人系统的稳定性。所以需要对系留无人机系统的运动响应进行研究。有些学者对平均风场中系留无人机系统的运动响应进行了研究。Sina Doroudgar[1]通过拉格朗日方法建立了系缆的运动方程,研究了平均风场中系留无人机系统的静态和动态运动。
王亚伟等[2]采用ADAMS软件对飞艇系留系统进行了静力学与动力学仿真,将缆索结构处理成质点-弹簧-阻尼系统,计算得到8个静力学工况和1个动力学工况下系缆张力变化情况,得到飞艇攻角、线密度对系缆静态构型的影响和风速对系缆张力的影响。方治华和李晨[3]将模拟的随机风荷载导入到斜拉索表面,计算拉索在自然风作用下的振动响应。柯世堂,王同光和曹九发等[4]采用谐波叠加法模拟塔架和风轮的来流风速时程,然后对海上风力发电系统结构进行风振动力响应和风振系数计算。刘小会等[5]研究了随机风场中覆冰四分裂输电导线的舞动问题。杨庆山和沈世钊[6]等利用随机振动离散分析方法计算随机风振响应,并对悬索结构随机风中响应进行了参数分析。杜齐鲁[7]等对随机风作用下系泊浮体系缆力进行了研究。基于Davenport谱和API谱得到随机风速时程,给出了不同载态情况下系缆力的模拟公式及其参数值。
本文建立了张紧状态下系留无人机系统的运动方程,并对系统进行模态分析,采用伽辽金法对张紧状态下系留无人机系统运动方程进行离散化处理,基于Davenport脉动风谱,采用谐波叠加法模拟随机风,研究了随机风荷载作用下,对不同位置处系缆法向运动响应进行了分析。
1 张紧状态下系留无人机系统运动方程
假设系留缆绳满足弹性本构关系,忽略弯曲剪切和扭转刚度。系留无人机系统的简图如图1所示,其中xOy为惯性坐标系,V为风速,Si为静态构型,St为动态构型,e1和e2分别是切向和法向的方向向量,忽略副法向方向的运动,动态位移U可沿e1、e2方向分解为U1、U2。系留缆绳的运动微分方程为[8]:
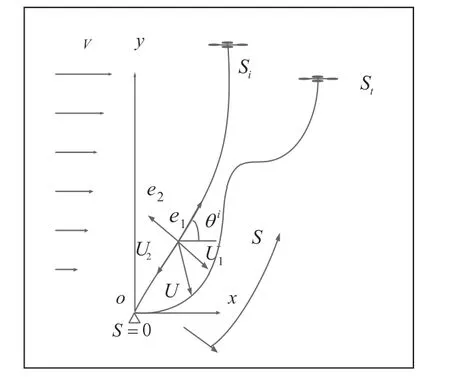
图1 系留无人机运动简图
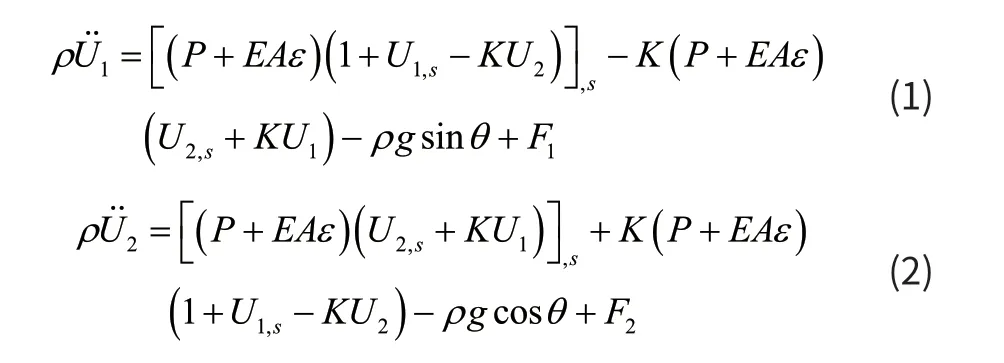
其中:P为静态张力,K为静态曲率,E为系留缆绳的弹性模量,A为系留缆绳的横截面积,θi为平衡构型中缆绳切向与水平方向的夹角,ρ为缆绳线密度,g为重力加速度,F1和F2分别为系留缆绳在切向和法向上所受的风荷载,由于F1很小所以忽略。
在S=L处系缆与无人机质心铰接,无人机所受力都作用在质心处,无人机的受力图如图2所示。

图2 无人机受力简图
其中:F为无人机的电机驱动力,Mg为无人机的重力,Pt(L) =P(L)+EAε为系缆的总拉力,FDx是无人机在水平方向上所受的气动力,其表达式为:
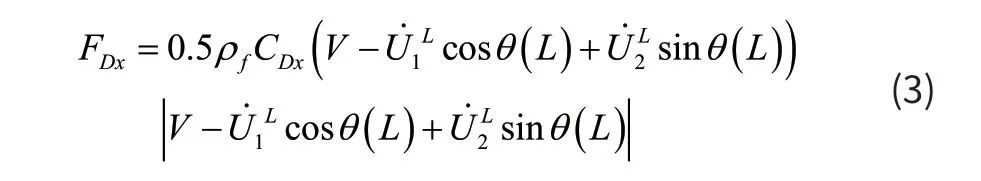
缆绳下端点铰接,将系缆上端点所受各力沿e1和e2方向进行分解,系留无人机系统的边界条件为:

为了下面的计算方便,对系留无人机系统的运动方程进行无量纲化处理,其表达式为
由于缆绳质量很小,而无人机质量很大,当系缆处于张紧状态时,系缆动张力变化很小,因此系缆切向可以应用准静态拉伸理论,所以用平均动应变来表示系缆各点的动应变。由于系留无人机系统平衡状态是处于均匀风场中,系缆受气动力作用使系缆有构型,所以平衡曲率不为0,但是平衡曲率k很小,可以当成小量处理,保留运动方程和边界条件中平衡曲率的一次项。因此系缆的运动方程和边界条件变成:
系缆法向运动方程:
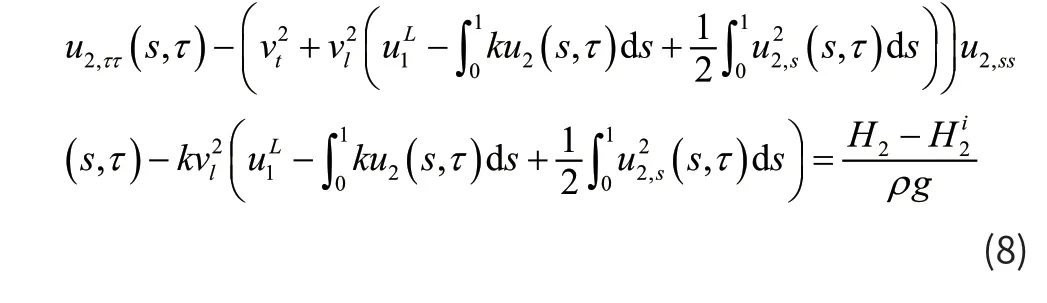
边界条件为:

2 模态分析
忽略方程(8)到方程(11)中的非线性项得到:
系缆法向线性化方程:

边界条件:
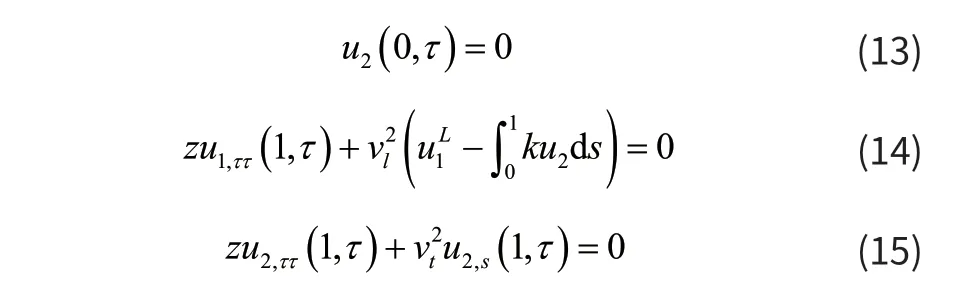
运用变量分离设解为:
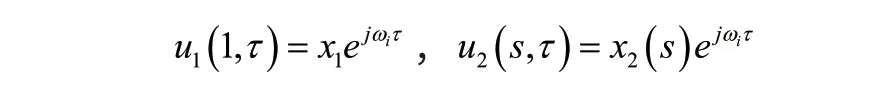
将上式代入到线性化方程和边界条件中整理得到系缆法向频率方程为:
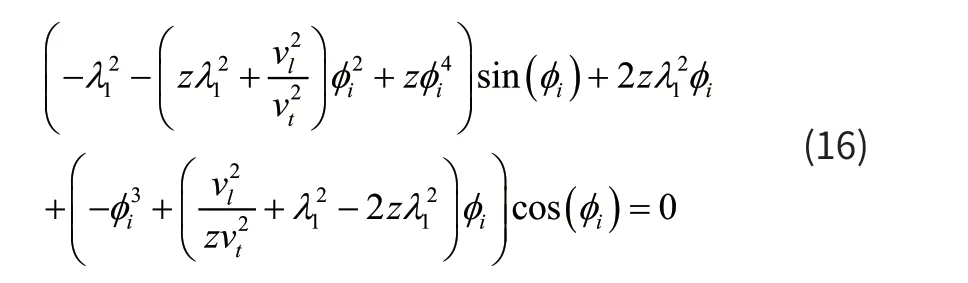
以及频率方程对应的法向振型为:

3 随机风场中系留无人机系统运动响应
3.1 张紧状态下系留无人机系统运动方程离散化
采用伽辽金方法对方程进行截断,由于系缆处于张紧状态,系缆的运动方程主要以前2阶为主,所以对系缆法向运动方程进行了2阶截断。设系缆法向位移为:
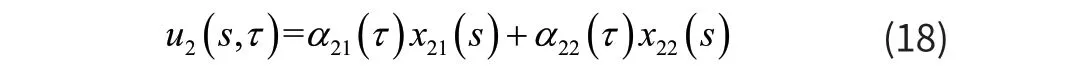
其中x21(s)和x22(s)分别为系缆法向1阶振型和法向2阶振型,通过方程(17)得到。本文将无人机看成质点且与系缆铰接,因此系缆顶端位移与无人机处相等,所以无人机处的法向位移可以表示成:

将方程(18)和(19)代入到系留无人机系统运动方程(8)到(11)中,整理得到:


其中a1~a2,b1~b2,c1~c12,d1~d12以及E1~E6为积分常数。
3.2 随机风速时程模拟
随机风通常由平均风和脉动风组成,其表达式为:

其中Vc为平均风速,Vn(t)为零均值的脉动风速。本文基于Davenport风谱,采用谐波叠加法模拟脉动风,然后加入平均风来模拟随机风。Davenport风谱的表达式为[9]:
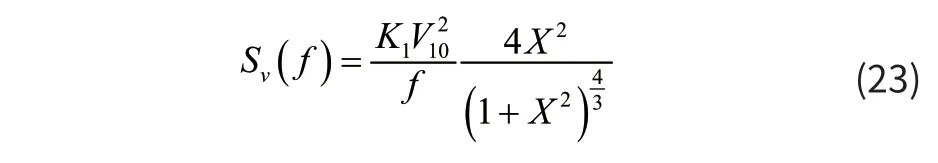
根据Shinozuka理论[10],其随机风速的表达式可以表示成:

Δf为频率增量其表达式为fmin和fmax为频率区段的上限和下限,N为一个充分大的正整数;φj为在 ■■0 ,2π■■上均匀分布的随机变量,fj=fmin+(j- 0.5)Δf。
当平均风速Vc=15m/s、N=2048、V10=7m/s、海面工况K1=0.0025,f为脉动风频率,其取值范围为为湍流积分尺度系数其表达式为时,通过方程(22)到(24)模拟出1000s随机风历程曲线,这里截取200s到1000s的时间历程如图3所示。

图3 Davenport风谱模拟的随机风时程曲线
3.3 随机风场中缆绳位置对系缆法向位移的影响
采用表1中的参数,将方程(22)到(24)代入到系留无人机系统的离散化方程(20)和(21)中,然后采用数值方法进行求解得到系缆不同位置处的法向位移。本文通过概率密度曲线来分析系缆法向位移的大小。从图4可以看出,在S=40m处,系缆法向位移概率密度曲线很陡峭,说明系缆法向位移发生较大位移可能性很小;在S=60m处, S=80m处和S=100m处,系缆法向位移概率密度曲线不断变得平缓,说明系缆法向发生很大位移的可能性开始增加。这是因为系缆顶端与无人机相连,而无人机处所受的风荷载大于系缆所受的风荷载,靠近顶端位置处系缆受无人机运动的影响很大。

表1 系留无人机参数
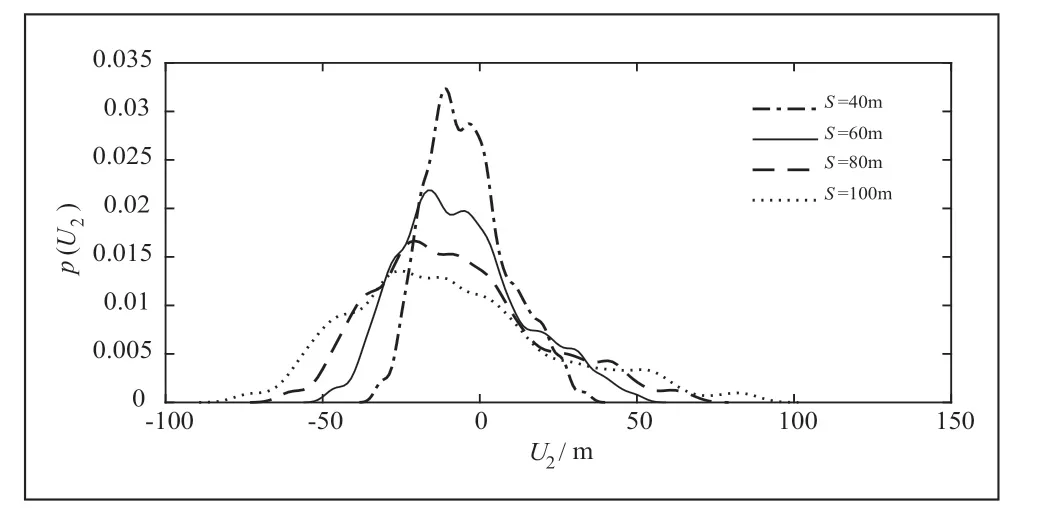
图4 不同位置处系缆法向概率密度曲线
4 结论
本文对张紧状态下随机风场中系留无人机系统运动响应进行了研究。研究发现:在系缆底端,系缆法向位移的概率密度曲线变化很陡峭,说明系缆法向发生较大位移可能性很小;随着系缆位置增加,系缆法向位移概率密度曲线开始变得平缓,说明系缆法向发生较大位移的可能性开始增加。这可能是由于系缆顶端与无人机相连,无人机所受的风荷载相对于系缆较大,所以靠近系缆顶端的系缆受无人机运动的影响,会造成此处系缆的运动剧烈,相应地影响系留无人机系统的正常工作。这些研究为系留无人机系统的设计提供了理论依据。
