HEC-RAS 一、二维模型在水面线计算中的比较分析
2022-02-16粟毅明
粟毅明
(西昌学院 土木与水利工程学院,四川 西昌 615000)
随着河道数值模拟技术的迅速发展, 提高了水面线计算速度与准确性。 如安莉莉[1]利用HEC-RAS与MIKE11对梯形断面河道的计算水位进行了对比分析,认为流量、糙率、坡度分别是单一变量时,小流量下HEC-RAS的计算水位高于MIKE11, 大流量时HEC-RAS的计算水位低于MIKE11。 蒋楠等[2]应用HEC-RAS和MIKE11模型对高安市锦江河段进行水面线计算, 得出MIKE11水面线计算结果略高于HEC-RAS模型,认为模型糙率的敏感性不同是造成水面线结果差异的一个重要因素。 于子铖等[3]以珲春市内河及其北支为例,应用MIKE21与HEC-RAS对现状河道与设计河道水面线进行推求, 并对一维与二维水动力模型的适用性做出建议。 陈雪冬等[4]应用HEC-RAS与MIKE11 两种软件数值仿真成果进行了对比分析,得出HEC-RAS软件计算的水位成果相对MIKE11软件计算的水位成果稍小。 本文以成都市南河百花潭段为例,利用HEC-RAS分别建立了一维与二维河道水动力学模型, 并对水面线的计算结果进行分析。
1 模型介绍
1.1 HEC-RAS一维数学模型
HEC-RAS在恒定流计算基于一维能量方程,如下形式:

式中 Z为水面高程(m);α为动能修正系数;V为断面平均流速(m/s);g为重力加速度(m/s2);hθ为断面间的能量损失(m);下标1,2分别代表下游断面和上游断面。
1.2 HEC-RAS二维数学模型
HEC-RAS二维水动力学模型中控制方程是基于Navier-Stokes方程沿水深平均的平面二维流动基本方程。
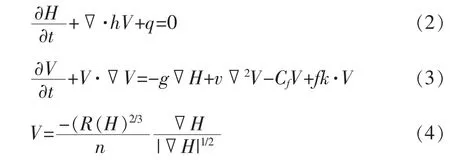
式中 H为水面高程(m);h为水深(m);V为流速(m/s);q为单位河长的汇流量(m2/s);g为重力加速度(m/s2);v为水平方向运动黏度(m2/s);R为水力半径(m);Cf为底摩阻系数;f为柯氏系数;k为垂直单位矢量;n为糙率。
在HEC-RAS中二维模型网格为非结构化网格,采用上述方程组通过半隐式有限体积法计算求解。
2 模型建立
2.1 地形构建
本次采取成都市南河百花潭段实测地形图,全长2.2km,每100~200m测量1个横断面,共布置13个大断面。 利用HEC-RAS每50m差值1个横断面,建立了一维模型XYZ图, 再利用HEC-RAS将一维模型XYZ图生成二维DEM图, 建立的一维模型XYZ图与二维模型DEM图如图1,图2。

图1 一维模型XYZ图

图2 二维模型DEM图
2.2 计算参数及边界条件
在一维与二维河道模型中, 上游边界条件为流量边界, 下游起始水位条件相同, 模型糙率取值0.025。 对于二维模型,本次模型网格步长dx为5m。
3 计算结果
利用HEC-RAS以不同流量300,400,600m3/s对该河段计算出水面线。 二维模型取值横断面网格的平均水位高程。 计算结果如表1,图3为二维模型计算成果。
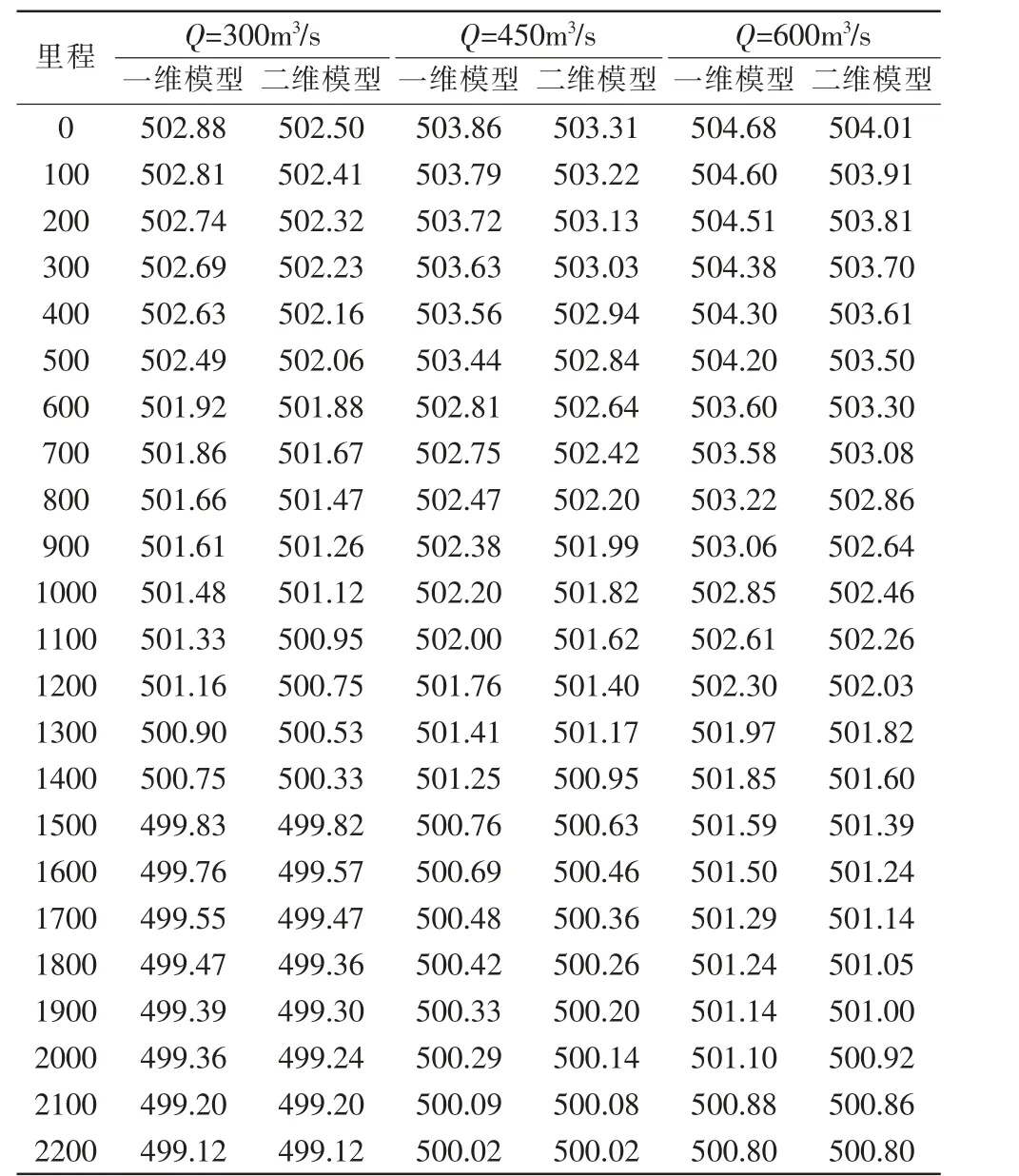
表1 不同流量下的水面线计算成果
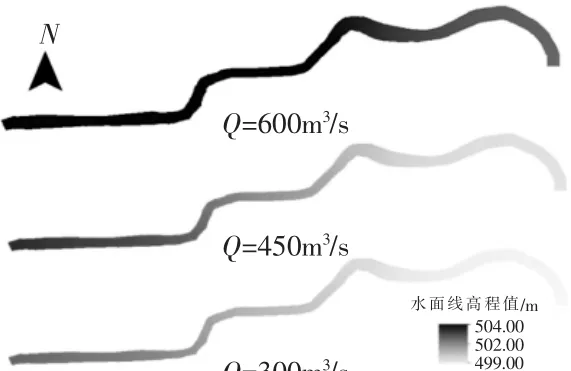
图3 不同流量下的二维模型水面线
4 结果分析
4.1 计算成果分析
由图4可知,一维模型普遍比二维模型计算的水位高, 一维与二维模型的计算水位成果与里程变化趋势大体相同。 对于Q=300m3/s工况下,一维与二维模型的差值在0~0.47m之间,Q=450m3/s工况下,一维与二维模型的差值在0~0.62m之间。 对于Q=600m3/s工况下,一维与二维模型的差值在0~0.70m之间。 模型差异较大处出现在模型上游边界范围附近。 随着远离模型的上游边界,两者差值呈减小趋势。
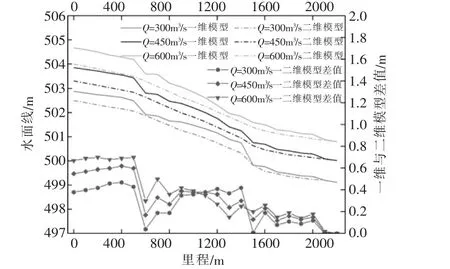
图4 模型计算成果
4.2 糙率因素分析
糙率是影响结果的重要参数, 本次对水面线结果进行糙率单因素分析,其他因素保持不变。本次以Q=300m3/s为例,对一维模型与二维模型河道糙率值进行探讨,设定不同糙率值0.025,0.030,0.035,其他参数不变,计算结果如表2。
根据表2,表3可知,糙率单一变量时,一维模型比二维模型计算的水位高,差值比率为0~0.09%。

表3 不同糙率下水面线差值对比
本次以Q=300m3/s,糙率n=0.030为例,对一维模型与二维模型河道糙率值进行探讨,设定±17%、±10%、0为变化幅度,其他参数不变。 根据各断面变幅下的水位取平均值。 水面线对糙率的敏感性分析如表4。
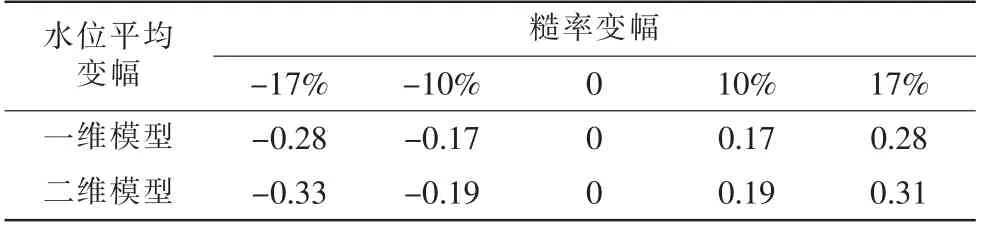
表4 水面线对糙率的敏感性分析
由表4可知,当糙率变幅在±10%时,两者的绝对水位平均变幅差为0.02m,当糙率变幅在±17%时,两者的绝对水位平均变幅差0.03m与0.05m。 河道糙率变幅相同条件下时,一二维模型的敏感性差距不大。
4.3 二维模型在不同网格步长下的分析
本次对二维模型进行不同大小的网格剖分,以Q=300m3/s为例,设定不同的空间步长dx值,分别是2.5,5,10,15m,一二维模型边界条件保持相同,其他参数不变,计算结果如表5。

表5 二维模型在不同dx下的水面线成果
由表5可知一维模型的计算水位普遍高于二维模型, 对于不同空间步长的二维模型计算水位差值在0~0.08m之间,变化较小。 分析原因是本次计算的河道断面较为规整,水下地形起伏较小。
5 结语
(1)在相同的断面数据、边界条件及糙率下,一维模型与二维模型的计算水位成果与沿程变化趋势大体相同,一维模型普遍比二维模型计算的水位高。由于模型边界条件的影响, 在模型边界较附近的水面线计算差异较大, 建议模型计算时适当延长模型上游范围,以降低模型边界对计算结果的影响。
(2)糙率单一变量时,一维模型比二维模型计算的水位高,差值比率在0%~0.09%之间。 河道糙率变幅相同的条件下时,一、二维模型的敏感性差距不大。
(3)二维模型计算断面较为规整,水下地形起伏较小的河道时, 采用不同空间步长计算的水面线差值较小, 因此对于此类河道, 可采用较大的空间步长,减少计算运行时间。
