泡沫金属流道对PEMFC性能的影响
2022-02-16孙峰苏丹丹殷宇捷庞彬董小平李志远
孙峰,苏丹丹, ,殷宇捷,庞彬, ,董小平,,李志远,
(1.河北大学 质量技术监督学院,河北 保定,071000;2.河北省新能源汽车动力系统轻量化技术创新中心,河北 保定,071000)
质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)是一种利用可再生能源氢能的电化学能量转换装置,具有转换效率高、响应速度快、可靠性好、无污染等优点[1-3]。双极板是组成PEMFC的核心部件之一,双极板两侧的流道结构是反应气体流动的通路。合理的流道结构设计对改善反应气体传输效果和促进电化学反应非常关键[4-5]。
目前,国内外学者对传统流道的结构优化进行了大量研究[6]。MOHAMMEDI等[7]研究了30 种流道截面形状对PEMFC性能的影响,发现流道截面形状对PEMFC功率密度有显著影响,当流道截面形状是底部为梯形、顶部为倒梯形时,PEMFC输出性能最佳。KERKOUB等[8]研究了插指形流道、蛇形流道以及直流道的肋宽比(流道与肋板的宽度之比)对PEMFC性能的影响,当工作电压较低时,增大肋板宽度和减小流道宽度可加强肋板下方的反应气体对流效应,提高电流密度分布的均匀性。CAI等[9]设计了一种新型波浪挡板,当波浪的幅值为0.305 mm、循环次数为3.52 时,PEMFC输出功率密度比常规直流道提高了2.2%。TROGADAS等[10]设计了一种肺形仿生流场,发现肺形流场能够强化传热传质,提高反应气体的利用率。SHEN等[11]结合场协同原理对3D 流道进行研究,发现3D流道可以有效去除液态水,且提高入口速度有利于增强液态水的去除效果。
具有高孔隙率和高电导率的泡沫金属材料,可作为PEMFC 的一种新型流场结构[12]。CARTON等[13]建立了泡沫金属PEMFC模型,并与平行流场进行了对比,结果发现,在金属泡沫流场中,反应气体从入口到出口的浓度分布均匀性更佳。AFSHARI等[14]发现泡沫金属流场能够强化反应气体传递、改善电流密度与温度分布。HUO等[15]对具有泡沫镍阴极流场的PEMFC 进行了实验测试,在相同工作条件下,与平行流道相比,具有金属镍流场的PEMFC 的最大净功率密度更高。AZARAFZA等[16]发现,与平行流场相比,泡沫金属流场峰值功率密度提高了约50%;与蛇形流场和交错流场相比,泡沫金属流场峰值功率密度提高了约10%。LIU等[17]通过优化PEMFC操作参数,提高了泡沫镍流场的输出性能,优化后的操作参数如下:电池温度为80 ℃,加湿温度为75 ℃,化学计量比为2。BAO等[18]发现增加泡沫金属表面的疏水性或减小泡沫孔径有助于去除流场中的液滴。KANG等[19]设计了具有不同孔隙率梯度的泡沫金属流场,与常规泡沫金属流场相比,具有孔隙率梯度泡沫金属流场的PEMFC最大功率密度提高了8.23%。
由上可知,采用泡沫金属作为气体流场可强化PEMFC的传质特性并改善其输出性能。本文作者采用泡沫金属代替PEMFC的阴阳极流道,通过与传统直流道进行对比,研究泡沫金属对PEMFC反应气体压力降、摩尔分数分布以及电流密度的影响。在此基础上,详细分析孔隙率对泡沫金属流道反应气体传输以及PEMFC 输出性能的影响,并对泡沫金属流道进行孔隙率优化,为双极板流道结构优化提供理论指导和技术支持。
1 PEMFC模型建立
1.1 泡沫金属形貌
通过选用不同的金属基质以及制作工艺,可以制备出具有不同性能的泡沫金属材料。常见泡沫金属的微观形貌如图1所示。目前,常用的泡沫金属模型有十四面体模型、十二面体模型、八面体模型、立方孔模型、Gibson-Ashby 模型以及CT重构模型[20]。

图1 泡沫金属的微观形貌Fig.1 Micromorphologies of foam metals
本文采用立方孔模型进行仿真测试,以正六面体为基体,在六面体各顶点、线中心以及面中心各放置球体,运用布尔运算构成如图2所示的泡沫金属单元结构,通过改变球体直径获得不同孔隙率的泡沫金属。
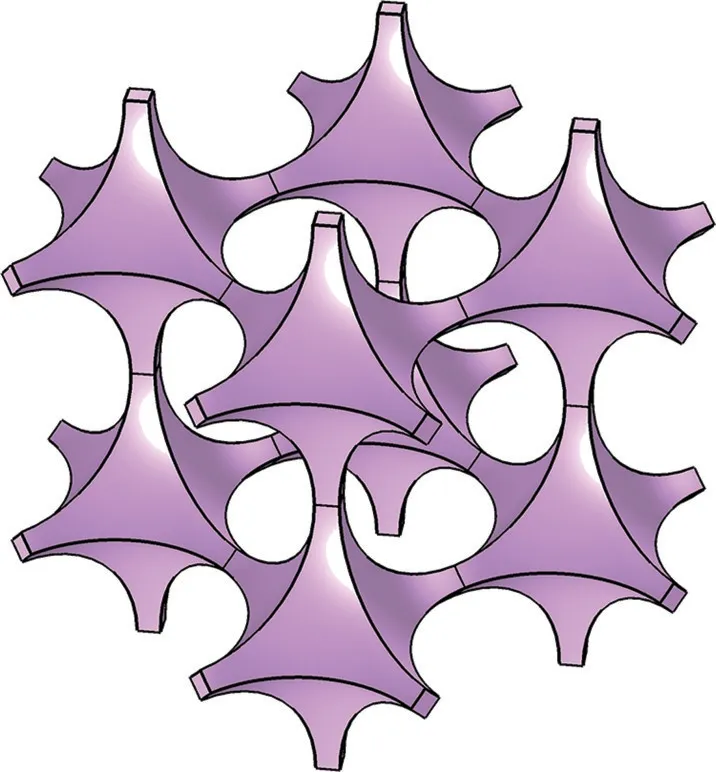
图2 泡沫金属立方孔模型单元结构Fig.2 Cell structure of foam metal cubic hole model
1.2 计算模型
本文建立的PEMFC 几何模型包含阴阳极的泡沫金属流道、扩散层、催化层及质子交换膜等。在直流道模型中,氢气和氧气分别进入阳极和阴极流道内,通过扩散层到达催化层发生电化学反应。在PEMFC泡沫金属流场中,氢气和氧气通过流场中的金属空隙流动,由于泡沫金属具有较高的孔隙率,反应气体可更充分地进入扩散层中。PEMFC几何模型如图3所示,模型参数见表1。
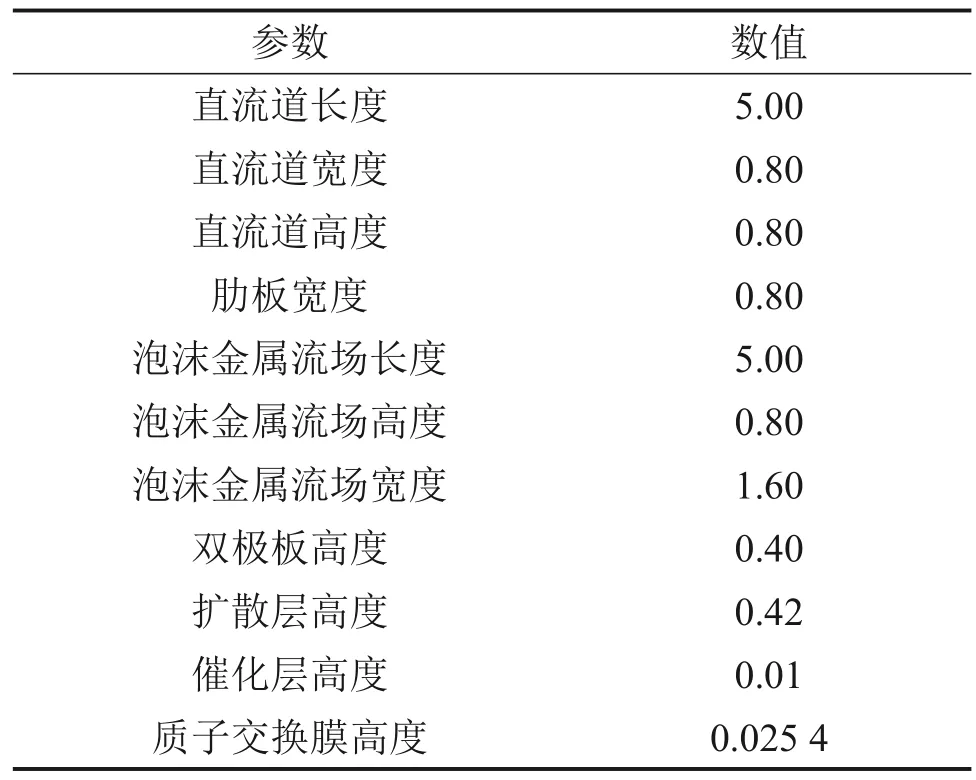
表1 PEMFC几何模型参数Table 1 Parameters of PEMFC geometric model mm
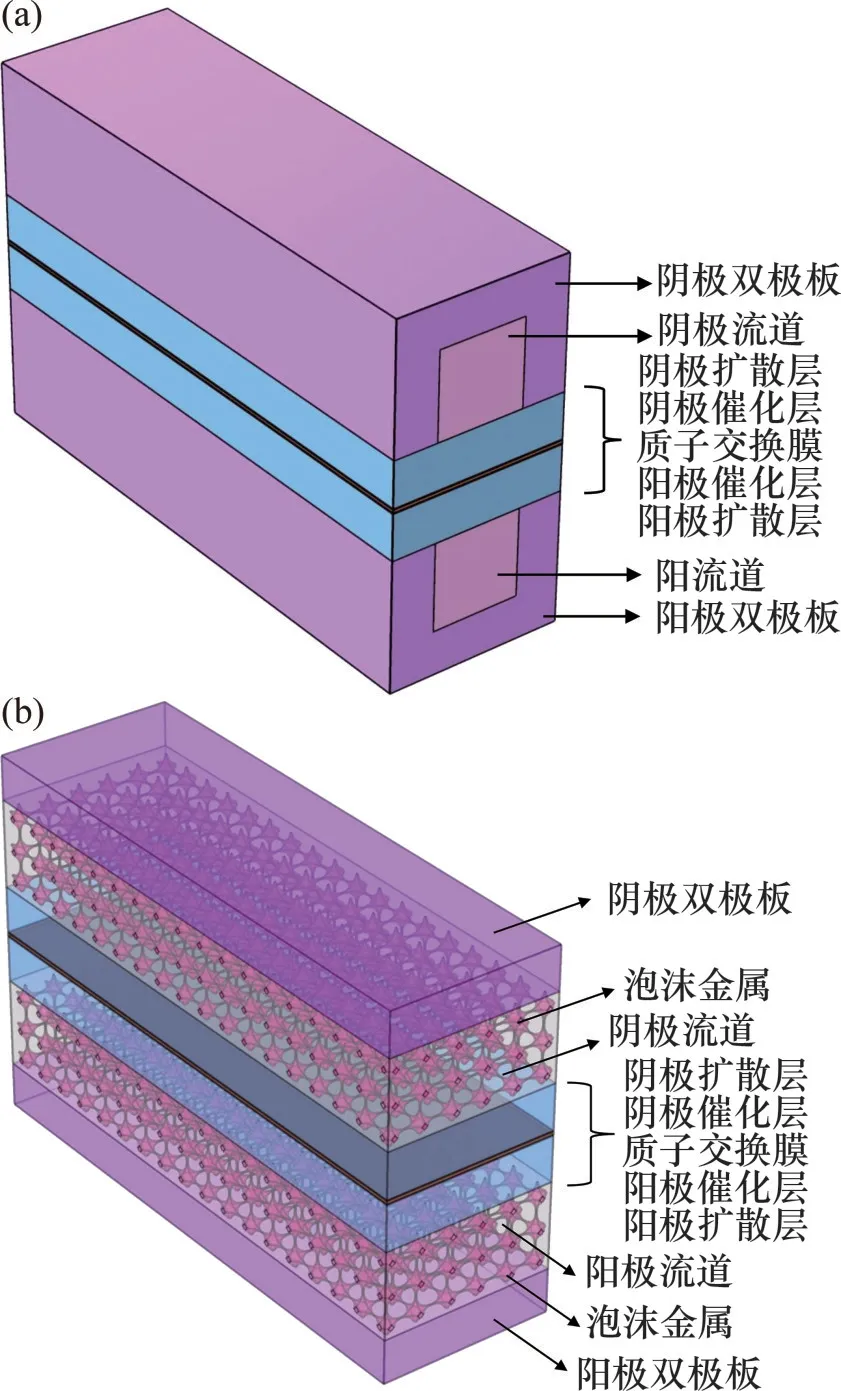
图3 PEMFC几何模型Fig.3 Geometry model of PEMFC
1.3 模型假设
本文的模型假设为:1) PEMFC 处于稳定工作状态;2) 模型内水的存在形式为气态;3) 反应气体为理想气体;4) 反应气体流动为层流;5) 扩散层等多孔介质材料均为各向同性;6) 忽略重力影响。
1.4 控制方程
质量守恒方程:
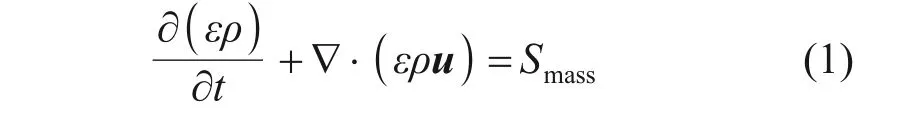
式中:ε为多孔介质孔隙率;ρ为反应气体混合物密度,kg/m3;u为反应气体混合物速度矢量,m/s;Smass为质量源项,kg/(m·s)。
动量守恒方程:
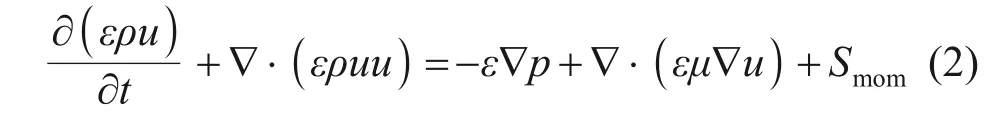
式中:p为反应气体压力,Pa;μ为反应气体动力黏性系数,N·s/m3;Smom为动量源项,N/m3。
能量守恒方程:
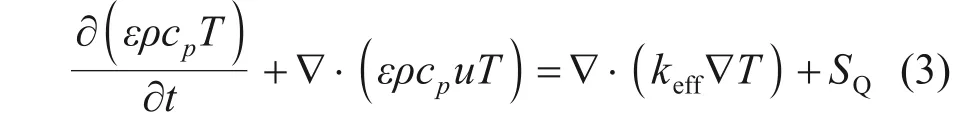
式中:cp为比定压热容,J/(kg·K);keff为有效热导率,W/(m·K);SQ为能量源项,W/m3。
组分传输方程:
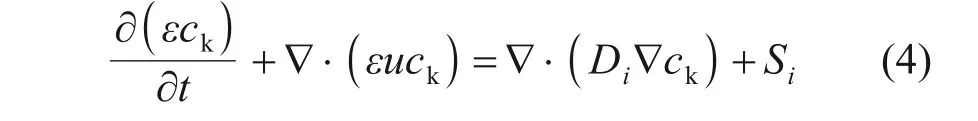
式中:ck为组分质量浓度,kg/m3;Di为组分有效扩散系数,m2/s;Si为组分源项,kg/(m·s)。
电荷守恒方程:
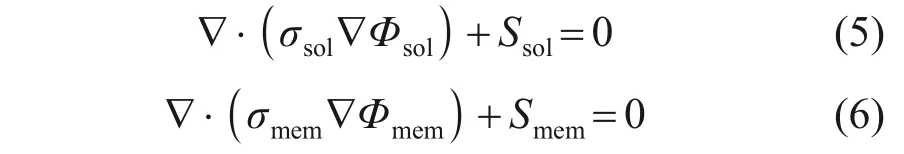
式中:σsol和σmem分别为固相和膜相电导率,1/(Ω·m);Φsol和Φmem分别为固相和膜相电势,V;Ssol和Smem分別为固相电势与膜相电势的源项,A/m3。
电化学方程:
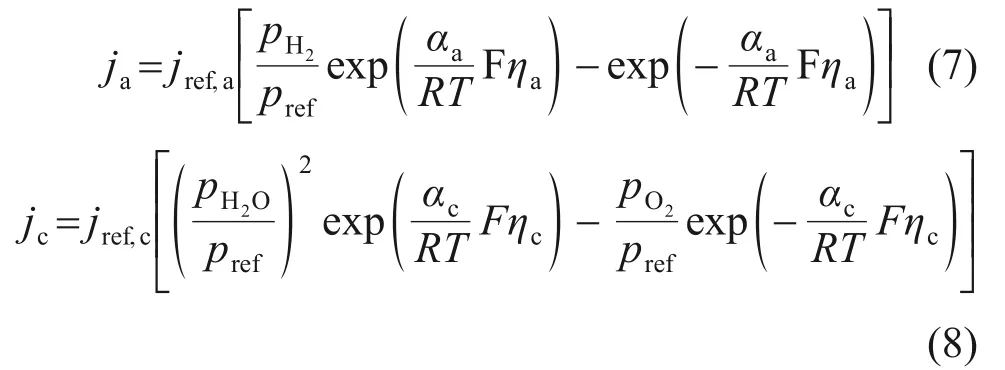
式中:jref,a为阳极参考交换电流密度,A/cm2;jref,c为阴极参考交换电流密度,A/cm2;pH2,pO2和pH2O分别为氢气、氧气和水蒸气的分压,Pa;pref为参考压力,Pa;αa和αc分别为阳极和阴极传递系数;ηa和ηc分别为阳极和阴极活化过电压,V;R为摩尔气体常数,8.314 J/(mol·K);T为反应温度,K;F为法拉第常数,C/mol。
1.5 边界条件
PEMFC 流场入口设置为速度入口,流场出口设置为压力出口。PEMFC阴阳极的反应气体通道、扩散层以及催化层外侧边界应用对称边界条件,其他边界应用无滑移边界条件。阳极双极板边界设为零电位,阴极双极板边界设为PEMFC 电势,其他外部边界均绝缘。仿真过程中的操作参数如表2所示。
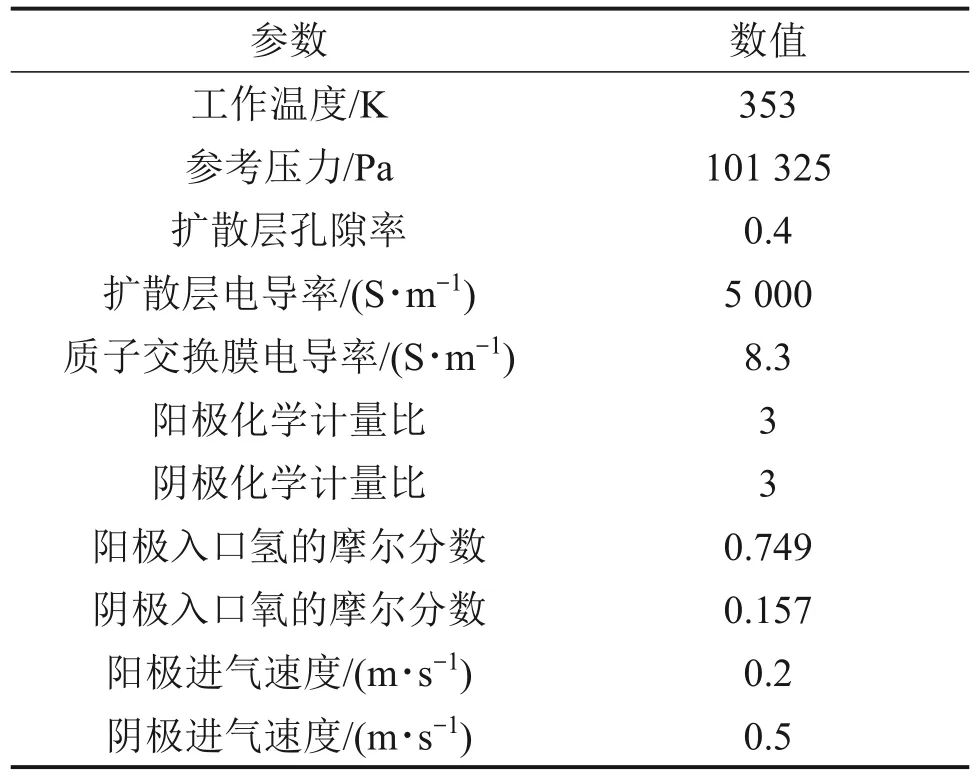
表2 PEMFC操作参数Table 2 Operating parameters of PEMFC
1.6 网格无关性验证
分别选取580 943,725 047和897 184个网格,对孔隙率为0.90的泡沫金属模型极化特性进行模拟仿真。当输出电压为0.48 V时,3种网格数量模型的电流密度分别为1.552 3,1.566 4 和1.569 9 A/m2。结果表明,725 047个网格与580 943个网格的电流密度绝对误差为0.014 1 A/m2,与897 184个网格的电流密度绝对误差为0.003 5 A/m2,误差满足仿真计算要求,为减小计算量并保证计算的准确度,选取725 047个网格的划分方法进行模拟计算。
1.7 模型验证
本文建立与文献[21]中相同的直流道模型,并采用相同的操作参数(表2)。图4所示为PEMFC极化曲线对比。由图4可知:在低电流密度区,仿真曲线与文献[21]中曲线的变化规律均一致;在高电流密度区,由于实验中在流道内生成了液态水,降低了由流道向催化层传递的反应气体浓度,造成电压损失,故在相同电流密度下PEMFC的仿真结果高于实验结果。总体而言,验证了本文所建几何模型的有效性。
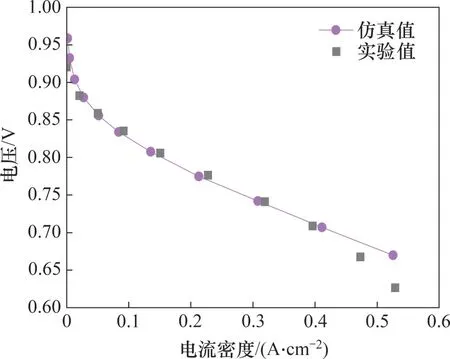
图4 PEMFC极化曲线对比Fig.4 Comparison of polarization curves
2 结果与分析
本文主要对泡沫金属阴极流道内的反应气体进行分析。首先将直流道与孔隙率为0.90 的泡沫金属流道进行对比,然后分析泡沫金属流道孔隙率分别为0.90,0.85,0.80 和0.75 时的反应气体分布以及极化曲线和功率密度曲线,最后对泡沫金属流道孔隙率进行优化。
2.1 泡沫金属流道与直流道对比
2.1.1 氧气压力分布
图5 所示为工作电压为0.48 V 时2 种流道模型的氧气压力对比。由图5可知:泡沫金属流道内气体压力分布更加均匀,有利于反应气体在流道内的扩散。此外,由于电化学反应的进行,2种模型中的氧气不断被消耗,氧气压力从入口到出口逐渐降低,呈阶梯状分布。
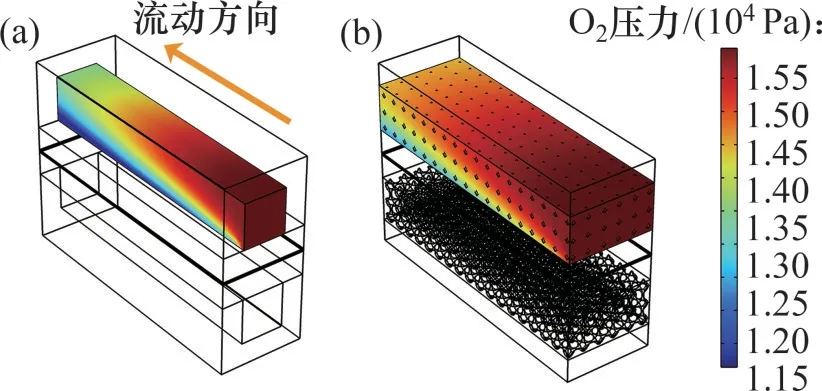
图5 不同几何模型的氧气压力对比Fig.5 Comparison of oxygen pressure with different geometric models
由图5 还可知:2 种流道模型在流道入口与出口的氧气压降差别较大。直流道模型与泡沫金属流道模型的氧气平均压降Δp分别为3.427×103Pa和2.101×103Pa,泡沫金属流道模型的压降比直流道模型压降降低了38.7%,这是由于与传统直流道模型的肋板结构相比,泡沫金属流道模型大大减小了反应气体的流动阻力,降低了反应气体的压降。泡沫金属流道模型气体压降较低,有利于反应气体的充分扩散。
2.1.2 氧气摩尔分数分布
图6 所示为工作电压为0.48 V 时2 种流道模型的氧气摩尔分数分布对比。由图6 可知:2 种流道模型在沿反应气体流动方向的氧气摩尔分数均因电化学反应的进行而降低。直流道模型与泡沫金属流道模型在扩散层中的氧气平均摩尔分数分别为0.059 9 和0.094 0,泡沫金属流道模型扩散层中的氧气平均摩尔分数比直流道模型提高了56.9%,且分布更加均匀。这是由于泡沫金属流道模型的泡沫结构增加了流道内反应气体与扩散层的接触面积,强化了氧气向扩散层中的传输效果。

图6 不同几何模型的氧气摩尔分数对比Fig.6 Comparison of oxygen mole fraction with different geometric models
2.1.3 极化曲线与功率密度曲线对比
图7所示为直流道模型和泡沫金属流道模型的极化曲线与功率密度曲线对比。由图7可知:直流道模型与泡沫金属流道模型PEMFC的峰值功率密度分别为0.726 W/cm2和0.900 W/cm2,泡沫金属流道模型的峰值功率密度比直流道模型提高了23.9%。泡沫金属流道能够提高PEMFC 峰值功率密度的原因主要包括2个方面:一是由于泡沫金属流道较小的压力损失,有利于促使电化学反应稳定进行,提升输出性能;二是由于泡沫金属流道的反应气体摩尔分数分布均匀性更佳,强化了反应气体由流道向扩散层的质量传递,减小了由传质极化造成的电压损失。
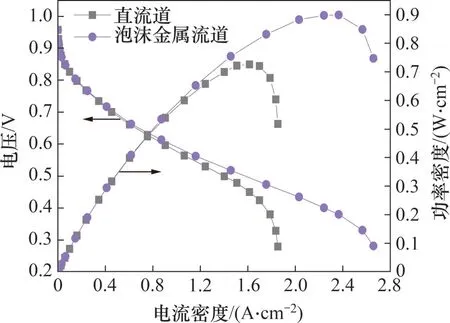
图7 不同几何模型的极化曲线与功率密度曲线Fig.7 Polarization curves and power density curves with different geometric models
2.2 不同孔隙率的泡沫金属流场对比
2.2.1 孔隙率对氧气压力的影响
图8 所示为工作电压为0.48 V 时不同孔隙率(孔隙率分别为0.90,0.85,0.80 和0.75)泡沫金属流道的氧气压力对比。由图8可知:靠近泡沫金属流道出口处的氧气压力随孔隙率减小而明显降低。为定量分析孔隙率对氧气压力分布的影响,计算流道入口与出口的氧气压降。当泡沫金属流道的孔隙率为0.90,0.85,0.80 和0.75 时,流道氧气压降分别为2.101×103,2.330×103,2.372×103和2.530×103Pa,由此可知,流道压降随孔隙率降低而增大。这是由于孔隙率的降低导致泡沫金属骨架的体积分数增大,增加了反应气体的流动阻力,氧气在流道内的压力损失增加。
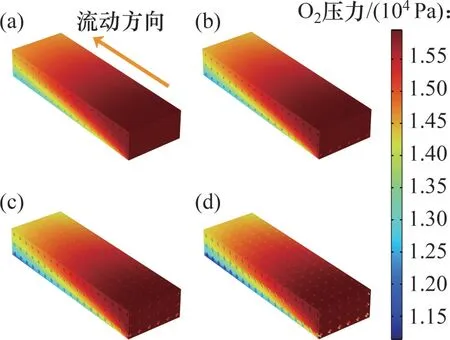
图8 不同孔隙率的模型氧气压力对比Fig.8 Comparison of oxygen pressure of different porosity models
2.2.2 孔隙率对氧气摩尔分数的影响
图9所示为工作电压为0.48 V时不同孔隙率泡沫金属流道的氧气摩尔分数对比。为分析孔隙率对氧气分布的影响,提出衡量氧气摩尔分数均匀性的指标λ(式(9)),氧气摩尔分数分布越均匀,均匀指标λ越大,反之,均匀指标越小。表3所示为不同孔隙率泡沫金属流道的氧气摩尔分数均匀性指标的计算结果,λ1与λ2分别为在流道内与扩散层中的氧气摩尔分数均匀性指标。
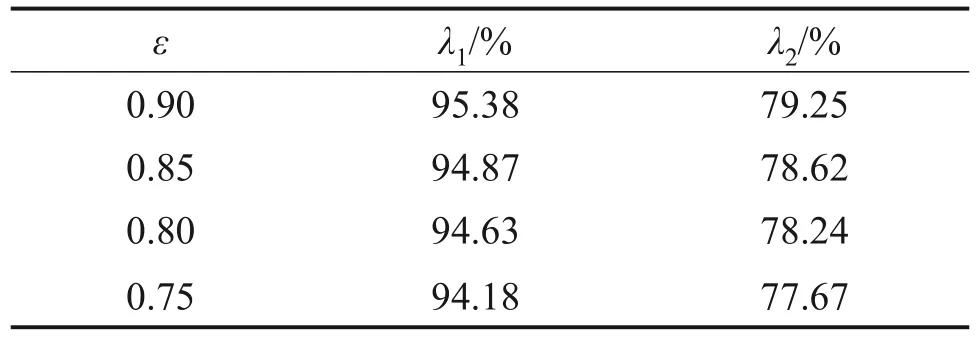
表3 氧气摩尔分数均匀性指标Table 3 Oxygen mole fraction uniformity index
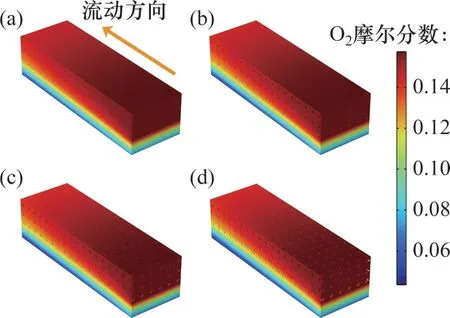
图9 不同孔隙率模型的氧气摩尔分数对比Fig.9 Comparison of oxygen mole fraction with different porosity models
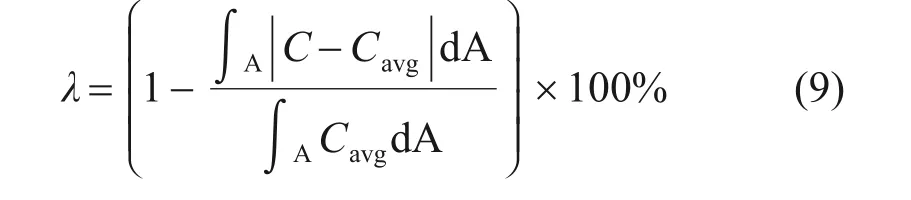
式中:C为局部氧气摩尔分数,Cavg为平均氧气摩尔分数。
由表3可知:随着孔隙率的降低流道内和扩散层中的氧气摩尔分数均匀性指标也减小。由此可知,随着孔隙率降低,泡沫金属流道内的氧气分布均匀性下降,氧气由流道向扩散层中的传递效果减弱,导致扩散层中的氧气摩尔分数降低。
2.2.3 孔隙率对极化曲线与功率密度曲线的影响
图10 所示为不同孔隙率泡沫金属流道的极化曲线与功率密度曲线对比。由图10 可知:当孔隙率为0.75,0.80,0.85 和0.90 时,泡沫金属流道的峰值功率密度分别为0.858,0.877,0.888 和 0.900 W/cm2;当孔隙率ε=0.90 时,PEMFC 的峰值功率密度最高,输出性能最好。这是由于增大孔隙率,可以减小泡沫金属骨架的体积分数,降低泡沫金属骨架对反应气体流动的阻力,从而减小反应气体压降,有助于强化反应气体向扩散层的传输,提高PEMFC输出功率。
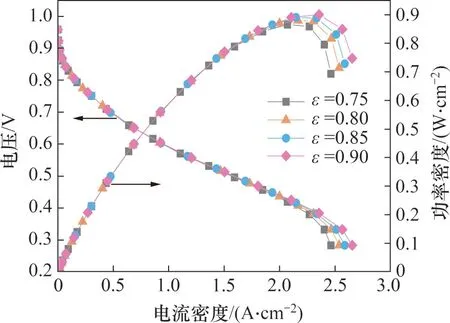
图10 不同孔隙率模型的极化曲线与功率密度曲线Fig.10 Polarization curves and power density curves with different porosity models
2.3 泡沫金属流道孔隙率优化
为深入研究泡沫金属流道孔隙率对PEMFC 输出性能的影响,建立泡沫金属流道的分层模型,并对孔隙率梯度进行优化。孔隙率分层模型分别沿气体流动方向和厚度方向将泡沫金属阴极流道等分为n个子层,各子层均为各向同性,当n=3时,泡沫金属阴极流道沿气体流动方向和厚度方向的分层模型如图11 所示。分层模型中的第1 个子层为n1,其孔隙率为ε1,第i个子层为ni,其孔隙率为εi,第i+1个子层的孔隙率为εi+1。各子层间的孔隙率梯度k为
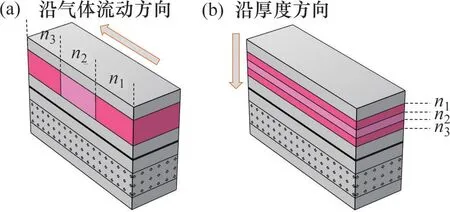
图11 泡沫金属阴极流道分层模型Fig.11 Layered model of foam metal cathode flow channel
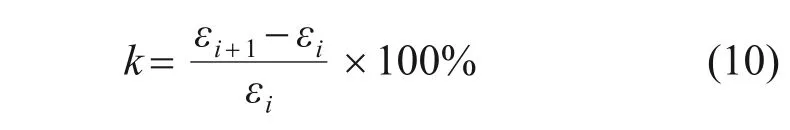
2.3.1 泡沫金属流道孔隙率分层方案
泡沫金属流道孔隙率分层方案如表4所示,其中Case1 沿气体流动方向进行分层,Case2 沿厚度方向进行分层。
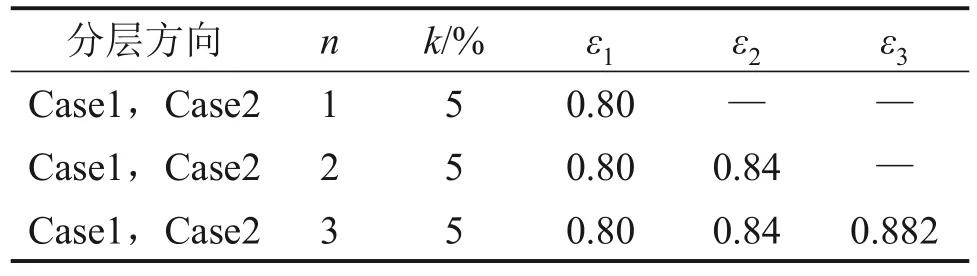
表4 泡沫金属流道分层方案Table 4 Layering method of foam metal flow channel
图12(a)所示为孔隙率分层方案采用沿气体流动方向时泡沫金属流道PEMFC的极化曲线与功率密度曲线。当子层数n为1,2 和3 时,PEMFC 的峰值功率密度分别为0.879,0.881 和0.885 W/cm2。由此可见,增加沿气体流动方向的子层数量能够提高PEMFC的峰值功率密度。当n=3时,PEMFC峰值功率密度比n=1时提高0.68%。这是由于沿气体流动方向对泡沫金属流道进行分层时,可使出口附近的孔隙率增大,减小氧气流动阻力,改善出口附近的氧气分布。
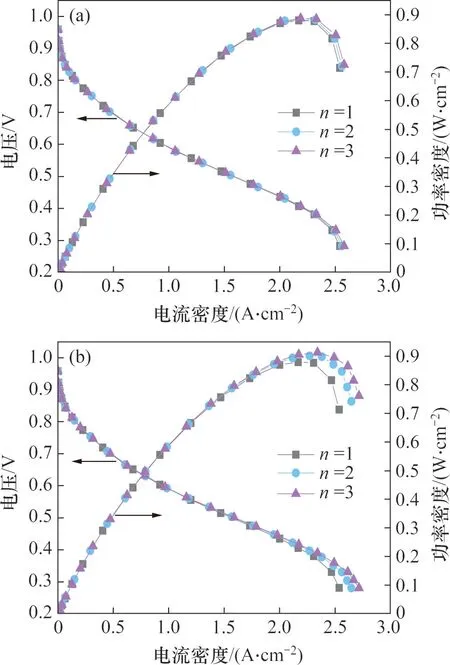
图12 不同层数的极化曲线与功率密度曲线Fig.12 Polarization curves and power density curves of models with different layers
图12(b)所示为孔隙率分层方案采用沿厚度方向时泡沫金属流道PEMFC的极化曲线与功率密度曲线。当子层数为1,2 和3 时,PEMFC 的峰值功率密度分别为0.879,0.901 和0.913 W/cm2。由此可见,增加沿厚度方向的子层数量能够提高PEMFC的峰值功率密度。当n=3时,PEMFC峰值功率密度比n=1时提高3.87%。这是由于沿厚度方向对泡沫金属流道进行分层时,靠近扩散层的子层孔隙率提高,氧气扩散阻力减小且氧气与扩散层的接触面积增大,对氧气由流道向扩散层的传质强化效果更佳。
2.3.2 泡沫金属流道孔隙率梯度
泡沫金属流道模型孔隙率梯度方案如表5 所示,其中Case1 沿气体流动方向进行分层,Case2沿厚度方向进行分层。
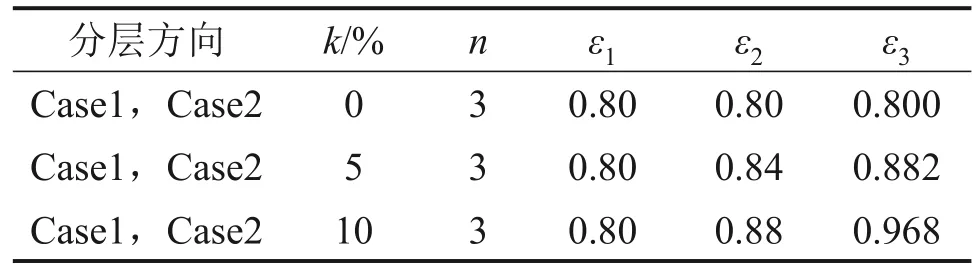
表5 泡沫金属流道孔隙率梯度方案Table 5 Porosity gradient scheme for foam metal flow channel
图13 所示为不同孔隙率梯度泡沫金属流道PEMFC 的极化曲线与功率密度曲线。由图13 可知:当孔隙率梯度k为0,5%和10%时,在沿气体流动方向的分层模型中,PEMFC 的峰值功率密度分别为0.879,0.885 和0.885 W/cm2;在沿厚度方向的分层模型中,PEMFC 的峰值功率密度分别为0.879,0.913 和0.900 W/cm2。通过对比可知,在沿厚度方向采用孔隙率梯度时,泡沫金属流道PEMFC 的输出性能明显提升。当沿厚度方向孔隙率梯度k=5%时,PEMFC 的峰值功率密度最大,比k=0 时提高了3.87%。这是由于增大沿厚度方向的孔隙率梯度,可减小泡沫金属骨架的体积分数,反应气体流动阻力降低,优化了反应气体的质量传递效果,有利于降低传质电压损失。
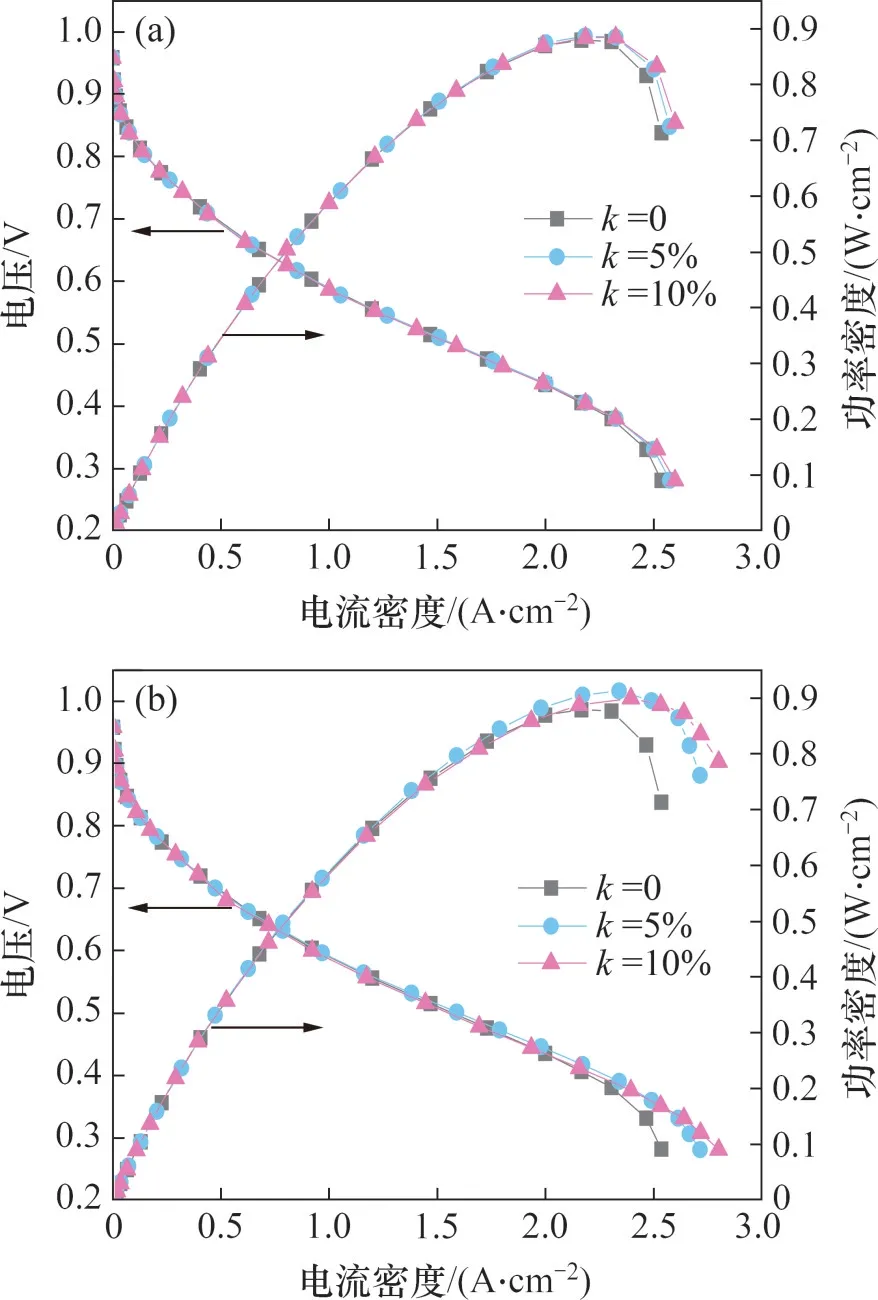
图13 不同孔隙率梯度的极化曲线与功率密度曲线Fig.13 Polarization curves and power density curves of models with different porosity gradients
3 结论
1) 与直流道相比,泡沫金属流道内氧气压降减小了38.7%,扩散层中的氧气平均摩尔分数提高了56.9%,PEMFC峰值功率密度提高了23.9%。
2) 增大泡沫金属流道的孔隙率,可减小氧气的流动阻力,使流道入口与出口间的氧气压降减小,改善流道内氧气分布的均匀性,提高PEMFC的输出性能;当孔隙率ε=0.90 时,PEMFC 的峰值功率密度为0.900 W/cm2。
3) 增大沿气体流动方向和厚度方向的分层数量均能够提高PEMFC的峰值功率密度。采用沿气体流动方向的分层方案,分层数n=3 时的PEMFC峰值功率密度比n=1时提高0.68%;采用沿厚度方向的分层方案,分层数n=3 时的PEMFC 峰值功率密度比n=1时提高3.87%。
4) 沿厚度方向采用孔隙率梯度设计能够明显提高泡沫金属流道PEMFC 的输出性能。当孔隙 率梯度k=5% 时,PEMFC 的峰值功率密度为 0.913 W/cm2,比k=0时提高了3.87%;继续增大k,PEMFC的峰值功率密度反而减小。
