聚类和关联算法在学生学业分析中的应用

苏 锦，罗锦光

(广西电力职业技术学院，广西 南宁 530007)

0 引言

自我国高职院校开始信息化建设以来，各院校的信息系统中存放着每届学生的各类数据。由于高职生活相比起高中、中职的生活要相对自由，学生在来到高职院校后对学习方法、自我管理有可能会做不到位，导致了每学期均会出现部分学生考试不及格的现象发生，影响了学生的正常发展。通常当学生在课程学习中投入的学习时间不足、方法不对，往往成绩较差，当学生在课程学习之中积极努力，课程成绩通常较好，付出的努力往往与学业成绩成正比，即俗语中的“一分耕耘一分收获”。此外，课程与课程间也存在相互关系，如果在关联性较强的课程学习中，一门课程学不好，可能导致与该门课程有联系的相关课程都学不好的结果。本文利用数据挖掘对学生学习过程中的相关数据加以分析，验证“一分耕耘一分收获”的科学依据，找出课程间的关联，为提升高职院校的教学方法、改善学生的学习方式和降低学业预警提供了一定的参考。

1 算法原理

1.1 改进型KMeans算法

聚类挖掘可以在大量的数据中，把具有相似特征的数据进行子集划分，不同子集之间拥有尽可能远的距离，即同一子集数据相似，不同子集数据相异的原则，将数据集分割为若干子集，方便观察者了解数据分布情况。聚类的过程不需要对数据进行标记，由算法自动完成数据聚类过程，因此聚类也称无监督归纳。常用的聚类算法有利用数据分布密度聚类、利用数据分层聚类、基于划分聚类等。聚类挖掘在生物工程领域，根据基因功能获取生物种群的结构特征，在市场分析领域，常用在识别不同客户群体的消费特征，在互联网领域，能够对Web信息进行分类管理，提升客户搜索效率。

KMeans算法作为聚类算法中最经典的算法，属于基于划分的聚类挖掘方法。KMeans算法利用随机的k个焦点作初始数据集子类的中心点，依据其他各点到各子集中心点的欧几里得距离，将其他各点各自分配到最近的中心点所在子集，然后对形成的子集内部的点重新计算出距离平均值求出新的中心点，进而再次计算其他各点到新的各中心点距离，再次将各点归纳到距离最小的新中心点形成子集，如此迭代，直到形成的各子集不再发生变化则终止[1]。KMeans算法作为一种数据预处理方法使用时，通常k的数值不会选择太大，具有算法复杂度低、伸缩性较好、容易理解等优点。但是传统的KMeans算法当随机中心变化时，对于最终子集的形成也有较大差别，因为聚心以距离均值方式计算，易受离群极值点的影响，极有可能导致局部最优解等缺点，因此需要进行改进。

改进型KMeans算法主要针对传统KMeans算法的初始中心点选择进行改进。其核心思想是初始子集中心间距离尽可能地相距较远[2]。先随机选择数据集中一个点作为中心点c1，计算数据集中其他点到已知中心点的距离D(x)大小，选取D(x)最大的点作为第ci个聚类子集中心点，重复计算数据集中其他点到已知中心点的距离D(x)大小，并选取D(x)最大的点作为第Ci+1个聚类子集中心点，直到选出k个聚类子集中心点，之后就使用标准KMeans算法，划分子集。

1.2 Apriori算法

关联挖掘可以在数据集中找出数据单元与单元之间的相互关系，挖掘出由单元A发生的情况下推导出单元B发生的概率或是影响，进而用以描述数据单元同时发生的规律[3]。关联规则常用于电商广告，用以推送用户感兴趣的商品，也常用于气象因素分析等领域。

Apriori算法可以用来挖掘强关联规则，是最常见的关联算法之一。算法的核心是通过设置最小支持度和最小置信度，扫描数据库，产生频繁项集和生成规则，假定有一条规则的支持度和置信度大于等于预设的最小支持度和最小置信度，则认为该规则是强关联规则[4]。假设有一个由A、B、C、…若干事务组成的数据集合D，其中支持度是可以表示为A事务在数据集D中出现的计数记为,SupportA=P(A)，A事务和B事务的支持度则是A事务和B事务同时出现在数据集D中的计数,记为Support(A&B)=P(A&B)，支持度主要体现事务的有效性；置信度是同时包含有A事务和B事务的计数占全部A事务计数的比例，记为Confidence(A&B)=P(A&B)/P(A)，置信度主要体现事务的确定性；提升度是“同时包含A事务和B事务计数与A事务计数的比例”和“B事务计数”的比值，记为Lift(A&B)=P(A&B)/P(A)/P(B)，提升度体现A事务和B事务的相关性，提升度大于1表明A事务与B事务正相关，提升度小于1表明A事务与B事务负相关，提升度等于1表明A事务与B事务无关。

Apriori算法主要由以下几个步骤组成：

步骤1：预设最小支持度和最小置信度；

步骤2：扫描数据库累进计算数据项出现的计数，获取大于等于最小支持度计数的项，形成频繁1项集；

步骤3：在频繁1项集基础上，继续累进计数，获取大于等于最小支持度计数的频繁2项集，如此执行，直到不能继续形成频繁k项集；

步骤4：依据最小置信度生成强关联规则。

2 学生学业数据挖掘与分析

学生在高职院校就读时，关于学生的课程成绩、图书借阅信息、网络在线学习时长、个人消费信息等会被学校各部门的信息系统记录，随着时间的推移，可以获取到学生在完整就读过程的详细数据，依据这些数据开展研究。本文主要分析两个问题：一是挖掘学生学习方式、升学形式对学业的影响，验证俗语“一分耕耘一分收获”；二是挖掘学生课程成绩间的相互关系，找出课程间的关联关系。

2.1 学生学业数据获取

本文的学生相关数据取自某高职院校教务管理系统和招就办相关数据系统中关于2015—2019级电子与信息工程系学生的各科课程成绩、在线网络平台学习时长、在线网络平台讨论次数、发帖数量、升学形式等信息。其中，针对问题一主要选取了2015—2019级电子与信息工程系学生大一到大二共4个学期中涉及线上线下混合型课程且课程线上学时一致的课程成绩计算加权平均值和学生在线网络平台学习时长、讨论次数、发帖数量以及升学形式、个人信息连接为一个综合数据集，共计2 133条信息。问题一部分原始数据如表1所示。针对问题二选取2015—2019级计算机应用专业学生大一到大二4个学期课程成绩，共计1 239条信息。问题二部分成绩信息如表2所示。

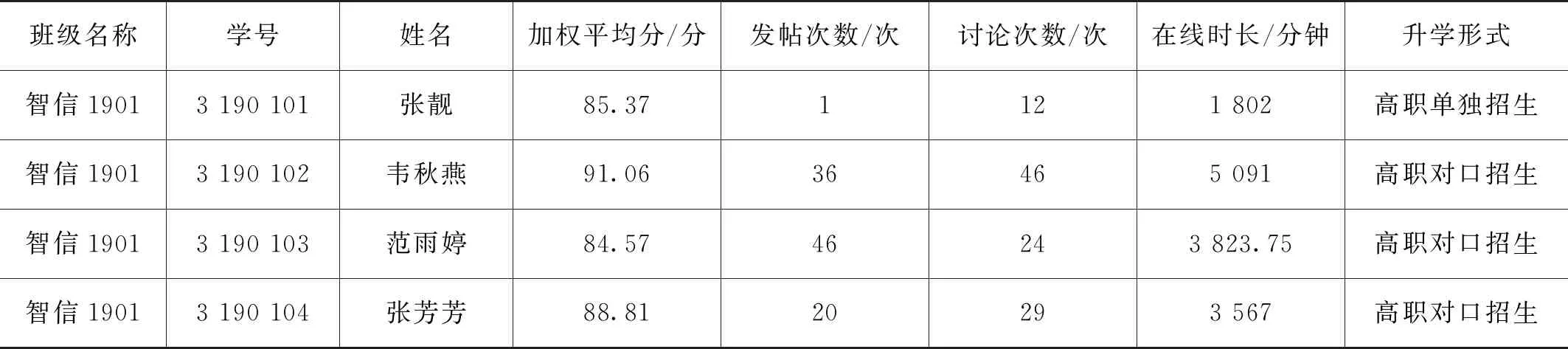
表1 问题一部分原始数据表

表2 问题二部分成绩信息

2.2 学生学业数据预处理

问题一和问题二中获取的学生数据有极小量学生因为退学、入伍、休学等原因，有一定缺失，对于这部分的数据条目将其删除，合并删除了与本文挖掘无关的学生学号与姓名。对有极个别因转专业，导致学生课程成绩缺少的现象，以该课程的成绩平均值进行了填充。问题二中涉及2015—2019级5届学生的成绩，因为每届学生的人培方案有一定区别，课程名称上有所区别，但是授课的主要内容一致，如2019级Java面向对象编程与2015级的Java程序设计、2019级PHP编程基础与2015级PHP程序设计实质为同一课程，对这类课程统一以2019级学生的课程名称进行统一，即将2015级的Java程序设计改为Java面向对象编程、2015级PHP程序设计改为PHP编程基础。因课程数量较多，本文主要选择了专业课。

针对问题一和问题二获取的数据，除学生升学形式以外，其余的数据为连续型数据，不适合接下来的Apriori算法挖掘，需要将其转化成为离散型数据。虽然选择的是线上学时一致的混合式课程，但是每位学生线上学习时长、讨论次数、发帖数量等数据均存在差异，如果使用基于确定值的区间划分方法，可能导致不同区间中数据不均匀的现象出现，同时也缺乏相应标准进行参考。此外，学生成绩由各科目授课教师批阅评卷而得，不同科目的难度不同且不同教师的评卷标准存在差异，如果按照传统的区间分布进行离散划分，即90～100为优、80～89为良、70～79为中、60～69为及格、60以下不及格，可能会导致各科目成绩分布不够均匀，一些课程的成绩在一个区间段较多，一些课程的成绩在另一区间段较多的问题。因而本文选用改进型KMeans算法对数据进行预处理。将问题一中线上学习时长、讨论次数、发帖数量、成绩加权平均值用KMeans算法按三类进行聚类后结果如图1—4所示。

图1 在线学习时长与人数直方

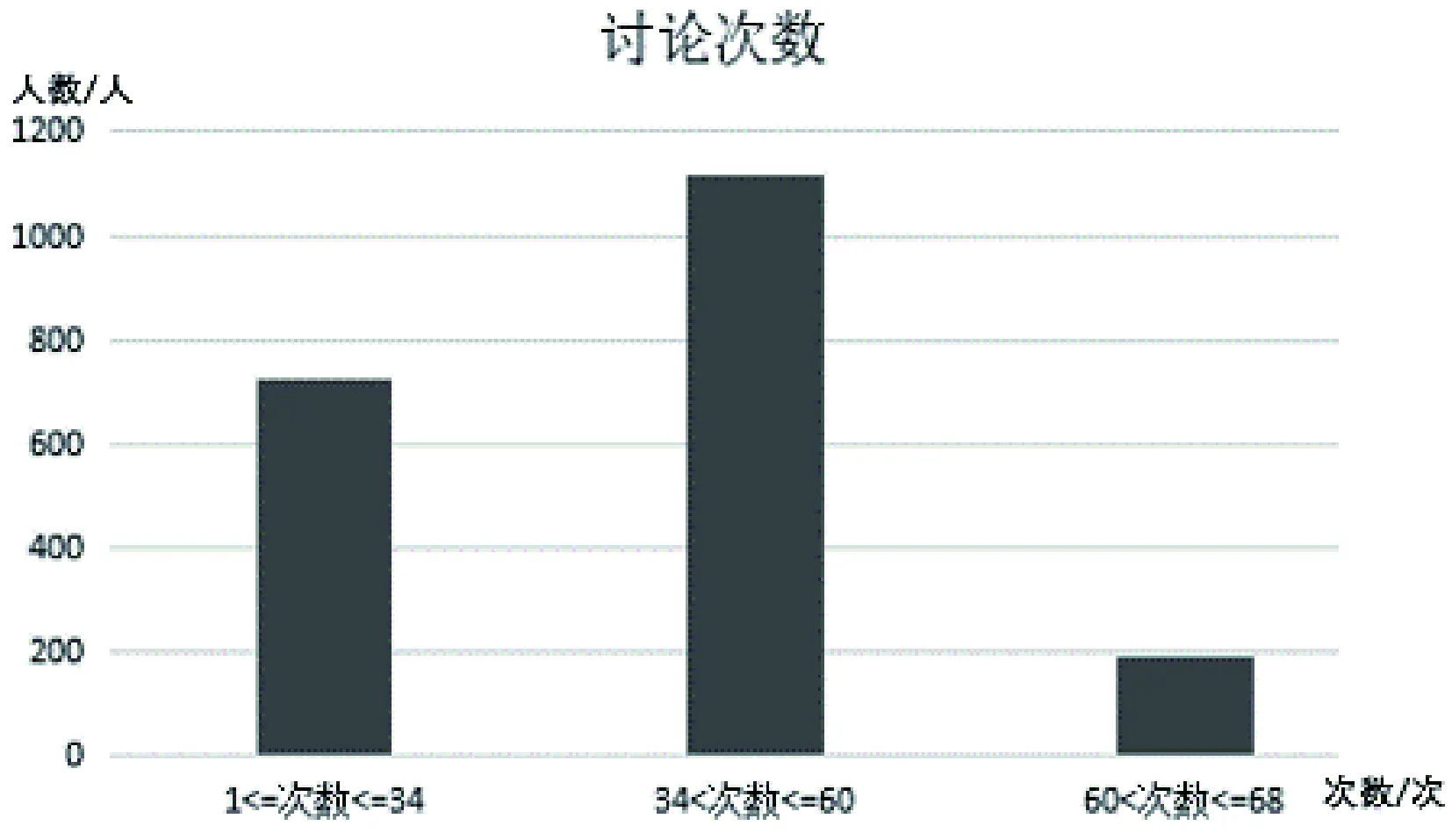
图2 讨论次数与人数直方

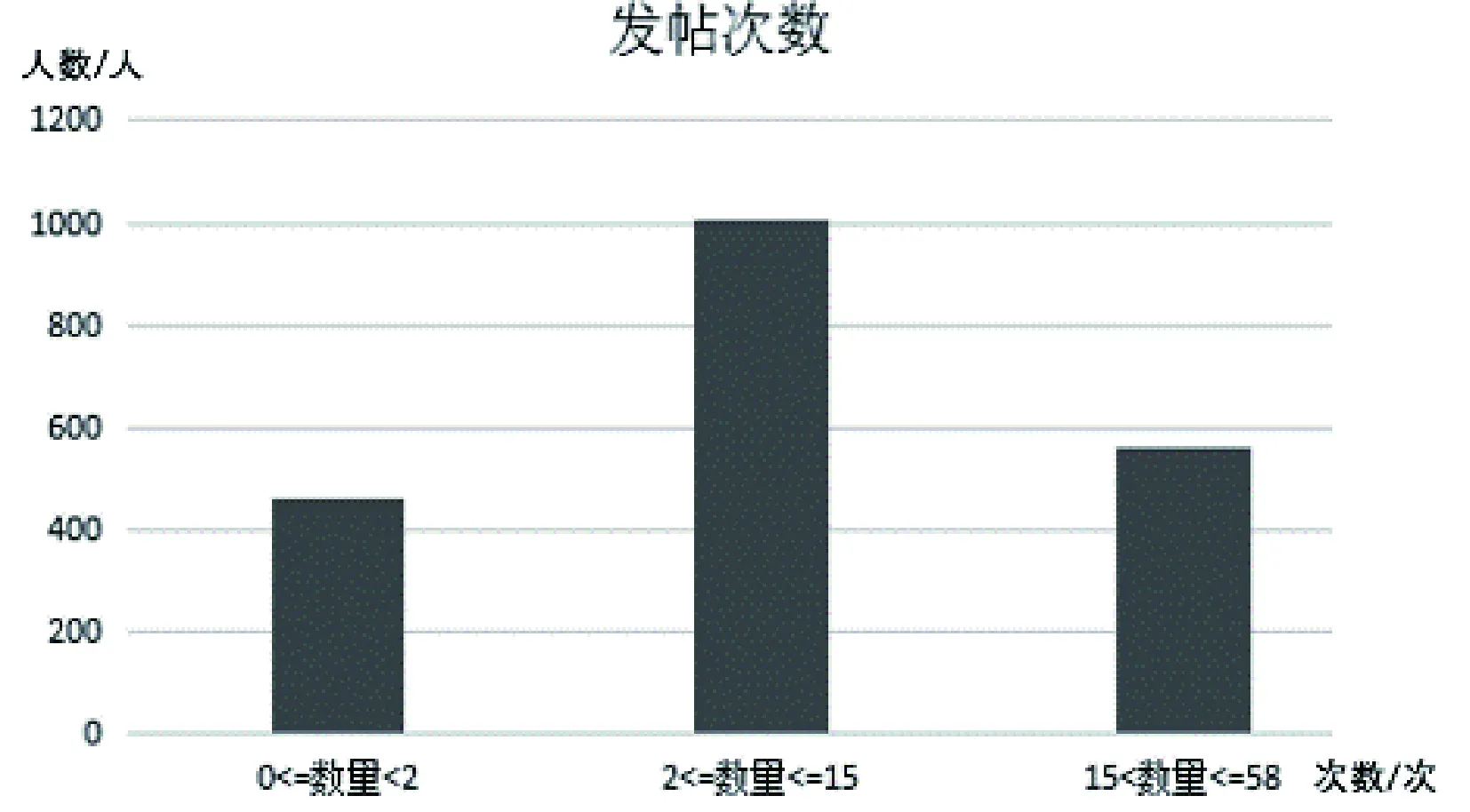
图3 发帖数量与人数直方

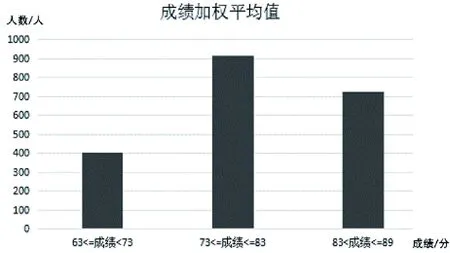
图4 成绩加权平均值与人数直方

其中线上学习时长的聚心分别为{1 341,3 723,6 933}，时长区间是[1 100,3 050),[3 050,6 000),[6 000,8 011]；讨论次数的聚心分别为{10,43,63},次数区间是[1,34],(34,60],(60,68]；发帖数量的聚心分别为{0.5,10,27},次数区间是[0,2),[2,15](15,58]；成绩加权平均值的聚心分别是{69,79,86},平均值区间是[63,73),[73,83],(83,89]。问题二中的专业课成绩也用KMeans算法进行聚类处理，选择按五类进行聚类，其中以“Java面向对象编程”课程为例的成绩点状图如图5和直方图如图6所示。“Java面向对象编程”课程的聚心是{62，69，78，85，90}，规定其所属等级从低到高分别为E、D、C、B、A，其中等级E对应区间[0,65]，等级D对应区间[66,73]，等级C对应区间[74,82]，等级B对应区间[83,88]，等级A对应区间[89,100]。用聚类处理后的不同聚心所属数据，特征更为明显，更易看出其中的差异。

图5 “Java面向对象编程”课程数据聚类结果点状

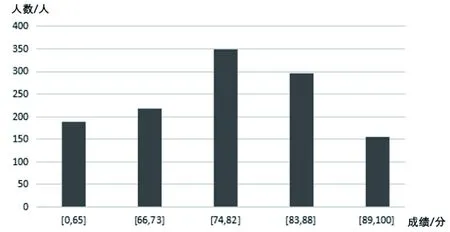
图6 “Java面向对象编程”课程数据聚类结果直方

2.3 学习方式对学习影响的挖掘与分析

用Apriori算法针对问题一，对离散化处理后的线上学习时长、讨论次数、发帖数量、成绩加权平均值以及升学形式进行挖掘，经过反复测试，将支持度设置为0.16，置信度设置为0.7，共挖掘出77条强规则，部分规则如表3所示。在线学习时长可以体现学生对学习的投入程度和自我管理能力；发帖数量体现学生在学习中发现问题、提出问题的能力；讨论次数反映学生对学习问题的主动解决能力和参与度；升学方式体现学生的来源；成绩加权平均值一定程度上体现了学生对知识的掌握程度。据此分析规则1—3，对于综合成绩处在中游的学生在学习过程中，学习时长可能不足，升学形式为高职对口招生与成绩中游有关系，可能是部分学生在中职阶段是计算机相关专业学生毕业生，因而具有一定基础，但其学习方式没有进一步提升，这部分学生的学习参与度相对积极，能主动解决问题并与同学们讨论分享，发现问题、提出问题的能力与成绩有较强关系，提升这部分学生对知识的进一步探索精神，加强学生的自我管理能力将有助于其提升成绩。分析规则4不难发现，对成绩处在下游的学生，与学习时长不足，学习参与度较低，发现问题能力较弱均有关系，调动他们的学习主动性，增加对学习的投入，提升其探索精神很有必要。分析规则5，对于成绩上游的学生不论是在学习时长、发帖数量、讨论次数上都超过成绩下游的学生，具备学习投入时间较长，积极参与学习讨论分享，主动发现问题、提出问题的能力较强等特点，证实了学习投入与学习产出成正比，验证了“一分耕耘一分收获”的说法。

表3 学习方式对学习影响部分强规则

2.4 课程间关联挖掘与分析

针对课程间关联挖掘，将Apriori的支持度设置为0.055，置信度设置为0.5，共有295条强规则，以“网页设计与制作”作前项为例，其相关规则如表4。

表4 以“网页设计与制作”作前项的关联规则

其中，规则6表明该课程直接影响到大二下学期的“移动应用交互设计”，该课程学习成绩为A的，“移动应用交互设计”成绩也为A，这和开发中网页设计作为移动应用的结构、样式基础有关系，前者的基础打好后对于后者取得好成绩有帮助。规则1、7、8、9、11、12、14、15、16是“网页设计与开发”与其他专业课联合影响“移动应用交互设计”，反映了移动应用是一门综合性课程，需要综合前、后端开发技术才能学好，前期课程学好了，学生的学习压力较小，能取得较好成绩，也反映了课程开设的渐进性，值得关注的是规则7，“技术实施框架”是C的情况下，只要网页设计是A，移动应用仍有可能是A，表明移动应用课程虽有前后端技术，但在考察时仍会相对注重前端的设计。规则2因数据库、网页设计与Linux系统的课程内容相对独立，通过提升度可看出，前两者对后者的正面影响并不是太大，前两门课程成绩一般，Linux系统成绩也一般可能是学生学习方法上的原因，与课程间关联较小。规则3、5网页设计、移动交互与富客户技术成绩好，软件工程成绩也好，软件工程主要任务是将复杂的客户需求描述成通过计算机编程可实现的计算模型，有了网页设计、移动交互与富客户技术的综合应用基础，对将客观世界的需求抽象描述成计算机模型的能力便能提升。规则4反映了数据库和网页设计成绩一般会导致移动互联网站设计成绩也一般的结果，移动互联网站设计考查学生前后端综合应用的课程，数据库相对是后端的内容，而网页设计是前端的内容，学生两门课都需要加强学习，才能提升移动互联网站设计的成绩。规则10中“网页设计与制作”和“网页编程”课程学习相对较好，“软件测试技术”成绩为A，反应前两门课程对网页开发中美观需求要通过反复耐心的修改和讨论才能实现，而软件测试中发现软件缺陷所需要的素质与细心、耐心、合作是一致的。规则13因“富客户端技术基础”开课在第3学期，移动应用交互开课在第4学期而无意义。

对“网页设计与制作”课程关联规则分析可知，“网页设计与制作”作为在大一上学期就开设的第一门编程类课程，该课程相对基础，对后期的网页开发类课程会产生较大影响，应加大对该课程的重视。教师应对该课程落后的学生给予积极的指导和帮助，避免学生因该课程没学好对后续学习造成不良影响，学生也应强化自己在该课程学习上的投入。

3 结语

高职院校在长期的信息化建设中，各部门的信息系统积累了大量有关学生的数据。本文获取了网络学习平台的学生在线学习时长、发帖提问数量、参与讨论次数和升学形式以及课程成绩。通过改进型KMeans算法对在线学习时长、发帖数量、讨论次数等没有明确基于数值区间划分标准的连续型数据进行了聚类，并对学生的成绩加权平均值和各科成绩分别进行聚类，减小了因为授课教师评分标准和课程难易度不同对成绩的影响，强化了不同成绩等级的特征。采用Apriori算法对聚类离散化处理后的在线学习时长、发帖数量、讨论次数、升学形式、成绩加权平均值进行挖掘，证实了学生学习努力与课程成绩成正比，验证了俗语“一分耕耘一分收获”的正确性，并对离散化处理后的各科成绩进行了挖掘，找出了课程间的关系，并以“网页设计与制作”课程为例进行了分析，对提升高职院校的教学方法与改善学生的学习方式提供了一定的参考。