工业微波加热腔的结构优化设计

周路人，秦 瑶，蔡成欣

(河南工业大学 信息科学与工程学院，河南 郑州 450001)

0 引言

微波加热具有加热效率高、能量利用率高和选择性加热等优势[1]，在食品、冶金、能源、医药、石油等工业领域有着广泛的应用。我国开始研究微波方面的应用工作从70年代开始。1994年，Sekkak等[2]人研究了圆柱腔体微波加热均匀性，使用FEM方法理论上探索腔体内部的电磁场分布情况。1996年，闫丽萍等[3]人研究了不同负载下微波加热输出功率的大小，研究结果表明微波加热载体形状、大小等因素会影响微波加热时的输出功率的值。2005年，雷文强等[4]人对实际应用中的微波炉腔体进行了建模仿真，仿真结果和实际生活中的实验对比，发现二者比较符合。后来，Bellanca等人为了求出微波腔体内部的场强分布情况，尝试使用时域有限差分法(Finite-Difference Time-Domain, FDTD)对微波加热腔体进行计算仿真。尽管他们的研究促进了微波加热方向的发展，但是他们并没有从根本上解决微波加热不均性的问题。

微波加热不均匀的问题在实际的加热过程中普遍存在。在微波加热过程中，由于微波具有选择性和穿透性的特点，在加热物质的过程中，容易引起加热物体内部出现温度过高的“热点”，而很多物质的微波吸收能力与温度呈正相关，这就使得温度高的区域对微波的吸收能力更大，反过来使得温度更高，进而引起热失控现象[5]。这种加热不均匀的问题会严重影响微波加热物体的品质和产量，更严重时会引起反应腔体的爆炸[6]。在加热微小颗粒的过程中，由于微小颗粒的互相积累，加热的物料区域存在一些狭缝或者尖锐位置，这些位置在微波能的辐照下很容易出现大于正常值的场强，危险的时候出现电打火现象[7]。这种现象的出现不仅影响产物的品质，还会引起安全事故，在一些燃点较低的物质，电打火的出现很容易引起重大的安全事故。为了工业微波加热安全的需要，降低安全事故发生的概率，研究解决微波加热不均匀的问题就显得非常迫切。本文从工业微波加热腔体形状、加热载体高度和激励源个数的角度出发研究了对微波加热均匀性的影响。

1 原理与方法

有限元算法广泛应用于热传导、电磁学和流体力学等工程问题，本文基于有限元算法开展对工业微波加热腔的优化设计，并通过有限元仿真软件COMSOL对所设计的器件进行建模和数值仿真。COMSOL软件以有限元方法为基础，利用数学方法去解决流体流动、热传导到结构力学、电磁分析等问题，可以通过利用COMSOL的数值仿真结果，去验证本文所提的有限元算法对微波加热均匀性研究是可行的和高效的。

微波加热的过程中，负载吸收微波能的大小和电场的平方成正比，而微波能吸收大小最直观的表现为温度高低，因此可以利用温度的均匀性去反映电磁场在微波加热腔中的分布均匀性。方差是概率论和数据统计中的一个重要参数，它衡量的是随机变量或者一组数据的离散程度，计算公式如公式(1)所示。

(1)

因此本文以温度数据的方差为参考标准来衡量微波加热的均匀性，以方差越低稳定性越好。

2 微波加热腔体的选择

当激励源个数为21，微波频率2.45 GHz，研究不同加热腔体在加热300 s后的加热均匀性。设计的模型形状分为长方形腔体、圆柱体腔体和梯形腔体，由于腔体高度为350 mm，本文将加热载体的位置放置0.05 m，0.1 m，0.125 m 3个高度，依次讨论在3个高度下的加热均匀程度。针对每一高度，提取加热负载的温度数据，利用Matlab计算该组数据的温度方差和平均温度，最后，计算出本高度的温度方差平均值和温度的平均值，以平均温度方差大小和总平均温度衡量微波加热的均匀性。

建模流程：在COMSOL软件里进行微波加热三维建模，首先设置建立腔体模型尺寸，选择对应的腔体材料和负载材料(负载选择的材料为水)；然后在电磁波频域里添加端口作为微波激励源，并进行网格划分，最后计算电磁场分布和温度分布。当激励源为21源情况下，模型具体参数如表1所示。模型仿真结果如图1—4所示。

表1 21源各模型参数

图1 长方体加热腔模型

图2 圆柱体加热腔模型

图3 梯形加热腔模型

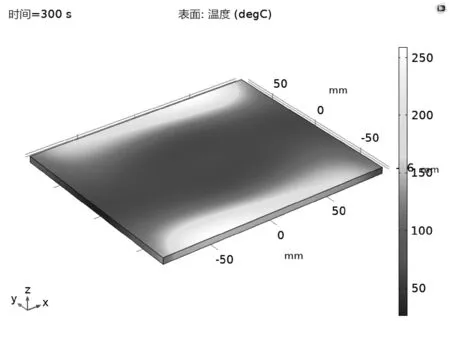
图4 长方体腔体加热负载加热300 s温度

仿真负载材料：水，相对介电常数取8-80j，仿真功率：1 000 W。激励源频率为2 450 MHz，功率为500 W，比热容(@65℃)为1.1 kJ/kg/K，导热系数(@61℃)为1.18 W/m/K。

当模型为长方体腔体时，依次提取加热载体的位置放置0.05 m，0.1 m，0.125 m 3个高度的温度数据图，数据结果如表2所示。

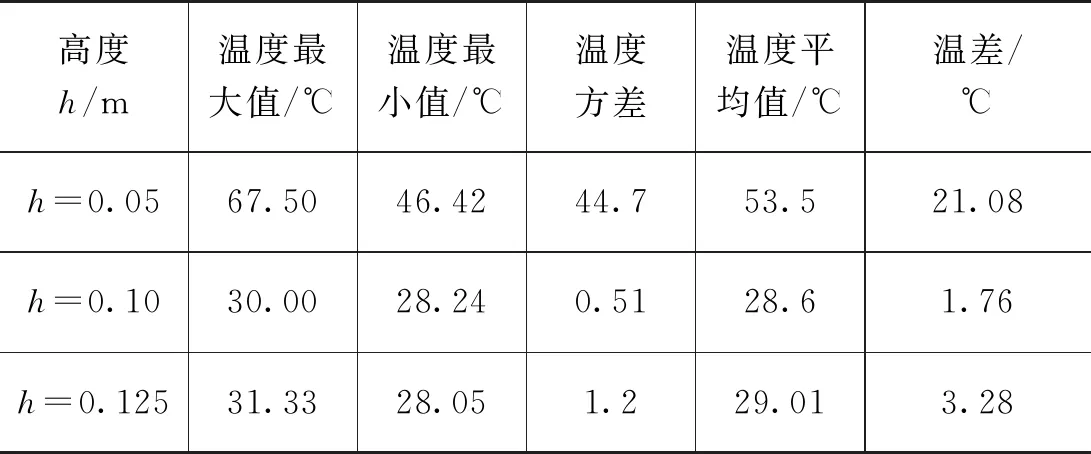
表2 长方体模型不同高度数据

可以看出，负载位于h=0.05 m时，加热载体最高温度达到230 ℃，最低温度大约50 ℃；负载位于h=0.10 m时，加热载体最高温度达到220 ℃，最低温度大约40 ℃；负载位于h=0.125 m时，加热载体最高温度达到215 ℃，最低温度大约30 ℃；加热载体的坐标系Y方向两边出现了“热点”，在位于加热负载的坐标系Y方向中间位置温度加热较慢，即出现了微波加热不均匀的现象。通过比较负载表面温度分布图和提取的温度数据发现负载高度h=0.10 m的加热情况明显好于h=0.05 m和h=0.125 m的情况。为了综合考虑该模型的加热均匀性，笔者把3个高度的方差的平均值作为微波加热均匀性的参考指标，经过求解得到的方差均值为15.47。

当模型为圆柱体时，依次提取加热载体的位置放置0.05 m，0.1 m，0.125 m 3个高度的温度数据图，数据结果如表3所示。

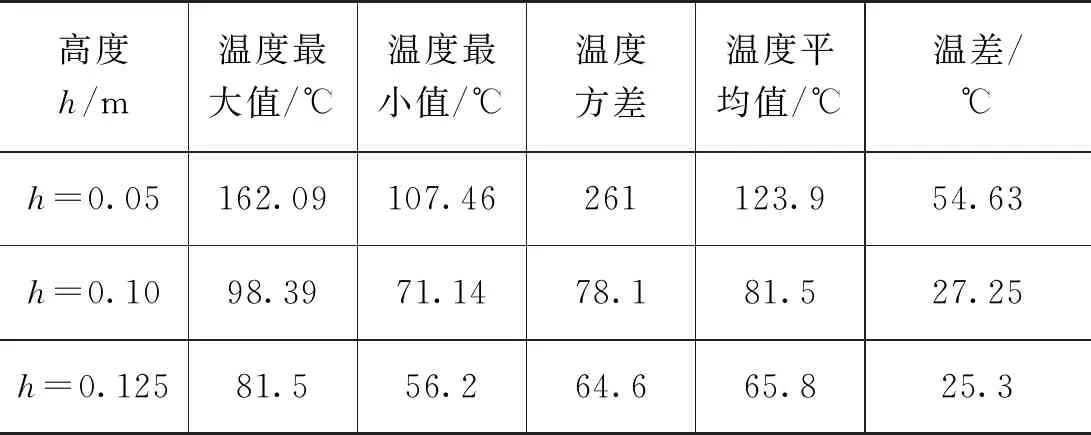
表3 圆柱体模型不同高度数据

从圆柱体腔体仿真所得到的温度分布图可以看出，负载位于h=0.05 m时，加热载体最高温度达到350 ℃，最低温度大约40 ℃；负载位于h=0.10 m时，加热载体最高温度达到270 ℃，最低温度大约40 ℃；负载位于h=0.125 m时，加热载体最高温度达到225 ℃，最低温度大约30 ℃；加热载体坐标系的X方向两边出现了“热点”，在位于加热负载坐标系的X方向中间位置温度加热较慢，即出现了微波加热不均匀的现象，通过比较负载表面温度分布图和提取的温度数据发现负载高度h=0.125 m的加热情况明显好于h=0.05 m和h=0.10 m的情况，为了综合考虑该模型的加热均匀性，笔者以3个高度的方差的平均值作为加热均匀性指标，经过求解得到的方差均值134.9。

当模型为梯形腔体时，依次提取加热载体的位置放置0.05 m，0.1 m，0.125 m 3个高度的温度数据表，数据结果如表4所示。

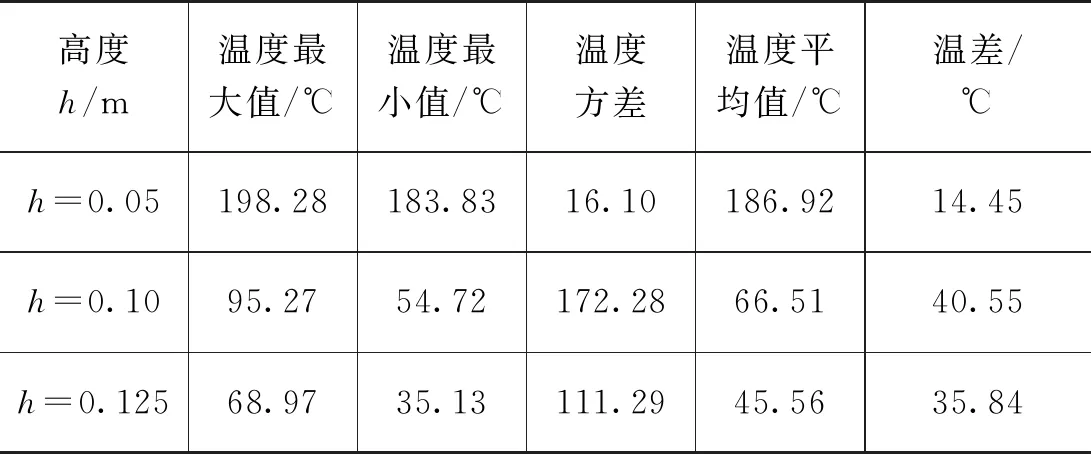
表4 梯形模型不同高度数据

从梯形腔体仿真所得到的温度分布图可以看出，负载位于h=0.05 m时，加热载体最高温度达到235 ℃，最低温度大约80 ℃；负载位于h=0.10 m时，加热载体最高温度达到225 ℃，最低温度大约35 ℃；负载位于h=0.125 m时，加热载体最高温度达到185 ℃，最低温度大约30 ℃；加热载体坐标系的X和Y方向两边均出现了“热点”，在位于加热负载坐标系的X和Y方向中间位置温度加热较慢，出现了微波加热不均匀的现象，通过比较负载表面温度分布图和提取的温度数据发现负载高度h=0.05 m的加热情况明显好于h=0.10 m和h=0.125 m的情况。为了综合考虑该模型的加热均匀性，笔者以3个高度的方差的平均值作为加热均匀性指标，经过求解得到的方差均值99.89。

最后，计算3个高度的方差均值，长方体模型方差均值为15.47，圆柱体模型方差均值134.9，梯形模型方差均值为99.89。经过比较，长方体的方差均值最小，因此认为长方体腔体的加热均匀性更好。

3 最佳负载的高度选择

当模型选择为长方体时，模型如图5所示。长方体腔体内设置加热负载高度依次是h=0.06 m，0.08 m，0.1 m，0.12 m，0.14 m，0.16 m，针对每一高度，在加热负载的X方向、Y方向上按照一定间距各取10条线，并且提取出每一条线的温度数据，温度数据如图6所示。利用Matlab计算每一条线的温度方差和平均温度，最后，计算出本高度的温度方差平均值和温度的平均值，以温度方差平均值大小和总平均温度衡量微波加热的均匀性。通过对每个高度进行数据提取和处理得到数据如表5所示。

表5 长方体模型不通高度数据

图5 长方体模型负载截线

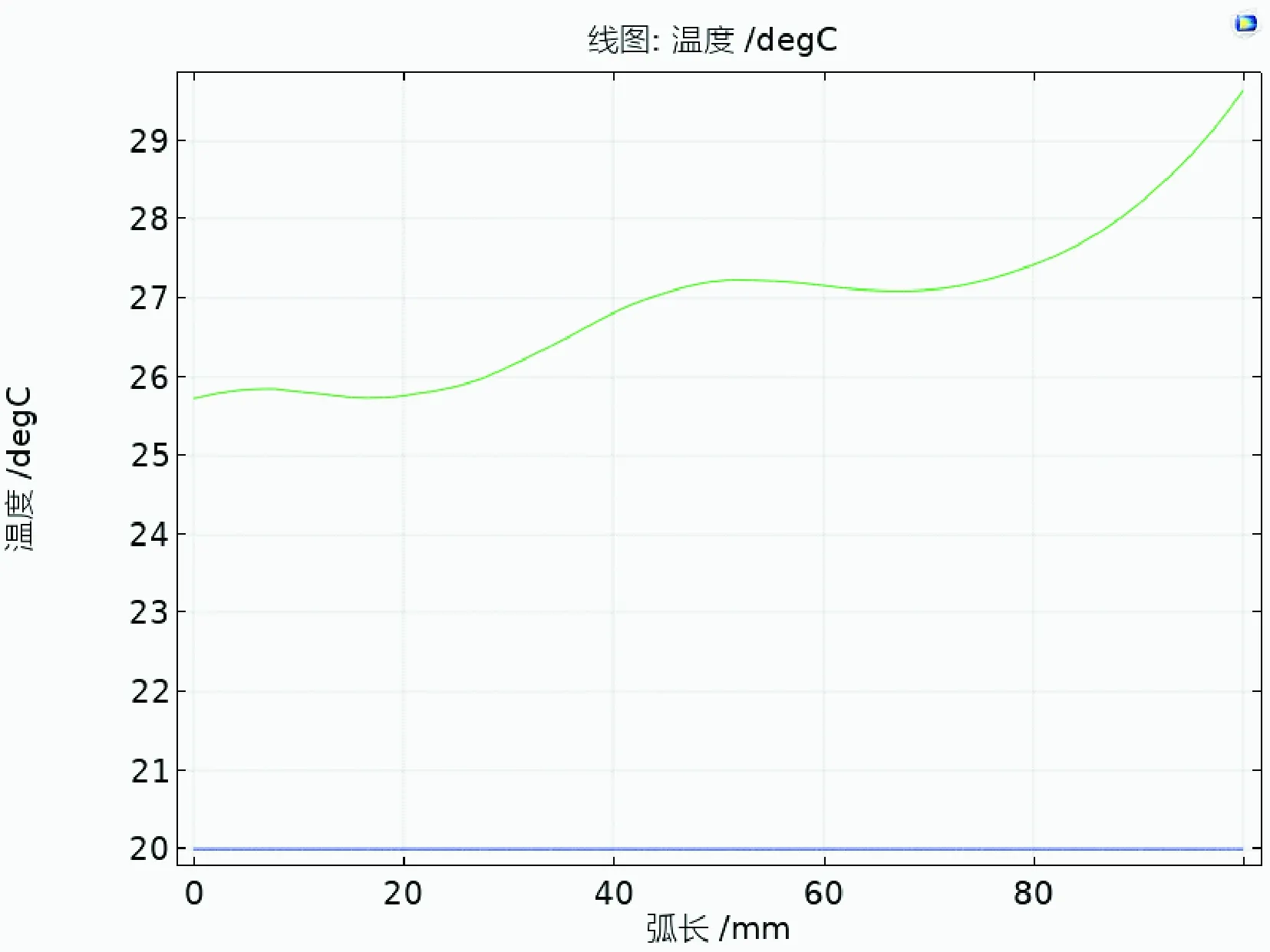
图6 长方体模型负载截线温度

从仿真结果来看，负载的高度的确会对加热均匀性有一定影响，随着高度的增加，方差值变得越来越小，通过比较h=0.06 m，0.08 m，0.1 m，0.12 m，0.14 m，0.16 m的方差均值数据，负载高度h=0.16 m的方差平均值最小，负载高度h=0.06 m时方差平均值最大，仅仅从方差平均值考虑认为h=0.16为最好，如果到把方差大小和平均温度结合起来考虑，认为h=0.12 m使得高度为最佳高度，即当高度h=0.12 m时的加热均匀性最好，在确定了最佳高度后，接下来将对激励源个数对微波加热均匀性的影响展开了研究。

4 激励源个数对微波加热均匀性的影响

根据前面仿真结果，模型选择为长方体模型，负载高度选择为h=0.12 m，对激励源个数为21个、19个、15个分别进行仿真，研究模型如图7—9所示。对位于XY平面的负载进行沿X方向和沿Y方向各取10条温度数据，利用Matlab进行数据处理得到方差，最后计算两个方向的方差值，分别如图10—12所示。

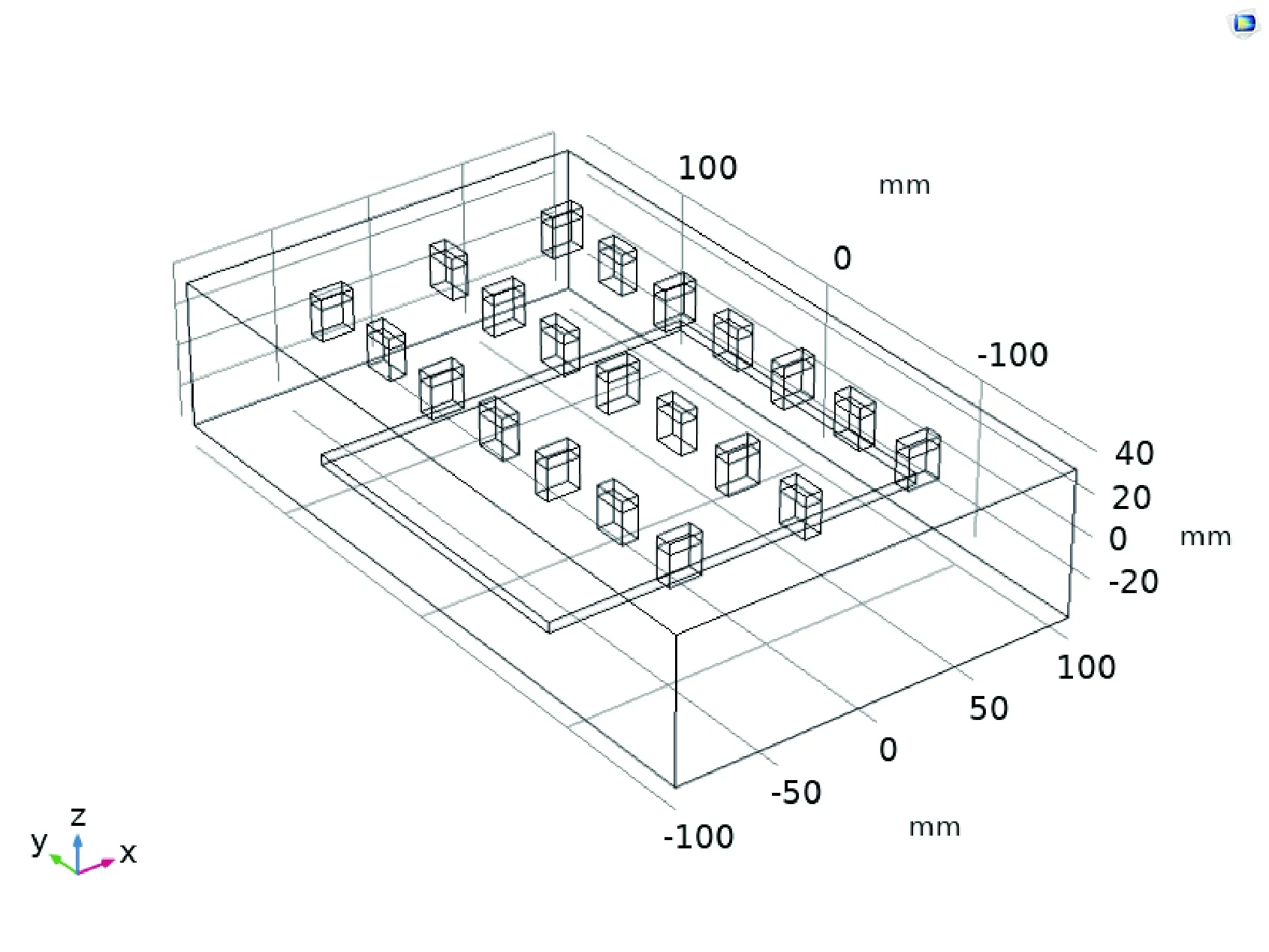
图7 21源负载高度h=012 m长方体模型

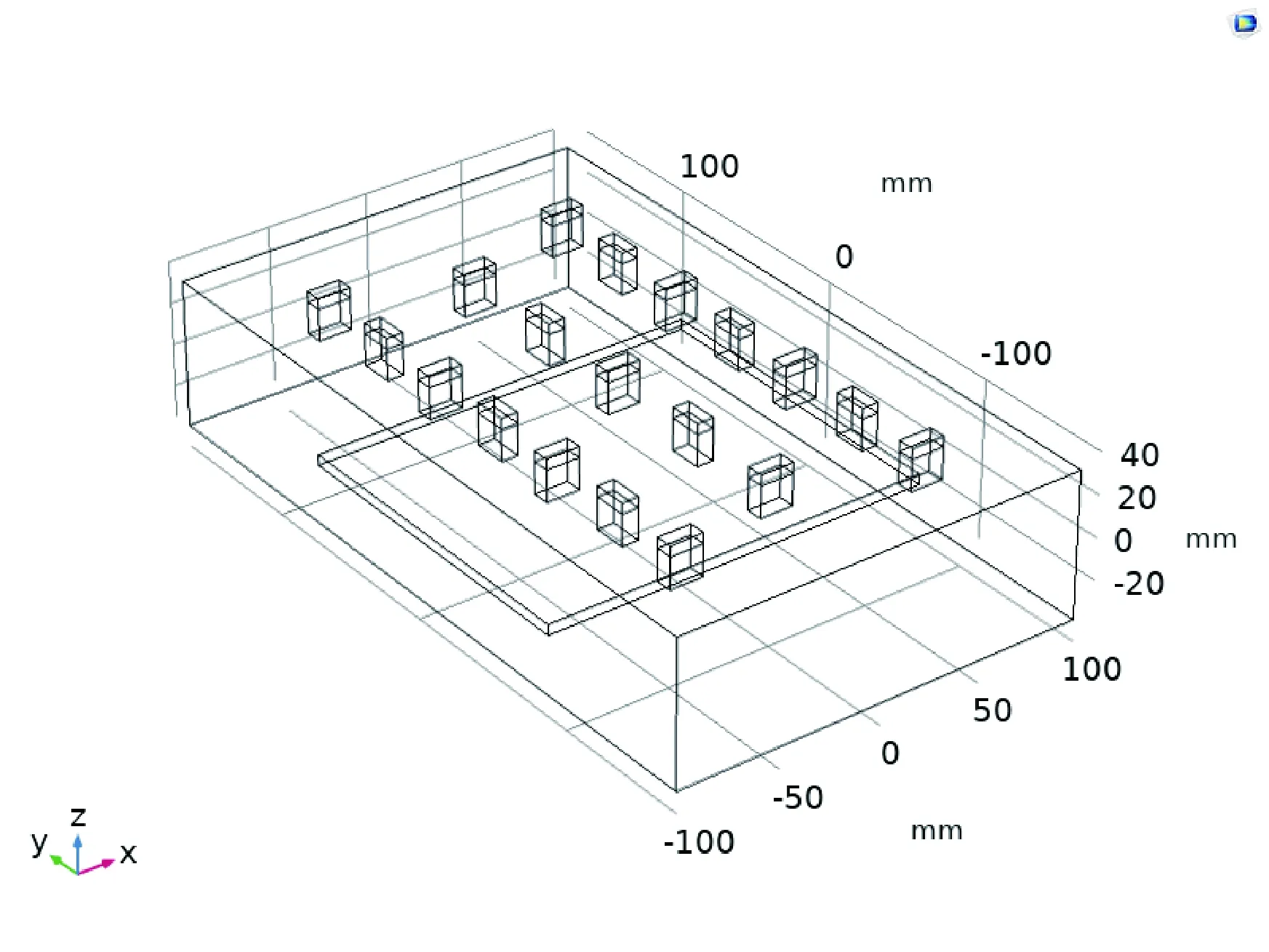
图8 19源负载高度h=012 m长方体模型

图9 15源负载高度h=012 m长方体模型

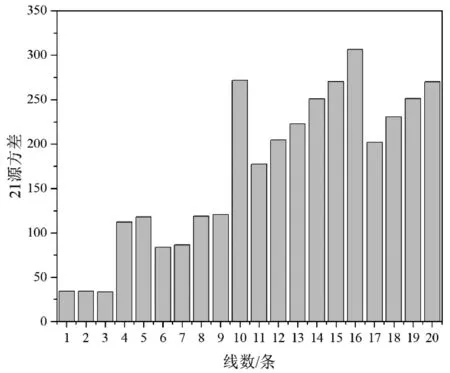
图10 21源方差图

从仿真结果来看，激励源个数为21个、19个和15个时，方差平均值分别为169.99，153.3和125.97。15源的方差平均值是三者中最低的。从得到的3组数据可以分析出激励源越少方差平均值越小，即加热均匀性越好，经比较发现15源的加热均匀性更好。

5 结语

本文研究了加热腔体形状、加热载体的高度和不同激励源个数对微波加热均匀性的影响，并进行了建模与仿真。根据仿真结果，发现长方体模型的均匀性更好；在确定以长方体为参考模型情况下，比较了负载处于不同高度的方差均值和温度平均值，发现当负载高度h=0.12 m时的均匀性更好；当确定了模型为长方体，负载高度h=0.12 m条件下，比较了激励源个数对微波加热均匀性的影响，实验结果发现19源的加热均匀性比21源的情况好；15源的方差总平均值为125.97，是三者中最好的。本文对研究微波加热均匀性和有效性具有的一定的指导意义。

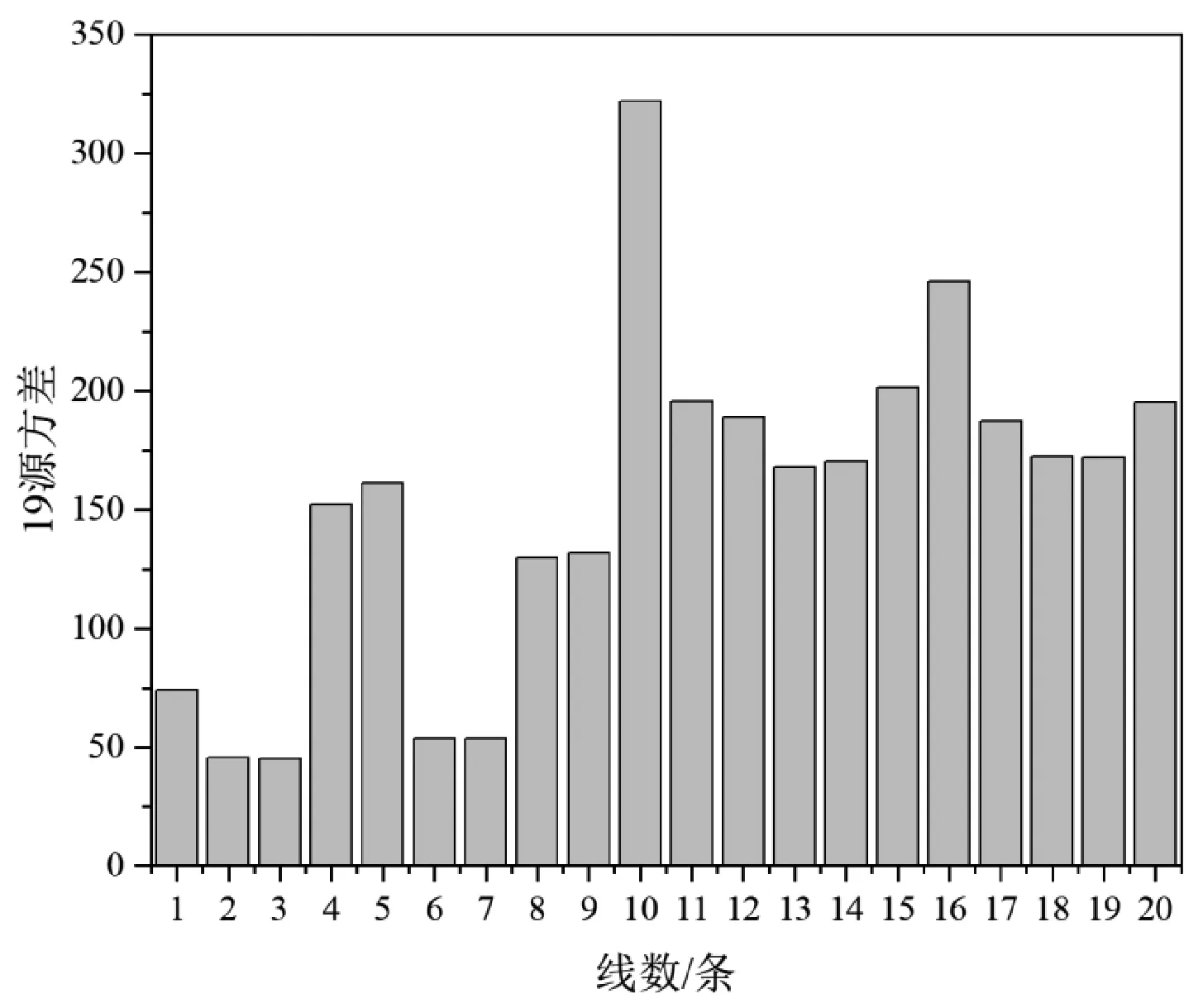
图11 19源方差图

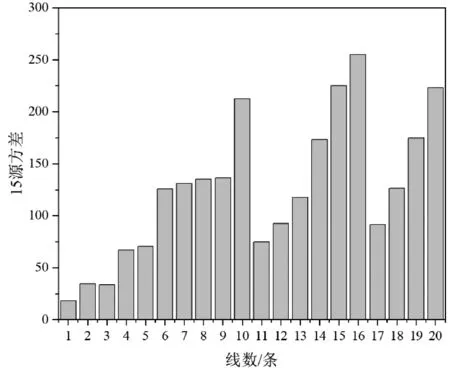
图12 15源方差图