基于主电流控制的并联DC-DC升压变换器改进

范 璟

(西安文理学院 机械与材料工程学院，西安 710065)

0 引言

与单一、大功率、集中式功率变换器相比，并联低功率变换器具有许多优点，其中一些优点与系统性能有关，例如更高的效率、更好的动态响应和更好的负载调节。对于并联DC-DC变换器的运行，传统的下垂方法提供了真正的冗余，因为模块之间没有互连。然而，有效的负载均流和电压调节是下垂法的主要缺点。文献[1]提出了一种新的下垂方法，通过自适应调节参考电压来改善负载均流，并可适当调节输出电压。并联变换器中的输出电压变化是由各种条件引起的，例如负载、输入功率的变化或电压反馈信号中的测量误差。一般情况下，模块之间的循环电流可能是由输出电压中的小失配引起的，这导致模块之间的负载电流分配不相等[2]。文献[3]提出了一种改进的下垂控制器，以克服由于电压反馈信号测量误差而导致的输出电压失配。变换器之间的循环电流测量用于修改标称电压，从而减小模块输出电压的误差。

并联变换器的工作点是随机修改的，因此必须重新计算一组新的控制器参数。为了克服这一问题，文献[4]提出了buck变换器并联控制方案，对两个并联变换器在暂态和稳态下的控制性能进行了验证。两个模块采用交错运算方式，通过将两个模块的斜坡信号相移半个周期来实现。

主从式电流控制是并行变换器有源电流共享控制的常用方法之一，它使用模拟无线通信或变换器之间的内部通信链路。文献[5]利用模拟无线通信实现了并行变换器的主从式电流共享控制，它使用一个变换器作为主控制器。所选变换器在电压控制模式下工作，以调节跟踪参考电压的输出电压。其他变换器在电流控制模式下工作，以调节其输出电流。由于主控制器根据总负载电流获得其参考电流值，所以这些变换器作为从控制器工作，从变换器通过高速通信链路接收新的参考电流[6]。为了减小时延，提高系统性能，采用了变换器之间的高速通信方式。在某些电源应用中，带有连接线的模拟控制器会产生噪声，这使得它仅适用于变换器彼此靠近的低功率应用[7]。

本文通过模块间的通信链路，实现了并联变换器的同步切换。提出的基于主电流控制的并联DC-DC升压变换器控制方法可以在负载变化时同步输出电压，该方法采用线性控制，以电压控制方式作为外环控制两个并联变换器，并调整其参考电压。算法的输入是来自并联变换器公共直流母线的电压测量和一个变换器的电流测量(主电流)。然而，电流内环控制将选择的电流测量值作为两个控制回路的反馈电流信号，因此，基于下垂法实现了负载均流。由于并联变换器的控制回路具有相同的时延，因此并联变换器的输出电压电平是同步变化的，这确保了在负载变化期间，输出电压没有失配，也没有循环电流，此外还可以最小化输出电流波形中的纹波。

1 DC-DC升压变换器设计

一般情况下，并联直流升压变换器输出电压电平不匹配都可能引发循环电流。为避免循环电流的产生，可使用并联DC-DC升压变换器的同步开关[8]。同步开关迫使并联变换器仅在两种工作模式下工作，由此可确保并联变换器的切换是同步的，两个并联MPPT模块之间没有相互通信链路，两个具有单个MPPT的并联260 W光伏组件不存在同步切换[9]。两个MPPT模块的输出与负载并联，每个模块的电流测量结果如图1所示。

图1 两个并联MPPT模块的输出电流

从图1可以看出，当一个开关在一个并联的MPPT模块中闭合时，另一个MPPT模块的电流同时增大，反之亦然。DC-DC升压变换器的等效电路如图2所示。DC-DC升压变换器电路由直流电源、电感、MOSFET开关、二极管、电容和负载电阻组成。

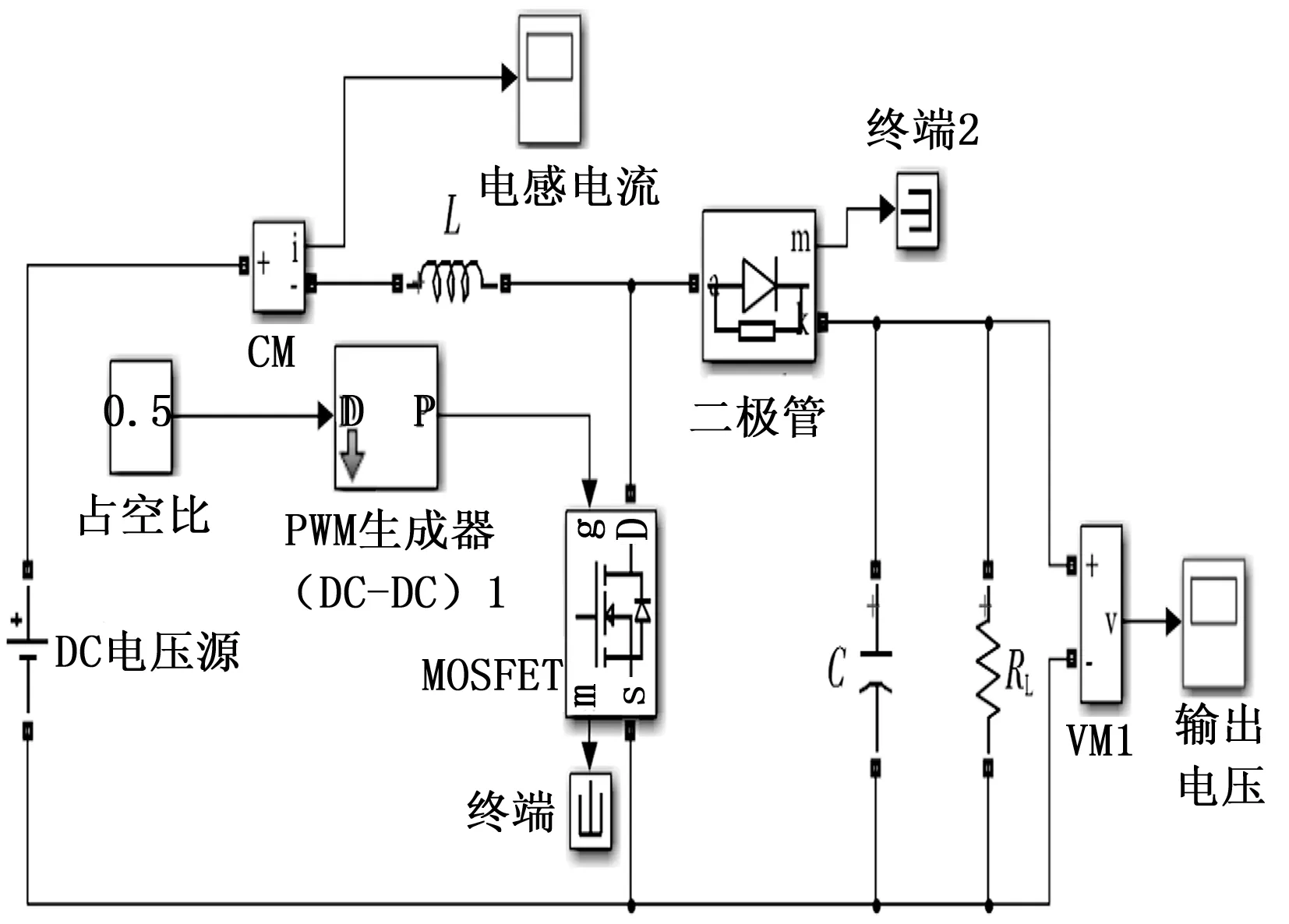
图2 DC-DC升压变换器

从运行角度来看，DC-DC升压变换器可以在连续导通模式(CCM)和不连续条件模式(DCM)下工作，运行模式取决于变换器的参数[10-12]。对于连续导通模式，升压变换器的参数(例如电容C、电感L和占空比D)可以通过下式获得：

(1)

(2)

(3)

其中:纹波极限(δ)为1%。升压变换器参数如表1所示。

表1 升压变换器参数

2 PI控制器设计

通过考虑连续导通模式，升压变换器在两种状态(ON/OFF)之间切换。PWM占空比为0.5时的电感电流(IL)和输出电压(Vout)波形如图3所示。

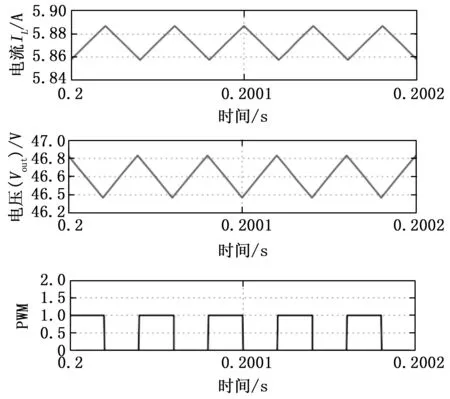
图3 CCM中的电感电流(IL)波形和输出电压(Vout)波形

如图3所示，在导通(ON)状态下，电感电流增加，但输出电压降低。对于关断(OFF)状态，MOSFET开关被打开，导致电感电流减小和输出电压增加[13-14]。在一个周期(ON和OFF状态)内，采用状态空间平均技术[15-16]，其表达式为：

(4)

(5)

对于小扰动，使用标准线性化技术[17]，如下所示：

(6)

在小信号分析中，输入电压是恒定的。DC-DC升压变换器的小信号模型可由下式给出：

(7)

(8)

外环和内环的传递函数分别给定为:

(9)

(10)

外环控制器和内环控制器可以采用Ziegler-Nicholas、环路成形法和频率响应法来设计PI控制器。然而，为了简单起见，使用Matlab/Simulink中的Sisotool来调整控制器并评估稳定性的适用性[18-20]。对于外环，在控制系统工具箱中使用传递函数的Sisotool命令为伯德图和根轨迹提供图形用户界面。

升压变换器的根轨迹在右z平面中的零点不会影响系统的绝对稳定性。通过修改反馈控制器的零极点模式，可以改变闭环频率响应，直到获得期望的静止状态。为了确定外环控制器增益，在线修改了根轨迹的位置。表2给出了外环比例和积分控制器的增益。类似地，Sisotool命令用于内环传递函数，为根轨迹和伯德图生成图形用户界面。

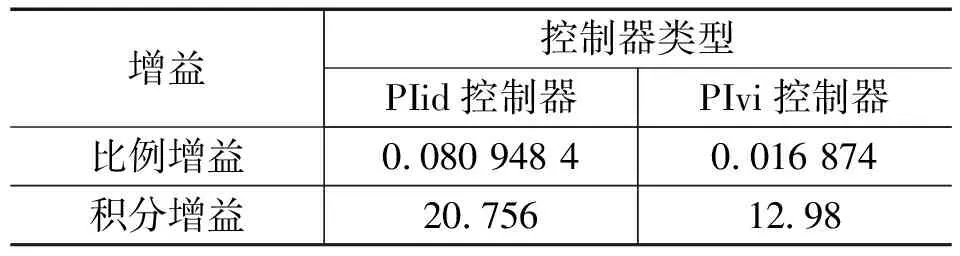
表2 升压变换器PI控制器参数

3 拟用方法

两个并联DC-DC升压变换器的原理图如图4所示。图4中的两个并联DC-DC升压变换器连接到一个公共直流，负载直接连接到公共直流母线。变换器I1和变换器I2的输出电压和电流分别为V1，I1和V2，I2。由于变换器I和变换器I2接在共同的直流母线上，所以输出电压V1和V2是相等的。因此，每个变换器的输出电压等于负载电压，负载电流等于两个变换器的输出电流之和。

图4 两个升压并联变换器的原理图

图4中的零循环电流可以通过负载或输入功率变化期间输出电压的零失配来实现。该方法根据下垂法调整参考电压，保证了输出电压电平的同步。每个变换器的外部电压回路调节输出电压，输出电压将处于调整后的参考电压水平。内部控制回路使用一个变换器的测量电流信号作为并联变换器的反馈电流信号(主电流控制)，内部电流回路需要模块间的互连电流测量。然而，为了克服输出电压的失配，该算法被用来调整并联变换器的参考电压。图5所示为下垂法的一般负载调节特性。

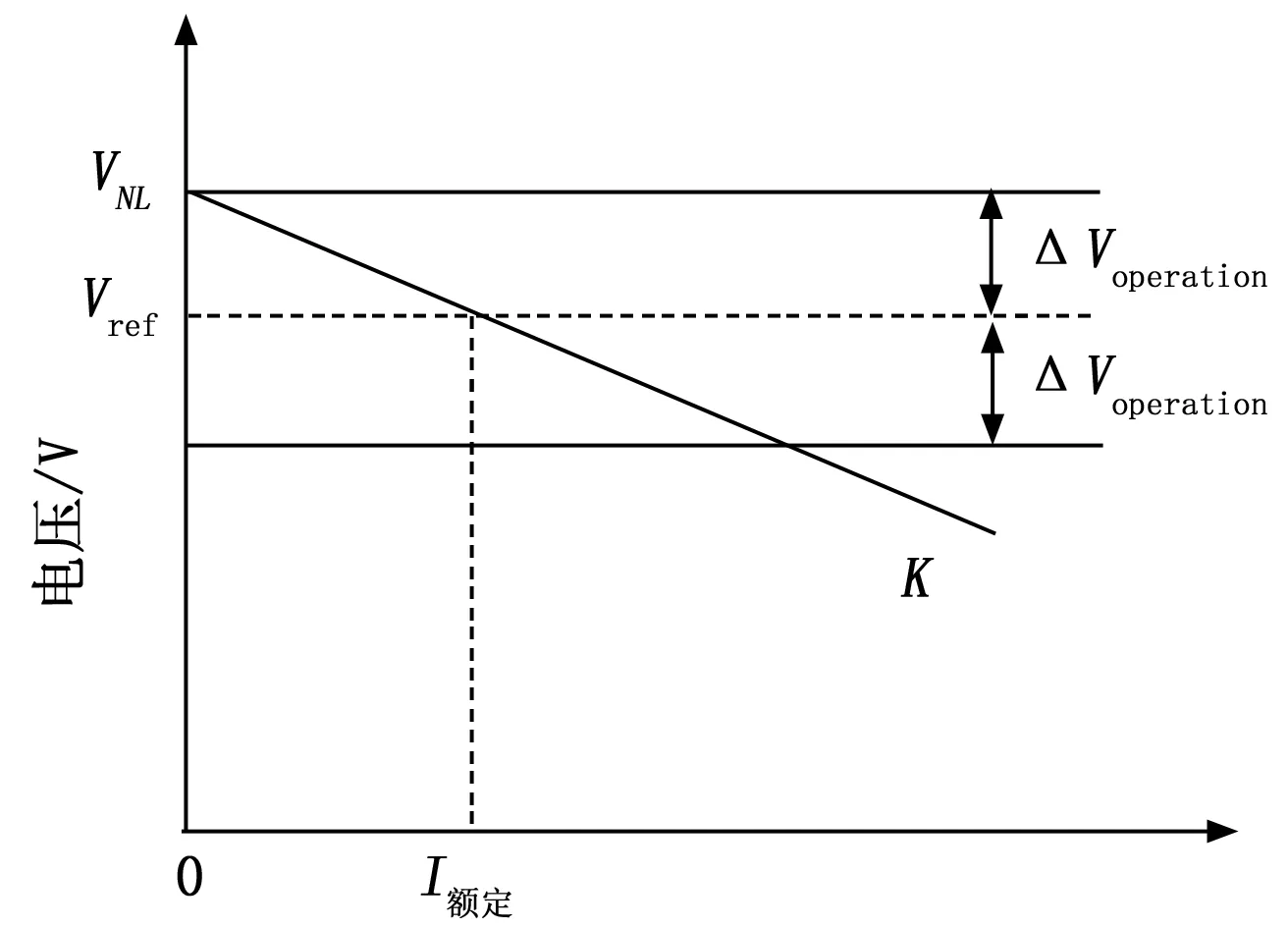
图5 下垂法的负载调节特性(增益为K)

如图5所示，VNL为空载电压，Vref为参考电压(额定工作电压)，ΔVoperation为允许算法调整参考电压的电压范围，K为其中一个变换器的下垂增益。因此，如果输出电压不在工作电压ΔVoperation范围内,则参考电压为常数，等于变频器的额定电压。从图5可以看出，随着输出电流增加，输出压降Vout可表示为式(11)：

Vout=VNL-K×Iout

(11)

其中:Vout为直流母线的输出电压，Iout为其中一个并联变换器的输出电流。

基于主电流控制的改进下垂方法的输入是在公共母线上测量的输出电压、其中一个变换器的输出电流和参考电压，所选变换器的负载调节特性用于在负载变化期间调整参考电压。该算法的第一步是检查输出电压是否在算法的工作区内。如果绝对值ΔV大于ΔVoperation，则将ΔVref设置为零，并且参考电压保持在其额定值。然而，如果绝对值ΔV不大于ΔVoperation,则将所选变换器的输出电流与下垂电流(Vdroop)进行比较，根据所选变换器的负载调节特性计算下垂电流，如式(12)，式(13)：

(12)

ΔIdroop=Idroop-Iout

(13)

ΔVdroop是计算出的下垂电流与所选变换器电流的实际测量值之间的差值。如果绝对值ΔIdroop不大于公差误差(1*-15)，则工作点将与基于所选变换器的负载调节特性计算出的工作点相同，因此，参考电压将保持在其额定值。然而，如果绝对值ΔIdroop大于公差误差(1*-15)，则参考电压将根据所选变换器的负载调节特性进行调整，式(14)，式(15)：

Vdroop=VNL-Vout×K

(14)

ΔVref=Vref-Vdroop

(15)

ΔVref是参考电压与根据所选变换器的负载调节特性计算出的下降电压之间的差。如果ΔVref为正值，则将其从参考电压中减去，这意味着需要根据下垂法的负载调节特性来降低输出电压。相反，如果ΔVref为负值，则将其添加到参考电压中，以增加输出电压电平。

4 仿真结果与讨论

为了验证提出方法的有效性，通过Matlab/Simulink进行了仿真实验，步骤如下。

步骤1：打开Matlab软件，选择Simulink。

步骤2：进入Simulink界面，点击库浏览器。

步骤3：打开库浏览器，选择用于建立仿真模型的设备及器件等模块。本文中的仿真分为两种：第一种情况下，考虑了两个并联升压变换器在功率级不匹配或零失配的情形；第二种情况是功率级失配为DC-DC升压变换器的10%。将表2中的PI控制器参数作为Matlab/Simulink模型的输入参数。

步骤4：将步骤3中的模块拖入Simulink仿真模型中。

步骤5：选择Scope进行波形显示。

步骤6：运行仿真程序，观察仿真结果。

步骤7：改变算法中的参数，重复步骤3～步骤6，以此对仿真结果进行比对，从而得出结论。

图6所示为两个相同并联DC-DC变换器的下垂特性。由于两个变换器的下垂增益相等，因此负载电流共享相同，两个变换器具有相同下垂增益的主要原因是它们的功率级均不存在失配。在不同的输出电压水平下，两个变换器的输出电流将被均等地共享。

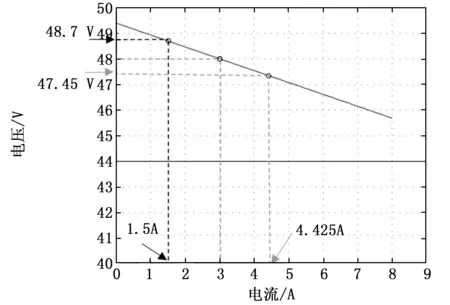
图6 两个变换器的下垂方法负载调节特性(零失配)

4.1 并联升压变换器功率级不匹配

在第一个检查的情况下，通过在0.2 s处增加并联电阻，负载从16 Ω变为8 Ω，负载电阻在0.4 s时进一步从8 Ω降低为5.33 Ω。图7所示为共同直流母线的输出电压。

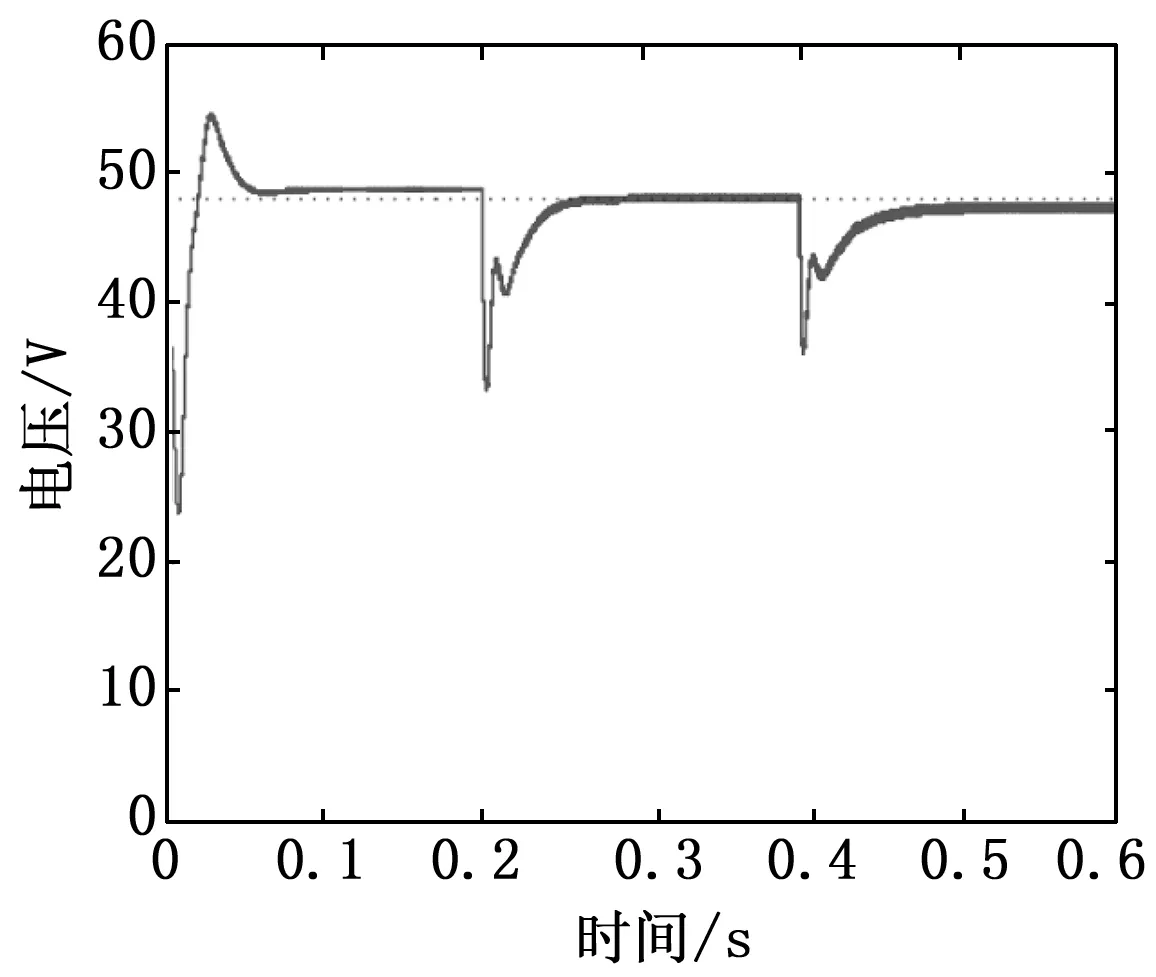
图7 直流母线的输出电压

图7中的输出电压根据下垂法的负载调节特性，由所提出的算法进行调整。该算法在负载变化时调整参考电压，并实现并联变换器输出电压电平的同步。因此，根据两个变换器的相同负载调节特性，负载电流分配将相等，每个变换器的输出电流和总负载电流如图8所示。

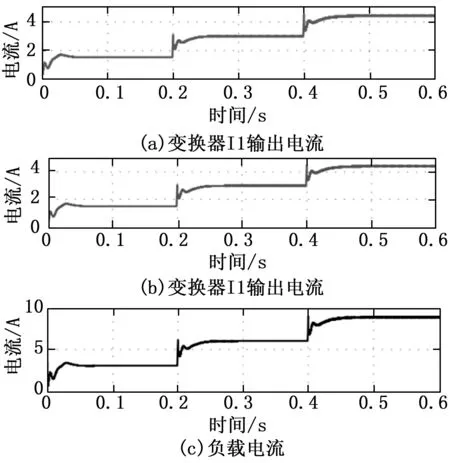
图8 无不匹配情况下模拟结果的输出电流

4.2 并联升压变换器功率级失配10%

当负载电阻为16 Ω时，本文算法根据下垂法调整参考电压。由于负载电阻值为16 Ω,所以算法将输出电压电平调节为48.7 V，各变换器输出电流为1.5 A。此外，当负载在0.2 s内从16 Ω变化为8 Ω时，算法根据负载电阻的新变化调整基准电压。输出电压电平变为48 V，每个变换器的输出电流为3 A，时间介于0.2 s至0.4 s之间。当负载电阻进一步降低到5.33 Ω时,算法将输出电压电平调节为47.4 V，每个变换器的负载电流共享为4.425 A。在负载调节特性不失配的情况下，所提出的方法可以同步调节输出电压电平，从而不会导致输出电压不匹配，因此不会产生循环电流。表3给出了功率级失配为DC-DC升压变换器的10%变换器的参数。

表3 升压变换器的工作值

图9所示为第二种情况，两个变换器的负载调节特性不匹配达到10%。

图9 两个变换器的下垂方法负载调节特性(10%不匹配)

从图9可以看出，两个变换器之间的负载电流分配不相同，这是因为两个变换器的负载调节特性不匹配达到10%，两种变换器的下垂增益是不同的。与第一种情况相似，在0.2 s时，负载电阻由16 Ω变为8 Ω，在0.4 s时，负载电阻由8 Ω进一步减小为5.333 Ω。下垂法负载调节特性失配10%的公共母线输出电压如图10所示。

图10 直流母线上的输出电压(10%不匹配)

从图10中可以看出，本文算法根据两种变换器的负载调节特性调整参考电压，并表明输出电压是根据负载电阻的变化而调节的,每个变换器的输出电流和负载电流如图11所示。

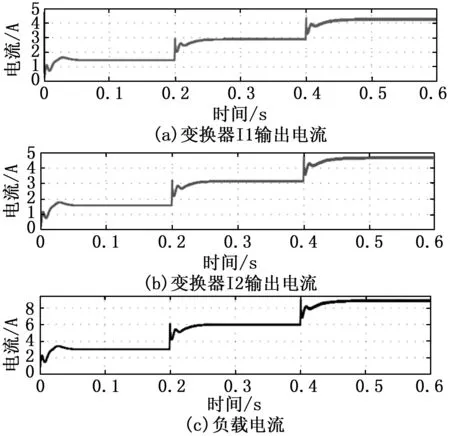
图11 仿真结果输出电流(10%不匹配)

当负载电阻为16 Ω时，调节后的输出电压为48.7 V，变换器I1和变换器I2的负载共享电流分别为1.4 A和1.6 A。由于负载电阻在0.2 s内从16 Ω变化到8 Ω，因此输出电压电平通过该算法同步变化为48 V。变换器I1和I2分别对总负载电流贡献2.85 A和3.15 A。同样，当负载电阻从8 Ω变化到5.33 Ω时，本文算法将输出电压调节到47.4 V。变换器I1和变换器I2对负载电流的贡献分别为4.2 A和4.65 A。本文提出了一种通过仿真验证概念的方法，给出两个并联升压变换器性能的实验结果，该算法保证了负载均流与下垂法的负载调节特性一致，证明了该方法的有效性。

5 结束语

本研究给出了基于主电流控制的并联DC-DC升压变换器的改进方法实例，通过Matlab/Simulink仿真验证了基于主电流控制的改进下垂控制方法。该方法根据并联变换器的负载调节特性调整输出电压，保证了两个并联变换器的输出电压电平相同从而避免了直流母线上的循环电流。为了检验所提出的方法的性能，考虑了二种情况，即功率级不失配，失配10%，该算法保证了负载均流与下垂法的负载调节特性一致，证明了该方法的有效性。