一种非凸松弛化的多核集成回归方法*

倪成功 陆 扣 袁 旭 黄昌彬 徐兆瑞

（江苏大学计算机科学与通信工程学院 镇江 212013）

1 引言

支持向量机及其扩展的研究可以说是最成功的机器学习方法之一［1］。并且该算法已被广泛应用于各种应用领域。在支持向量机算法中，将数据映射到一个较高维的输入空间，然后在该空间中构造一个最佳的分离超平面。而避免在高维运算，则通过支持向量机的第二个重要应用—核函数。它使我们能够对高维非线性模型进行建模。在非线性问题中，可以使用核函数将原始数据映射到更高维空间，从而在所得的高维空间中使其成为线性可分问题（如图2 所示）。简而言之，核函数可以帮助更快地进行某些计算，否则就需要在高维空间进行计算。

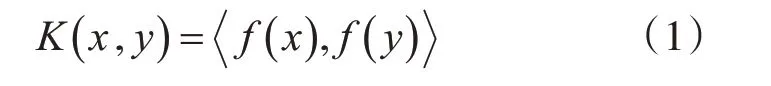
核函数定义如下：其中，K是核函数，x，y是N维输入。F函数将输入从N维映射到维空间。x，y是点积运算。利用核函数，我们可以计算高维空间中两个数据点之间的标量积，而不必显式地计算从输入空间到高维空间的映射。在很多情况下，计算核函数要比在高维空间中计算两个特征向量的内积容易。甚至简单内核的特征向量也可能维度上爆炸，对于如径向基核对应的特征向量是无限维的，但是，计算核函数却不会有这样的问题。

正是由于核函数的效果突出，不仅是对于回归还是分类都有很好的效果。我们将核函数应用到我们的算法中。为了增进核函数的效果，我们也结合集成学习。

集成学习［2］是提高性能的另一种方法，它在经验和理论上都比最佳单一回归器具有更好的回归性能。例如，Thongkam［3］等提出了一种结合Adaboost 和随机森林算法构建预测模型的方法。实验结果表明，该方法优于单一分类器和其他组合分类器。

根据上面的讨论，在集成学习的思想下，提出了一种新的基于核的回归方法，该方法是将多个弱回归器根据某种策略组合起来，构成一个单一的并且统一的回归函数。在集成学习中结合核函数的的最优点就是通过引入多个再生核希尔伯特空间，在每个希尔伯特空间中，核函数是独立的，不会受到其他空间的影响。这样可以完全保证所用的核函数的效果可以保持高效。同时为了能够选取出效果不错的核函数，我们采用的根据阈值选取核函数。通过根据一种通用基础模型预测出一个结果，在所有核函数池对每个核函数效果与基础模型的结果进行比较，挑选出比基础模型优秀的结果。这样我们再在这些相对优越的核函数中进行排序，我们挑选了前50核函数进行模型训练。

对于本论文，第二个重大创新就是，对于原本非凸模型，我们通过引入L1 范数和L2 范数，将模型进行解耦，从而可以实现对模型中的各参数进行求解。

综上所述，本论文的主要创新点如下：

1）我们将巧妙地将集成学习与核函数相结合。通过构造出多个再生希尔伯特空间，可以构造出互不干扰地核函数。

2）通过L1 范数和L2 范数结合，使用增广拉格朗日求解，这样使得原本非凸问题转变成可求解问题。

2 相关工作

2.1 支持向量机

支持向量机［4］是一种强大的分类器构建方法。它的目标是在两个类之间创建一个决策边界，以便能够从一个或多个特征向量预测标签。该决策边界（称为超平面）的定向方式应使其尽可能远离每个类的最近数据点。这些最近的点被叫做支持向量［5］。

给定标记的训练数据集：

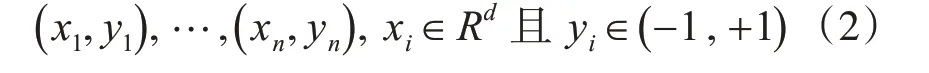
其中，xi是一个特征向量表示，yi是正负标签。

然后可以将最优超平面定义为

其中，w是权重向量，x 是输入的特征向量，b 是偏置。

对于训练集的所有元素，w和b将满足以下不等式：

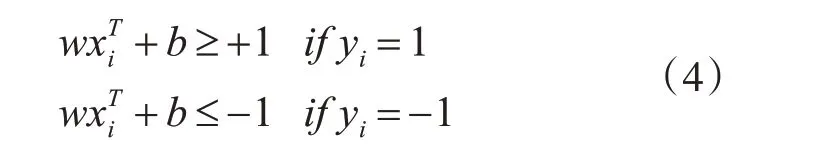
通过训练SVM 模型的目的就是找到w 和b，以使超平面分离数据并且最大化边界1 ‖w‖2。

将 |yi|(w+b)=1 的向量xi称为支持向量，如图1所示。

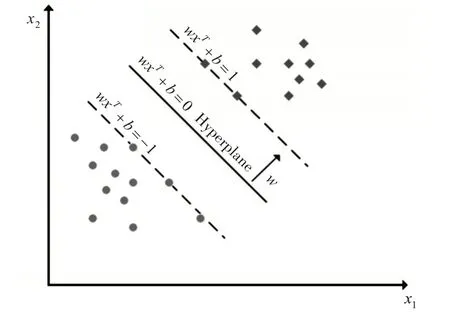
图1 线性SVM模型，分为两类（菱形和圆形）

支持向量机的另一种用途是核函数，它使我们能够对高维非线性模型进行建模。在非线性问题中，可以使用核函数将原始数据映射到更高维空间，从而在所得的高维空间中使其成为线性可分问题（如图2 所示）。简而言之，核函数［6］可以帮助更快地进行某些计算，否则就需要在高维空间进行计算。

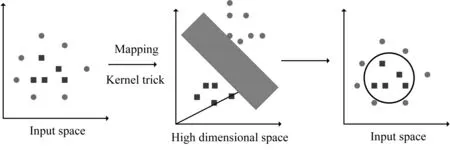
图2 核函数（不能通过线性SVM分离的数据却可以通过内核函数进行转换和分离）

核函数的选择是影响支持向量机模型性能的重要因素之一。但是，没有办法确定哪个核函数是对特定的模式识别问题最有效。选择最合适的核函数的唯一方法是通过试验。我们可以从一个简单的SVM 开始，然后尝试各种“标准”核函数。根据不同问题的特性，一个核函数可能要比其他核函数的效果更好。可以使用交叉验证以统计学上严格的方式从一组固定的核函数中选择最优核函数。

2.2 集成学习

集成学习是一种经典的机器学习算法，它综合了多个模型的输出进行预测。多个集成学习模型可以集成在一起，以提高对单个模型的准确性和鲁棒性。bagging 算法和boosting 算法都是集成学习中不同策略，它们的效果都要比单一分类器更精确、抗噪声能力更强而受到越来越多的关注。

布雷曼［7］在2001 年提出了一种非常独特的新分类器，称为随机森林（RF）。它是Bagging 算法的一种扩展算法，RF 可以在不删除变量的情况下处理数千个输入变量，并估计变量在分类中的重要性。

随机森林［8］是一个分类树的集合，其中每棵树贡献一个投票权，将最频繁的类分配给输入数据。RF 在每个节点的划分中使用输入特征或预测变量的随机子集，而不是使用最好的变量，这样可以减少泛化误差。此外，为了增加树的多样性，RF 使用bagging 或bootstrap 聚合来使树从不同的训练数据中得到子集。Bagging 是一种用于训练数据创建的技术，通过随机重新采样原始数据集并替换（没有删除从输入样本中选择的数据以生成下一个子集）。使用装袋法选择的使每个个体得到的每个子集都包含一定比例的训练数据集。训练子集中不存在的样本作为另一个子集的一部分被称为“袋外”（out-of-bag）。值得注意的是，通过引导过程，从未选择的元素中为集合的每个树形成一个不同的袋外子集。这些袋外元素不考虑用于树的训练，可以按树进行分类以评估性能。错误分类与袋外元素总数之间的比例有助于对可用于特征选择的泛化误差进行无偏估计。

3 多核集成回归

在这一节中，我们介绍了一种新的核集合回归方法，它可以帮助找到合适的核类型和基核回归中的参数。基核回归器通过在多个再生核希尔伯特空间（RKHSs）中构造不同的核函数，再根据我们制定的标准进行核函数的类型及其对应的参数。

3.1 再生核希尔伯特空间

再生核希尔伯特空间［10］是一种与核函数相关的特殊的希尔伯特空间，因为它（通过内积运算）重构该空间中的每个函数。它在机器学习中具有广泛的应用，例如SVR和径向基函数。

这些映射的集合可以通过包括所有可能的有限组合，邻近极限并根据所选核函数构造内积来扩展。

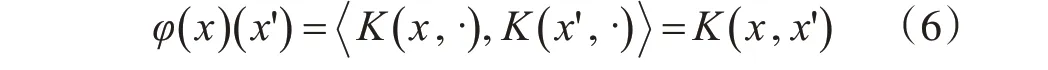
其中，K有K(xi，x)=K(x，xi)这样的对称属性。

接下来，列举下常用的核函数：

1）多项式核

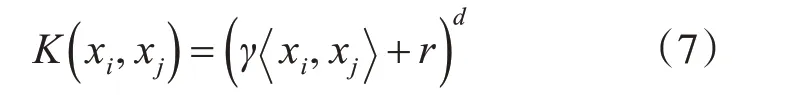
2）径向基核

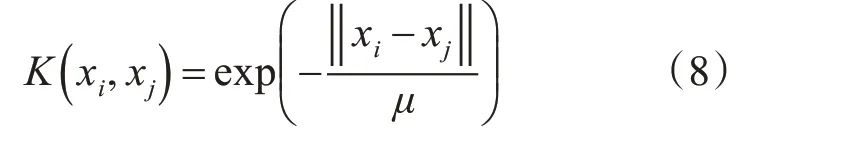
其中，a，b，c，μ∈ℜ。同时，K表示根据样本获得的Gram 矩阵。它是一个对称半正定矩阵，如下显示：

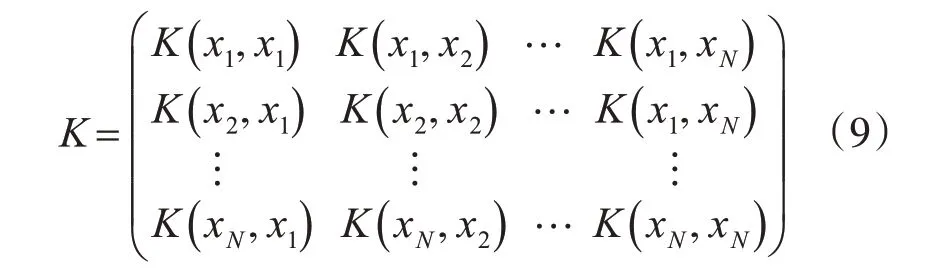
由此得到的RKHS具有HK中任何元素的每个求值算子和范数都有界的性质。对于Mercer 核：K:x×x→ℜ，函数x→ℜ 有一个与相应范数‖ ‖K相关的RKHSHK。标准框架通过最小化来估计未知功能：

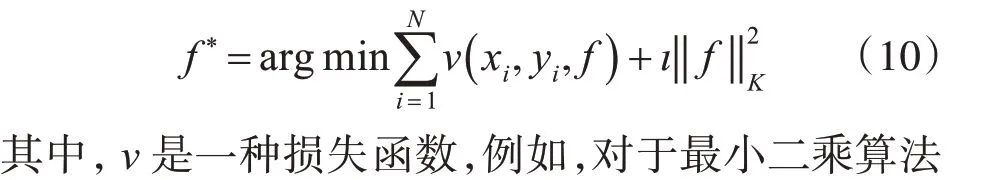
因此，该问题被简化为在有限维空间或系数αi上进行优化，这是支持向量机和其他核方法的算法基础。

3.2 最小二乘集成回归

在本小节中，我们介绍了我们提出的核集成方法。不同的核函数的种类及其参数用于构建基回归器。并提出了我们提出的核集合方法。

其中，前一部分‖Kα+b1-Y‖是平方损失，用作预测基核回归模型质量的标准。K是式（11）中所提到的Gram 矩阵。α是式（11）中的权重列向量，b是对于特定K的偏差项，1 是元素均为1 的列向量。Y是标签值。第二部分λαT Kα是平滑项，λ是控制第一项和第二项之间平衡的参数。

但是，不同的核函数的类型及其参数选择会导致不同的回归结果。为了获得更好的回归集成模型，在我们提出的核集成框架中结合了基核回归器。在以下部分中，对那些基本回归变量进行了优化和加权。

最小化目标函数，式（15）由两部分组成：第一个加号之前的是所有样本上回归量的总偏差，第二个是正则项，目的是限制回归系数的变化。引入惩罚参数以平衡它们。

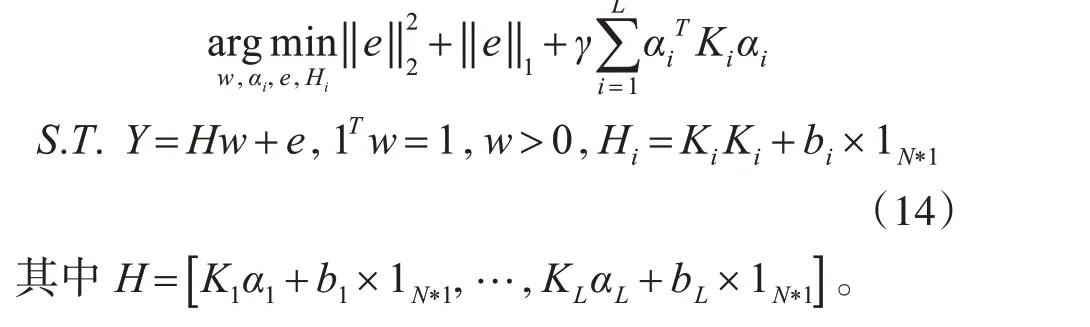
但是，由于式（15）是非凸问题，是无法求偏导来解决该问题，所以引入L1 范数和L2 范数，来将参数w解耦。解耦出的式（16）如下：由于式（16）中同时存在多个优化参数，因此采用增广拉格朗日乘数法［11］来解决它。首先，我们引入拉格朗日乘子μ，ξ，λ，η，τ，可以将这个约束问题转换为一个不受约束的问题，如下所示：

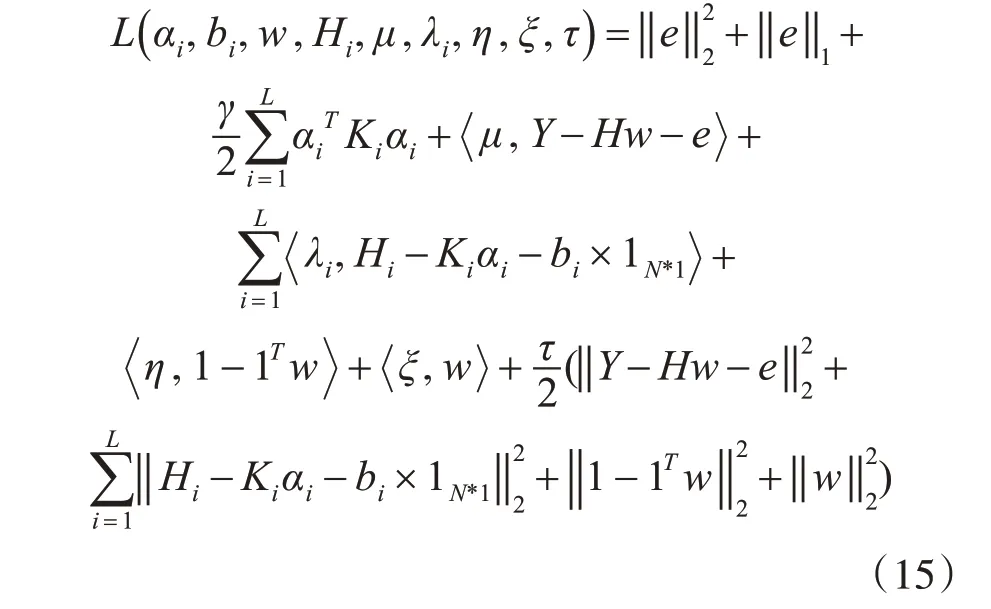
我们对式（17）中的αi，bi，w，Hi这些参数分别求偏导得到它们对应的更新式，如下所示：

1）对αi求偏导得：

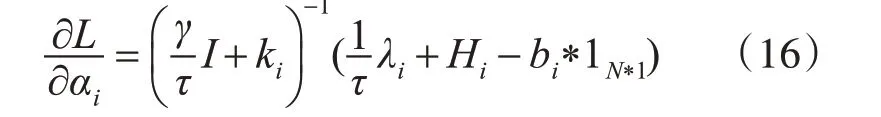
2）对bi求偏导得：

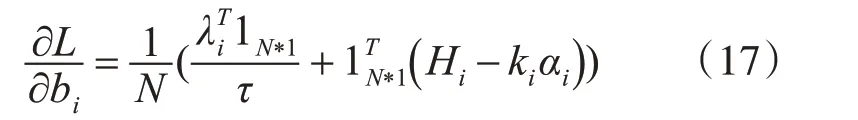
3）对w求偏导得：

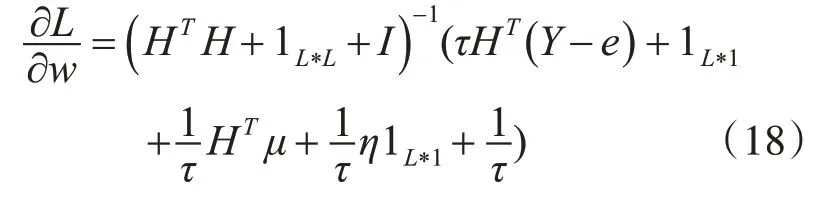
4）对Hi求偏导得：

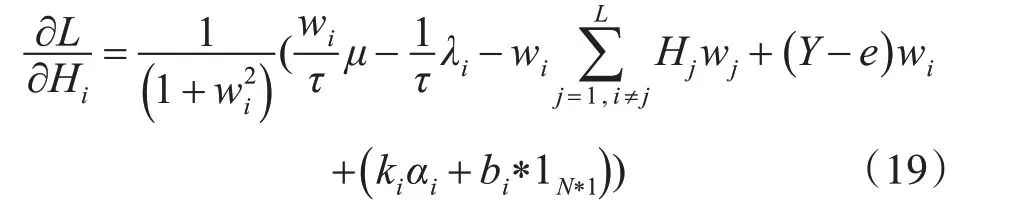
5）对于e求偏导得：

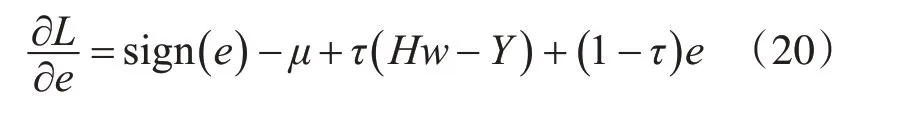
最后，我们需要采用梯度下降法依次去更新拉格朗日乘子，它们的更新式子如下：

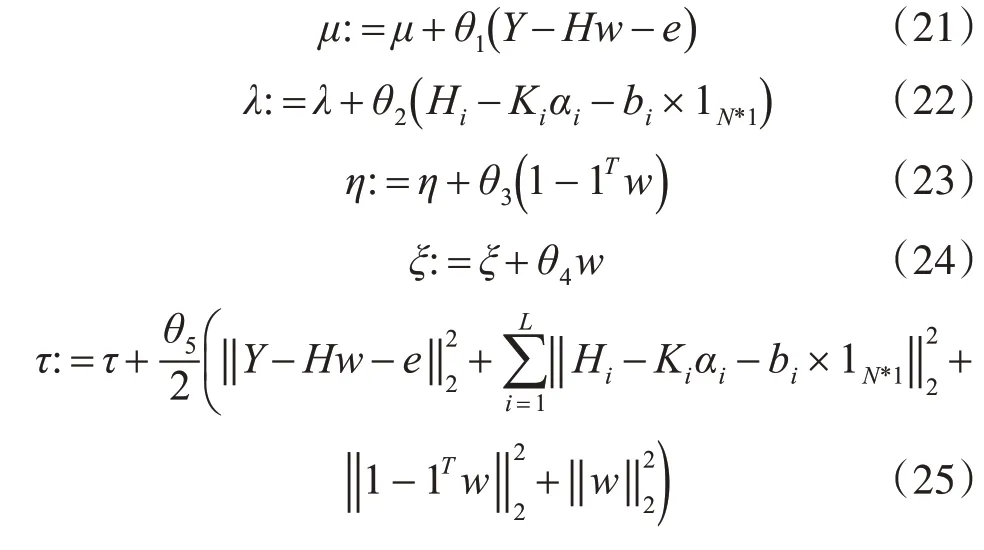
4 实验

在本节中，我们在公用回归数据集上测试多核集成模型。UCI 回归用于验证我们提出的方法的性能。

4.1 核函数参数设置

同多项式核函数选取方式一样，我们需要对一个参数(μ)进行选取，对参数(μ)的取值范围是：μ∈{1*1e-6，1*1e-5…1e3} 。这样构造出来的核函数，再按照多项式核函数的方法一样进行选取。对于其他类型的核函数及其对应的参数取值也一样的方法进行选取。通过此类方法的选取，我们可以得到多个多种类型的核函数及其对应的参数的取值，这样就形成了如同池子一样的核函数池，我们随机选取50个核函数，进行模型的训练。

而对于包括RF，XGBoost和Adaboost这三个集成方法，实验参数与叶节点的数量有关。为了实验公平起见，我们在我们的方法中设置叶节点的数量以匹配内核的数量。对于SAFER，我们对其self-KNN半监督回归器使用三个最近的邻居设置。

4.2 UCI数据集上回归实验

我们使用八个UCI 数据集测试了我们提出的模型在回归上的性能。 选择均方误差（MSE）和均方根绝对误差（MAE）作为评估标准［14］。

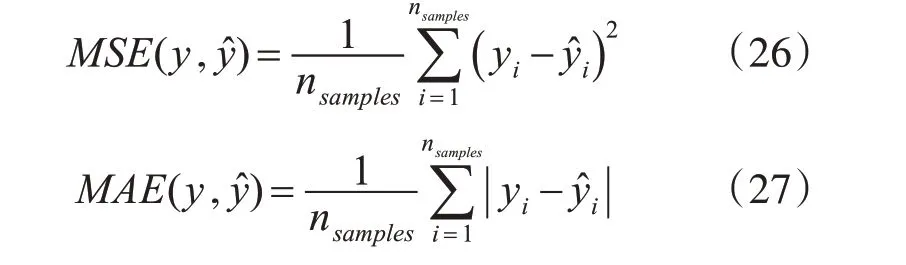
其中，nsample是测试集数据的个数。y^i是第i 个预测值，yi是测试集中标签。

我们在UCI 上使用八个回归数据集，包括Triazines，Mpg，Forest，Mg，RedWine，Space，Abalone 和WhiteWine。表1 列出了这些数据集的描述性信息。

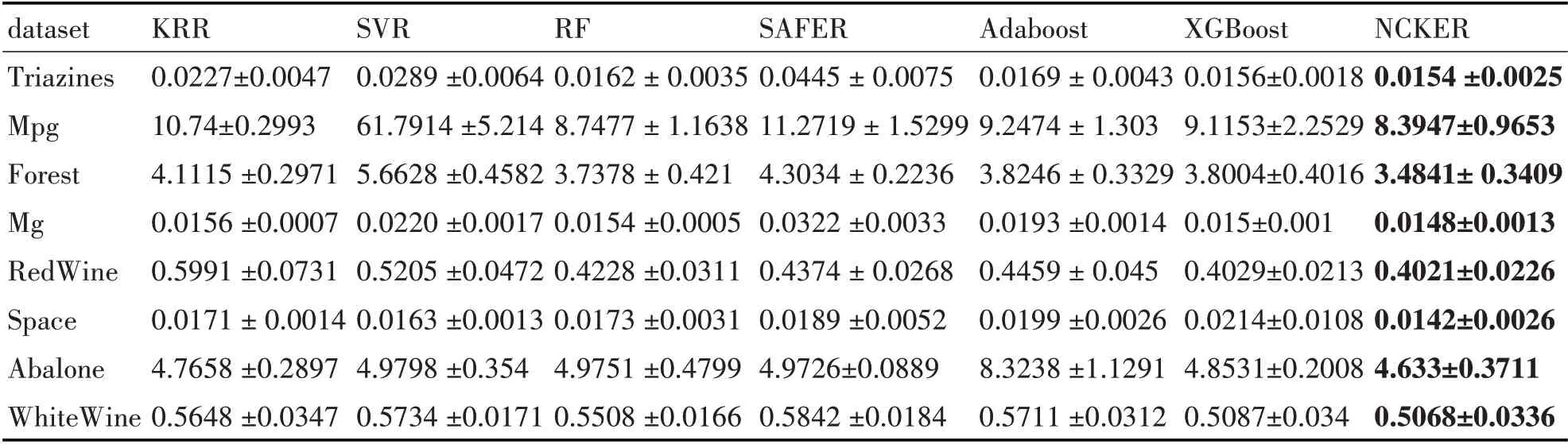
表1 测试集上MSE的平均与标准偏差

均方误差（MSE）是与均方误差或损失的期望值相对应的风险度量。根据表2 中的结果，我们提出的方法显示出强大的鲁棒性。

例如，在Space 数据集中，其中XGBoost 的回归效果最差，但我们的方法的回归性能最好，比第二最佳方法（SVR）高了0.0021。在RedWine 数据集中，SVR 方法获得的结果为0.5205，这使其成为最差的结果。与WhiteWine 数据集中第二好的方法（XGBoost）相比，比我们的方法低了3.7%。总而言之，我们提出的方法的结果具有比比较方法小的MSE。由于集成方法的优点，所提出的方法可以使用核方法来处理非线性数据集并获得更鲁棒的回归性能。

表2列出了MAE的结果，它是一种与绝对误差损失的预期值相对应的风险度量。从该表中，我们提出的方法在Abalone数据集中获得的最佳结果为1.5124，而XGBoost的结果为1.5412，略有落后。在Mg数据集中，我们的方法再次获得最佳性能，结果为0.0857。因此，从表2 的结果可以看出，我们的方法在所有数据集中均具有稳定且最佳的回归性能。证明了我们提出的方法利用了核方法和集成方法的结合优点。

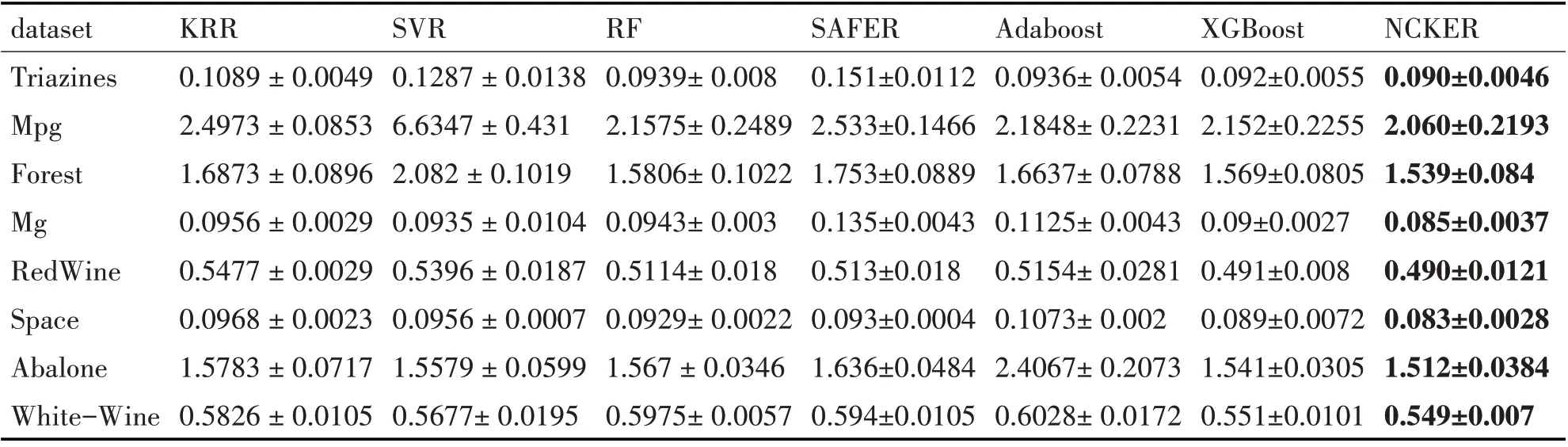
表2 测试集上MAE的平均与标准偏差

因此，可以得出结论，我们的方法可以找到合适的内核及其参数，这有助于提高回归性能。

5 结语

本文提出了一种创新的多核集合集成回归方法。我们的回归模型可以通过集成学习思想改进单一核回归方法，以在基本核回归器中找到合适的核类型及其参数。在算法中，从每个RKHS 空间并行优化基础核回归器并对其进行加权，以构建多核集成回归器。为了解决原始模型非凸问题，引入L1 和L2 范数，这样可以解耦参数，以达到可以求解。在UCI数据集上进行回归实验，足以证明我们的方法在保持其他同类比较回归方法（如随机森林，支持向量机和XGBoost）中的最低回归损失和最高分类精度方面的有效性。

将来，我们可以通过将目标函数更改为其他函数（例如折页损失函数）来研究我们提出的框架，以探索其在提议的集合框架中对数据集进行分类的适用性。此外，我们将把方法扩展到深度学习。