脉冲型地震作用下自由摇摆墩的反应特性研究

李 宁，王志强，李忠献

（1.天津大学建筑工程学院，天津 300350；2.滨海土木工程结构与安全教育部重点实验室（天津大学），天津 300350；3.中国地震局地震工程综合模拟与城乡抗震韧性重点实验室（天津大学），天津 300350）

引 言

自20世纪60年代Housner 首次提出“摇摆结构”以来［1］，摇摆响应便开始在抗震研究中广受关注。目前，对于摇摆响应的研究点在于它能够描述传统弹性摇摆体无法充分描述的系统［2］。一些摇摆结构响应的研究表明，摇摆可以用来解释砌体结构的运动［3-4］、说明无锚设备的地震特征［5-7］、解释地震易发区已屹立2500 多年的古希腊罗马神庙和中国庙宇的稳定性［8-11］。摇摆响应也为结构抗震减灾研究提供了思路。利用摇摆响应建成的建筑也数不胜数，如改造完成的Christchurch 机场一座33 m 高的烟囱［12］、改造完成的希腊Piraeus 三座30～38 m 高的烟囱以及最近建成的Wigram-Magdala 约束摇摆桥［13］等。

近年来对于墩的研究中，一些学者也将摇摆理论应用其中，摇摆隔震理论也得到了进一步探究。郭展等［14］提出一种基底摇摆隔震桥墩，通过设置底部加台以及高阻尼橡胶垫块实现摇摆隔震，发现其对于降低墩顶加速度和墩底剪力有显著作用。Cheng［15］试验研究了14 个含有预应力筋的钢筋混凝土块的自由摇摆情况，最终发现试件的振动频率和阻尼比均受到预应力筋直径的影响。何铭华等、郭佳等［16-18］基于性能的设计角度，对自复位单墩、双墩以及内置耗能钢筋和外置阻尼装置等桥墩形式均进行了摇摆墩抗震性能研究。

目前，对摇摆墩响应的研究仍缺乏振动台动力试验验证。另外，对于摇摆响应而言，一方面仍需要建立合理的摇摆理论模型［19］；另一方面需要通过某种方式来简化细长结构在地震激励下的设计过程，此时设计更关注墩顶摇摆最大反应。本文对自由摇摆墩运动方程进行分析，根据地震激励下自由摇摆墩顶部位移分析结果，提出基于“等侧移”原理的摇摆结构设计方法，为墩的设计提供参考。

1 自由摇摆墩经典摇摆方程推导

Housner［1］对细长刚体的研究指出，固定宽高比tanα、半对角线长度R和频率参数p的刚体，受到激励作用在刚性地基上绕O和O′点发生摇摆。研究中可近似假定自由摇摆墩为刚体，只考虑因碰撞而发生的能量损耗，不考虑结构本身的变形。

对于自由摇摆墩，其在摇摆过程中发生摇摆所需要满足的条件是>g·tanα，如图1所示。对墩的旋转点O和O′利用角动量守恒定理，有下式：

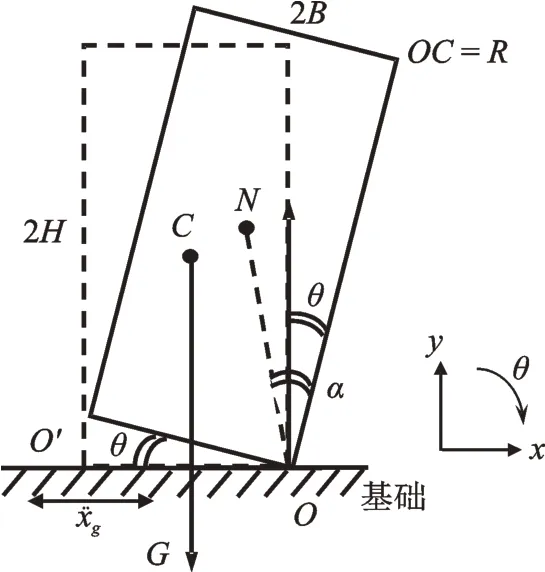
图1 自由摇摆墩柱的摇摆参数Fig.1 The rocking parameters of free rocking pier

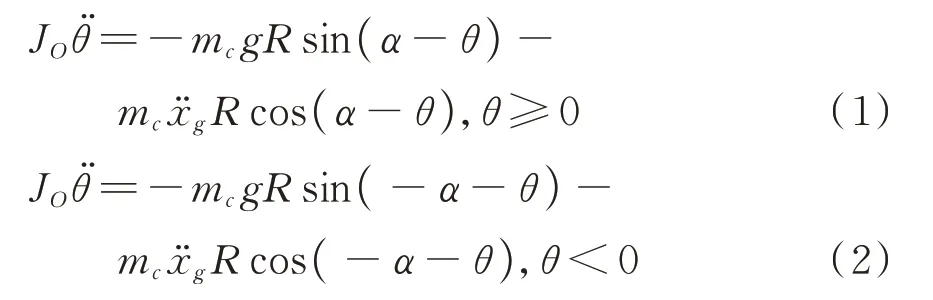
进而得到墩摇摆的经典控制方程：

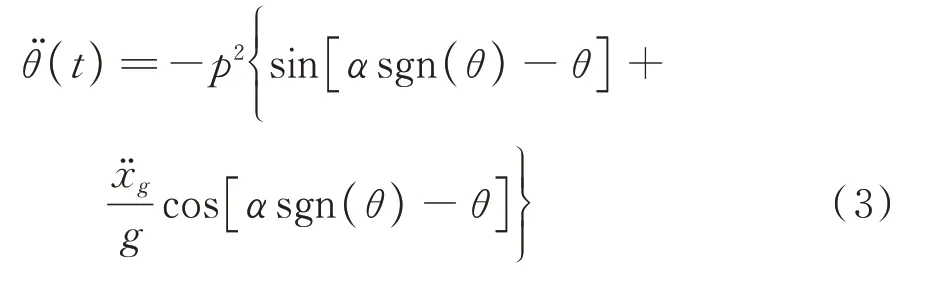
式中 频率参数p=几何量见图1所示，mc为墩质量，JO为绕O点转动惯量。在每次墩与地面碰撞过程中，碰撞前后角动量守恒，设碰撞前的摇摆角为θ1，碰撞后的摇摆角为θ2，则有：

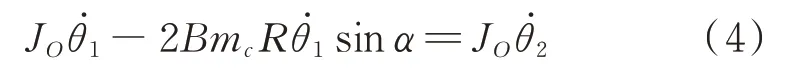
定义碰撞后的角速度与碰撞前的角速度比值的二次方为耗能系数cr，即：

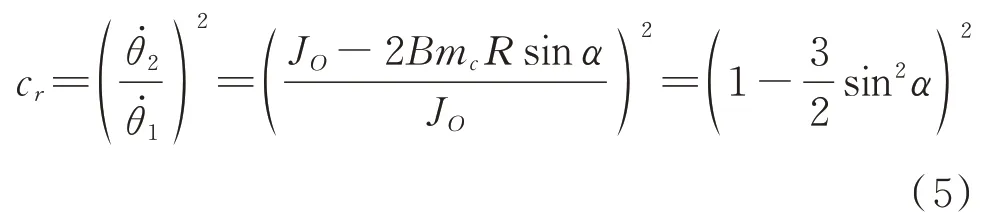
式（3）即为宽高比为tanα的墩在耗能系数为cr情况下的摇摆运动方程。摇摆运动过程中，冲击作用是非弹性的、耗能的。在墩摇摆的过程中，若摇摆界面相互作用损失了额外的部分能量，实际的耗能系数cr将小于由式（5）计算所得。接下来利用MATLAB［20］对式（3）进行分析。

2 基于不同激励作用的摇摆响应分析

基于式（3），考虑耗能系数式（5），有必要在研究地震激励作用前进行简单激励的分析，进而得到其对各个摇摆参数的响应情况。本节对不同激励作用进行了仿真分析。

2.1 单正弦激励

因单正弦激励与脉冲型地震动形式相近，地震反应研究也更关注该形式激励，故主要考虑墩在单正弦［21］激励下的响应情况。单正弦激励的脉冲段为：

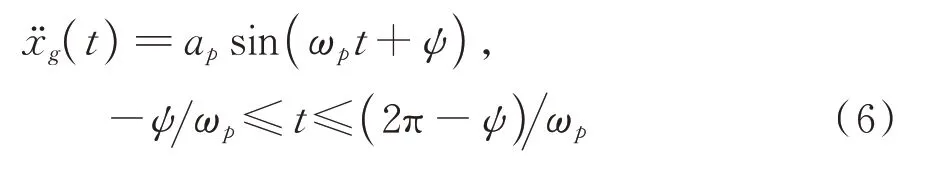
式中ψ=arcsin（αg/ap）为摇摆初始时刻相位角。

图2所示即在特定参数（p=2.14 rad/s，H=1.56 m，α=0.25 rad，ωp/p=5，cr=0.81）的单正弦激励下，不同脉冲幅值ap对应的墩的运动响应。

由图2可得，对于特定的单正弦激励作用。当ap=2.93αg时，墩经历了三次与地面的碰撞，但并未发生倾覆，此时因摇摆产生的墩顶部最大位移为0.731 m；当ap=2.94αg时，墩发生倾覆（θ>α），在这种情况下，墩与地面的碰撞发生于脉冲激励作用之后；当ap=6.77αg时，与前两种情况所不同的是，虽然墩摇摆角θ/α>1，但因惯性会使其重新实现复位，此处为了简化研究，后续研究中均假设当θ/α>1 时会发生倾覆。

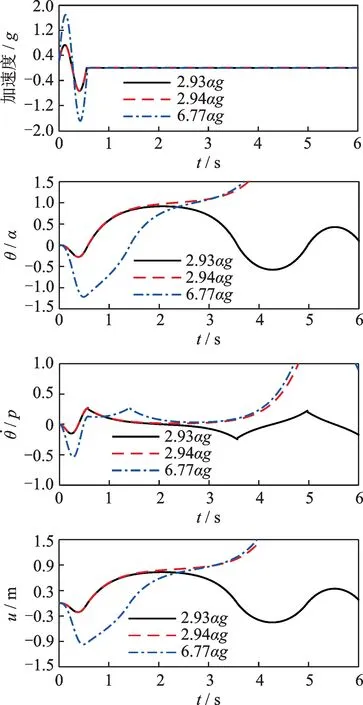
图2 不同幅值的单正弦激励作用下墩的摇摆响应Fig.2 The single sinusoid excites the rocking response of the pier under different amplitudes action

单正弦激励作用下，摇摆响应结果反映出墩的运动状态受到激励幅值和周期、宽高比等因素的影响。

2.2 正反Ricker 激励

Ricker 小波激励通常被用于脉冲地震激励模拟，包括正对称和反对称两种，分别被定义为高斯函数的二阶和三阶导数，其脉冲段表达式为：

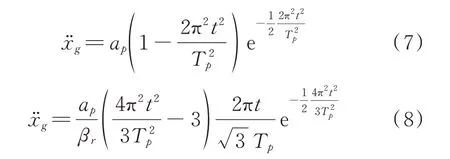
为保证峰值激励相等，取βr=1.3801。

2.2.1 特定参数Ricker 激励

图3所示即为施加特定参数（p=2.214 rad/s，α=0.1 rad，ωp=6.614 s−1，cr=0.9604）的正对称Ricker 激励，墩摇摆运动的情况。

由图3可得，当ap=0.311g时，墩在正对称Ricker 激励下的5 s 时间内与地面发生4 次碰撞，但并未发生倾覆，在摇摆过程中墩顶部位移达到了0.231 m；当ap=0.312g时，发生倾覆。

图3 正对称Ricker 激励下墩的摇摆响应Fig.3 Symmetric Ricker excites the rocking response of the pier

图4为同一墩施加特定幅值反对称Ricker 激励下的摇摆响应。当ap=0.35g时，墩在5 s 内受到了3次地面冲击，并且在碰撞过程中处于倾覆的边界（|θmax|=0.98α），在摇摆过程中墩顶部的最大位移达到了0.294 m；当ap=0.351g时，墩倾覆。

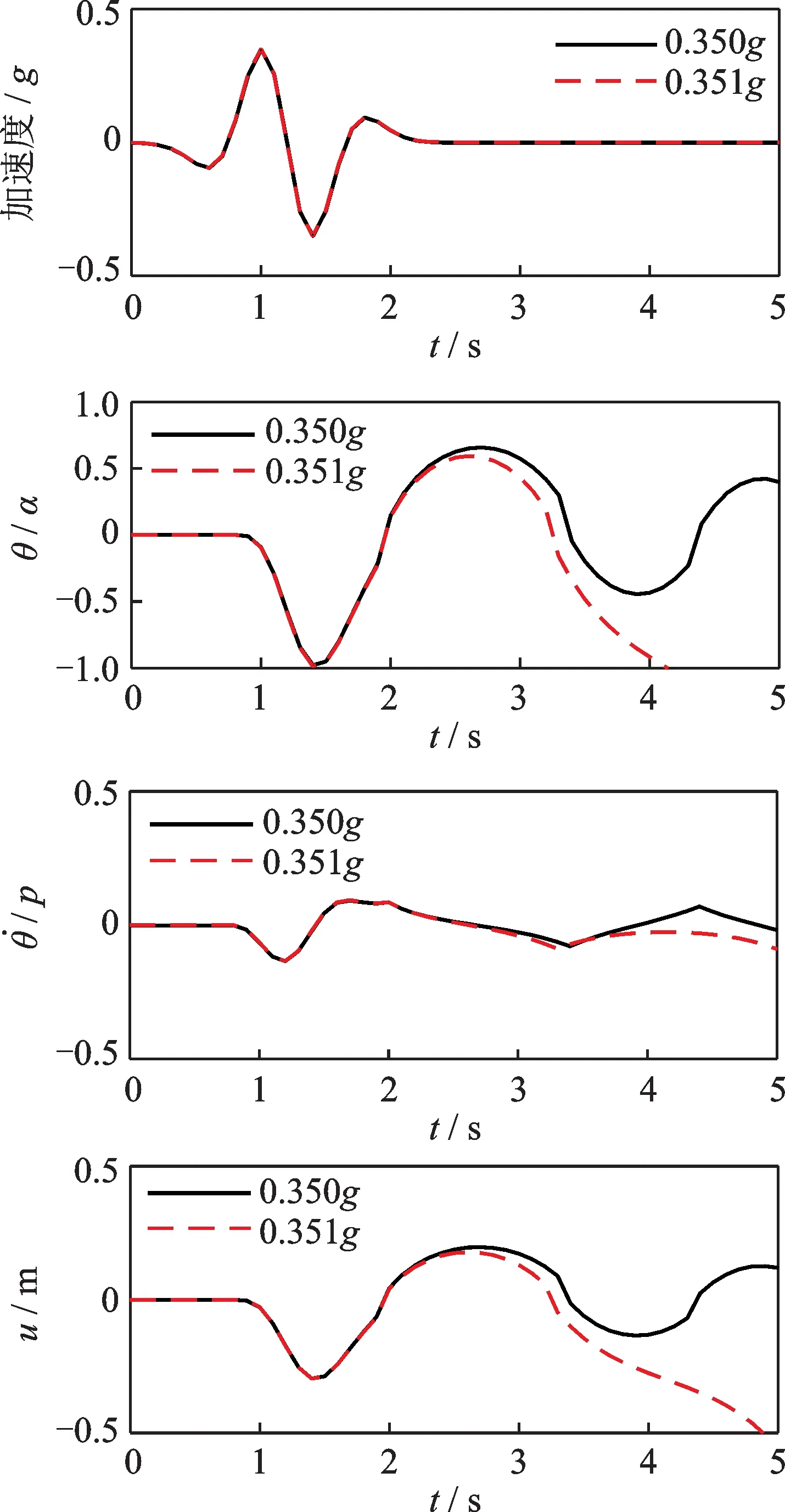
图4 反对称Ricker 激励下墩的摇摆响应Fig.4 Anti-symmetric Ricker excites the rocking response of the pier

对固定Ricker 激励作用，墩表现出倾覆状态，整体摇摆周期均较长。其倾覆状态与激励幅值ap对激励频率ωp均有较强的依赖性。

2.2.2 非特定Ricker 激励

上述分析不便于开展参数化研究，根据Π 定理［22］，Zhang 等［21］建议采用下式来简化式（3）：

式中ωp/p通常称为尺寸-频率参数，它取决于激励的频率和墩的尺寸；ap/（g·tanα）常称为无量纲加速度。此时，取α为定值（α=0.1 rad）可绘出正反Ricker 激励下最大反应θ关于参数ap/（g·tanα）和ωp/p的联合图谱，也称作摇摆谱，如图5所示。其中ap/（g·tanα）=［0～14］与ωp/p=［0～20］均为范围取值。在图5中，为简化考虑，假设当摇摆角最大值θmax>α=0.1 rad 时，墩倾覆。由图可得，ap/（g·tanα）和ωp/p对响应均有较大的影响。

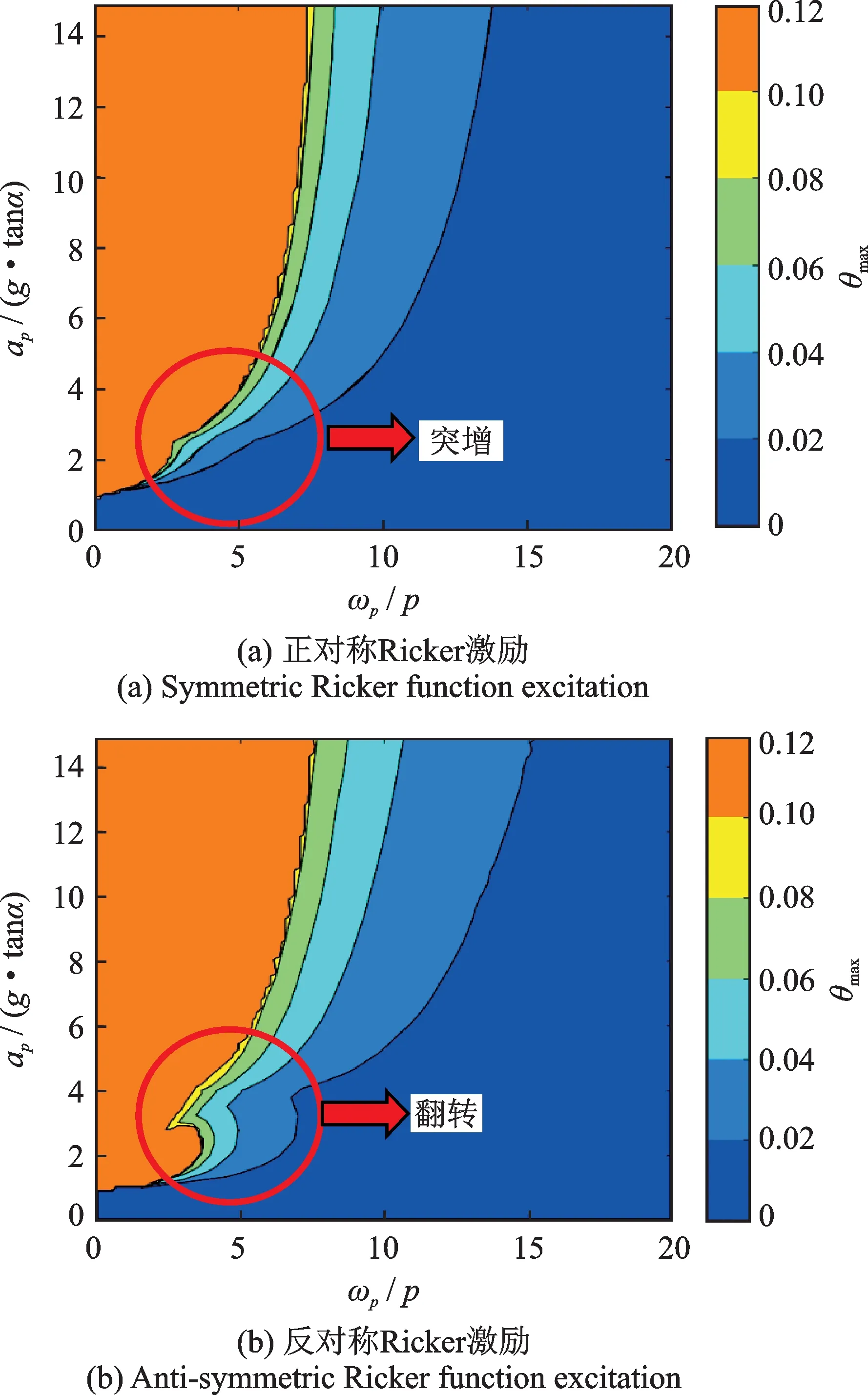
图5 基于非特定幅值的无量纲摇摆谱Fig.5 Dimensionless rocking spectrum based on unspecified amplitude

随着ωp/p的逐渐增大，ap/（g·tanα）整体也呈现逐渐增加趋势，但当ωp/p处于5 左右时，在正对称Ricker 激励作用下，摇摆谱有一个微小的突增；反对称Ricker 激励作用下，摇摆谱则有一个较大的翻转，这表明在摇摆初期，幅值ap增大时，可能会存在激励频率ωp较小的情况。总体而言，对于特定的ap/（g·tanα），ωp/p越大则摇摆角最大值θmax将越趋于减小。

对于正反非特定幅值Ricker 激励作用，自由摇摆墩表现出较强的倾覆状态，其倾覆状态与激励幅值ap、激励频率ωp和宽高比tanα均有较大联系。

3 自由摇摆墩的地震响应分析

地震激励下的摇摆响应分析对可采用摇摆功能设计的工程结构显得尤为重要。地震激励对自由摇摆墩的影响，应考虑不同类型地震动特性。本文分别考虑了近场脉冲型、近场无脉冲型和远场型三类地震动，并基于时程反应分析，对自由摇摆墩的反应规律进行探索。

3.1 某墩的摇摆响应分析

要保证墩在地震激励下可以发生摇摆，需满足PGA>g·tanα。对于一般的墩，α取为0.1～0.3 rad之间。

为研究地震激励下墩柱的摇摆情况，取某一实际自由摇摆墩，参数为α=0.214 rad 和R=3.58 m。根据周雨龙等［23］的研究，在选取地震动时，考虑到竖向地震激励下结构响应幅度很小，此处只考虑水平向地震作用。

式（3）显然受地震动PGA影响，在研究地震激励时，进行了PGA归准调幅。根据公路桥梁抗震设计细则［24］，此处水平向地震动PGA调整为0.408g（设防地震安全性评价结果取值）［23］，选取地震动记录如表1所示。

表1 不同类型地震动的选取Tab.1 Selection of different ground motion types

针对表1的地震记录，对其响应进行分析。

图6（a）为在远场型地震动作用下墩的摇摆响应，可知墩发生了较为剧烈的摇摆。在θ/α-t图中，墩所能达到的最大摇摆无量纲角度θ/α=0.325；相应在-t图中，墩所能达到的最大摇摆无量纲角速度=0.168；在u-t图中，墩顶部所能达到的最大位移u=491 mm（侧移比达7.02%）。并且，在整个摇摆过程中，共发生了26 次碰撞，9～20 s 内的碰撞最为激烈，而在前3～9 s 的摇摆角较小。

图6（b）为在近场脉冲型地震动作用下的摇摆响应。在θ/α-t图中，墩所能达到的最大摇摆无量纲角度θ/α=0.658，比远场增加102.5%；在-t图中，墩所能达到的最大摇摆无量纲角速度=0.229，比远场增加36.3%；在u-t图中，墩顶部所能达到的最大位移u=998 mm（侧移比达14.3%），比远场型增加103.3%。摇摆过程中墩与地面共发生16 次碰撞，在5～15 s 左右墩的摇摆较为剧烈。

图6（c）为在近场无脉冲型地震动作用下的摇摆响应。在θ/α-t图中，墩所能达到的最大摇摆无量纲角度为θ/α=0.086，比远场型减少73.6%，比近场脉冲型减少86.9%；相应的在-t图中，墩所能达到的最大摇摆无量纲角速度=0.089，比远场型减少47%，比近场脉冲型减少61.1%；在u-t图中，墩顶部所能达到的最大位移u=130 mm（侧移比为1.86%），比远场型减少73.5%，比近场脉冲型减少87.0%。摇摆过程中墩与地面共发生了30 次碰撞。

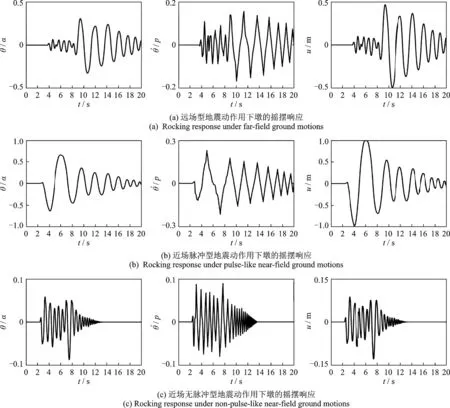
图6 三种类型地震动作用墩的摇摆响应Fig.6 The rocking response of the pier under three ground motion types

初步研究表明，近场脉冲型地震动的墩摇摆响应最剧烈，墩顶部会产生较大的顶端位移，摇摆角最大。因此，在考虑不同类型地震激励下自由摇摆墩初步设计时，基于变形的考虑，应对墩顶部位移反应规律进行分析。

3.2 自由摇摆墩顶部位移分析

考虑自由摇摆墩设计时的主要参数有：宽度B和宽高比tanα。对不同类型地震激励下顶部位移进行分析，确定出合理的墩设计尺寸。根据Manzo等［25］的研究，虽然式（3）中没有明确出现H，但实际中用H代替R作为尺寸参数更有意义。

在FEMA［26］地震数据库中，考虑近场脉冲型、近场无脉冲型和远场型三类，每种类型分别取两条地震动调幅并进行分析。所选取的地震动如表2所示。

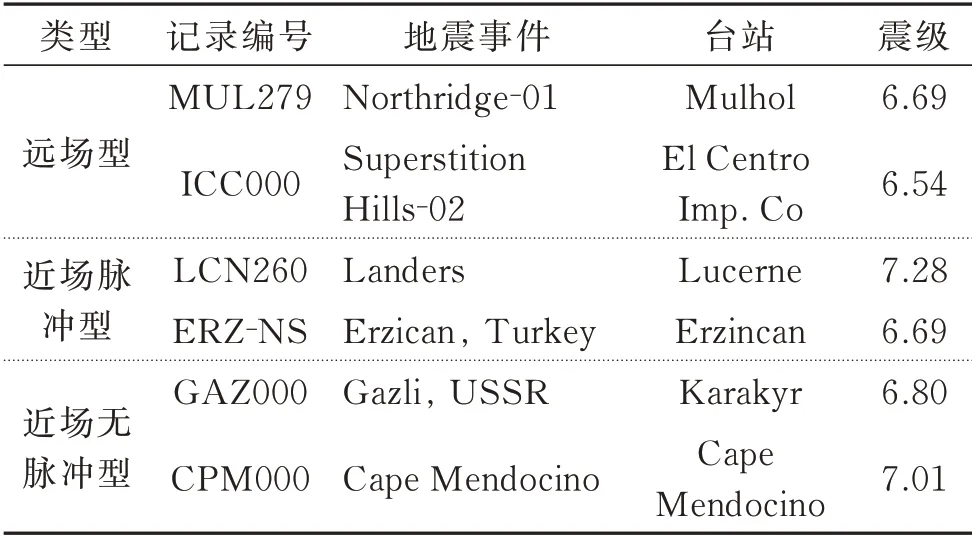
表2 分析位移时不同类型地震动的选取Tab.2 The selection of different ground motion types in the displacement analyses

图7所示为不同高度H下墩顶部的位移响应（PGA=0.408g），其中H=500 m 是为了近似分析2H→∞时的位移响应。可以得出，对于不同类型的地震动，所有宽高比相同、但高度不同的自由摇摆墩，只要不接近倾覆，顶部位移（umax，单位：m）基本相同。同样的结果适用于所有测试过的地震动。其中各条线的五角星标志各地震动激励下发生摇摆倾覆。

图7 不同高度下墩顶部位移与α 的关系Fig.7 The relation between the pier top displacement and α at different heights

由于地震动的不确定性，有必要通过多组激励比较的统计数据（例如：取各组每一条水平向地震动结果的平均值）来说明问题。本节中，从FEMA［26］数据库中三类型地震动中各选取14 条地震动，绘制不同类型自由摇摆墩的平均谱，如图8所示。

由图8可知：

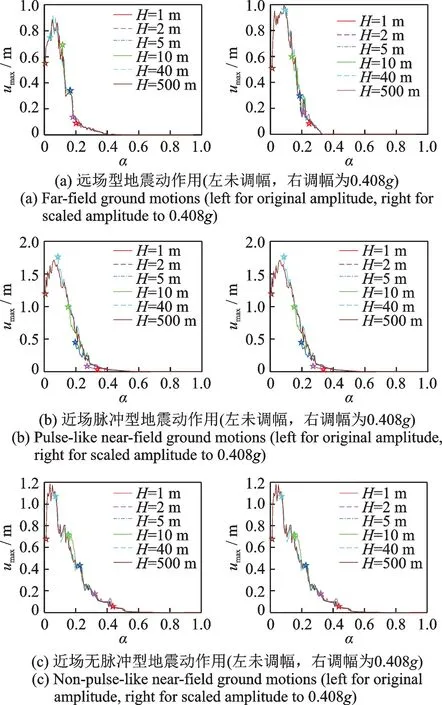
图8 不同类型地震动情况下自由摇摆墩柱平均谱Fig.8 The average spectrum of free rocking pier under different ground motion types

（1）通过对多条地震摇摆谱的统计处理得到的平均弹性谱比单条地震弹性谱更光滑。

（2）调幅后自由摇摆墩平均谱的umax（单位：m）与调幅前有较大差异，表明PGA对平均谱有较大影响。

（3）只要墩不接近倾覆，自由摇摆墩顶部位移就与其尺寸弱相关。此时，无需为每个墩尺寸计算不同的频谱，而是可以计算2H的平均谱或设计谱（建议取2H=1000 m 计算），并用它来确定墩顶部的位移需求；此规律也可理解为“等侧移”规律。

（4）随着墩接近倾覆，“等侧移”规律不再适用：较小尺寸的比较大尺寸的墩具有更大的顶部侧移比；此外，随着墩的倾覆，谱线斜率急剧增加，即α的小幅下降即导致墩顶位移大幅增加。这种趋势表明，对墩进行合理设计需避开频谱的陡峭部分，因为此时设计中略强的地震都会引起顶部位移极大增加。也可以认为，“等侧移”规律适用于设计摇摆区域（非临近倾覆区段）。

（5）上述三类地震动摇摆谱呈现出一些相近的规律：

i.随着α增加，墩顶位移会达到一个峰值，约为α=0 左右的1.5～2.0 倍，而后下降；

ii.α的进一步增加导致自由摇摆墩顶部位移的单调减小；

iii.因为α达到PGA/g时自由摇摆墩不发生摇摆，顶部相对位移为零。

4 基于“等侧移”摇摆谱的自由摇摆墩设计方法

由前述分析可知，自由摇摆墩只要未发生倾覆，二维形式的摇摆位移谱与自由摇摆墩尺寸关联性不大。在进行设计前，可以使用“等侧移”规律进行初步估算。

本文建议的具体设计步骤如下：

（1）在二维形式摇摆位移谱umax-α图中绘制容差线：uc=2Htanα=2Hα；

（2）根据设计场地类型、抗震设防烈度等确定需要调整的地震动PGA值；

（3）绘制出不同类型地震动下，自由摇摆墩的2H→∞（2H=1000 m）时的频谱，此频谱与容差线uc相交点所对应的α轴坐标即为αk；

（4）本文使用容量值2.0 来确定所设计自由摇摆墩的α，即：αD=2.0αk。容量系数2.0 是为将设计点从频谱的陡峭部分移开，更确切的数值应通过更细致的统计分析得出，但不影响本文设计方法的提出，它用于保证自由摇摆墩稳定不倾覆。

取一实际工程应用的某公路大桥［27］参数进行验证，摇摆墩设计高度为2H=6.8 m，2R=6.9 m，实际宽高比为0.210。根据Makris 等［28］的建议，设计时可假定其摇摆响应相当于2H=10 m 的墩的摇摆响应。地震激励下的设计如图9所示。最终不同类型地震激励下自由摇摆墩设计位移及宽高比如表3所示。

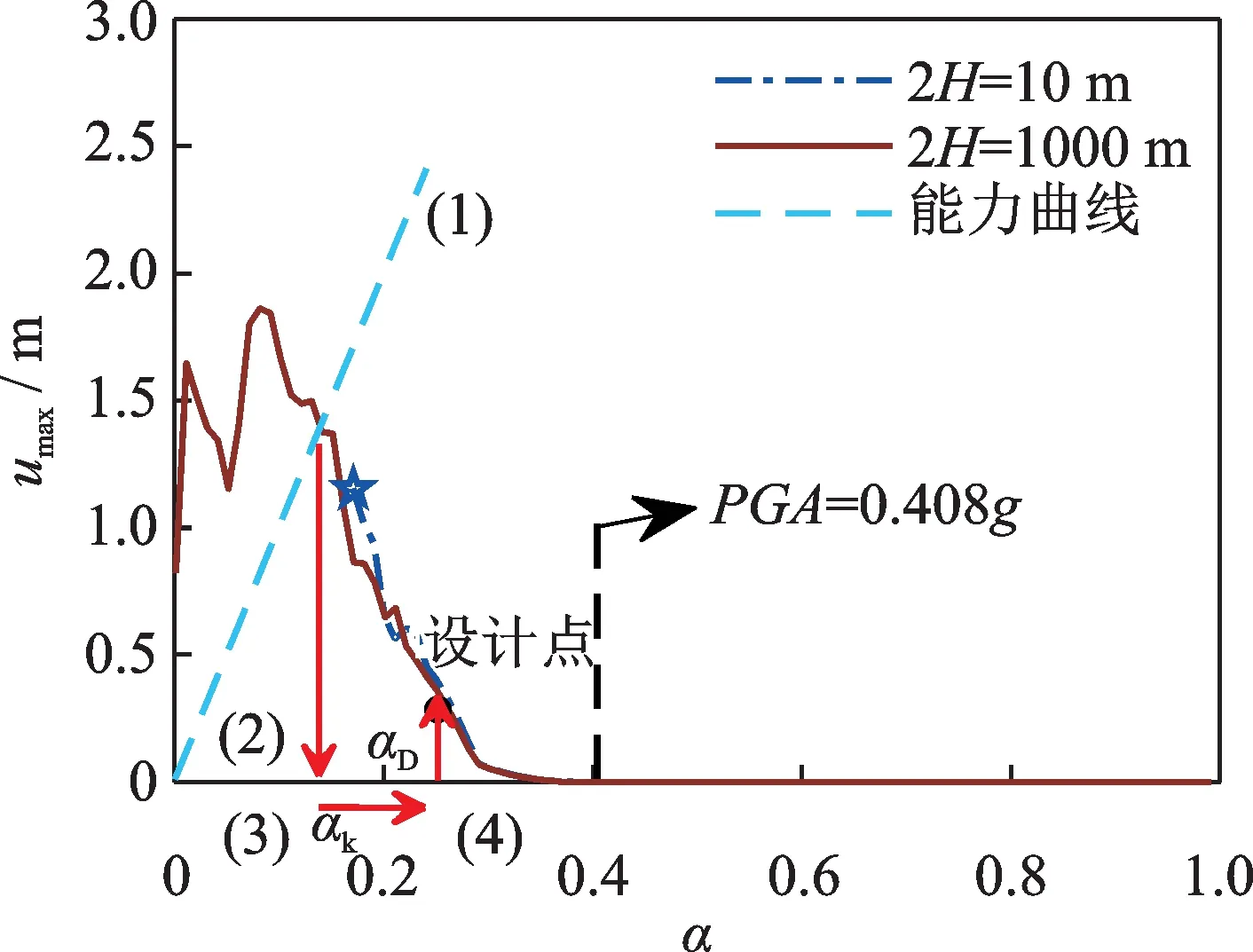
图9 基于摇摆谱单墩设计流程图Fig.9 Design of pier based on rocking response spectrum

由表3可知，不同类型地震激励下，设计宽高比仍有较大差异，但为前期响应试算提供了参考价值。该墩的平均设计αD=0.248，与实际宽高误差为18.10%，实际设计是更保守的；同时也发现，三种类型地震动作用下，2H=1000 m 时墩顶部的设计位移值与2H=10 m 时差值较小，平均差值为7.51%，这也初步证明了“等侧移”规律设计方法的适用性。

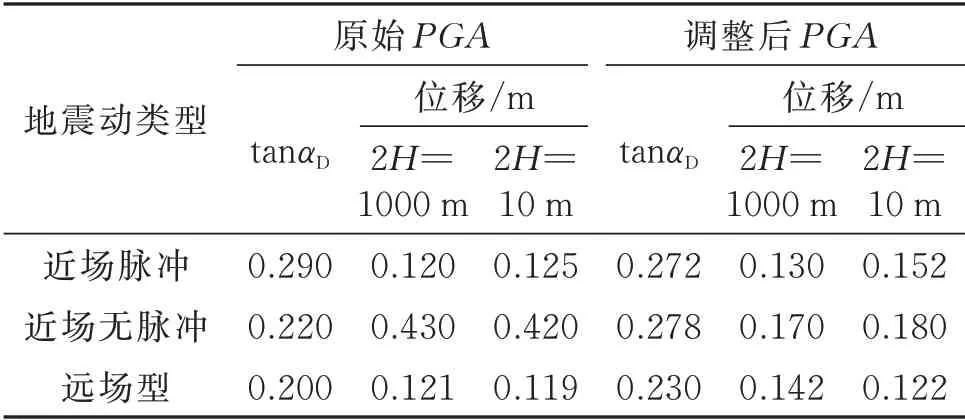
表3 不同类型地震激励下自由摇摆墩的设计位移（考虑容量系数为2.0）Tab.3 Design displacements of free rocking piers for dif⁃ferent ground motion types（capacity factor is 2.0）

5 结 论

本文通过对不同脉冲激励下自由摇摆墩响应分析和最大反应的规律研究，主要得到如下结论：

（1）单正弦激励幅值ap增大时，墩易倾覆；正反Ricker 激励作用下，随着ωp/p逐渐增大，ap/（g·tanα）整体也逐渐增大，反对称Ricker 激励作用下，摇摆谱出现一个较大角度的翻转，表明在摇摆初期，幅值ap增大时，可能会存在激励频率ωp较小的情况；对于固定ap/（g·tanα），ωp/p越大则摇摆角将越小。

（2）对多组不同类型地震激励下自由摇摆墩顶部位移分析得到“等侧移”规律，即：所有宽高比相同、但高度H不同的墩，只要不接近倾覆，其顶部位移就不取决于其尺寸；对这部分频谱，可直接计算2H=1000 m 时的设计频谱，并可计算任意自由摇摆墩顶部的位移需求。

（3）提出基于“等侧移”规律自由摇摆墩的设计方法。当2H=1000 m 时墩顶部的设计位移值与2H=10 m 时差值较小，平均差值为7.51%，证明了“等侧移”规律设计方法的适用性。

需要说明的是本文仅探讨了简化型体（细长型、未考虑复杂上部结构）、发生弹性碰撞摇摆的墩在多种脉冲载荷下的一般反应规律，更复杂的阻尼效应、碰撞耗能拟将在后续研究中开展。