横波钢板剪力墙内嵌板与边框柱相互作用研究

王 威，王冰洁，罗麒锐，徐善文，孙壮壮，李鹏洛

（西安建筑科技大学土木工程学院，陕西 西安 710055）

引 言

非加劲平钢板剪力墙具有较高的延性和抗侧承载力，但易出现面外屈曲变形，整体稳定性较差［1-3］。波形钢板面外刚度较大，可有效提高剪力墙的面外稳定性［4-5］。当波纹板为水平布置时，因手风琴效应使竖向荷载几乎全由边框柱承担，横波钢板水平抗剪承载力得以有效发挥。

钢板剪力墙是双重抗侧力结构，边缘框架的强度和刚度是保证钢板充分发挥力学性能的基础，同时钢板对框架也有一定影响，两者之间的相互作用与整体力学性能有密切联系［6］。因此，研究板框相互作用并深入了解其受力机理，有助于控制构件的屈服顺序和优化其截面几何设计，最大程度地发挥整体力学性能。

国内外学者对板框相互作用开展了研究。王萌等［7］通过对带连梁低屈服点钢板剪力墙力学性能的研究，得出内嵌钢板与边缘框架的相互作用能有效提高整体结构承载力、承载效率及耗能能力。Habashi 等［8］通过研究板与框架的剪力分担率，发现板在加载初期承担大部分剪力，但当板的对角线屈服区域开始扩展后，其利用率逐步下降；当屈服区域扩展到整个板时，框架承担大部分侧向荷载。Machaly等［9］通过数值模拟研究平钢板剪力墙的极限抗剪强度，结果表明当框架的抗弯刚度不足时，板不能充分达到其屈服强度。Sabouri-Ghomi 等［10］针对平钢板提出了PFI（Plate-Frame-Interaction）模型，将板和框架分开考虑来说明板框相互作用。Zirakian 等［11］考虑到平钢板可能同时有剪切变形和弯曲变形，提出了考虑弯剪耦合变形的PFI 模型以更好适应不同的受力情况。

考虑到横波钢板与平钢板的受力机理有所区别，适用于平钢板的PFI 模型可能不能直接适用于横波钢板，需要改进某些计算参数以适应横波钢板的参数变化［12-13］。然而，目前对于几何参数变化对板框相互作用影响的研究还较少。因此，本文以横波钢板剪力墙为研究对象，通过ABAQUS 有限元软件建立关于高宽比、板厚及开洞的变参模型，分析其板框相互作用影响参数及剪力、耗能分配规律，并采用基于弹塑性变形分析的改进PFI 模型来预测其受力全过程。

1 有限元模型与试验验证

选取本课题组之前的试验来验证有限元模拟横波钢板剪力墙破坏形态与滞回性能的准确性及合理性［14-15］。

1.1 试验简介

参照试件选用本课题组设计的缩尺比例为1∶2的单层单跨横波钢板剪力墙，试验在西安建筑科技大学结构与抗震实验室进行。加载前在试件顶梁中部由液压千斤顶施加竖向荷载150 kN，之后采用低周往复水平加载制度，由荷载和位移混合控制，屈服前采用荷载控制，屈服后采用位移控制。当试件破坏或荷载下降至峰值荷载的85%时，停止加载。试件最终因边框柱面外变形过大而发生失稳破坏。

1.2 有限元模型

采用ABAQUS 有限元软件建立单层单跨横波钢板剪力墙模型，建模方法可参考本课题组已发表的相关论文［16］。钢材本构选用弹塑性强化模型，弹性模量E=210 GPa，强化阶段模量为0.01E，泊松比μ=0.3，屈服强度可根据材性试验结果得出。其本构表达式如下所示：

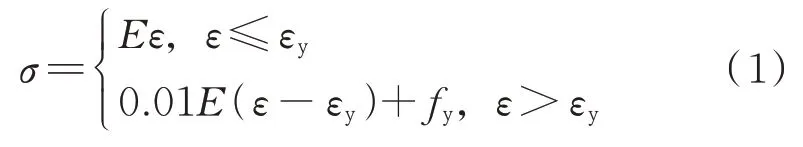
式中σ为应力；ε为应变；εy为屈服应变；fy为屈服强度，取235 MPa。

边缘框架、内嵌板与加劲肋均采用Solid 实体单元建模，网格采用C3D8R 六面体线性减缩积分单元，并采用结构化网格划分方式。为满足精度要求及提高计算效率，经试算后确定网格最小尺寸为30 mm。

模型加载原理与试验相同，顶梁中部设置有加载点，第一分析步设置竖向荷载150 kN，在加载过程中保持荷载不变；第二分析步采用位移控制加载，将屈服前的力控制阶段转化为同等条件下的位移控制阶段，且屈服后的位移控制阶段与试验相同。转化原理是屈服前试件刚度基本不变，力可在同等条件下等比例转化为相应位移。

各构件之间连接均采用Tie 约束来模拟真实焊接。不考虑梁轴向变形的影响，顶梁和底梁均绑定为刚体。底梁中部耦合点约束所有自由度来模拟固接，边框柱中部设置有面外约束。验证模型如图1所示。

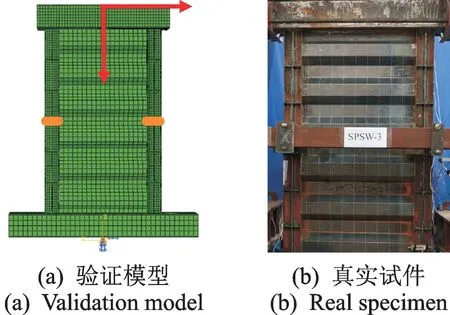
图1 验证模型示意图Fig.1 Schematic diagram of validation model

1.3 试验验证

1.3.1 破坏形态

验证模型与真实试件的破坏形态对比如图2所示。由图可知，最终破坏都是由边框柱面外屈曲引起的整体失稳破坏，受力主要集中于柱上，板未充分发挥力学性能。该对比图可说明有限元方法可较为准确地模拟试件受力形态。

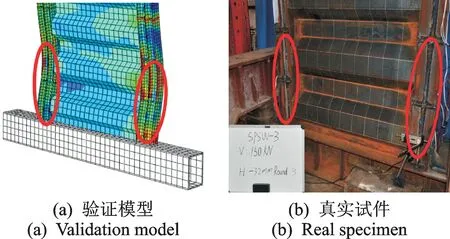
图2 破坏形态对比Fig.2 Comparison of failure modes

1.3.2 滞回性能

试验和有限元验证的滞回曲线对比如图3所示，试验的峰值荷载为383.15 kN，有限元模型的峰值荷载为405.16 kN，误差为5.4%。模拟曲线与试验曲线吻合度较高，但有限元模型忽略了材料的初始缺陷和加工误差等因素的影响，且上下梁都为理想刚体，因此模拟的滞回曲线更加饱满、极限承载力更高、延性更好。该对比图可证实此数值模拟方法适用性较好。

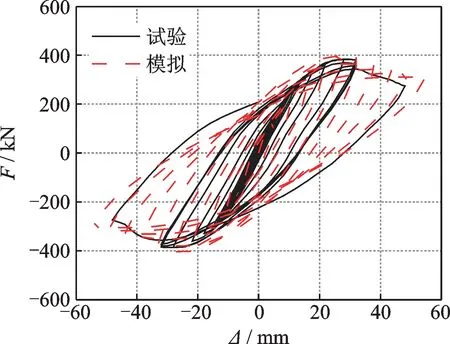
图3 滞回曲线对比Fig.3 Comparison of hysteresis curves

2 横波钢板剪力墙参数设计

2.1 边框柱变参对比

由破坏形态可知，H 型钢柱的刚度太小，未能提供足够的面外约束，先于板发生屈服，板未完全发挥作用，板框相互作用效果较差，匹配不合理［16］。为增大柱的刚度，以1.2 节的验证模型为基础，提出两种解决方案：第一种是增大H 型钢柱翼缘宽度；第二种是将H 型钢柱更换为方钢管柱。

为更好地比较增大H 型钢柱翼缘宽度与更换为方钢管柱之间的差别，将H 型钢柱翼缘宽度由75 mm 增大至150 mm，方钢管截面边长为150 mm，管壁厚9 mm，其余参数均相同，如表1所示。

表1 边框柱变参模型Tab.1 Variable parameter models of frame column

变参模型的骨架曲线对比如图4所示。由图可知，与增大H 型钢柱翼缘宽度相比，方钢管柱模型的极限承载力和初始刚度都更大。由最终变形图可知，H 型钢柱模型依然有面外屈曲变形，应力主要集中于柱上，板利用率不高；方钢管柱模型无屈曲变形，应力主要集中于板上，整体力学性能发挥更充分。

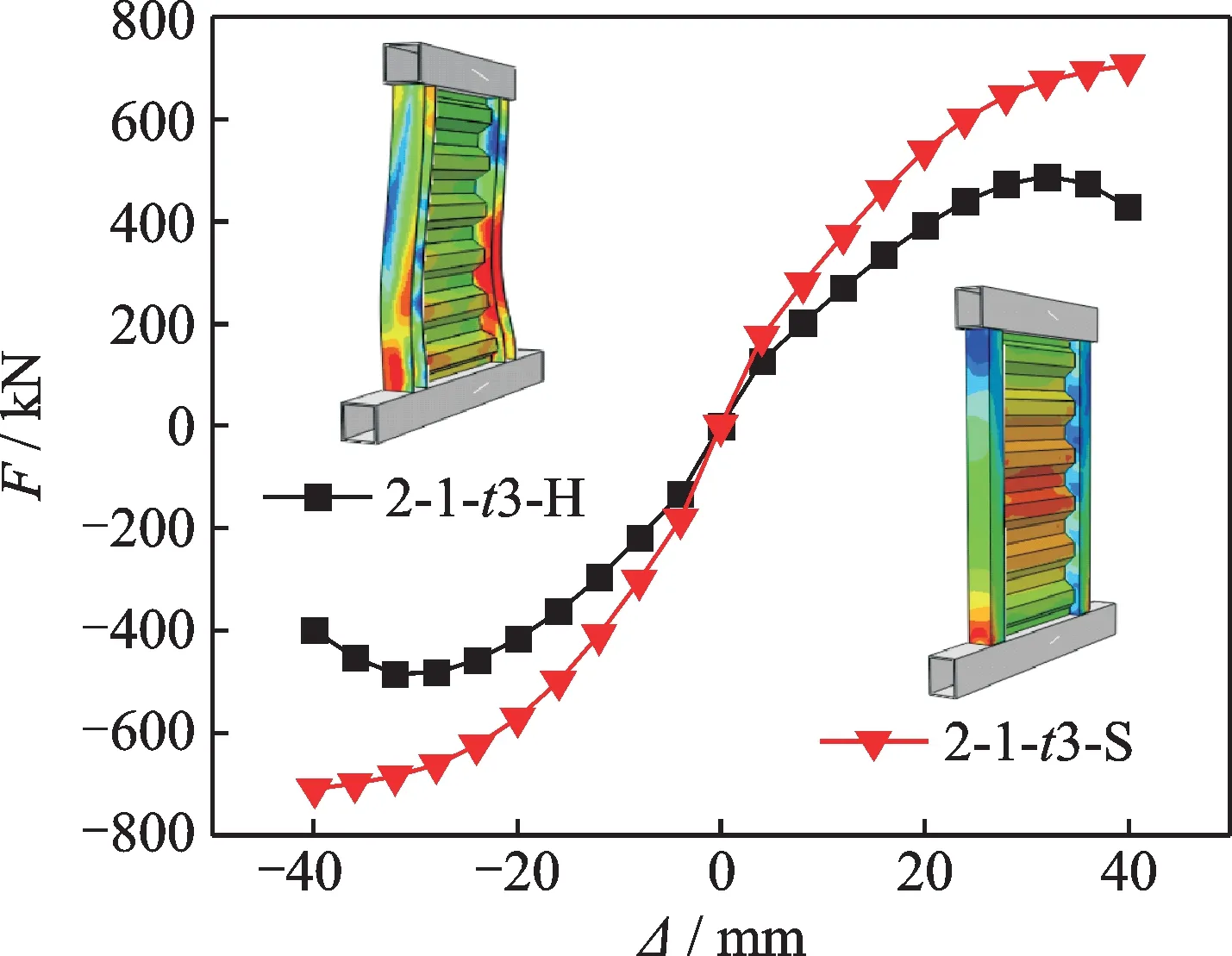
图4 骨架曲线对比Fig.4 Comparison of skeleton curves

2.2 板变参模型

方钢管柱与板的相互作用效果较好，匹配度更合适。因此，基于1.2 节的验证模型的建模方式及结果，边框柱的形式由H 型钢变为方钢管，板变参形式有高宽比、厚度及开洞，其余建模参数均相同。本文建立了23 个变参模型来研究板框相互作用，具体参数如表2所示。

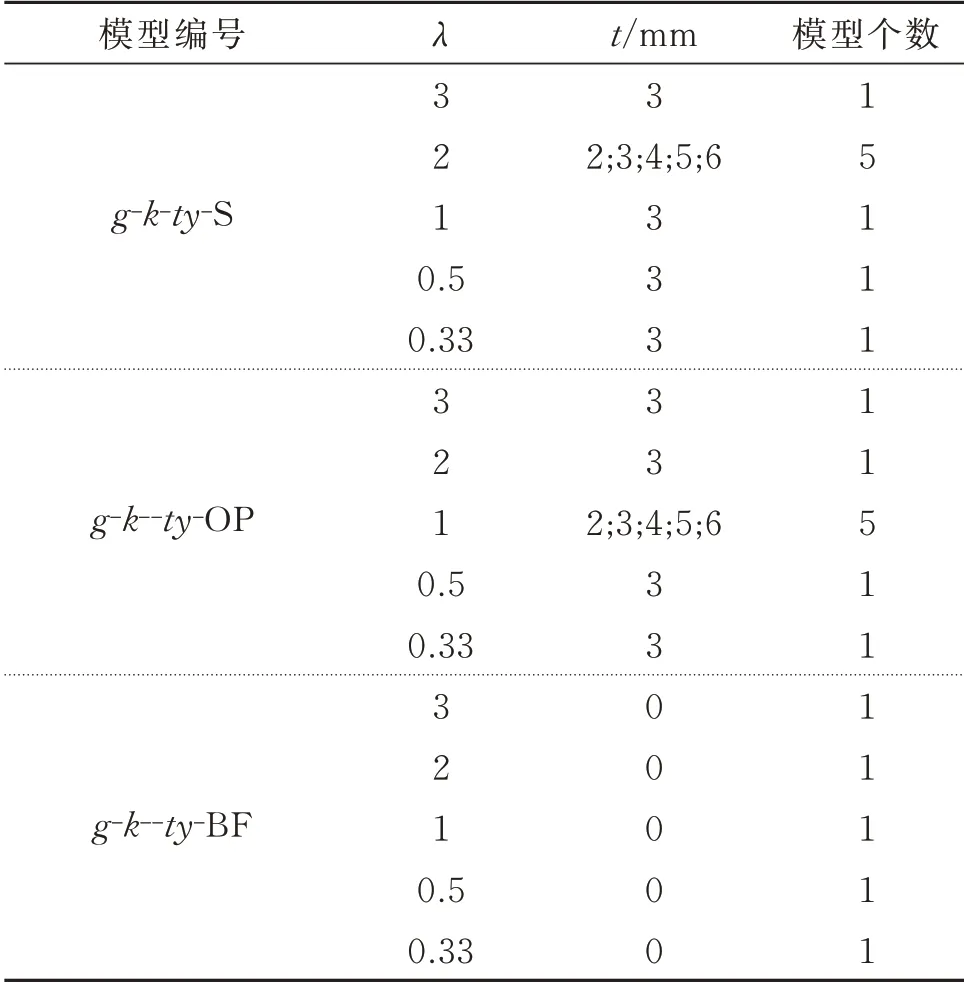
表2 板变参模型Tab.2 Variable parameter models of plate

为更好地观察剪力墙整体变形效果，变参模型未设置边框柱加劲肋及面外约束。高宽比的改变为控制板高为1980 mm，只改变宽度。加载最大层间位移角取规范限值1/50。板开洞形式为矩形，宽度与高度均为对应板长的1/3，如图5所示。

图5 板开洞示意图Fig.5 Schematic diagram of plate with opening

3 相互作用分析

3.1 受力形态

选取有代表性的10 个模型，观察其在最大层间位移角下的应力云图，如图6所示。由图可知，在方钢管柱的约束下，整体都没有明显的屈曲变形，受力形态都为面内剪切变形。

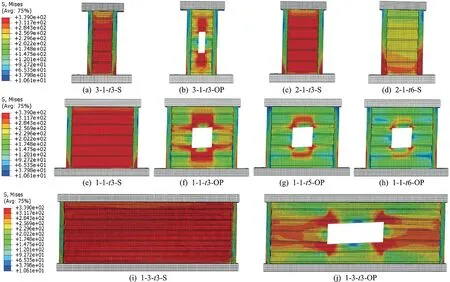
图6 应力云图Fig.6 Stress nephogram

开洞前，随着高宽比减小，应力逐渐集中于板上，当高宽比为1∶3 时板有面外扭转趋势；随着板厚增大，应力逐渐集中于边框柱上。开洞后，随着高宽比减小，应力集中区域由洞口上下侧转为左右侧；随着板厚增大，洞口周围应力显著减小。

3.2 剪力分配

3.2.1 不开洞板的剪力分配

为研究板框相互作用对不同参数钢板剪力墙的影响，对板全过程剪力占比进行分析。图7为不开洞板承担剪力比例对比图，其中θ表示层间位移角。

由图7可知，板承担剪力比例由上升变为下降直至稳定，当板开始屈服时为极值点，当柱开始屈服时比例趋于稳定。板剪力占比超过70%，说明剪力主要由板承担。当高宽比为2∶1 且板厚为2 mm 时，加载后期板剪力占比下降幅度较大。

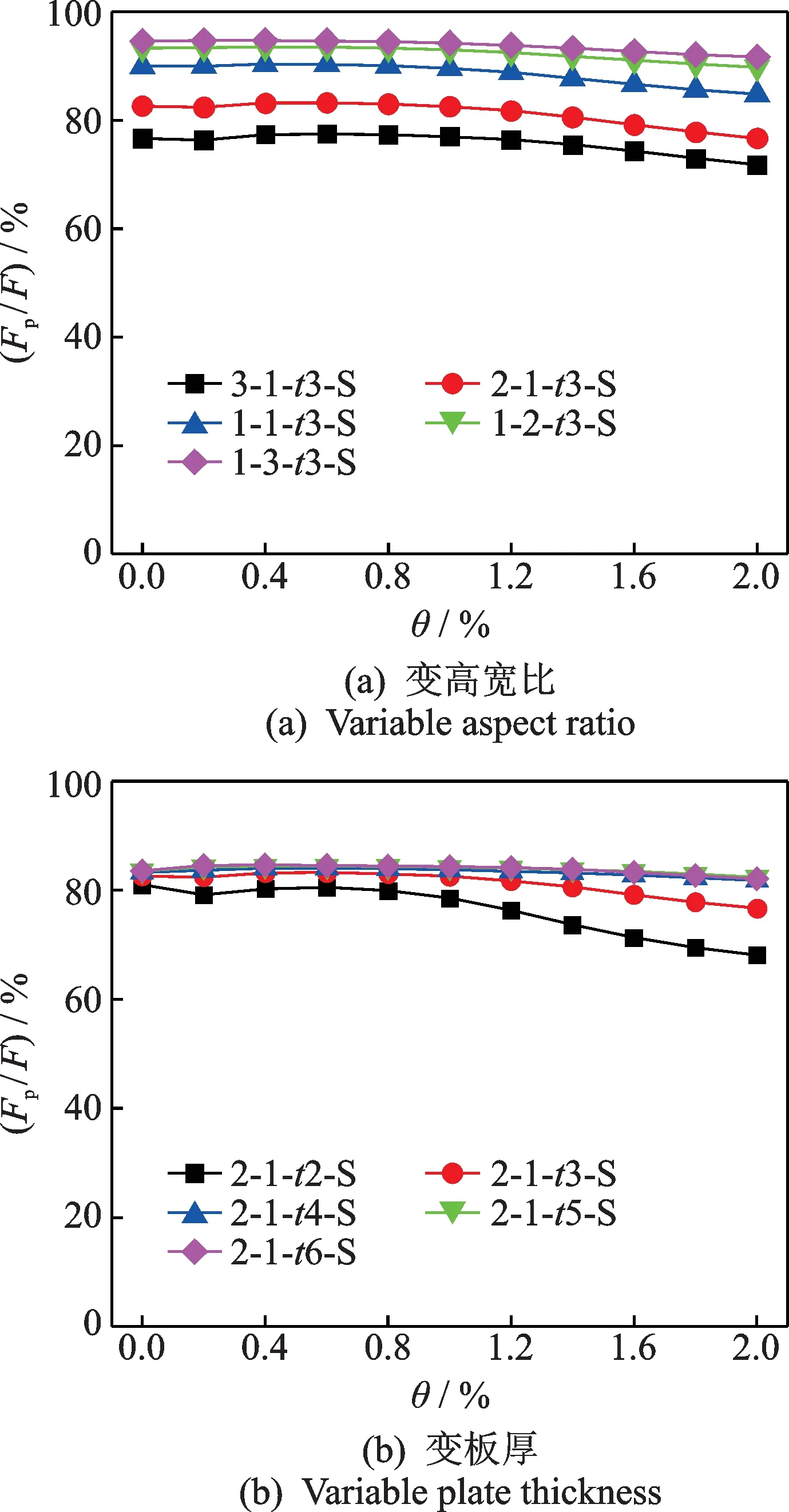
图7 不开洞板承担剪力比例Fig.7 Shear ratio of plate without opening

随着高宽比减小或板厚增大，板承担剪力比例增大，这是因为板刚度增大后，板框相互作用增强。但当高宽比小于1∶2 或板厚大于4 mm 后承载力提升较小，此时继续增大板刚度对整体力学性能影响不大。

3.2.2 开洞板的剪力分配

图8为开洞板承担剪力比例对比图。由图可知，板剪力占比只有上升段和稳定段，没有下降段，说明板与边框柱只是部分屈服，并未完全屈服。

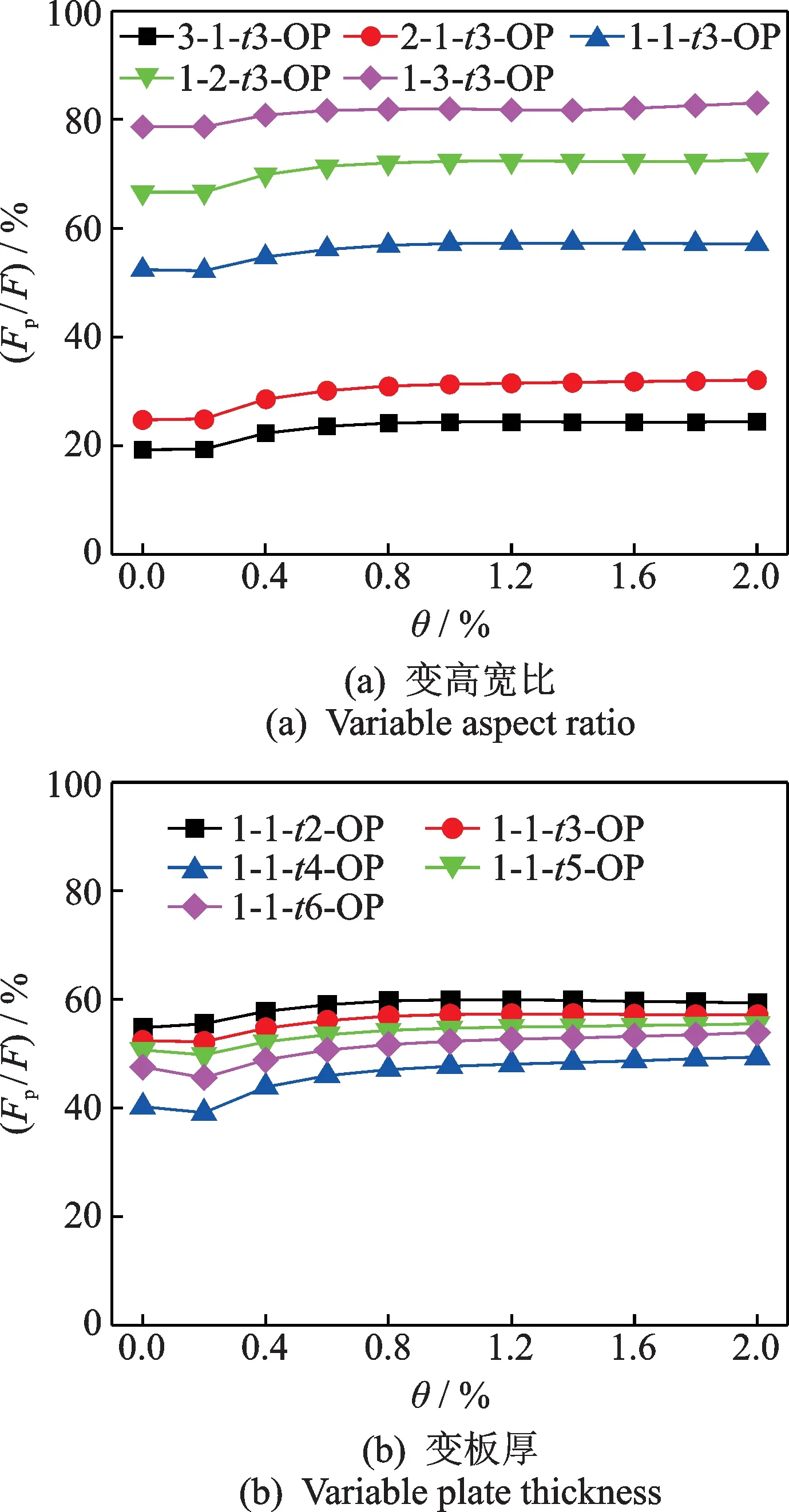
图8 开洞板承担剪力比例Fig.8 Shear ratio of plate with opening

高宽比变化对板框相互作用影响较大，当高宽比>1∶1 时，板剪力占比范围是20%～30%，此时剪力主要由边框柱承担；当高宽比≤1∶1 时，板剪力占比范围是50%～80%，此时剪力主要由板承担。这说明开洞后板刚度削弱较大，需要减小高宽比来弥补刚度损失，进而提高承载力。

板厚变化对板框相互作用影响较小，板剪力占比范围是40%～60%，但变化趋势与开洞前相反，板剪力占比随板厚增大而降低，且当板厚为4 mm 时板剪力占比最低。原因是板开洞后承载力会被削弱，虽然板厚增大会弥补开洞带来的削弱效果，但当板厚为4 mm 时开洞的削弱效果尤为明显。随着板厚增大，板剪力增长幅度小于整体剪力增长幅度，当板厚<4 mm 时，板剪力随板厚增大而增大；当板厚≥4 mm 时，板剪力增长幅度明显减小，且当板厚为4 mm 时板剪力有下降趋势，说明此时板并未完全屈服，其大部分区域仍处于弹性状态，并未完全发挥力学性能。

3.3 耗能分配

本文以模型内能变化为计算依据，其中主要根据弹性应变能与塑性变形耗能之和来衡量模型的耗能能力［17］。弹性应变能与塑性变形耗能均可从ABAQUS 有限元软件中提取，将其叠加可得弹塑性累计耗能。

各个模型的弹塑性累计耗能占比如图9所示，纵坐标表示板或边框柱耗能占总耗能的百分比。当厚度一定时，随着高宽比减小，板耗能比例逐渐增大，开洞后板耗能比例有小幅度的折减，但均在50%以上。

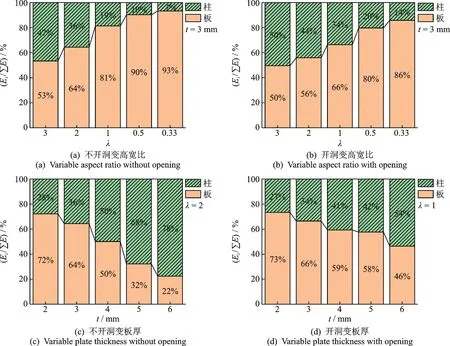
图9 累计耗能占比Fig.9 Cumulative energy consumption ratio

当高宽比一定时，随着板厚增加，板耗能比例逐渐减小，当板厚超过4 mm 后，边框柱耗能比例超过50%，开洞后变化趋势与开洞前类似。这是因为板厚越大，其对边框柱产生的附加剪力及弯矩也越大，使边框柱提前进入塑性耗能阶段，此时板屈服位移较大，且晚于边框柱进入塑性耗能阶段。因此，在满足整体承载力的条件下，板厚越小，板的利用率越高，力学性能发挥越充分。

3.4 骨架曲线对比

各个模型的骨架曲线如图10所示。当厚度一定时，随着高宽比的减小，极限承载力与初始刚度随之增大，高宽比越小趋势越明显。开洞后极限承载力与初始刚度均比开洞前低，且没有明显的屈服平台。

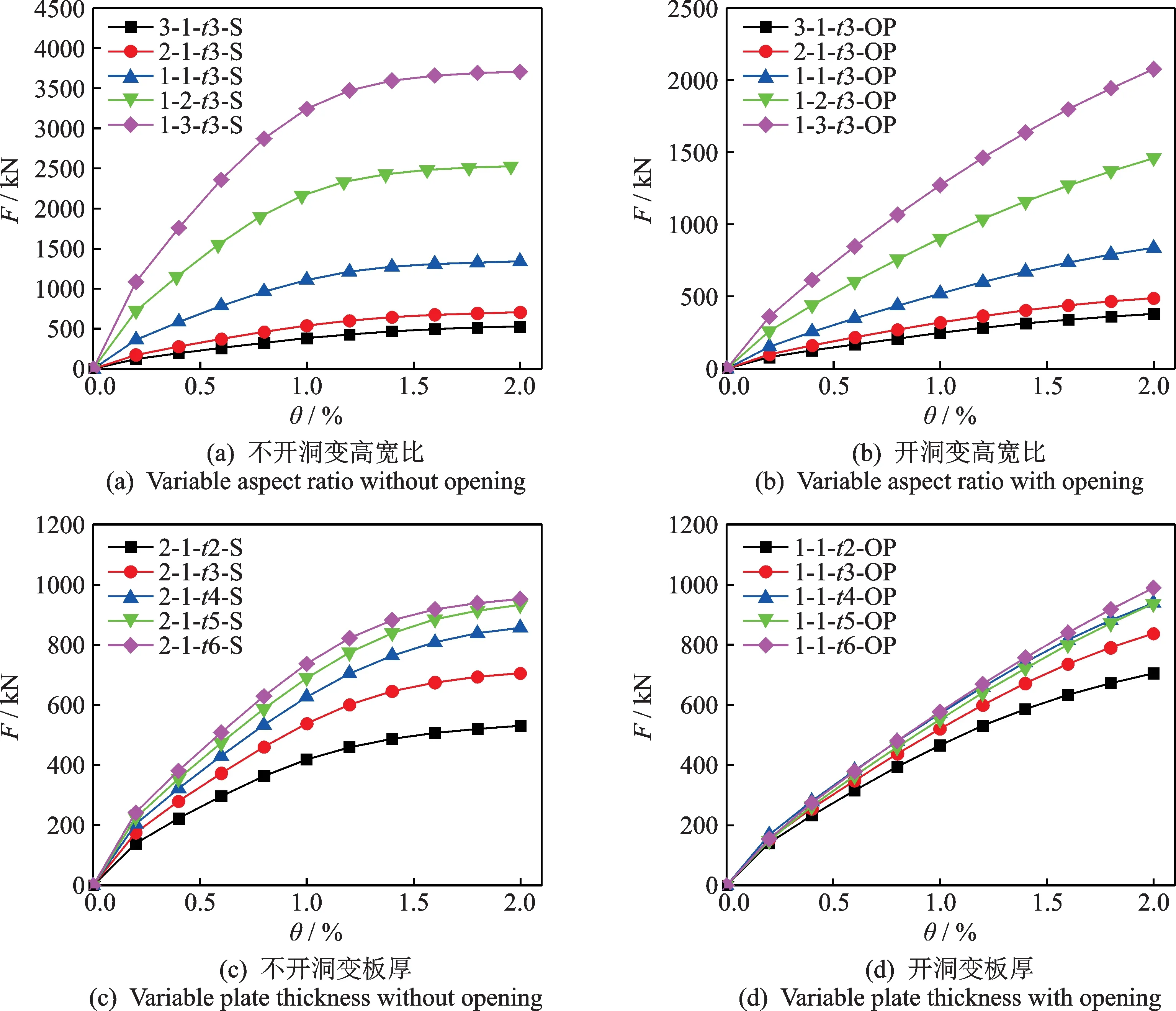
图10 骨架曲线对比Fig.10 Comparison of skeleton curves

当高宽比一定时，随着厚度的增加，极限承载力与初始刚度也随之增大，但增长幅度逐渐减小，当厚度超过4 mm 之后骨架曲线相差不大。开洞后增长幅度递减效果更明显，这说明虽然板厚增大会提升整体力学性能，但当板厚超过一定值时材料利用率会降低。

3.5 内嵌板对边框柱的影响

3.5.1 剪力对比

钢板剪力墙中的边框柱与纯框架的剪力对比如图11所示，改变高宽比对纯框架的剪力影响不大，钢板剪力墙中边框柱剪力较纯框架而言均有不同程度的提升，且随高宽比的减小而增大。开洞前当高宽比为1∶3 时剪力提升幅度最大为纯框架的2.35倍，开洞后当高宽比为1∶2 时剪力提升幅度最大为纯框架的2.68 倍，且开洞后边框柱剪力均比开洞前大。这是因为内嵌板对边框柱承载力有提升作用，内嵌板高宽比越小对边框柱提升作用越明显，而开洞后整体剪力重新分配，边框柱承担剪力比例大幅提升。

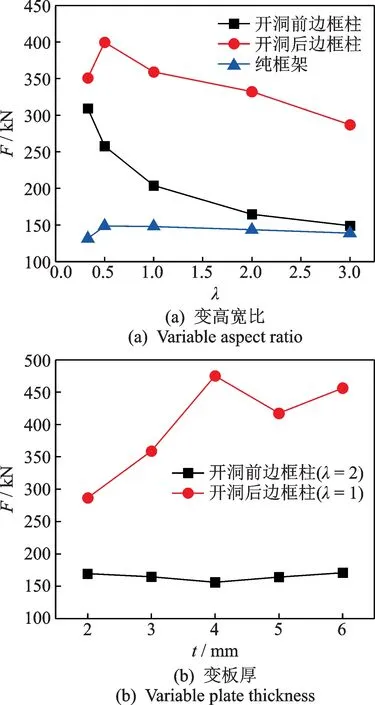
图11 剪力对比Fig.11 Comparison of shear force

开洞前改变板厚对边框柱剪力影响不大，开洞后当板厚为4 mm 时剪力提升幅度最大为3.21 倍，这说明开洞后内嵌板刚度并不是越大越好，因为开洞后板厚过大会导致应力分布不均，所以在保证整体承载力的同时选取较薄的钢板更合理。

3.5.2 耗能对比

钢板剪力墙中的边框柱与纯框架的耗能对比如图12所示，钢板剪力墙中边框柱耗能较纯框架而言均有不同程度的提高，改变高宽比对纯框架与开洞后边框柱的耗能影响不大，但开洞前边框柱的耗能随高宽比减小而逐渐增大，当高宽比为1∶3 时耗能提升幅度最大为4.49 倍，且开洞前边框柱耗能均比开洞后大，这与上述剪力对比规律相反。这是因为开洞后板刚度明显削弱，耗能主要集中于板上，边框柱耗能相对较小。

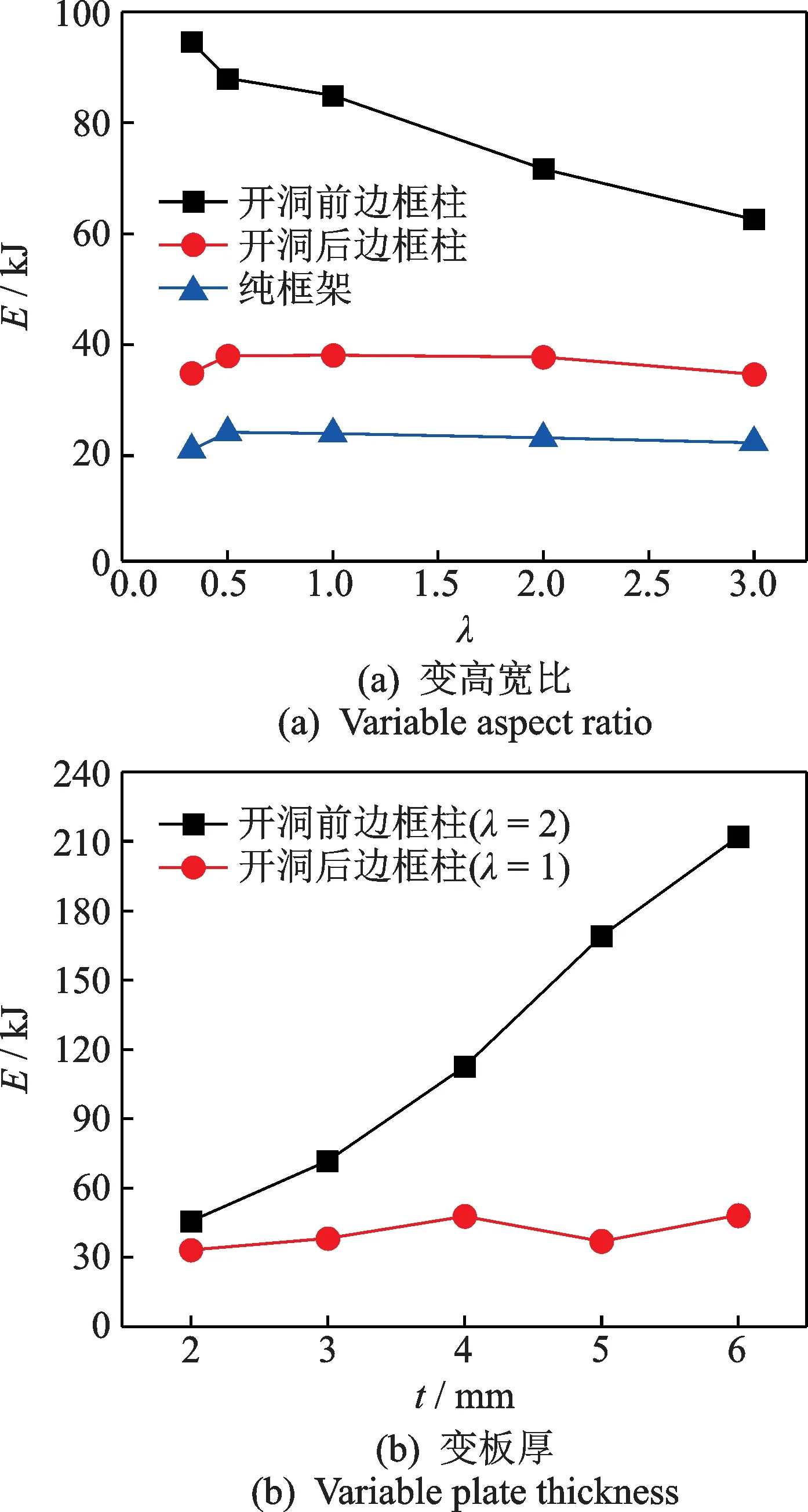
图12 耗能对比Fig.12 Comparison of energy consumption

开洞后改变板厚对边框柱耗能影响不大，开洞前当板厚为6 mm 时耗能提升幅度最大为9.15 倍，这说明开洞前板厚越大对边框柱耗能提升作用越大，但钢板剪力墙结构中钢板是主要耗能构件，应控制板厚在合理范围内，避免边框柱耗能过大导致提前发生破坏。

3.5.3 板-边柱相互作用与开洞影响分析

内嵌板与边框柱的组合不是简单叠加，而是起到了相互促进的作用。边框柱对内嵌板具有约束作用，横波钢板的两侧波形截面被约束后，受力机理不同于平钢板的拉力带屈服，而是趋于全截面屈服，应力分布均匀，力学性能发挥更充分；内嵌板对边框柱具有提升作用，板受力时会对边框柱产生附加剪力及弯矩，使边框柱承载力及耗能增大，更容易达到塑性阶段，材料利用率也更高。

剪力墙开洞后会降低其抗侧刚度及强度，受力时容易在洞口角点形成应力集中，导致应力不均匀分布，且洞口会出现沿对角线拉伸变形趋势，不利于板内部应力传递，使板不能充分发挥其力学性能。因此开洞后，板承载力与耗能会因高宽比和板厚的差异而有不同程度的降低，柱承载力与耗能会因此而提高，但整体承载力与耗能大幅降低，说明开洞对剪力墙的削弱作用较为明显。而且开洞后受力主要集中于洞口角点薄弱区，板厚越大其屈服位移越大，材料利用率越低，板框相互作用效果越差，此时柱应力反而较大。因此开洞板的厚度不宜过大。

3.6 增幅比

定义增幅比α来衡量剪力墙力学性能提升效率，计算公式如下：

式中Xi表示衡量剪力墙力学性能的特征参数；Xi−1表示特征参数在上一个高宽比或板厚时的取值。

当α＞1 时表明性能提升，值越大则提升效率越高；当α＜1 时表明性能下降，值越小则降低效率越高。下文以极限荷载增幅比（αfi）、初始刚度增幅比（αki）、延性系数增幅比（αμi）以及板耗能增幅比（αpi）作为参照。

如图13所示，图中四边形对应的角点是板的高宽比或板厚，内部边界线上的点对应着在不同高宽比或板厚下的增幅比。开洞前当高宽比为1∶1 且板厚为3 mm 时提升效率最高，开洞后当高宽比为1∶2且板厚为4 mm 时提升效率最高，这说明板刚度并不是越大越好，其与边框柱之间存在合理的匹配关系，在保证足够承载力及刚度的条件下板厚较小时板框相互作用效果较好。同时开洞削弱了板的刚度，需要减小高宽比及适当增加板厚来保证板与边框柱之间具有较高的配合度，从而使整体力学性能最优。

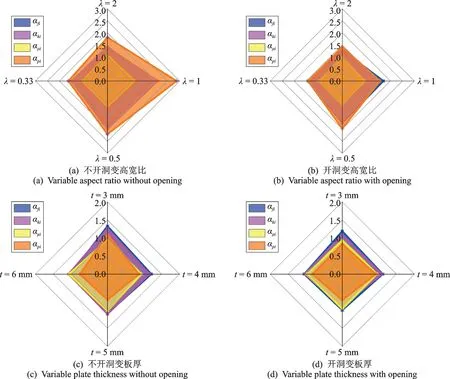
图13 增幅比对比Fig.13 Comparison of growth rate

4 理论模型

4.1 改进PFI 模型

Sabouri-Ghomi 等［10］基于剪切屈曲理论提出PFI 模型设计方法，将板和框架的受力过程分为两个阶段，即弹性阶段和塑性阶段，整体承载力可由板和框架叠加得到。但此模型对应的屈服特征点仅考虑剪切屈服起始点，并未考虑全截面屈服起始点，因此不能直接适用于有明显弹塑性阶段的受力过程。

基于本文带方钢管柱的横波钢板剪力墙受力特点，引入弹塑性变形阶段，提出考虑屈服后屈曲的改进PFI 模型，综合考虑板框相互作用对剪力墙体系力学性能的贡献。

4.1.1 基本假定

（1）边框梁为刚性梁，不考虑其变形影响；

（2）边框柱刚度足够大以至于计算板剪切变形时可以忽略边框柱的位移；

（3）忽略整体弯曲应力对剪切屈服应力的影响；

（4）板和边框柱表现为理想弹塑性；

（5）忽略开洞对边框柱屈服位移及承载力的影响；

（6）为简化模型，假定板和边框柱同时进入弹塑性阶段；

（7）叠加原理可以适用。

由PFI 理论可知，板和边框柱的荷载-位移曲线可以分别独立计算，则能得到板和边框柱的强度和刚度，并能得知它们对整体承载力的贡献。与传统PFI 模型相比，改进PFI 模型更适用于无明显屈曲变形的横波钢板剪力墙。如图14所示。

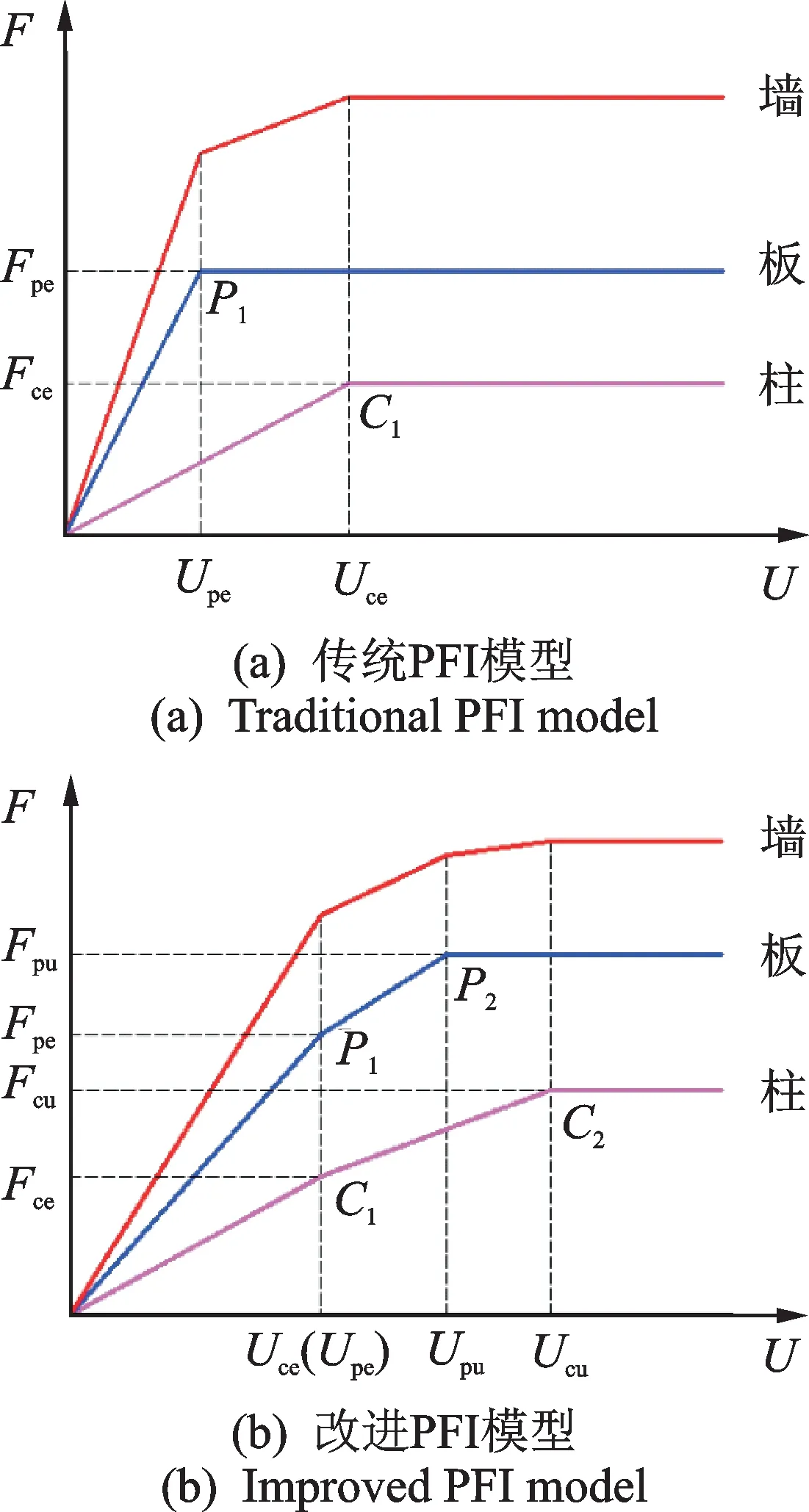
图14 PFI 模型计算荷载-位移曲线的示意图Fig.14 Schematic diagram of load-displacement curve calculated by PFI model

4.1.2 框架的荷载-位移曲线计算

框架理想化模型如图15所示，假定弹塑性阶段只有柱脚形成塑性铰，塑性阶段柱顶和柱脚均形成塑性铰。开洞后边框柱只考虑弹性和弹塑性阶段，不考虑塑性阶段。

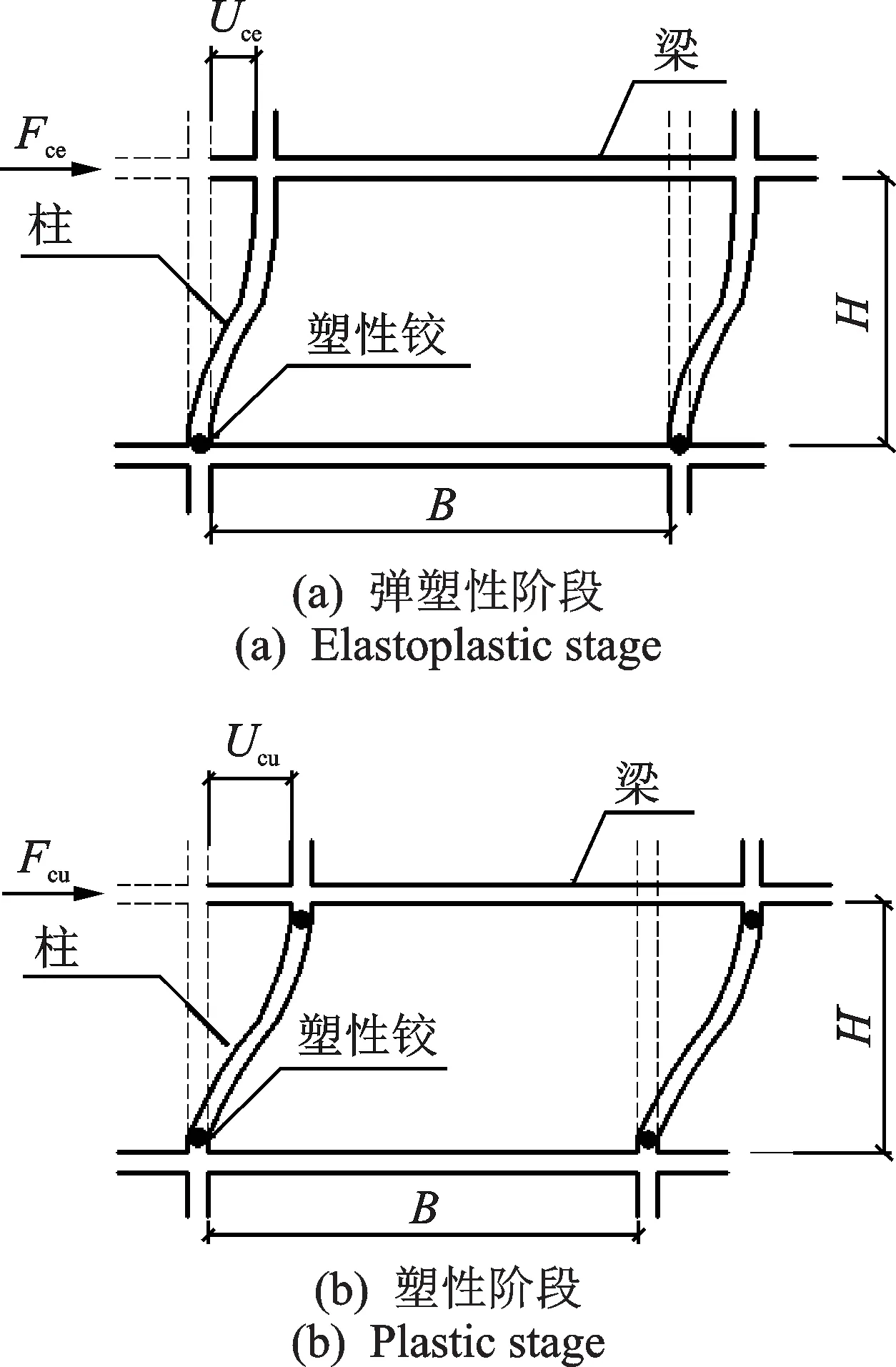
图15 框架理想化模型Fig.15 Idealized model of frame

各特征点承载力和对应位移的计算如下式所示：

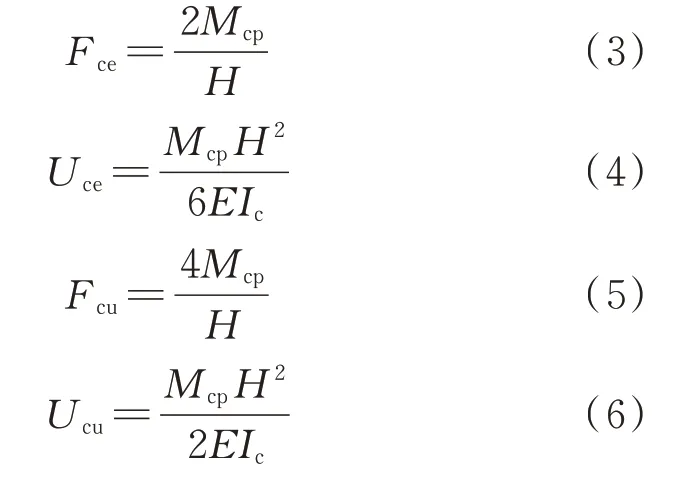
式中Fce为边框柱剪切屈服点承载力；Mcp为边框柱塑性铰区域对应的截面塑性弯矩值；H为板高度；Uce为边框柱剪切屈服点位移；Ic为边框柱强轴抗弯刚度；Fcu为边框柱全截面屈服点承载力；Ucu为边框柱全截面屈服点位移。

4.1.3 板的荷载-位移曲线计算

板理想化模型如图16所示，阴影部分为剪切屈服区域，假定弹塑性阶段为板部分区域剪切屈服，塑性阶段为板全截面剪切屈服。开洞后板只考虑弹性阶段和弹塑性阶段，不考虑塑性阶段。

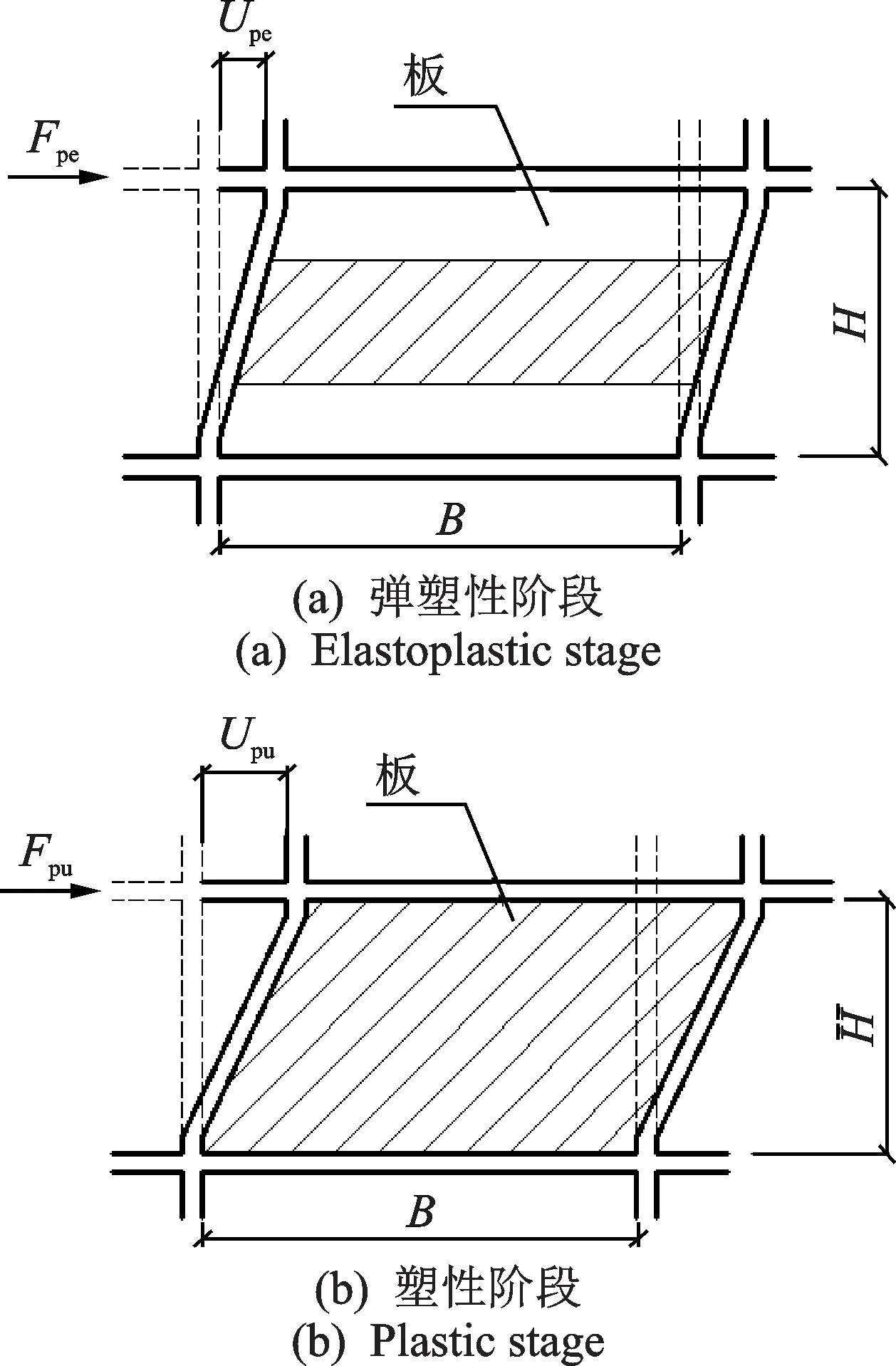
图16 板理想化模型Fig.16 Idealized model of plate

由于板在达到最大层间位移角前未发生屈曲变形，其极限承载力会因板框相互作用的促进而提升，应在原有剪切屈服承载力的基础上乘以超强系数［18］。基于假定，板与边框柱的剪切屈服点位移相同，而板的全截面屈服点位移则与其高宽比和厚度有关。

各特征点承载力和对应位移的计算如下所示：

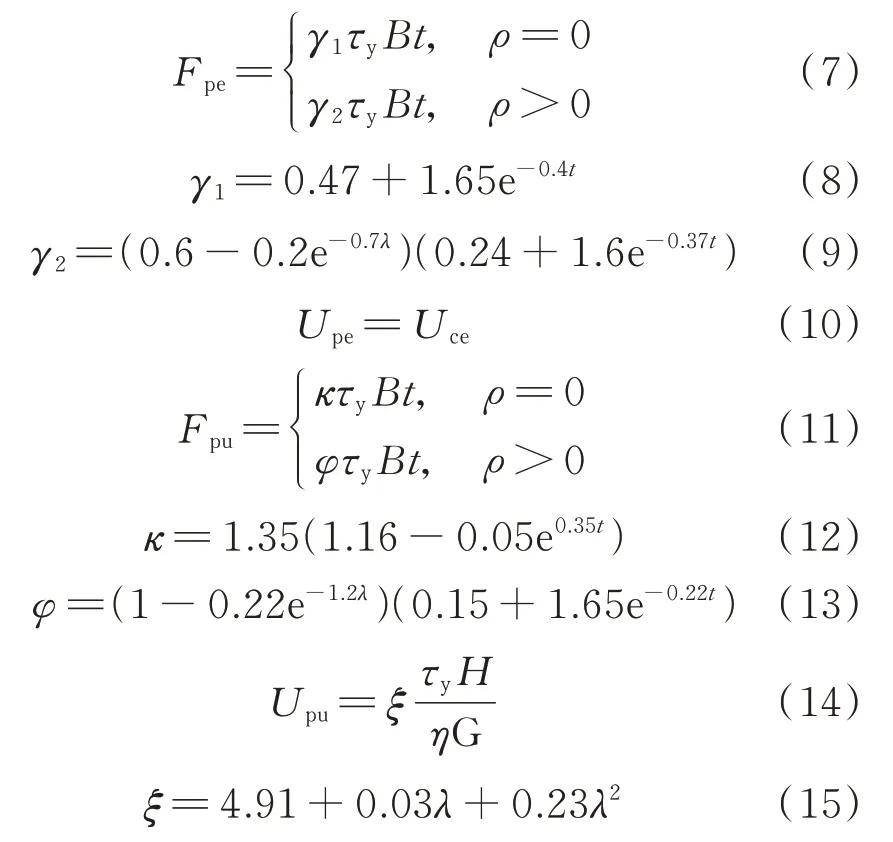
式中Fpe为板剪切屈服点承载力；B为板宽度；γ1为不开洞剪切屈服折减系数；γ2为开洞剪切屈服折减系数；τy为剪切屈服应力，τy=ρ为开洞率；Upe为板剪切屈服点位移；η为波形形状折减系数，η=，其中a为平直边长度，b为斜边长度，β为波角；G为钢材弹性剪切模量，G=；Fpu为板全截面屈服点承载力，开洞后为极限承载力；κ为超强系数；φ为开洞承载力折减系数；Upu为板全截面屈服点位移；ξ为相互作用系数。

4.2 改进PFI 模型对比验证

图17为改进模型与传统模型对比图，其中A 点代表弹塑性拐点，B 点代表塑性拐点，C 点代表极限荷载点。由于开洞后不考虑塑性阶段，D 点代表极限位移点。由图可知，改进PFI 模型比传统模型吻合度更高，开洞前曲线经历了弹性、弹塑性和塑性阶段，最后板与边框柱均全截面屈服；开洞后曲线经历了弹性和弹塑性阶段，最后板与边框柱均未全截面屈服。

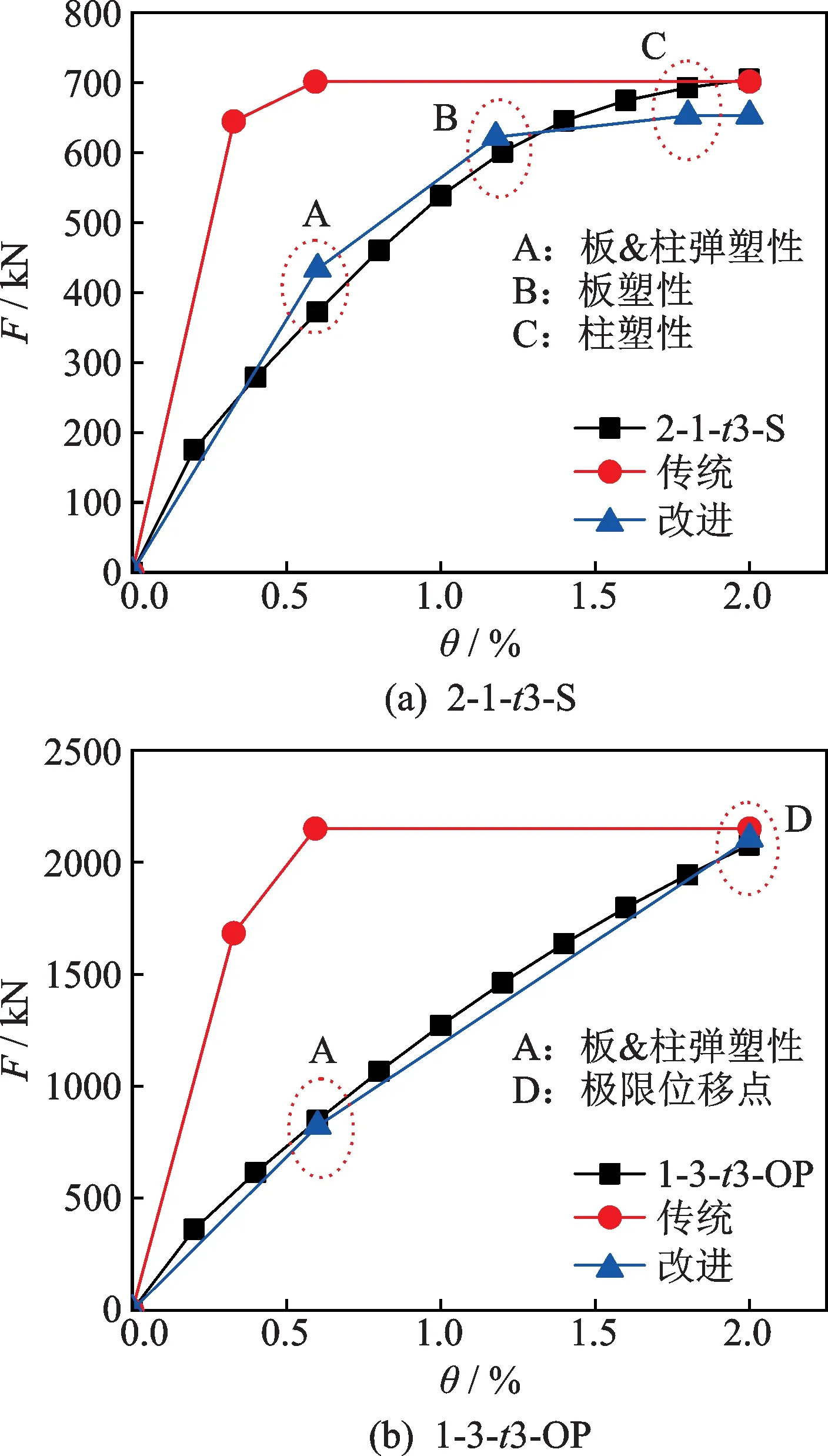
图17 改进模型与传统模型对比Fig.17 Comparison between improved model and traditional model

通过分析变参模型，将其在传统PFI 模型与改进PFI 模型中特征点的取值进行对比。由于传统PFI 模型对于开洞剪力墙来说适用性较低，因此对于开洞模型而言，只考虑其在改进PFI 模型下的特征点取值。

由表3可知，特征点对应承载力计算值与模拟值的误差大部分在10%以内，在弹塑性初始点有个别值由于曲线斜率较小，误差超过10%，但对整体影响不大。因此改进PFI 模型能较为准确地预测剪力墙受力全过程，可为工程设计提供参考。

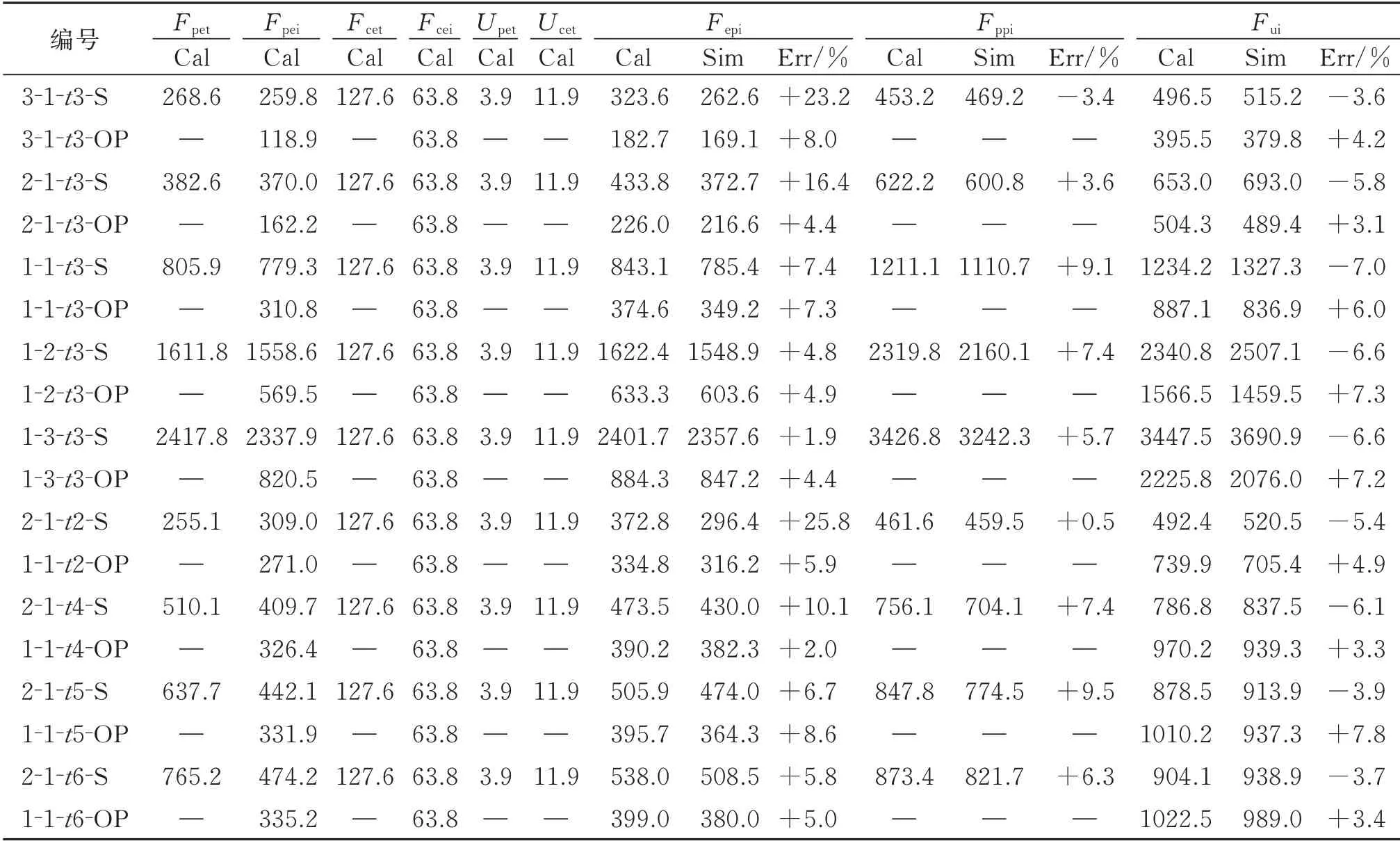
表3 改进PFI 模型与传统PFI 模型特征点对应表Tab.3 Correspondence table of characteristics between improved PFI model and traditional PFI model

5 结 论

通过数值模拟对23 个横波钢板剪力墙变参模型的力学性能展开分析，研究内嵌波形板与边框柱相互作用对剪力墙力学性能的影响，得出下列结论：

（1）数值模拟方法可信度较高，横波钢板剪力墙边框柱约束不足时易发生面外屈曲破坏，板未充分发挥力学性能；边框柱约束较大时能有效抑制板屈曲变形，受力形式为面内剪切变形，内嵌板与边框柱协同工作良好。开洞前应力主要集中于板上，开洞后应力集中于洞口角点周围及柱上。

（2）有限元变参模型结果表明，开洞前剪力主要由板承担，随着高宽比减小或板厚增大，板承担剪力比例增大，但增幅逐渐减小。开洞后随着高宽比增大或板厚增大，边框柱承担剪力比例增大。高宽比变化对剪力分配影响较大，板厚变化对耗能分配影响较大，板厚越大边框柱耗能比例越大，板利用率越低。在满足整体承载力的条件下，板厚越小，板利用率越高，力学性能发挥越充分。

（3）相比于纯框架，内嵌板对边框柱抗剪承载力及耗能能力提升效果明显，其抗剪承载力提升幅度随高宽比减小而增大，其耗能能力提升幅度在开洞前随高宽比减小与板厚增大而增大。定义增幅比来衡量力学性能提升效率，开洞前当高宽比为1∶1 且板厚为3 mm 时提升效率最高，开洞后当高宽比为1∶2 且板厚为4 mm 时提升效率最高。

（4）基于传统PFI 模型，引入弹塑性变形阶段，提出考虑屈服后屈曲的改进PFI 模型，综合考虑板框相互作用对剪力墙体系的力学性能的贡献。理论推导并拟合出内嵌波形板与边框柱的各阶段承载力及位移公式，并将理论计算值与本文变参模型对应特征点承载力进行对比，误差基本在10%以内，能较好预测剪力墙受力过程，具有工程参考价值。