谐波注入在电动汽车动力总成电磁振动抑制中的应用

丁俊杰，陈天宁，方江龙，符俊杰，唐 旭

（西安交通大学机械工程学院，陕西 西安 710049）

引 言

随着电动化进程的推进，电动汽车的NVH 性能越发受到关注，提高汽车的舒适性，降低动力总成的振动和噪声变得愈发重要。从电磁振动的角度来看，引起振动和噪声的电磁力分为两个分量：径向力和转矩脉动，即切向力［1］。虽然径向力是引起电机振动的一个关键原因［2-3］，但是针对电机-减速器一体化驱动系统而言，转矩脉动频率容易与总成的扭转模态频率耦合，引起总成扭转振动［4-6］；同时由于电动汽车传动系统中一般不存在扭转减振器、飞轮等被动减振和隔振部件，导致振动传递到整车上，极大地降低了乘坐舒适性。

减小转矩脉动的方法分为两类：电磁设计方法和控制方法。电磁设计方法通过优化电机拓扑、斜极或斜槽形式来减小转矩脉动［7-9］，但这种方法通常会影响到电机性能，加工复杂且成本较高。相反，控制方法通过控制策略来改善电流波形，比电磁设计方法更容易实现。因此，本文主要采用谐波电流注入控制方法来减小转矩脉动。

对于从电流谐波方面控制电磁噪声，早期研究主要对电机d，q轴电流或电压进行补偿控制，从而消除5，7 次等谐波，减小电机转矩脉动和电磁噪声［10-12］。但这种方法在电机控制策略中增设了谐波电流检测和提取模块、自适应滤波器、补偿量实时计算模块等，大大增加了电机控制策略的复杂性，且如需对更髙次谐波成分进行控制，控制算法将更加复杂。因此，有学者提出，首先通过转矩脉动模型来预测电机的转矩脉动大小，然后采用优化算法来定位所需注入的谐波电流，使预测的转矩脉动最小［13-15］。如文献［13］提出了一种基于拉格朗日算子的谐波电流优化方法；文献［14］提出了一种基于神经网络的自学习方法来优化谐波电流；文献［15］利用遗传算法对谐波电流的幅值和相位进行优化。然而永磁同步电机是高度非线性系统，上述文献都是基于电机电气模型来得到转矩脉动模型，没有考虑电机运行时参数的变化以及磁饱和等非线性因素的影响，导致转矩脉动预测不准确或优化效果不佳；同时，尚未有文献直接分析谐波注入方法对电磁振动的改善效果。

针对上述问题，本文建立场路耦合电磁仿真分析模型，该模型能够反映电机参数的变化以及磁饱和等非线性因素的影响，通过仿真得到电机的电磁激励并进行分析，结合动力总成的振动试验，重点探究转矩脉动对电磁振动的影响。在此基础上，采用谐波电流注入方法来抑制电机的转矩脉动，利用RBF 神经网络代理模型和遗传算法结合的方法来优化电流参数，并通过振动测试验证了谐波注入方法对降低电磁振动的有效性。

1 基本原理

1.1 PMSM 转矩脉动模型

根据磁共能模型，永磁同步电机产生的转矩为：

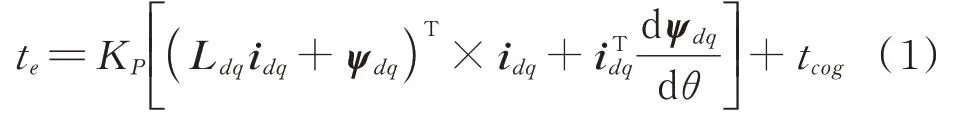
式中te为电机产生的总转矩，包括直流转矩和谐波转矩；Ldq为dq轴的电感矩阵；ψdq和idq为dq轴的磁链矢量和电流矢量；θ为转子电角度；tcog为齿槽转矩。坐标变换采用恒幅值变换，KP为3P/2，P为电机的极对数。在式（1）中，忽略了电感谐波。从该公式可分析出转矩谐波主要来源于电流谐波、磁链谐波以及齿槽转矩。

为了对永磁同步电机转矩谐波进行建模，将定子电流和磁链用傅里叶级数表示，如下式所示：

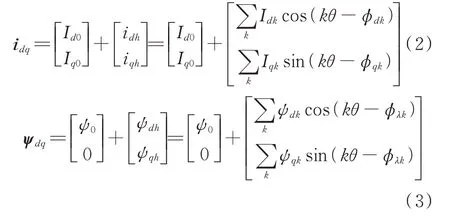
根据文献［11］，齿槽转矩公式为：

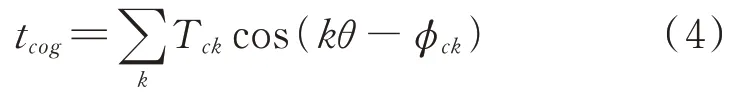
各参数的定义如下：

1）Id0和Iq0为dq轴电流平均值；idh和iqh为dq轴谐波电流；Idk和Iqk为dq轴k次谐波电流分量；ϕdk和ϕqk为相应电流谐波的相位。

2）ψ0为d轴平均磁链；ψdh，ψqh为dq轴磁链谐波；ψdk和ψqk为dq轴k次磁链谐波分量；ϕλk为k次磁链谐波的相位。

3）Tck和ϕck为齿槽转矩中k次谐波的幅值和相位。

将式（2）～（4）代入式（1），可以得到永磁同步电机产生的总转矩的详细模型。具体来说，可以将PMSM 产生的总转矩te解耦为直流转矩T0和谐波转矩th，如下式所示：

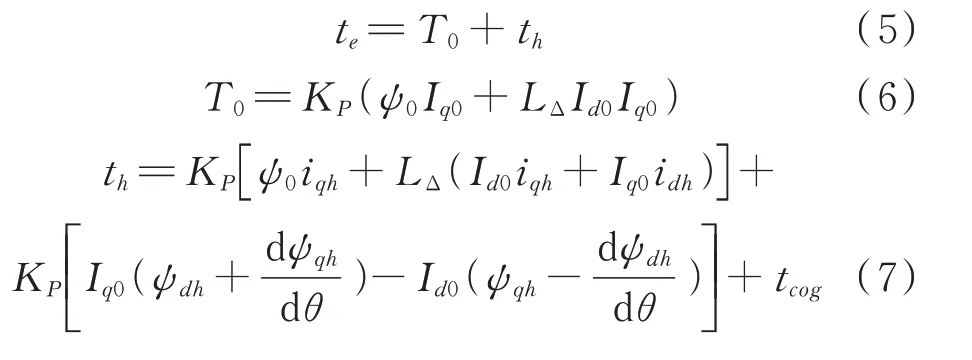
上述公式中，由于定子电流谐波与磁链谐波相互作用产生的谐波转矩分量很小，因此可以被忽略。将式（2）～（4）代入式（1）得到的转矩谐波模型如下：

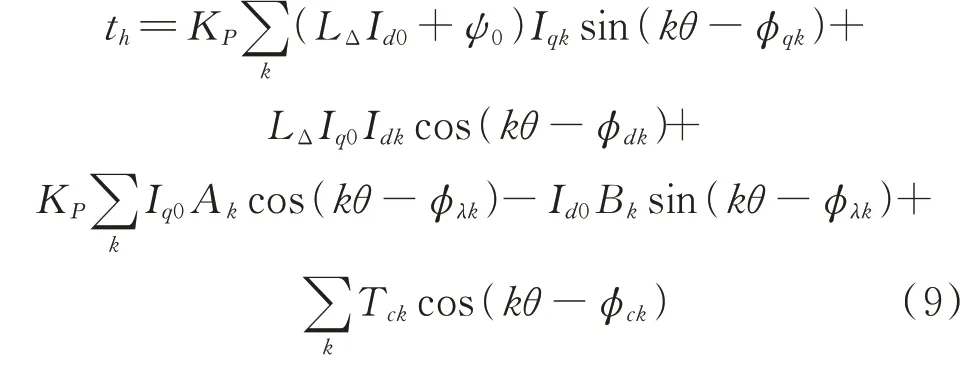
式中Ak和Bk为：

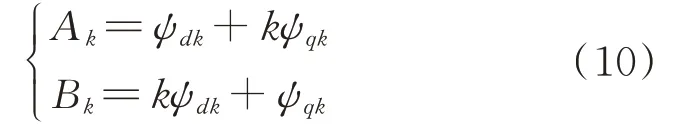
在永磁同步电机中，转矩谐波次数k主要为6，12，18，24 等［12，15］。在本文中，起主要作用的谐波转矩为12 次，由于本文所涉及到的驱动电机极对数为4，故称为48 阶转矩脉动。

1.2 谐波电流注入原理

根据公式（9），可将转矩脉动分为三部分，即谐波电流引起的转矩脉动、永磁体磁链谐波引起的转矩脉动以及齿槽转矩脉动。由于永磁同步电动机电磁设计方案确定后，无法控制或改变永磁体磁链和齿槽转矩。因此，后两部分是不可控的，即在理想正弦电流下仍存在，可称其为固有转矩脉动，因此永磁同步电机产生的转矩脉动可以看作固有转矩脉动和谐波电流导致的额外转矩脉动的叠加。将转矩脉动绘制在矢量平面上，用向量可以简洁地表示转矩脉动的特性，如图1所示，谐波电流产生的转矩脉动形成一个以固有转矩脉动为中心的圆轨迹。此时圆的半径与谐波电流的幅值成正比，圆的相位也随着谐波电流相位的变化而变化。减小转矩脉动的目标是找到最优的定子电流，使总的转矩脉动的幅值最小，并通过适当的控制方法注入定子谐波电流。

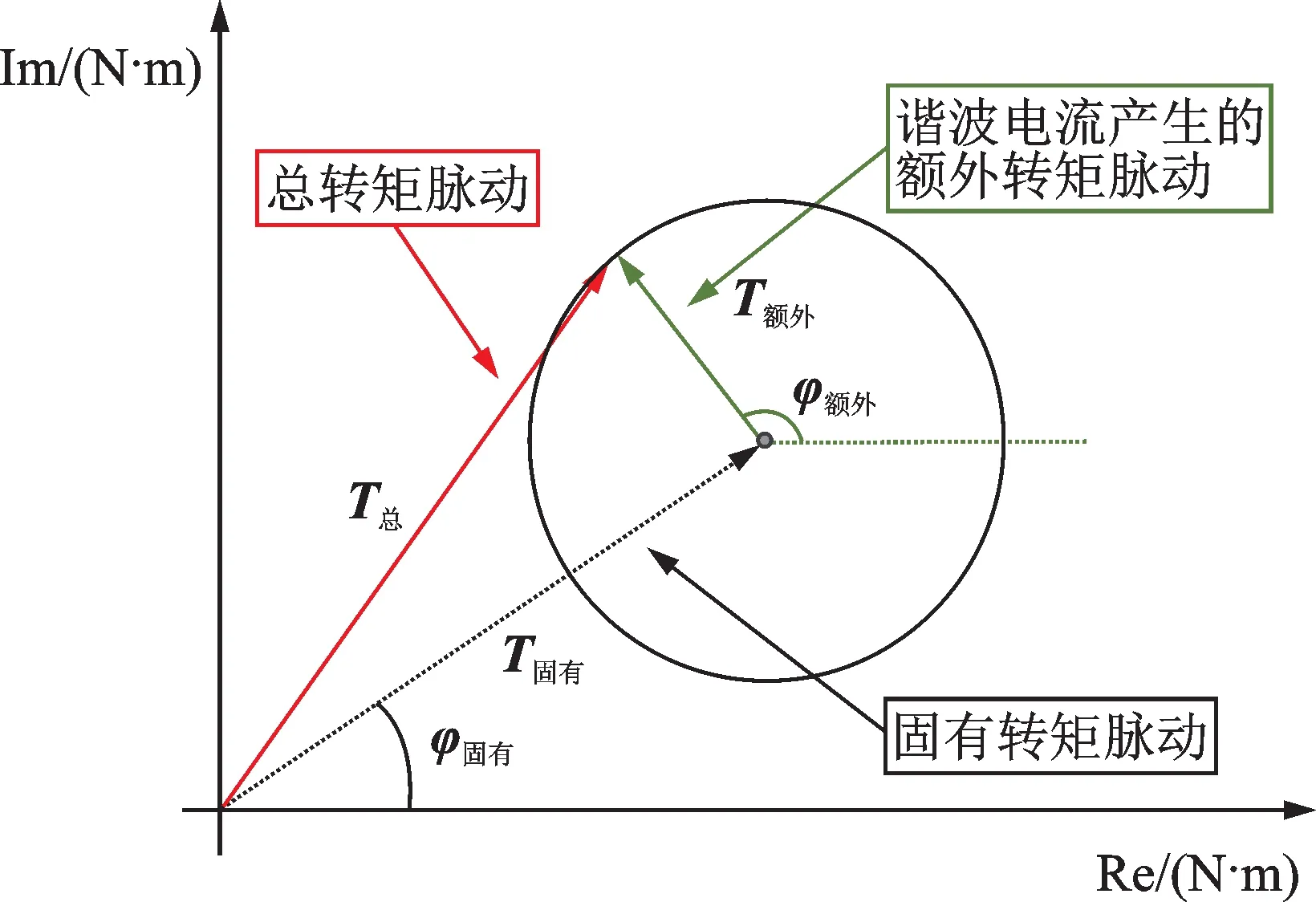
图1 转矩脉动矢量图Fig.1 Schematic diagram of torque ripple vector

2 动力总成电磁激励仿真分析及试验

2.1 动力总成电磁激励分析

本文以某新能源汽车集中式电驱动动力总成为研究对象，驱动电机为8 极48 槽内置式永磁同步电机（IPMSM），其二维电磁模型如图2所示，电机主要参数如表1所示。

图2 永磁同步电机电磁仿真模型Fig.2 Electromagnetic simulation model of permanent magnet synchronous motor

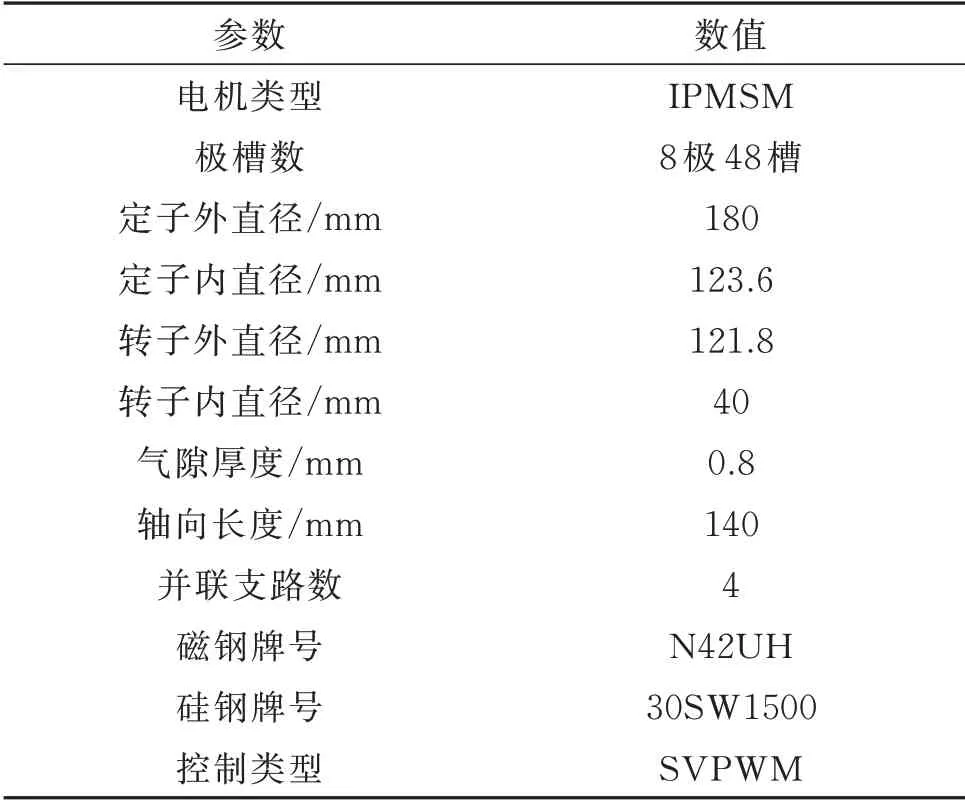
表1 电机主要参数Tab.1 Main parameters of motor

本文采用场路耦合的方法来考虑电机参数的变化以及磁饱和等非线性因素。联合仿真模型如图3所示，在Simplorer 软件中搭建电机功率回路模型，在Maxwell 软件中建立电机电磁模型，在Matlab/Simulink 搭建电机控制回路模型。其中电磁模型能够考虑电机漏磁、磁场饱和、电枢反应及损耗对电机性能的影响；控制系统控制电机的输入，电机将三相电流、转速、位置、转矩等信息反馈到控制系统中，其控制策略框图如图4所示。

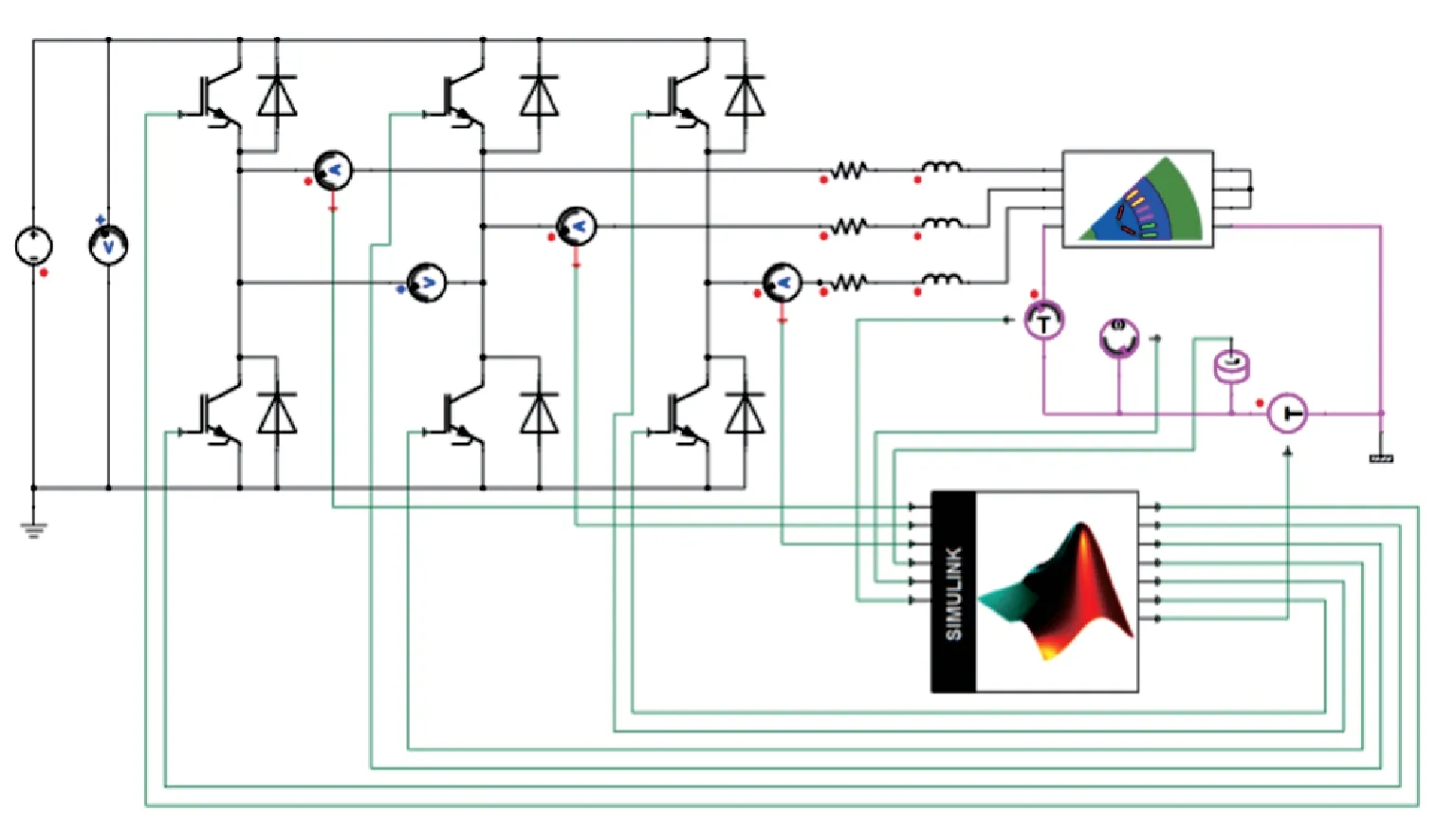
图3 永磁同步电机联合仿真模型Fig.3 Co-simulation model of permanent magnet synchronous motor

图4 永磁同步电机控制策略框图Fig.4 Block diagram of permanent magnet synchronous motor control strategy

电动汽车动力总成的电磁振动主要由电机运行时气隙中谐波磁场相互作用产生的电磁力波引起。利用Maxwell 定律可以计算出作用于定子铁心内表面单位面积上的径向电磁力Pr和切向电磁力Pt，如下式所示：

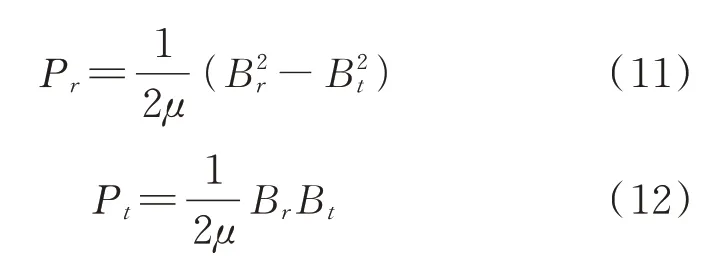
式中μ为真空磁导率，μ=4×10−7H/m；Br，Bt分别为径向和切向气隙磁密。

以转速为1000 r/min 为例，控制电路采用空间矢量脉宽调制（SVPWM）策略，负载为180 N·m，仿真分析转子在不同位置时电机气隙中的径向电磁力和切向电磁力如图5所示。

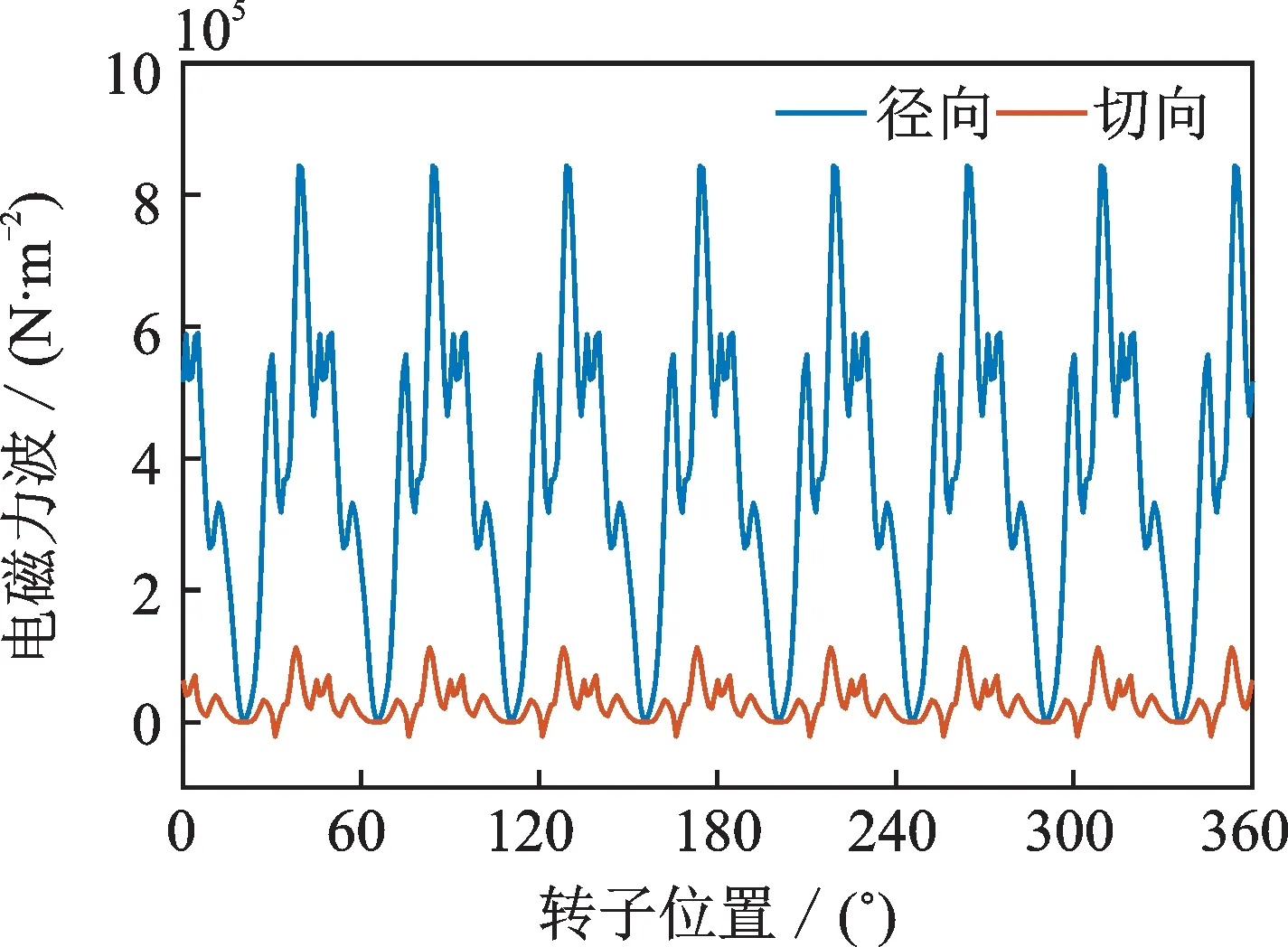
图5 电磁力仿真结果图Fig.5 Simulation results of electromagnetic force

根据电磁力仿真结果，径向电磁力和切向电磁力均呈周期性变化，径向力峰值为844110 N/m²，切向力峰值为112712 N/m²，由于切向力幅值较小，且电机结构对称，许多学者在分析电磁振动时忽略了切向力的作用，认为径向力是产生电磁振动的主要来源。然而对于集中式动力总成，当电机和减速器集成在一起时，整个系统不再是对称的圆柱结构，因此系统振动特性会发生变化。在实际工作过程中，切向力对动力总成的振动噪声有很大的影响，因此本文重点研究了切向力对电磁振动的影响。

切向电磁力分为局部切向力和整体切向力。施加在定子齿面上的局部切向力主要引起径向振动，但由于幅值远小于径向力，对振动噪声的贡献量可忽略不计。而整体切向力，即转矩脉动，会导致电机的扭转振动，对噪声的影响不可忽视［16-17］。通过对气隙中的切向力进行积分，可以得到电机的转矩，即：

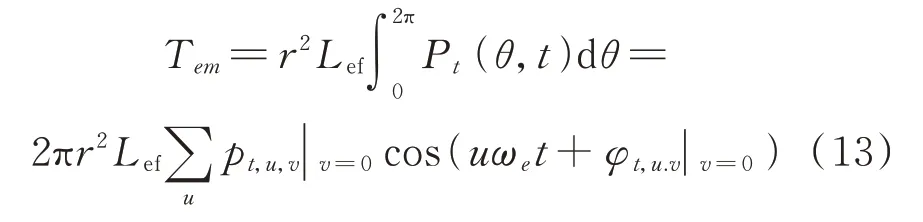
式中r为积分路径的半径，Lef为有效长度，pt，u，v为t时刻空间阶为v，时间阶为u的切向力，ωe为电角度，φt，u.v为相应的相位角。该式表明，电机的输出转矩是由空间阶v=0 的切向力产生的，其中，时间阶u=0 的切向力产生恒定转矩，而u≠0 的切向力谐波形成转矩脉动。图6展示了转速为1000 r/min时的电磁转矩波形图和频谱图，由频谱图可知，该转矩谐波幅值最高的阶次为48 阶。

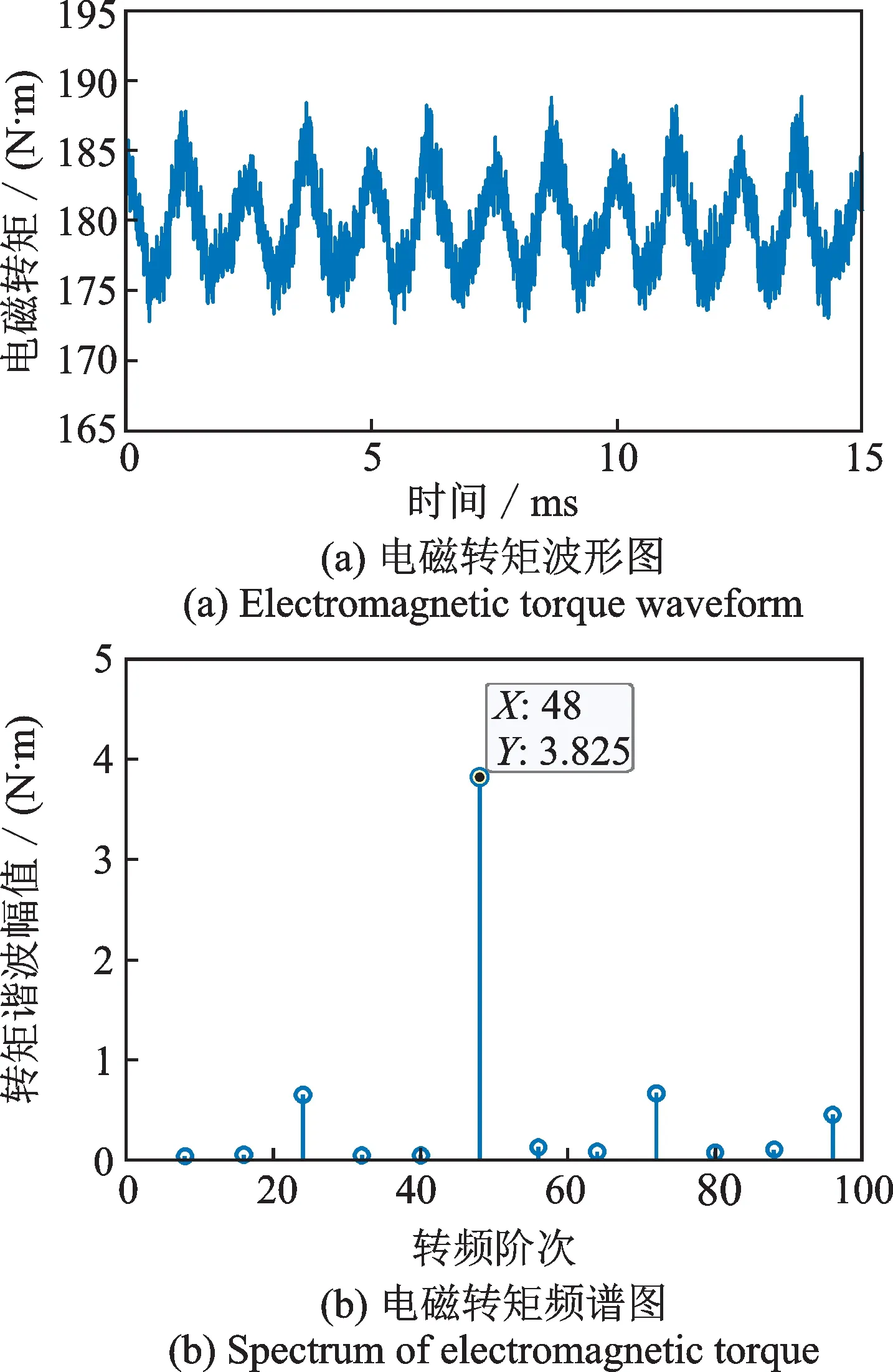
图6 电磁转矩波形图和频谱图Fig.6 Waveform and spectrum of electromagnetic torque

2.2 动力总成振动测试试验

在测试台架上对某集中驱动式纯电动车动力总成进行振动试验，动力总成通过模拟整车悬置的方式安装在台架上，利用控制器来调节电机输入转速的变化，电机则通过冷却水来控制温度。实验台架的负载电机通过传动轴及联轴器连接到减速器的输出轴端；同时，利用负载电机在减速器输出端施加反方向的负载扭矩来模拟电驱动总成在整车运行时载荷的变化。测试系统示意图如图7所示，采用Test.lab 信号分析处理系统来采集测点振动信息，测点布置在电机壳体下方，通过加速度传感器来获得其表面法向振动加速度，测点位置如图8所示。通过测试发现，动力总成在全油门工况下主要有24，48，96 阶电磁振动问题，且48 阶振动相对突出。图9展示了电机转速在500～5000 r/min 的动力总成48 阶振动测试结果。

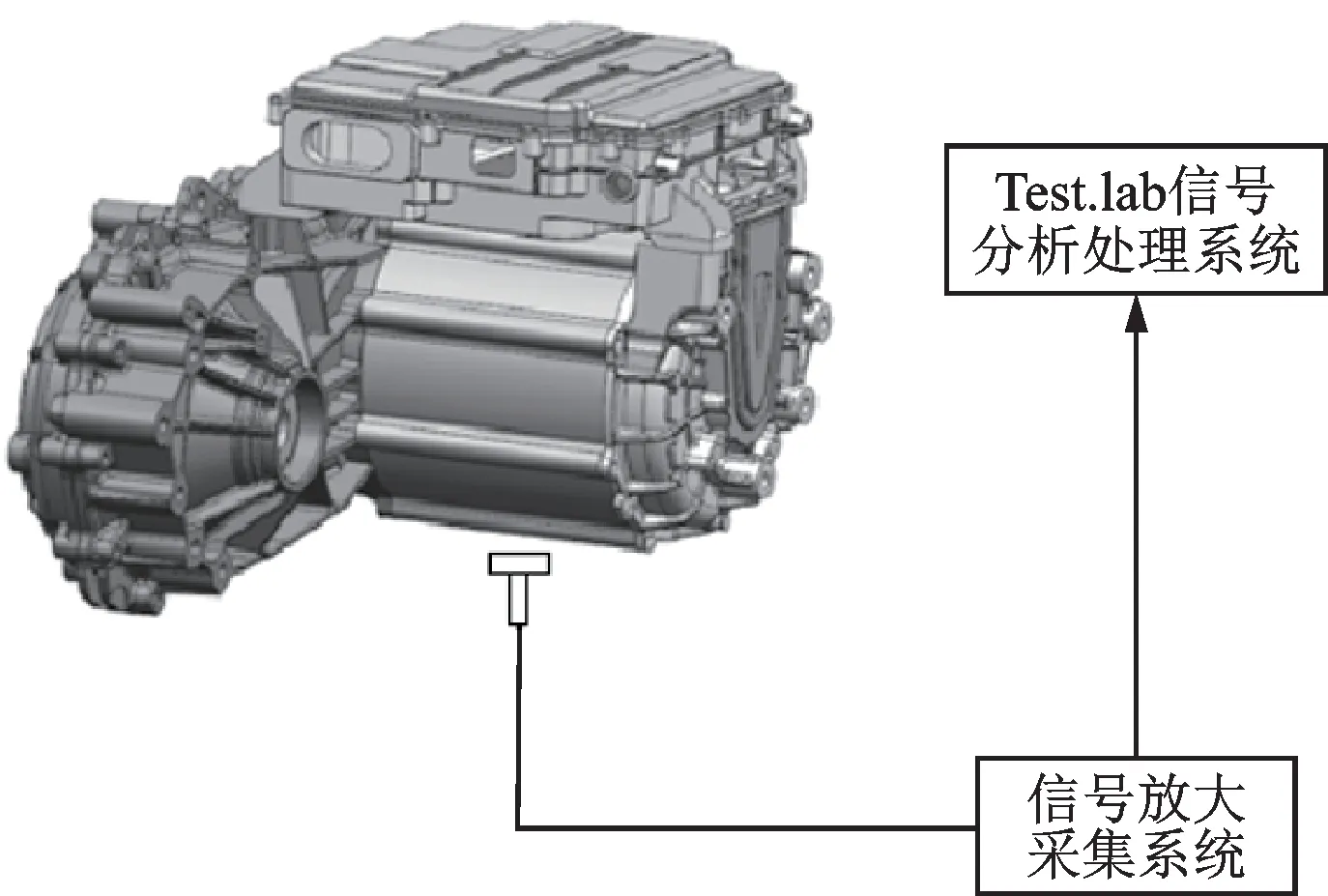
图7 动力总成振动测试示意图Fig.7 Diagram of powertrain vibration test system

图8 测点位置图Fig.8 Location of measuring points

从图9可以看出，动力总成在低速时振动幅值较大，尤其在500～1500 r/min 区间内出现了两个大的峰值。为了进一步确认引起振动的原因，在上述台架上继续对动力总成进行工作振型（ODS）测试，即在电机、减速器以及控制器表面均匀布置一系列加速度传感器，测试结构表面的位移响应，并通过Test.lab信号分析处理系统得到其工作振型如图10所示。

图9 48 阶振动测试结果Fig.9 Test result of 48-order vibration

图10显示了动力总成在1300 r/min 处不同时刻的工作振型。通过两个振型图的变化可以判断，电机、减速器整体呈现明显扭动状态，根据文献［16-17］，认为扭转振动与转矩脉动呈线性相关，特别是低速时转矩较大，转矩脉动对动力总成的冲击激励大，易导致其扭转振动。根据上述分析结果，认为48 阶低速区振动噪声问题是转矩波动激发总成弯扭模态引起的。

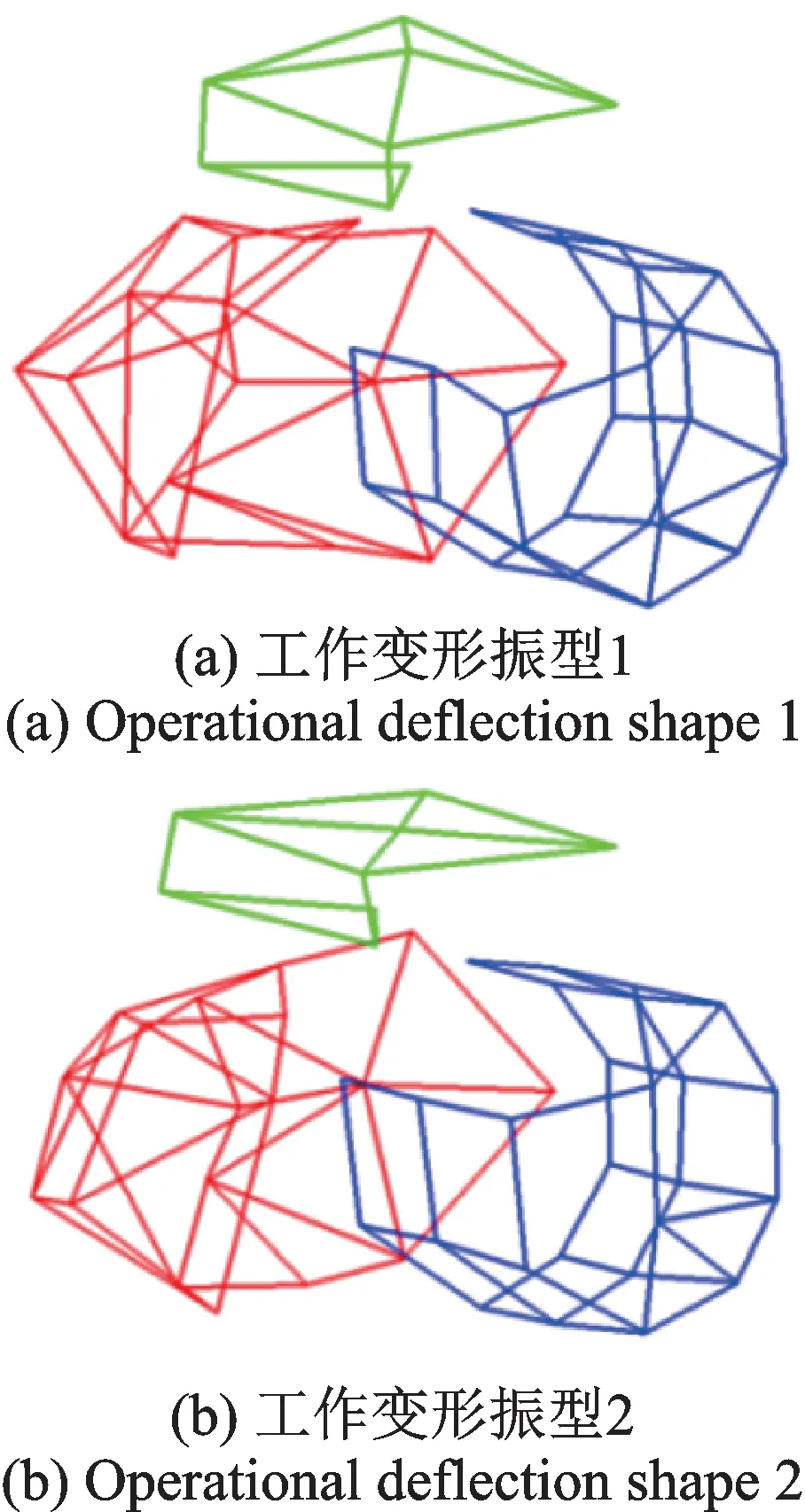
图10 动力总成工作变形振型图Fig.10 Operational deflection shape of powertrain

3 动力总成电磁振动优化研究

3.1 基于谐波注入的转矩脉动抑制方法

为了抑制动力总成的扭转振动，本文以转矩脉动最小化为目标，通过注入谐波电流以产生额外的谐波转矩分量来抵消原有的转矩脉动，具体算法如图11所示。在d，q轴电流回路中增加以幅值和相位为参数的、与转矩脉动相同阶次的谐波电流，本文主要为抑制48 阶转矩脉动，即电频率的12 倍。

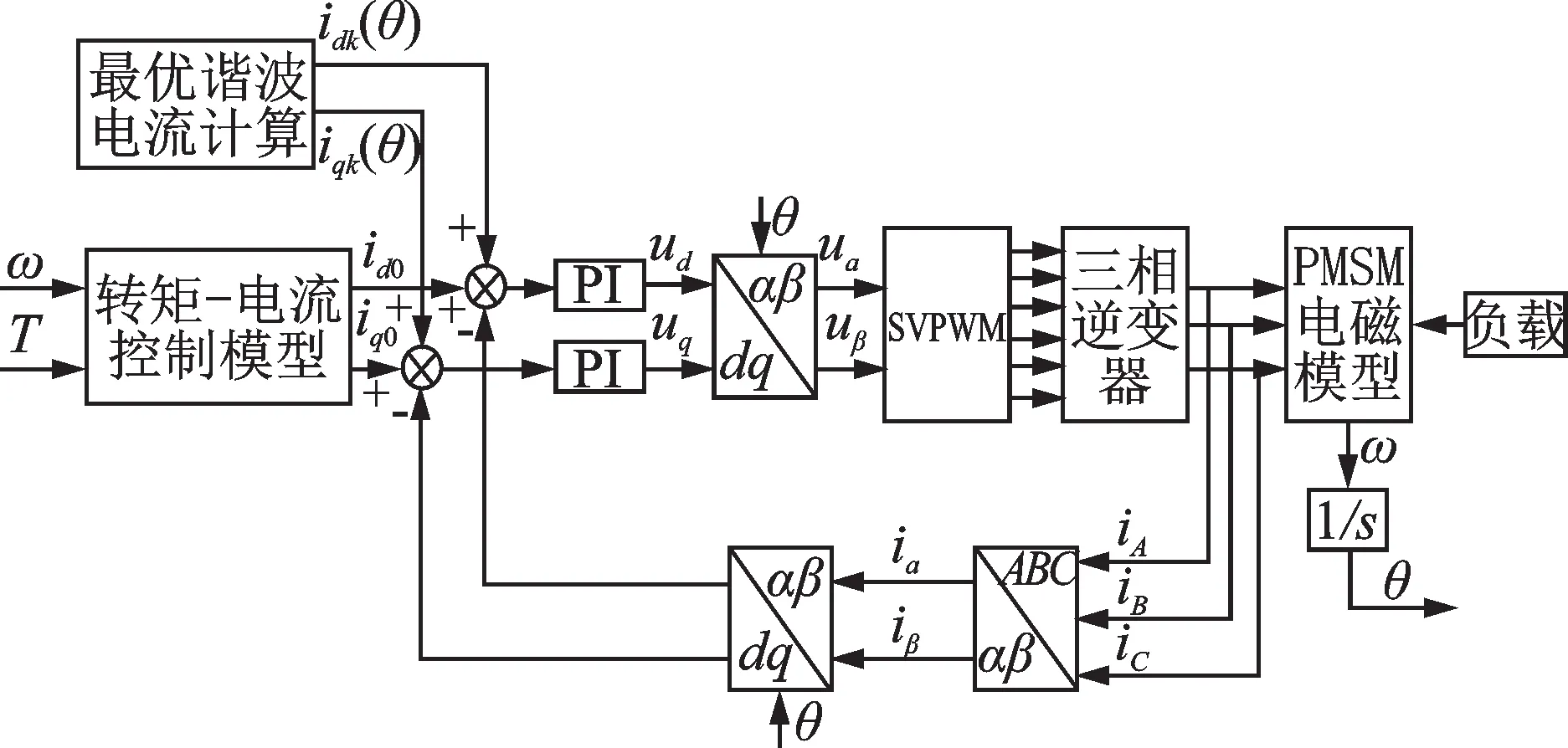
图11 基于谐波注入的转矩脉动抑制算法Fig.11 Torque ripple suppression algorithm based onharmonic injection

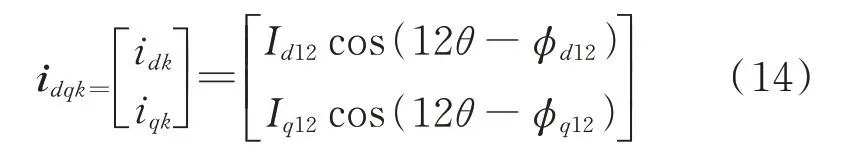
式中Id12，Iq12，ϕd12，ϕq12分别为d，q轴对应谐波电流的幅值和相位参数。

3.2 谐波电流优化

本文采用径向基函数（RBF）神经网络代理模型和遗传算法结合的方法来优化电流参数，流程图如图12所示。通过合适的样本点对神经网络进行训练，从而得到精度较高的代理模型，然后基于代理模型采用遗传算法对谐波电流进行优化。

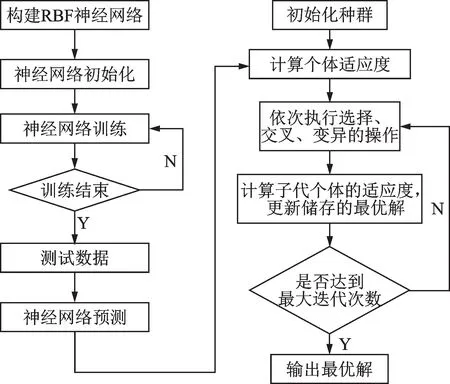
图12 RBF 神经网络和遗传算法寻优流程图Fig.12 Flow chart of RBF neural network and genetic algorithm optimization

样本点的选取采用拉丁超立方抽样方法，随机获取电流参数Id12，Iq12和相位ϕd12，ϕq12。通过上述联合仿真获得2000 个样本点的平均转矩和转矩脉动值，转矩脉动可以用输出转矩的峰峰值与平均值的比值计算得出，如下式所示：

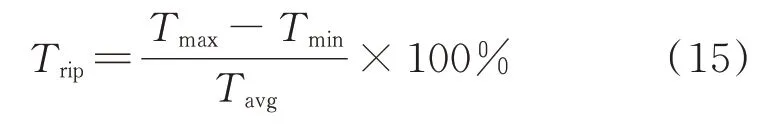
式中Trip，Tavg，Tmax，Tmin分别表示电机的转矩脉动、输出平均转矩、输出的转矩最大值和最小值。

采用1900 个样本作为训练样本，经过神经网络训练后，将剩余100 个样本作为输入代入神经网络中，以验证代理模型的准确性。联合仿真与神经网络代理模型拟合结果比较分析如图13所示。从图中可以看出，虽然一些样本点结果存在误差，但是误差都在3%以内，且激活函数的决定系数R2超过0.99，因此认为该代理模型预测精度高、泛化能力强，可以为后续的优化提供良好的基础。

图13 有限元与神经网络拟合结果的比较Fig.13 Comparison of finite element and neural network fitting

本文以谐波电流的幅值Id12，Iq12和相位ϕd12，ϕq12为优化变量，选择平均转矩作为约束条件，转矩脉动作为优化目标，遗传算法优化电流谐波的数学模型为：

首先遗传算法随机产生一个初始种群，然后调用训练好的RBF 神经网络模型计算群体中的个体适应度，电流参数为神经网络模型的输入，平均转矩和转矩脉动是神经网络的输出，将平均转矩作为限制条件，转矩脉动作为遗传算法的适应度函数；然后根据个体适应度进行选择、交叉和变异操作，使适应度好的个体被保留，适应度差的个体被淘汰，不断循环直到满足遗传算法的终止条件，从而得到谐波电流的最优值。

4 优化效果分析

4.1 转矩脉动优化效果分析

通过上述遗传算法找到抑制转矩脉动的最优电流，并在联合仿真中对其进行精确闭环控制，得到优化前后电磁转矩波形对比图及优化后的转矩频谱图，如图14和15 所示。从图中可以看到，在谐波注入之后，电磁转矩曲线变得平缓，且从频谱图可以得知，48 阶转矩谐波抑制效果明显，转矩从3.825 N·m降至0.4397 N·m。

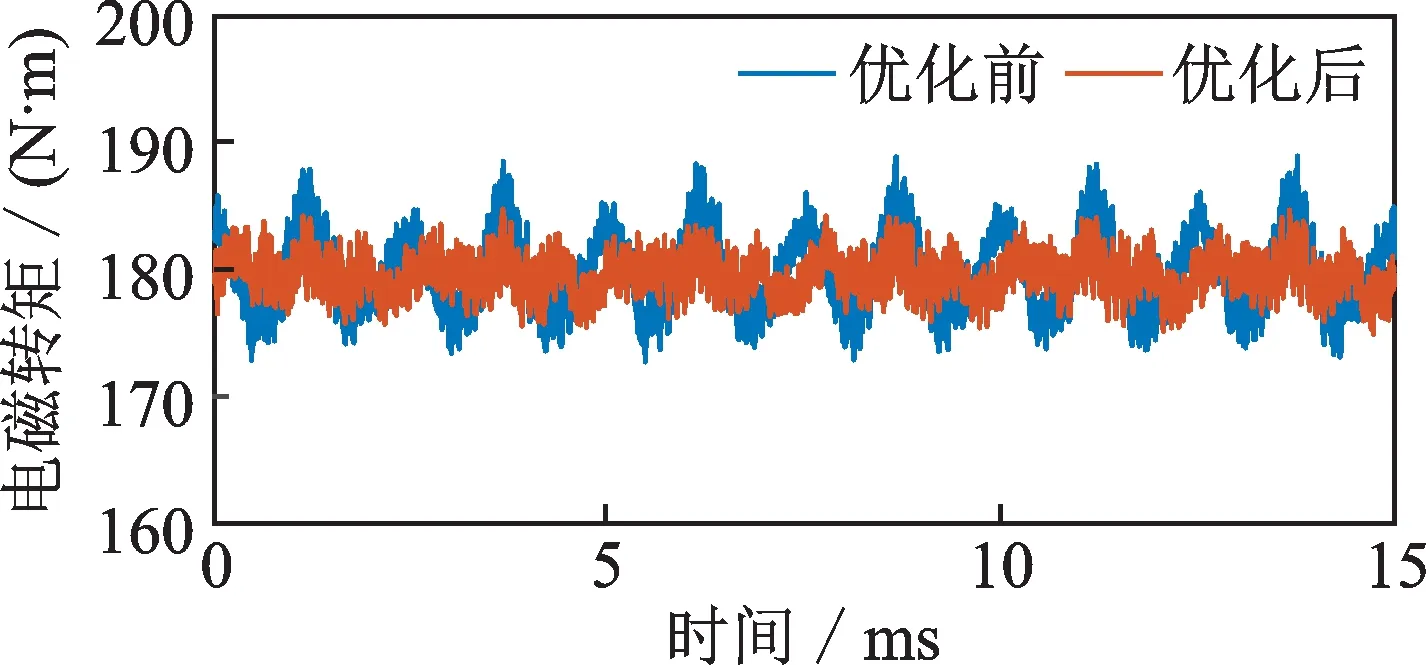
图14 优化前后电磁转矩波形对比Fig.14 Waveforms of electromagnetic torque before and after optimization

图15 优化后的转矩频谱图Fig.15 The spectrum of optimized torque

4.2 总成电磁振动优化效果实验验证

结合动力总成台架试验，利用振动测试设备验证谐波电流注入前后的电驱动系统48 阶振动的差异，如图16所示。试验结果表明，谐波注入后动力总成在500～2000 r/min 区间内48 阶振动抑制效果显著，一方面说明在该转速段内转矩脉动为主要激励源，另一方面也验证了本文方法的可行性。实验结果显示，动力总成在全油门工况下表面振动加速度最高下降15 dB，显著提高了电驱动系统的NVH品质。

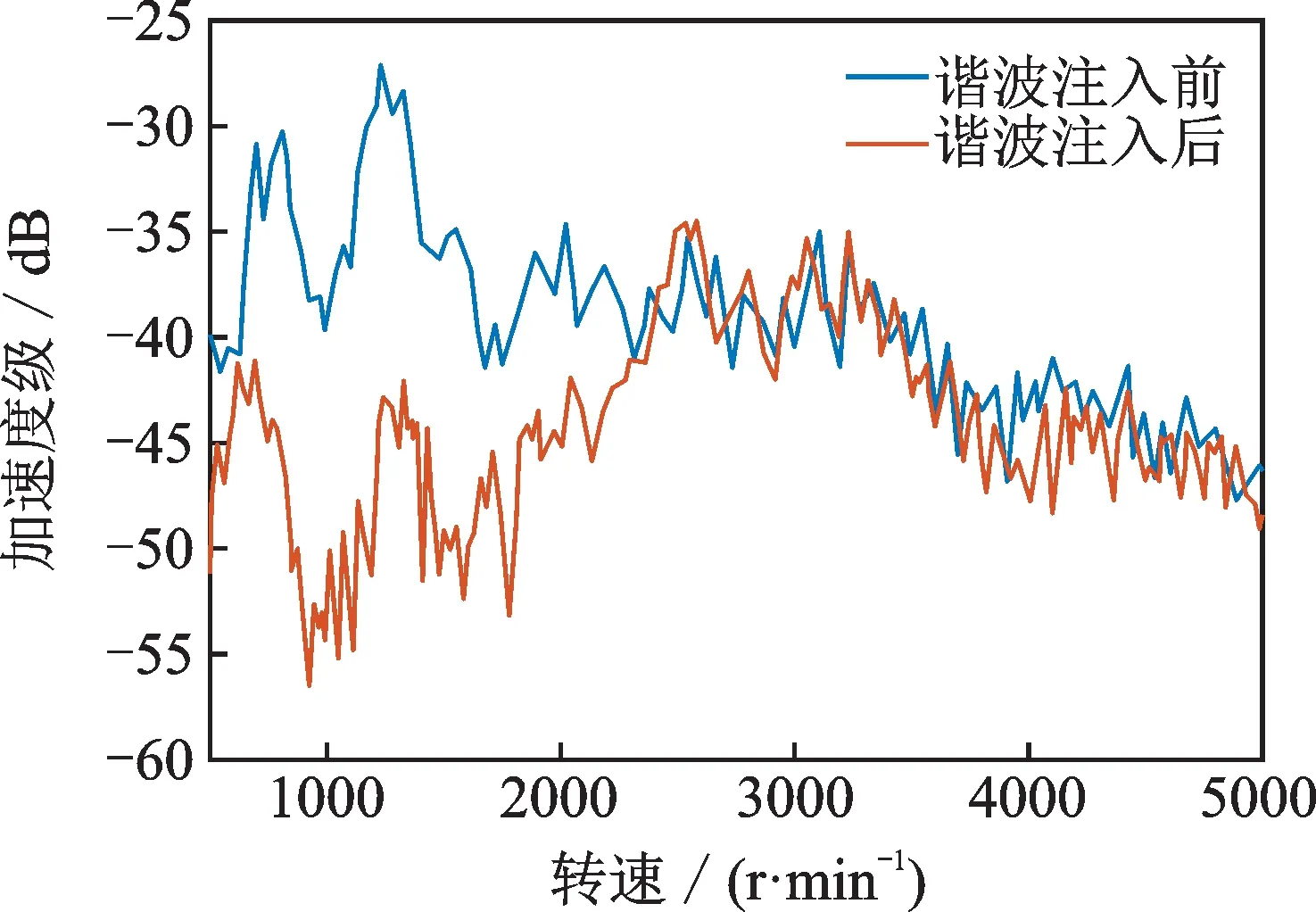
图16 谐波注入前后的振动测试结果Fig.16 Vibration test results before and after harmonic wave injection

5 结 论

本文首先分析了转矩脉动的数学模型和谐波注入的原理，建立某8 极48 槽内置式永磁同步电机联合仿真模型，得到空间矢量脉宽调制下动力总成的电磁激励特征。针对转矩脉动引起的扭转振动问题，采用谐波电流注入的方法来抑制48 阶转矩脉动，通过台架振动试验，证明了谐波注入方法对电磁振动抑制的可行性。得到的主要结论如下：

1）对于集中式动力总成，转矩脉动对总成的振动影响较大，尤其是会使电机和减速器之间产生相对扭转运动，且主要集中在低转速区域。

2）采用谐波注入方法来抑制转矩脉动，对改善动力总成低速区的电磁振动具有较明显的效果。由于受开关频率的限制，转速较高时谐波电流会出现采样失真，因此，基于谐波电流注入的方法适用于低速应用场合。