Smagorinsky常数对扁平箱梁气动特性大涡模拟的影响研究

祝志文，刘帅永，刘震卿

（1.汕头大学土木与环境工程系，广东 汕头 515063；2.华中科技大学土木工程与力学学院，湖北 武汉 430074）

引 言

扁平钢箱梁不仅承载力大、结构轻，而且因结构高度小，导致风荷载小，是大跨度桥梁常用的主梁结构形式，如广州南沙大桥、丹麦大带东桥、润扬大桥和江阴大桥等均采用扁平钢箱梁。在大跨度桥梁抗风中，扁平箱梁气动特性的获得目前主要通过节段模型风洞试验，但风洞试验涉及模型制作，试验周期长、费用高，且模型缩尺比往往较小，使得风洞试验的雷诺数往往远低于实际桥梁绕流Re数。计算流体力学（CFD）基于计算机和数值方法求解流体动力学问题，在风工程研究中应用广泛。随着计算机特别是并行计算的发展，CFD 有望为风工程研究提供一种可能代替风洞试验的手段。与风洞试验相比，CFD 模拟无需模型制作和测量设备，能回避或解决风洞试验中存在的诸多问题，且能形象而又细致地再现风的复杂流动，能借助其强大的后处理和流场可视化开展微观分析，便于揭示流动机理。另外，CFD 模拟能够生成满足指定风场特性的入口来流，方便修改流场参数，可不受测力和测压模型限制获得气动力，能够灵活布置大量表面压力采集点，也无采集管路系统频响特性对风压信号动态特性的影响。

与湍流模拟的其他CFD 方法相比，LES 采用过滤方法将流场变量分解成大尺度脉动和亚格子脉动两部分，直接计算大尺度的脉动，亚格子脉动通过湍流模型模拟，其对流动的非定常特性有较高的捕捉能力。LES 最早由Smagorinsky［1］于1963年提出，随着计算能力及数值方法的不断改进，LES 在20世纪90年代后获得了巨大发展，广泛应用于复杂流动的模拟中，桥梁风工程方面的相关研究文献也越来越多。

作为一种经验湍流模型，LES 目前存在的问题是Smagorinsky 常数CS的不确定：CS的取值并非定值，可能与流场类型、雷诺数及其他无量纲参数相关［2］。为此，学者对CS的合理取值进行了广泛研究。对于截断波数处于惯性子区范围且过滤尺度与网格尺寸相等的均匀各向同性湍流，Lilly［3］基于能谱分析得到的CS取值为0.23。Deardorff［4］在槽道湍流的模拟中发现采用文献［3］建议的CS值会导致亚格子应力黏性过大，而当CS取0.1 时，模拟结果与Laufer［5］试验相近。Kwak 等［6］、Shaanan 等［7］、Ferziger 等［8］和Antonopoulos-Domis［9］基于Smagorinsky模式得到了与Comte-Benot 和Corrsin［10］试验一致的能量衰减率，其CS取值范围为0.19～0.24。Mason和Callen［11］研究认为CS取值与网格分辨率有关，当网格分辨率足够高时，CS取0.2 能给出较好的结果，反之，如网格分辨率不高，CS的取值须小于0.2。Piomelli 等［12］研究表明即使网格分辨率比Mason 等［11］所使用网格高得多，CS的最佳取值仍为0.1 左右。Germano 等［13］提出了一种动态亚格子模型，将C2S作为时间和空间的函数，用不同特征长度的两个滤波函数来确定。可见目前还没有解决CS的合理取值问题，而现有桥梁主梁LES 采用CS=0.1［14］，其合理性也是存疑的，因为绕扁平箱梁的流动，与自由剪切流和槽道湍流差别较大，包含钝体绕流的分离、冲撞、自由剪切层和旋涡脱落等各种不同的流动结构。

因此，研究LES 参数CS的合理取值，并提出相应建议，对采用LES 获得扁平闭口箱梁的气动特性有重要的工程意义，但目前无相关研究报道。

1 LES 的基本原理和控制方程

LES 的基本思想是，湍流由不同尺度的漩涡组成，大尺度的涡旋对湍流能量和雷诺应力的产生及流动量的扩散起主要作用。大涡的行为强烈依赖于边界条件，随流动的类型而异。小涡的上述贡献较小，最小尺度的涡主要起耗散作用。高雷诺数下小涡近似于各向同性，受边界条件影响较小，具有较大的共性［15］。虽然目前的计算机还不能计算到耗散尺度，但能够小到惯性区尺度，所以可通过离散非定常Navier-Stokes（N-S）方程来确定大涡的行为，而用较通用的模型模拟小涡的作用。

LES 将N-S 方程中流场速度变量ui变成大尺度可直接求解的变量，加上过滤掉的亚格子尺度量u′i，即：

式中第一项表示大于过滤尺度的大涡量，是在整个计算域D上通过下述卷积积分获得：

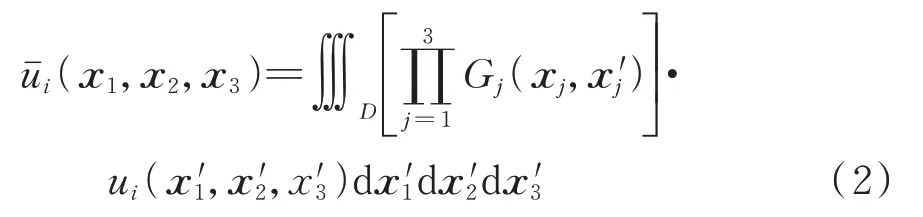
式中xj和x′j均为空间坐标向量；Gj为过滤函数，并满足：

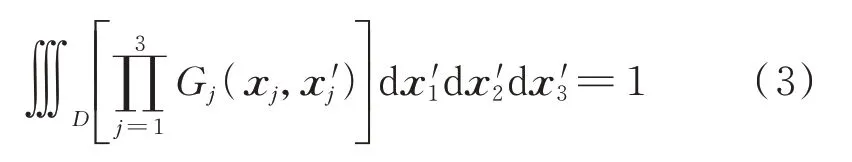
在有限差分法和有限体积法空间离散中，最常采用的是体积加权的盒函数过滤器，即：

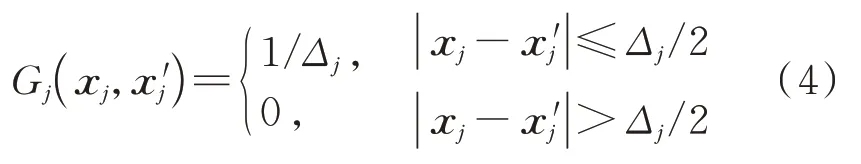
式中Δj(j=1，2，3)为坐标轴方向的网格尺度，过滤得到的不可压N-S 方程形式为：

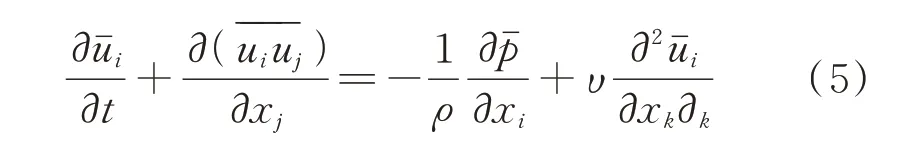
式中ρ和υ分别为空气密度和运动黏性；为过滤后的压力。因无法同时求解和，需要将作分解，也即τij为亚网格剪应力张量，τij=为亚格子湍流黏性；δij为狄拉克函数；Sˉij为根据求解的大涡量确定的应变率张量，可表示为：

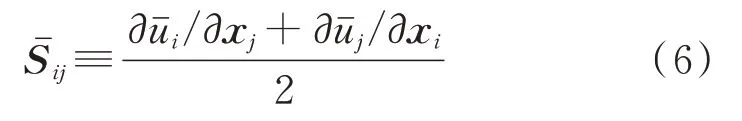
这样，包含连续方程在内的不可压N-S 方程可表示为：

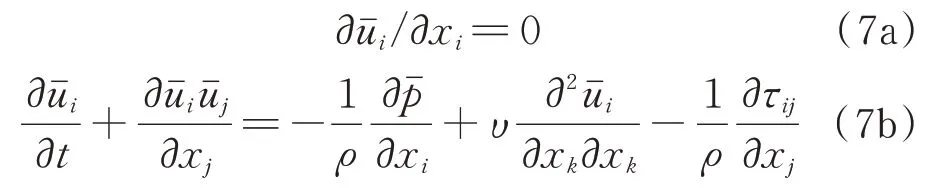
对LES 常采用的Smagorinsky 模型［3］，则亚格子湍流黏性可表示为：

与雷诺数均等时其他湍流模型需要多个经验化的模型参数相比，LES 仅需一个经验参数CS，因此，LES 的模型参数数量显著减小。另外，从式（8）可见，当CS增加时，亚格子湍流黏性将增大，此时流动的耗散作用将增强，将导致非定常流动中亚格子尺度小涡的作用减弱，改变湍流中不同尺度涡之间能量级联方式，降低LES 对流动非定常特性的捕捉能力，比如导致气动力的脉动量减小、流动频谱中高频分量的衰减或缺失、频谱变窄，也可能会改变漩涡脱落特性。此外，对流场的细部结构，如主梁表面的流动分离、再附、剪切层运动和复杂尾迹流动均可能产生影响。

本文LES 基于Fluent 6.3.26 软件，以大带东桥主梁为对象［16］，根据LES 获得的气动特性与试验结果的对比，探讨扁平箱梁气动特性LES 在CS上的合理取值。

2 数值方法和边界条件

合理的CS取值需对比LES 结果与风洞试验结果。本文以大带东桥主跨加劲梁标准断面施工阶段为对象，不考虑桥面防撞栏等附属设施。实桥主梁全宽31 m，高4.4 m，主梁扭转中心（S.C.）位于桥轴线主梁底板以上2.35 m 处。CFD 模型缩尺比为1∶80，对应的模型截面宽B=0.3875 m，高D=0.055 m，顺桥向模型长度取一倍模型截面宽度，也即L=B，主梁CFD 横截面如图1所示。

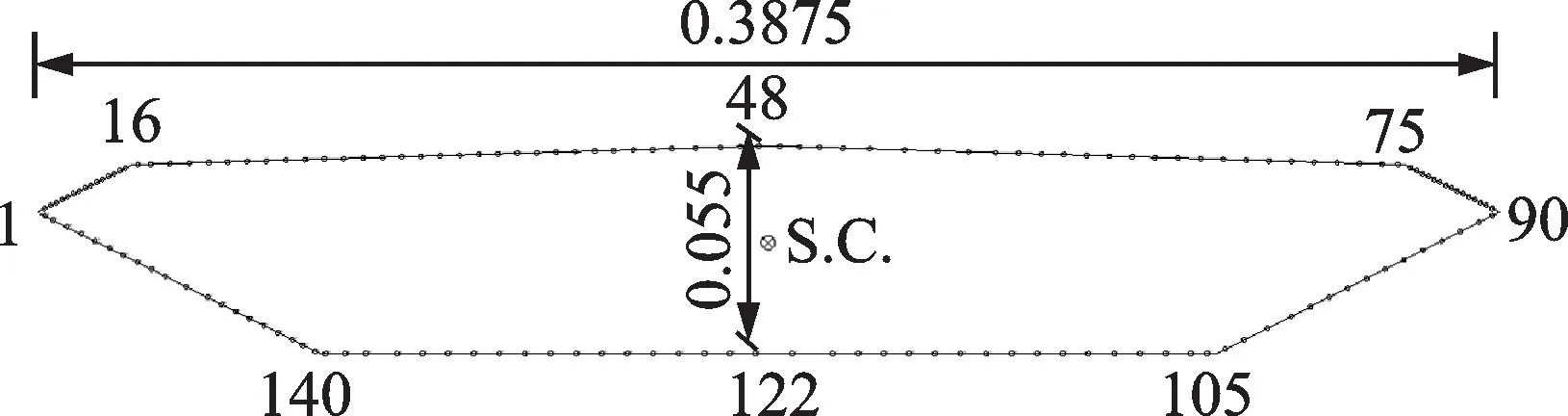
图1 CFD 主梁横断面尺寸和表面监测点布置（单位：m）Fig.1 Girder cross section and surface monitoring points in CFD（Unit：m）

图2（a）为计算域和主梁网格布置示意图，其中入口、上下侧边界到主梁S.C.点的距离均为10B，下游出口到S.C.点的距离为20B，计算域展向长度等于模型长度L。模型在计算域内的堵塞度为0.7%，远低于3%的CFD 模型堵塞度要求。

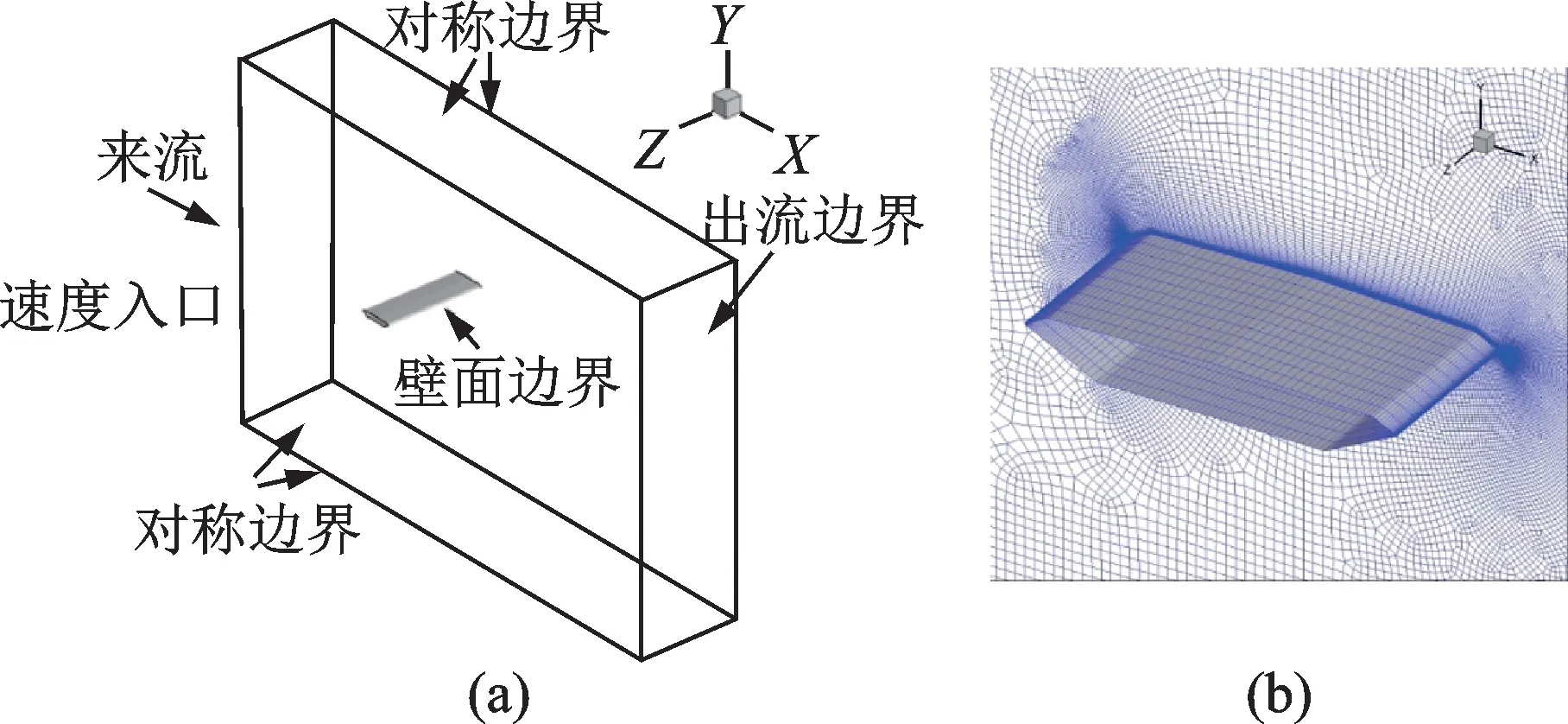
图2 计算域和网格布置Fig.2 Computational domain and mesh arrangement

采用结构和非结构六面体网格控制计算域网格数量和质量，并控制同一网格方向相邻网格的高度比不大于1.1，在流动变量变化梯度大的风嘴前缘和主梁表面折角附近加密网格，在物面法向采用精细的结构化六面体网格划分，并保证网格的正交性，提高模型尾流区网格分辨率。在流动变量变化平缓的区域采用较粗的网格，以降低网格总量。

来流风速U0= 5 m/s，风攻角为0°。计算域边界条件，在入口设置为均匀流速度边界；下游出口施加出流边界；主梁表面采用无滑移壁面条件；计算域的顶面和底面，以及模型展向两侧面均设为对称边界，如图2（a）所示。计算域初始场采用入口速度条件初始化。开展了LES 模拟的网格无关性和时间步无关性检查，因篇幅限制，本文不再列出。综合比较计算量和模拟精度要求，确定模型表面法向第一层网格高度为B/1300，时间步长为0.0002 s，模型表面Y+满足LES<1 的要求。计算域网格总数为986544，对应的流动雷诺数为1.33×105。

3 CS取0.1 时主梁的气动特性

CFD 计算在模型表面布设了160 个压力监测点，以捕捉不同时刻模型表面的压力分布，如图1所示。定义监测点的压力系数CP为：

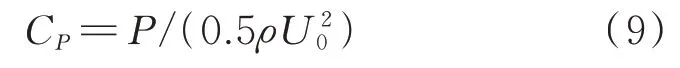
式中P为监测点压力；CP的平均值和RMS 值分别加下标m 和RMS 表示。

定义气动力作用点在图1截面的S.C.点，分别定义模型断面气动阻力、升力和扭矩系数为：

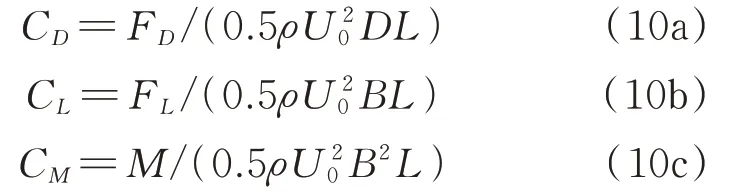
式中FD，FL和M分别为作用在主梁上的阻力（顺来流方向为正）、升力（垂直来流方向向上为正）和扭矩（顺时针方向为正）；三分力系数的平均值和脉动RMS 值分别再加下标m 和RMS 表示。

定义主梁漩涡脱落St数：

式中fs为主梁漩涡脱落频率（Hz）。

以后缘压力监测点90为参考，图3给出了扁平箱梁紧靠6个棱角的压力系数时程曲线。可见这些时程曲线均表现出频率相同但幅值不同的波动。除迎风侧上斜腹板监测点1风压系数为正外，其他均为负；下表面风压脉动明显大于上表面，最大风压脉动出现在迎风侧下斜腹板与底板相交处，其次是迎风侧下斜腹板紧靠前缘的点。另外，从时程峰值对比来看，监测点压力并不同步，部分同相、部分反相。

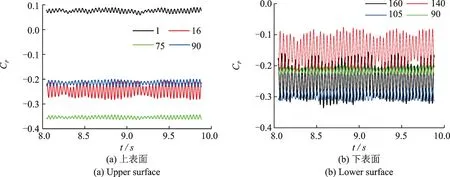
图3 主梁表面典型监测点风压系数时程Fig.3 Pressure coefficient time histories at typical monitoring points on girder surface

图4（a）为气动三分力系数时程。可见阻力系数时程呈现随机波动特性，阻力时程对应的平均阻力系数为0.435，比基于刚性模型测压积分获得的阻力系数0.352 高18%［16］；LES 捕捉到了较大的升力系数波动，呈现出规律的波动特征，隐含绕流明显的涡脱特征。图4（b）升力时程的功率谱密度（PSD）分析表明，显著峰值占优的频率对应的St数为0.29，也即为单一频率涡脱，这与风洞试验结果完全吻合［16］。

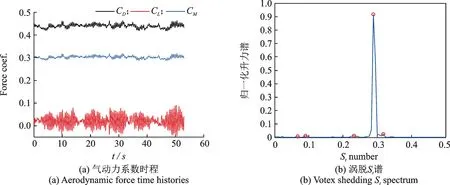
图4 气动力系数时程和涡脱St谱Fig.4 Aerodynamic coefficients time histories and vortex-shedding spectrum

图5为从升力时程峰值时刻开始，在一个涡脱周期T内主梁周围压力云图。模型后缘上下表面出现明显的交替脱落的漩涡，从而在主梁表面诱导出波动的气动力，如图4（a）所示。国内外多座大跨度扁平钢箱主梁桥梁出现了涡激振动，图5的流动可视化有助于理解扁平箱梁涡脱产生的流动机理。

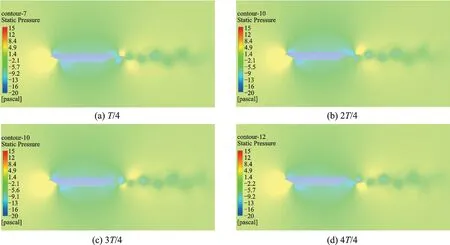
图5 一个涡脱周期T 内的压力云图Fig.5 Pressure contours around girder in one vortex-shedding cycle

4 不同CS值对主梁气动特性的影响

开展了CS在0.032～0.70 范围取值以及动态亚格子黏性模型的多个LES 计算，其他计算设置和条件均与上节相同。CS值从0.032 开始逐渐增大，为提高计算效率，后一个CS值计算工况在前一个CS值收敛结果上开展，由于CS值前后差别很小，前一次CS值计算的收敛结果是后一个CS值计算工况的良好初始场。每个CS值计算工况，在计算残差收敛平稳后，再计算65 个涡脱周期［17］，得到1.3×104个时间步上的主梁气动力时程和监测点风压时程。

不同CS取值时LES 得到的主梁气动力平均值和RMS 值如图6所示。可见力系数平均值变化不明显，阻力系数随CS值的增大先有小幅增大，随后小幅减小，最大变化量不大于10%；升力系数平均值也是先小幅增大再减小，最大差值约0.05。力系数RMS 值随CS值的增大均呈现减小的趋势，特别是升力系数RMS 值最显著；当CS值大于0.50 后，力系数RMS 值为零，也即其时程将为一条水平直线。这说明，随着CS值的增大，亚格子湍流黏性增大，此时流动的耗散作用增强，使得LES 对主梁绕流非定常特性的捕捉能力降低，导致气动力脉动减小。

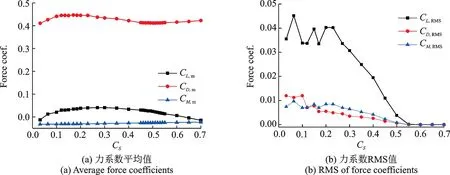
图6 主梁力系数平均值和RMS 值随CS的变化Fig.6 Mean and RMS values of aerodynamic coefficients of girder under various CS values

为探讨CS取值对主梁漩涡脱落的影响，本文对不同CS取值获得的升力时程，开展了PSD 分析，并将横轴换算为涡脱St数，可得到相应CS取值工况下的主梁涡脱St谱。为区分主梁涡脱的单频（频谱只有一个峰值）和多频（频谱有多个明显的峰值）特征，涡脱St谱也需反映单频和多频特征（风洞试验St=0.28～0.29，为单频［16］），本文对涡脱多频的情况给出了前2 个峰值对应的St数。图7给出了主梁涡脱St数随CS值增大的变化，结合图4（b），可见当0.064≤CS≤0.45，主梁涡脱均呈单峰特征，且涡脱频率随CS增大而小幅减小。图8另外给出了多个CS值下的涡脱St谱，可见在上述范围之外，主梁涡脱呈现多峰特征；参考试验结果［16］，可见在0.064≤CS≤0.27 范围内，LES 均能给出主梁涡脱St数的合理估计。另外，采用动态亚格子黏性模型，LES 无法给出主梁涡脱的合理估计，如图8（d）所示，这与Ferziger 等［18］的结论一致。

图7 主梁涡脱St数随CS值的变化Fig.7 Girder vortex-shedding St versus various CS

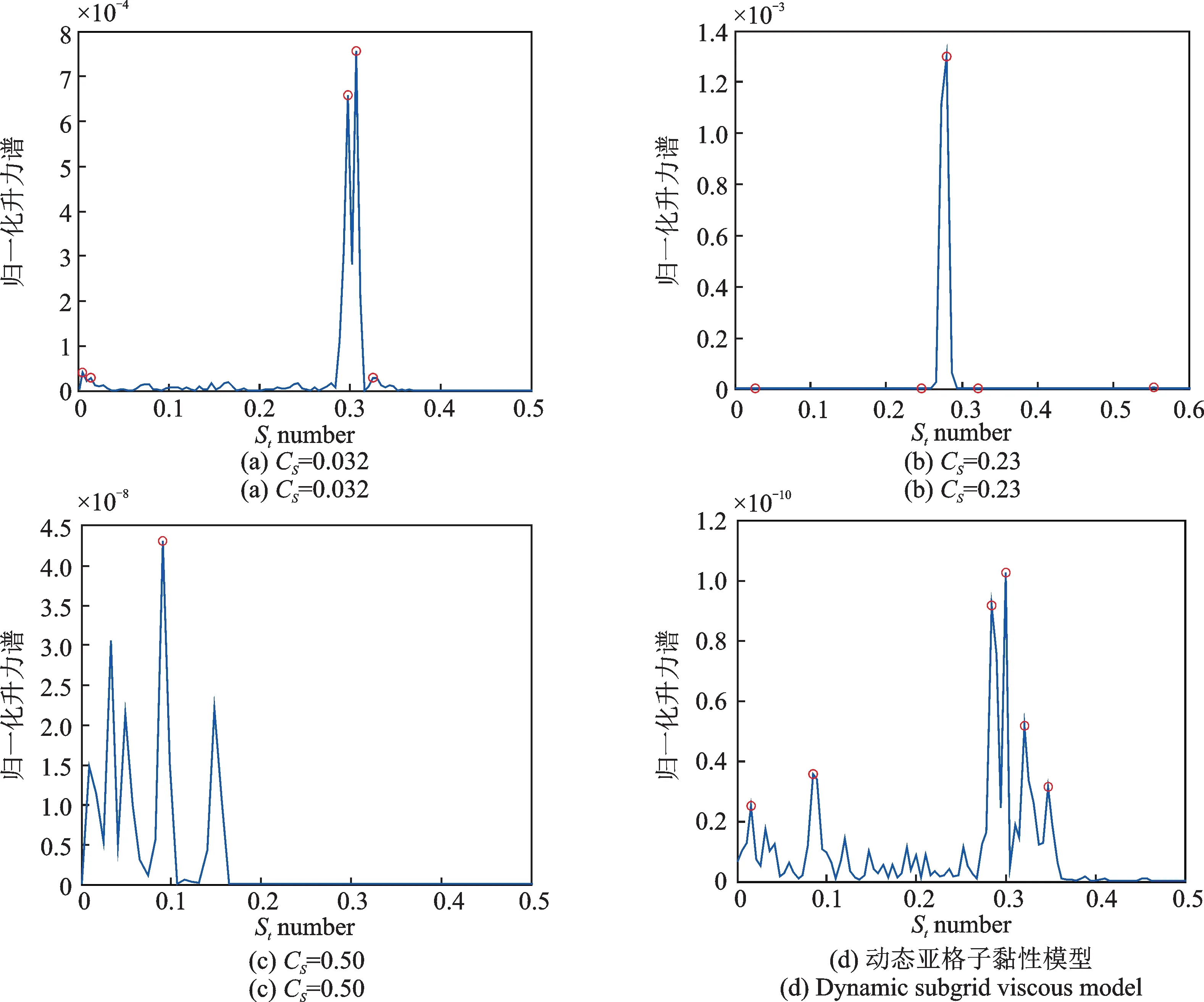
图8 不同CS值主梁涡脱St谱Fig.8 Girder vortex-shedding St spectrum under various CS

从图7的涡脱St谱特征考虑，开展了0.032≤CS≤0.50 和动态亚格子黏性模型的LES 计算，将主梁表面压力系数平均值和RMS 值与风洞实验进行了对比。由图9和10 可见，对全部CS值，表面压力系数平均值与风洞试验结果，除在靠近前缘附近2个监测点外，其他吻合良好。在顶底板迎风侧折角位置处，LES 给出了比试验更大的极值负压估计，这可能与CFD 布置的监测点更靠近折角有关。实际上，因风洞模型制作困难，测压管无法像CFD 一样能紧靠模型折角。

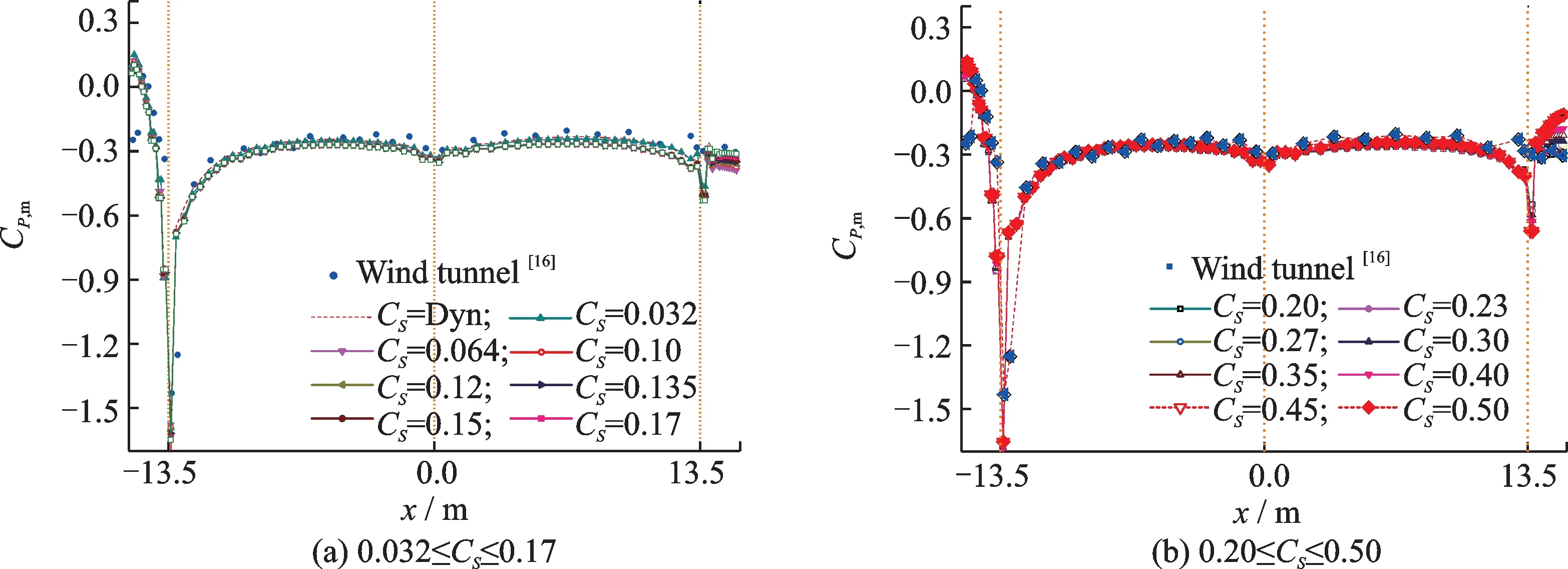
图9 主梁上表面压力系数平均值Fig.9 Mean pressure coefficients on girder upper surface

图11和12 为0.032≤CS≤0.50 和动态亚格子黏性模型下，LES 获得的主梁表面压力系数RMS 值与风洞实验的对比。可见对全部CS值，压力系数RMS 值均与风洞试验结果存在差异，表现为LES低估了压力脉动值，特别是在主梁的中后部，后缘附近的差别较大。上述结果与风洞试验的差别，还随着CS值的增大而进一步增大。动态亚格子黏性模型能得到较大的压力系数RMS 值，但也未能获得与试验结果相一致的趋势。显然，CS值的增大不利于LES 捕捉流场的脉动量。

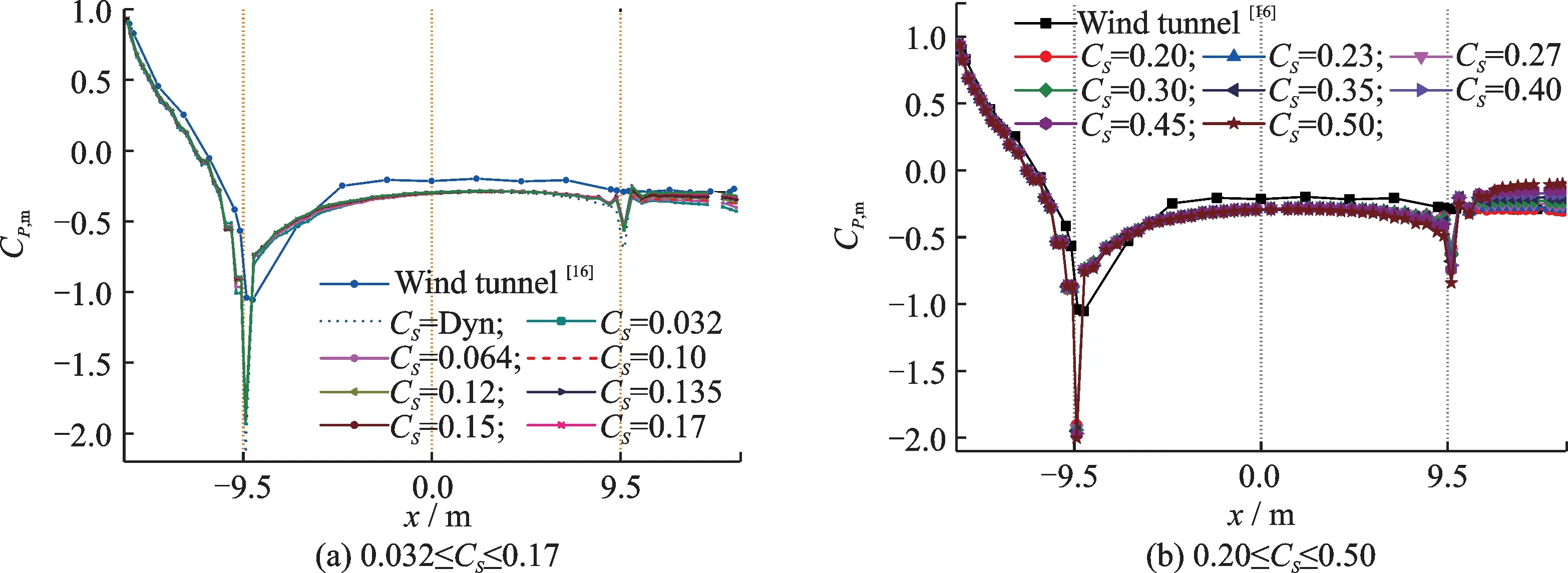
图10 主梁下表面压力系数平均值Fig.10 Mean pressure coefficients on girder lower surface

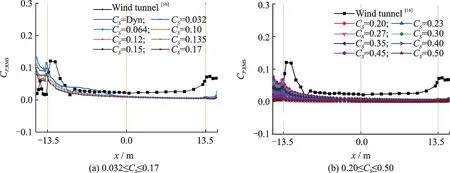
图11 主梁上表面压力系数RMS 值Fig.11 RMS pressure coefficients on girder top surface

5 结 论

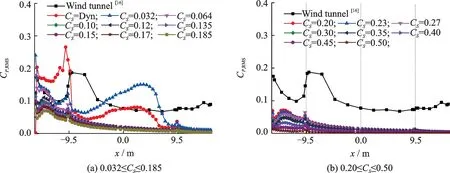
图12 主梁下表面压力系数RMS 值Fig.12 RMS pressure coefficients on girder bottom surface

本文开展了CS在0.032～0.70 范围以及动态亚格子黏性模型的LES 多工况模拟，获得了主梁气动力、漩涡脱落St数、表面压力系数平均值和RMS 值，并与风洞试验结果进行了对比，基于数据分析和讨论，得到下述结论：

1）CS取0.1，LES 能捕捉到主梁气动力和漩涡脱落的非定常特征，估计的St数与风洞试验吻合。

2）CS值对主梁表面压力系数和气动力系数的平均值影响均不明显，且其结果与风洞试验吻合良好；CS值对压力系数和气动力系数的RMS 值影响明显。随着CS增大，亚格子湍流黏性增大，流动的耗散作用增强，使得LES 对流动的非定常特性捕捉能力降低，导致气动力的脉动量减小。当CS值大于0.5 后，气动力将不再出现脉动。

3）在顶底板前缘折角位置处，LES 给出了比试验更大的平均负压极值估计。压力系数的RMS 值和分布均与风洞试验结果存在差异，且差异随CS值的增大而增大。动态亚格子黏性模型能给出较大的压力系数RMS 值和与风洞试验不同的分布，也无法给出主梁涡脱的合理估计，不建议采用。

4）在0.064≤CS≤0.27 范围内，LES 均能给出与风洞试验一致的主梁涡脱单频St值估计，从捕捉流动的非定常特性考虑，建议CS在上述范围内取小值。

另外，LES 获得的压力系数RMS 值和分布均与风洞试验结果存在差异，是否与LES 计算域入口来流条件有关，值得进一步研究。