关于随机和概率分布律递推公式的探讨

徐 怀，赵钰萱，蒋书涵， 陈 丹

(安徽大学 1.数学科学学院；2.纽约石溪学院；3.大数据与统计学院；4.管理学院, 合肥 230039)

1. 前言

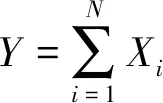
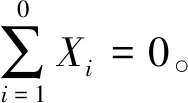
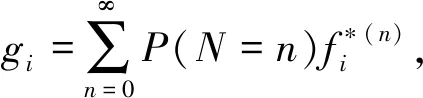
2. 递推公式及其证明

在这一节中，我们证明随机和概率分布率的递推公式。

首先指出下述两条显然的性质：

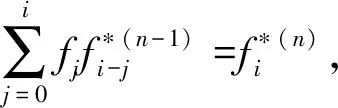
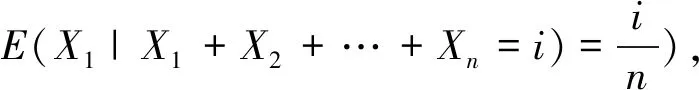
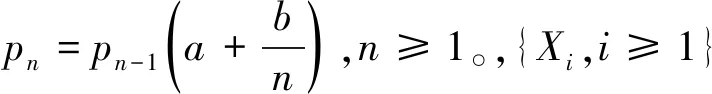
证明：

关于g0的证明是一目了然的，我们略过。

下证gi,i≥1

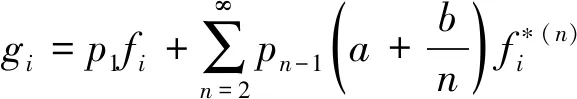
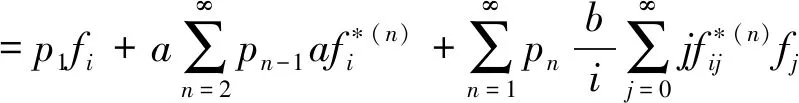
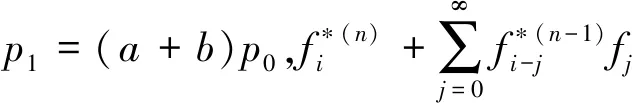
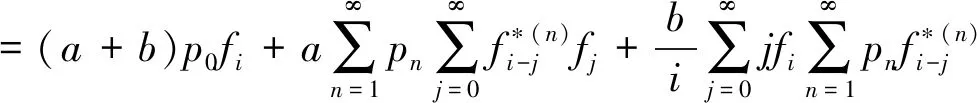
分解上式中的第二和第三项得，

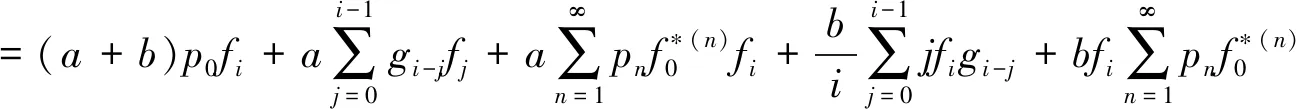
分解第一项，分别于第三项和第五项合并得，

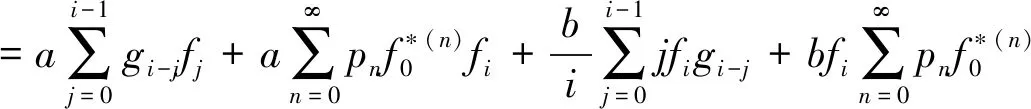
分别合并第一和第三项，第二和第四项得，

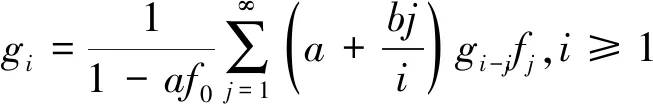
3. 算法步骤

根据上述的递推公式，设计以下的算法过程：

步骤1 根据随机变量NXi对a,b,fi变量赋初值

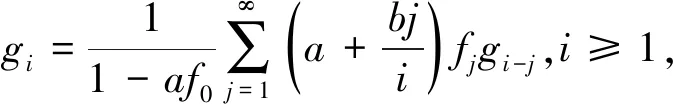
步骤3 对随机和的概率分布律gi求和，判断∑gi是否等于1，若小于1，重复步骤2。若等于1，进入步骤4。

步骤4 输出概率分布列和概率分布列，绘出图形。

4. 数值例子

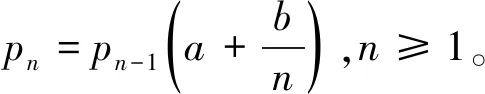
(1)计数的随机变量N服从二项分布B(n,p)。其概率分布律为

(2)计数的随机变量N服从参数为λ泊松分布。其概率分布律为

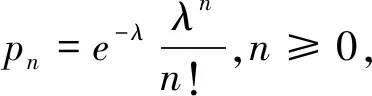
(3)计数的随机变量N服从参数为γ,β负二项分布。其概率分布律为

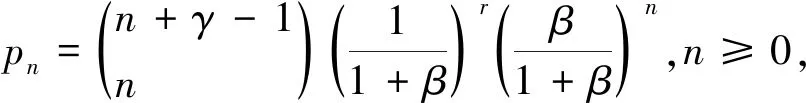
下面给出的三个数值例子，就是分别假设计数变量N服从二项分布、泊松分布、负二项分布。

例1(二项分布)：若X概率分布律如下，

X1 2 3

p1/2 1/3 1/6

此时f1=1/2,f2=1/3,f3=1/6。

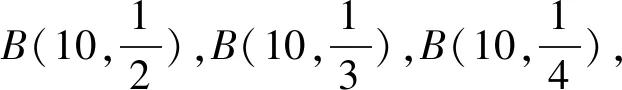
例2(泊松分布)：设N服从参数为λ的泊松分布，即a=0,b=λ。

假设X取值为正整数，若X概率分布律如下，

X1 2 3 4 5 6 7

p0.3 0.2 0 0.15 0.1 0.05 0.2

此时f1=0.3,f2=0.2,f3=0,f4=0.15,f5=0.1,f6=0.05,f7=0.2,

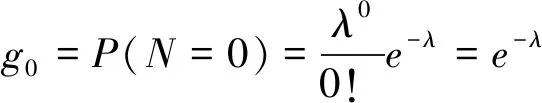
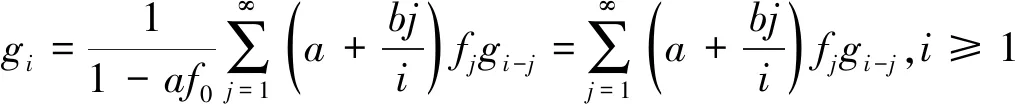
当N服从参数λ=1,2,3,4,5的Poisson分布时，我们计算出概率分布律gi,i=1,…,19如下:

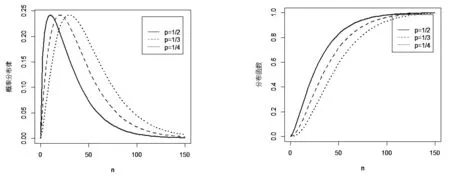
图1 随机和概率分布律 图2 随机和分布函数

表1 计数变量服从泊松分布时概率分布律

例3(负二项分布)：若概率分布律如下，

X1 2 3 4 5

p0.2 0.5 0.15 0.2 0.15

此时f1=0.2,f2=0.3,f3=0.15,f4=0.2,f5=0.15

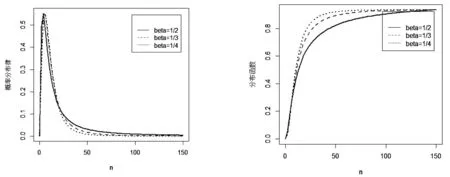
图3 随机和概率分布率 图4随机和分布函数

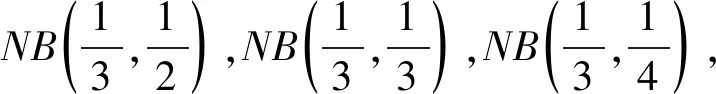
5. 总结

文中首先给出随机和的定义，证明随机和的概率分布律的递推公式，随后给出递推公式的算法，并给出几个数值的例子。相较采用全概率公式，文中给出的递推公式在计算概率分布律的效率和精度上有很大的提升，希望此方法在类似问题研究中能提供方法上的借鉴。