一种圆柱螺旋压缩弹簧多目标优化设计方法

张 慧 鹏

(运城学院 机电工程系，山西 运城 044000)

引言

圆柱螺旋压缩弹簧作为一种常用的弹性联接件，广泛地应用在工业生产、日常生活及各种机械设备中，其在工作中一般承受压缩力的作用[1]。在螺旋弹簧传统的设计方法中，首先根据要求的变形条件及最大工作载荷，参照已有的设计参数和经验，选择簧体材料，进而弹簧许用应力初步确定；其次在试选取弹簧旋绕比的基础上，利用弹簧设计公式计算弹簧丝直径，弹簧中径及工作圈数等基本参数；最后按照求得的三个基本参数，利用强度校核公式验算弹簧实验载荷和疲劳强度是否满足要求，若满足设计要求，则可继续计算出弹簧的其他几何参数，若不满足要求，则需重新进行设计[2]。因此传统的弹簧设计方法，需要工作人员具有一定的弹簧设计经验和较高的设计技能，一般无法获得最优设计方案，且设计效率低下[3]。相对于单目标优化设计，多目标优化设计可同时兼顾多项设计目标，能够得到更为均衡的设计参数，获得更为良好的整体性能，虽然比单目标优化问题复杂，但借助于MATLAB优化工具箱进行多目标优化问题分析，具有分析速度快，编程简单高效，计算结果准确等特点，从而有效缩短设计周期，提高设计质量。

本文分析了圆柱螺旋压缩弹簧设计目标、设计变量和约束条件，建立了基于弹簧结构质量最小、自由高度最小和自振频率最高的优化设计数学模型，采用MATLAB优化工具箱求解得到了优化的弹簧几何参数。这种方法极大减小了弹簧设计工作量，不需要人工反复迭代计算，同时实现弹簧轻量化和工作性能相对最优的目的。

1. 数学模型的建立

1.1 已知参数

内燃机用气门弹簧结构如图1所示，其工作性能指标为：工作载荷F=680N，工作行程h=16.59mm，工作频率fr=25Hz，寿命N≥106循环次数，弹簧丝直径2.5≤d≤9mm，弹簧外径30≤D≤60mm，工作圈数n≥3，支撑圈数n2=1.8，弹簧指数C≥6，弹簧压并高度λb=1.1h=18.25mm，弹簧丝材料采用50CrVA，许用切应力[τ]=405MPa。要求在满足弹簧的强度条件、刚度条件、稳定性条件、旋绕比条件和结构尺寸边界条件等约束条件下，使它的结构质量最小、弹簧自由高度最小和自振频率最高[4]。

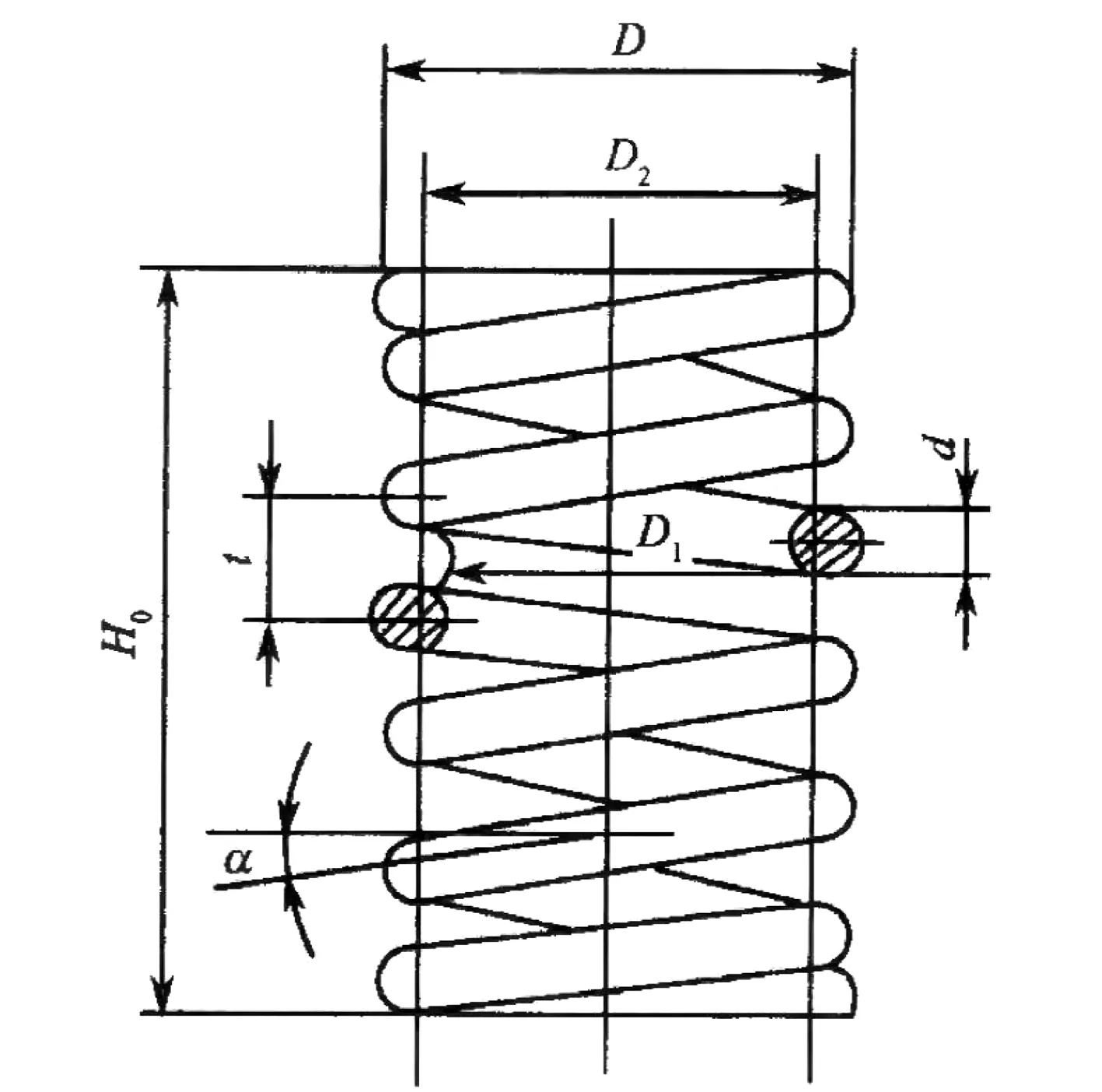
图1 圆柱螺旋弹簧结构简图

1.2 选取设计变量

在满足使用要求的前提下，选择质量较轻的弹簧，可使弹簧小型化，不受或少受布置空间的限制，且能节省材料，提高经济性，因此选择弹簧结构质量作为第一优化设计目标[5]，可表示为：

f1(x)=(n+n2)πD2ρπd2/4

(1)

式中，ρ—弹簧材料密度，ρ=7.8×103kg/m3。

弹簧自由高度是指弹簧不受外力时的高度，弹簧自由高度过大，容易使弹簧稳定性变差，故以弹簧自由高度最小作为第二优化设计目标[6]，可表示为：

f2(x)=(n+n2-0.5)d+λb

(2)

自振是弹簧本身的固有振动，弹簧的自振频率与弹簧的刚度、质量、承受载荷大小以及支承情况有关。当弹簧受到频率分量接近弹簧固有频率的外力作用时，容易出现共振现象，从而影响弹簧工作性能，故以弹簧自振频率最高作为第三优化设计目标[7]，可表示为：

(3)

比较优化设计目标函数中各设计参数之间的关系，可确定弹簧的簧丝直径d、中径D2和工作圈数n等三个独立设计参数作为优化设计变量，表示为：

(4)

1.3 确定目标函数

代入有关数据，并用设计变量表示弹簧结构质量表达式，则第一分目标函数可表示为：

(5)

用设计变量表示弹簧自由高度表达式，则第二分目标函数可表示为：

f2(x)=x1(x3+1.3)+18.25

(6)

用设计变量表示弹簧自振频率表达式，且因为优化设计算法搜索极小值，故第三分目标函数可取自振频率的负数表示为：

(7)

为了优化结果准确，应使三个分目标函数的极值在数量级上保持一致，因此应用目标规划法统一目标函数为：

(8)

2. 确定约束条件

对于弹簧来说，其约束条件除一般的尺寸约束、强度约束外，还应包括刚度约束、振动稳定性约束。其约束条件可根据弹簧功能的要求和结构限制列出，同时可根据其数学表达式的不同分类[8]：

2.1 线形不等式约束条件

(1)弹簧丝直径即制造弹簧的钢丝直径，制作弹簧的钢丝直径越粗，弹力越大，但抗拉强度极限反而下降，故要求弹簧丝直径2.5≤d≤9mm，即

g1(X)=2.5-x1≤0

gx(X)=9-x1≥0

(2)弹簧的有效圈数就是弹簧等节距的圈数，圈数越多，其弹性系数越小，刚度越小，而圈数过少，则易影响弹簧使用寿命，故要求弹簧圈数3≤n≤9，即

g3(X)=3-x3≤0
g4(X)=9-x3≥0

2.2 非线性不等式约束条件

(1)弹簧的弹性系数与弹簧的线径成反比，弹簧的外径越大，弹力越小，但小外径的弹簧稳定性差，故要求弹簧外径30≤D≤60mm，即

g5(X)=30-(x1+x2)≤0

g6(X)=60-(x1+x2)≥0

(2)弹簧指数又称旋绕比，用C=弹簧中径/弹簧丝直径表示，其影响弹簧的强度、刚度、稳定性及制造的难易。C值大，弹簧较软，刚性小，易变形，易绕制；C值小，则相反，弹簧较硬，刚性大，不易绕制。根据弹簧钢丝直径规格可选取4≤C≤9，即

g7(X)=4x1-x2≤0

g8(X)=9x1-x2≥0

(3)弹簧在工作时，弹簧丝横截面上的扭转切应力如果超过了强度极限，则弹簧可能在受力过程中断裂，故弹簧实际工作应力应小于许用应力，即簧丝的强度条件是：

(9)

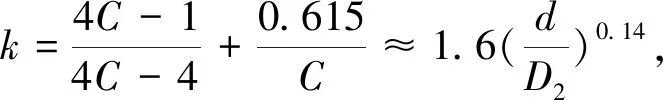
对上述公式代入有关数据，得约束函数：

(4)弹簧刚度是指载荷增量与变形增量之比，如果刚度不足，弹簧的工作行程将变大，工作性能受到影响，因此应满足刚度条件，即

(10)

式中，G—弹簧切变模量，G=82.6GPa；λ—弹簧工作时压缩变形量，λ=18.25/1.1=16.59mm。

对上述公式代入有关数据，得约束函数：

(5)压缩弹簧的长度较大时，受载后容易发生失稳现象，为了便于制造和避免失稳现象出现，一般推荐弹簧的长径比在两端固定时应≤5.3，即：

(11)

代入有关数据，可得约束函数：

(6)气门弹簧的作用是克服气门关闭过程中气门及传动件的惯性力，保证气门及时落座并紧紧贴合，为防止弹簧在运行中发生强烈颤振影响密闭性能，弹簧的自振频率通常至少应当是工作频率的10倍以上，即

(12)

可得约束函数：

经过分析，这是一个三维非线性优化设计问题，具有12个约束条件。

3. 利用MATLAB求解

3.1 编写目标子函数文件th_f.m

function f=th_mb(x)

f1=1.9236e-5*x(1)^2*x(2)*(x(3)+1.8);

f2=x(1)*(x(3)+1.3)+18.25;

f3=-3.56e5*x(1)/(x(2)^2*x(3));

f=((f1-0.0608)/0.0608)^2+((f2-40.3827)/40.3827)^2+((f3+1236.1)/(-1236.1))^2;

3.2 编写非线性不等式约束子函数文件th_ys.m

function[c,ceq]=th_ys(x)

c(1)=30-(x(1)+x(2));

c(2)=(x(1)+x(2))-60;

c(3)=4*x(1)-x(2);

c(4)=x(2)-9*x(1);

c(5)=x(2)^0.86/x(1)^2.86-0.1462;

c(6)=1-251.9118*x(1)^4/(x(2)^3*x(3));

c(7)=((x(3)+1.3)*x(1)+18.25)/x(2)-5.3;

c(8)=1-1424*x(1)/(x(2)^2*x(3));

ceq=[];

3.3 编写调用子函数的主函数文件th_z.m

x0=[2.5;21;3];

lb=[2.5;21;3];

ub=[9;57.5;9];

b=zeros(6,3);

b(1,1)=-1;b(2,1)=1;

b(3,2)=-1;b(4,2)=1;

b(5,3)=-1;b(6,3)=1;

c=[-2.5;9;-21;57.5;-3;9];

[x,fval]=fmincon(@th_mb,x0,b,c,[],[],lb,ub,@th_ys)

3.4 优化设计结果分析

各参数优化设计结果可见表1。由表1可以看出，弹簧质量优化和高度优化结果相同，这说明弹簧质量和高度优化目标一致，二者优化后参数无差异。多目标优化与质量和高度单目标优化相比，虽然弹簧结构质量增加8.55%，自由高度增加2.57%，但自振频率增加6.75%，能更好防止气门弹簧产生共振；与频率单目标优化相比，虽然自振频率减少14.60%，但质量相应减少17.29%，高度减少5.97%，经济效益相对更好。

因此，多目标优化相对于单目标优化，虽然在单个指标方面没有达到最优，但是各项指标更加均衡，弹簧综合性能更优，优化效果显著。

表1 各优化设计结果比较

4. 结论

在分析圆柱螺旋压缩气门弹簧尺寸约束、强度约束、刚度约束、振动稳定性约束的基础上，以结构质量、自由高度最小、自振频率最大为优化设计目标，采用Matlab优化函数对弹簧进行优化设计。优化结果表明，所建立的弹簧优化设计数学模型更符合弹簧设计要求，优化后的设计参数更为均衡，弹簧综合工作性能更好，因此弹簧多目标优化设计是一种行之有效的优化设计方法，且利用MATLAB有关函数进行优化设计，编程简单，算法可靠，结果准确，能够有效提高设计效率。