基于计算机仿真的缩孔缺陷对轮毂机械性能影响研究

张聚涛，王德祥

（1 唐山学院 河北 唐山 063000）

（2 王氏实业集团<唐山>有限公司 河北 唐山 063000）

0 引言

轮毂铸件是汽车的关键部件，必须能够长久地抵抗粗糙的路面和严酷的环境[1]。为了确保铝合金轮毂能够长期服役，考虑其服役中不同的疲劳特性，一些轮毂测试如冲击测试等早已开始应用。设计—测试—重新设计过程提高了轮毂设计的工作成本[2]。在现代工业中，计算机模拟分析是一个缩短研发周期的方法，以往研究中虽然运用计算机模拟研究轮毂机械性能的研究较多，但大多忽略了缩孔缺陷对轮毂机械性能的影响[3-4]。如图1所示，缩孔缺陷很容易在铸造过程中产生。缩孔缺陷对轮毂铸件的机械性能有很大影响，但当前对缩孔对轮毂铸件的定量作用的研究不够完善，对其缺陷及与机械性能的关系也未阐述清楚，导致在设计过程中，工程师经常不考虑轮毂铸件的缩孔缺陷。这并不能满足如今的铸造轻量化需求，因此有必要寻找一个研究缩孔缺陷影响的方法。本研究建立了缩孔缺陷对铸件机械性能的影响关系，分析了缩孔缺陷对轮毂冲击测试的作用。

图1 缩孔缺陷示意图

1 缩孔模型

本文采用三个建模方法对于缩孔的建模与结构进行分析。直接塑造法（DSM）、材料性能还原法（MPRM）和形貌简化法（SSM）。DSM直接从铸件缩孔原始形貌中生成有限元网格[5]。MPRM的理论为：假设孔隙之间没有相互作用，材料弹性模量在最低的孔隙率范围，能够通过线性关系进行描述。SSM模型建模缩孔对空心球体作用，它是最小的球体装入缩孔的STL格式，且反映出缩孔的应力集中作用，因此，本文采用SSM研究轮毂缩孔缺陷的机械性能。

2 数值模拟

2.1 动态应变集中系数

应变集中系数广泛应用于评估应变梯度在一个对象中的作用。为了冲击模拟，本文引入动态应变集中系数DSCF。动态应变集中系数定义如下：

其中ε是一个时间t的函数，εmax和εnom分别为最大应变和名义应变。在一个对象具有如图2所示球体缩孔的情况下且在静态载荷下，分析值K（t）可以评估为2.05。通过图2中的参考数据以及按照D.R.Weaver’s[5]的结论，本文采用2.05作为分析值，研究结果的收敛取决于单元类型和尺寸。

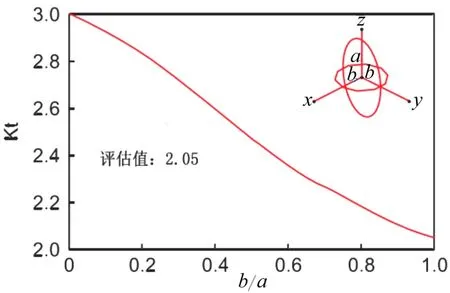
图2 应力集中系数

2.2 单元类型选择和单元尺寸确定

为了研究冲击模拟的收敛和准确性，基准分析使用了具有球体缩孔在中心的矩形条，图3给出了棒的对称半模型和数值模拟条件。冲击模拟结果对单元类型和尺寸非常敏感。为了确保准确性，在冲击模拟中实体单元通常优先于四面体单元，但它在真实的具有复杂形貌的铸件产品中难以产生网格[6-7]。由于四面体单元更具有普遍适用性，因此在本研究中采用四面体单元。试验中选取三个冲击模拟试验，元素尺寸从模拟1到模拟3在缩孔表面越来越细。单元尺寸定义为简化缩孔的半径r。从模拟1到模拟3，如图4所示。随着网格逐渐细化，通过FEM获得的DSCF逐渐收敛于分析解，计算成本恰好收敛于2.05。细的网格不仅仅应用在缩孔的表面还应用于缩孔周围。考虑到网格的工作效率，对于在缩孔表面本文推荐一阶四面体单元尺寸为0.125。

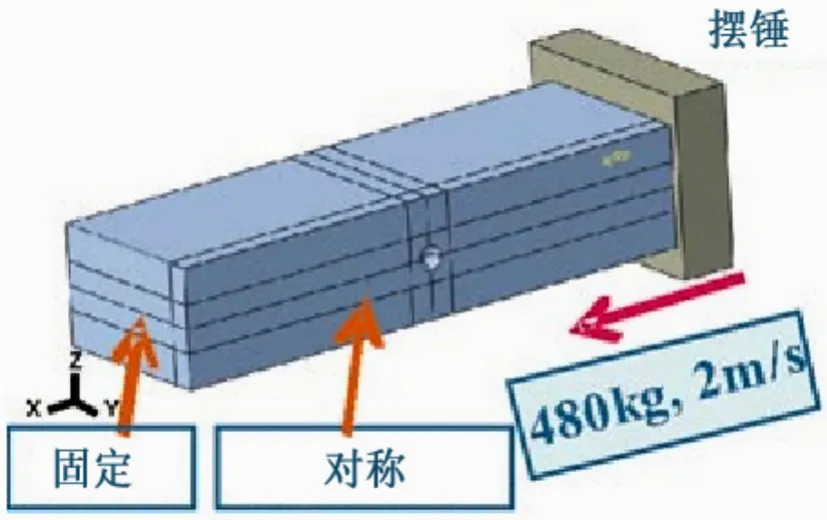
图3 简单的棒状纤维模型

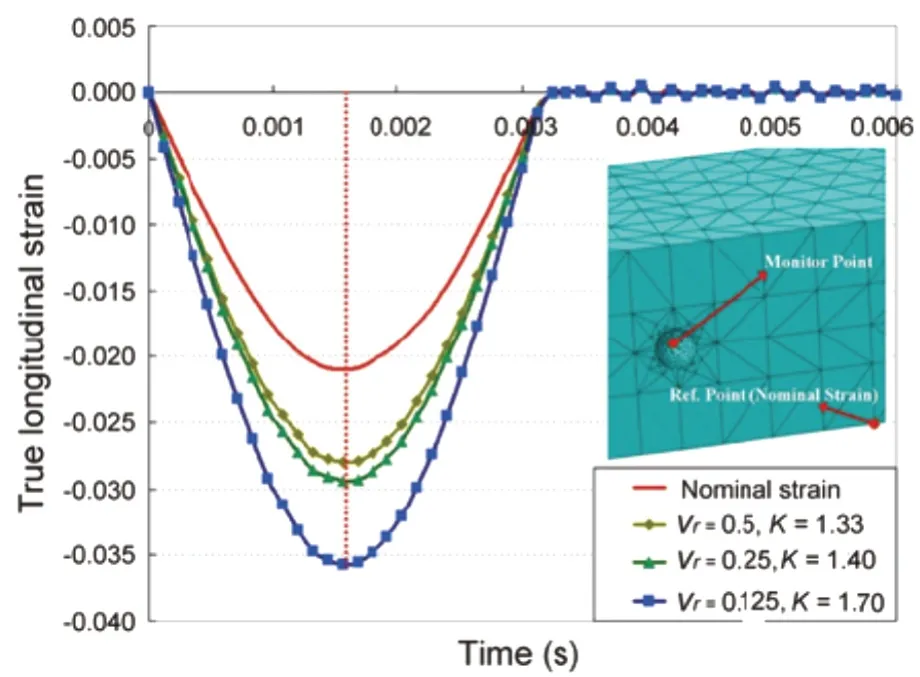
图4 元素尺寸与真应变关系

3 计算机仿真测试

3.1 轮毂冲击测试

图5所示为轮毂冲击测试机器。它包含480 kg摆锤，接触表面尺寸为375 mm×125 mm。轮毂安装在与水平面倾斜13°角上，所以它的最高点垂直于冲击作用前锋，摆锤下落高度为230 mm，这高于轮辋凸缘的最高部分。在本研究中，冲击模拟对于轮毂依据SAE J175-Wheels-Impact Test Procedures-Road Vehicles。模型和设置在冲击模拟中如图6所示，分析包括两个情况：考虑缩孔缺陷和不考虑缩孔缺陷。

图5 冲击载荷控制机器

3.2 建模和条件

图6所示为轮毂和摆锤的模型。摆锤的质量是

图6 模拟的模型设置

其中W是最大静态轮毂负载轮毂或者汽车制造者指定，单位为kg。摆锤初始速率：

其中g是重力加速度，h是摆锤下落高度。

图7为试验机冲击过程中利用光电编码器每隔8 ms所采集的冲锤位移数据，通过PLC传输后得出速度、时间之间的关系图。冲击过程中实际速度与V0有所偏差，约为2.074 m/s。这主要是由于形体轮与导轨间所具有的摩擦阻力以及电磁化后的锤体与电磁体之间的相互作用力所导致的，另外末端速度的测量过程中也存在误差。

图7 速度—时间曲线

图8描述了从工业CT获得缩孔数据和建模具有简化形貌的缺陷的过程。这个工作主要过程包括两步：第一步是通过CT获得立体像素信息，第二步是还原成STL。

图8 通过CT获取和建模收缩数据

因为STL文件是极其细小的，所以它不易从STL文件产生网格直接获得自工业CT且不使用任何修正网格生成的工具。因此，原始的CT-TSL格式模型应该加工成满足产生网格的需求。为了做到这一点，本研究使用了一个特定的ImageWareTM程序。最终通过CAD格式，缩孔模型简化为椭圆体模型。

如图8所示，一个是（缩孔A）接近于轮辐和轮辋的相互作用区，另一个是（缩孔B）接近于轮辐和轮毂的相互作用区。

4 结果与讨论

模拟结果表明，最大应变发生在0.000 87 s即摆锤接触到轮毂后。这是轮毂冲击试验的临界时间点，所有接下来的结果都集中于这个时间点[8-9]。轮毂变形或断裂在于摆锤前锋相接触的轮辋断面在SAE J175中不构成失效，所以本文只对摆锤接触面以外的区域进行了研究。如图9所示，无缩孔缺陷的条件下，轮毂被认为能够通过冲击测试。图10所示为在有缩孔缺陷条件下的等效塑性应变等高线。对于缩孔缺陷A，最大主弹性应变在孔表面小于0.001 m处且没有塑性变形发生。然而对于缩孔B，最大等效塑性应变（0.077）出现于孔表面超过了0.059 m处，所以轮毂被认为可能从缩孔B断裂。在真实的测试依靠计算分析很难预计是否会发生断裂，如果将缩孔缺陷考虑进去，就能够大大提高轮毂机械可靠性。工程师在工作过程中可以通过考虑缩孔的生成从而对轮毂工艺制定起到指导作用。

图9 等效塑性应变图（无缩孔影响）

图10 等效塑性应变图（缩孔影响）

5 结论

综上所述，本文研究了缩孔缺陷对于铸件承受实际冲击载荷表现的作用。文中提出了在铸件中考虑缩孔缺陷冲击模拟的技术方法，通过使用工业CT扫描缩孔缺陷的方法以及SSM建模的手段。并且对铸铝轮毂冲击测试进行了分析，结果表明：缩孔位于高应变区域比在低应变区域可能更加有害。本文提出的方法可以反映应变集中作用和改善模拟精确度。