基于特征聚类优化的KM-FCM-RF算法研究

罗 超，彭玉涛

（井冈山大学网络信息中心 江西 吉安 343009）

0 引言

在常用的决策树算法中，最常见的算法是随机森林算法。随机森林算法的优点在于通过对数据噪声的高度容忍度来得到较高预测精确度。Chai[1]将随机森林算法运用到化工故障分类，提高了故障检测精度；Cheng[2]在网络安全方面运用随机森林算法，极大提升了网络安全监测正确率；Zafari[3]在化工项目评估管理领域运用随机森林算法，得到了更加准确的评估预测结果。

在具有明显优点的同时，随机森林算法也存在一些缺点，例如对数据集的特点相近似聚类的检索效率比较低，对数据集的动态聚类数据泛化特征时造成的误差估值往往比较大。针对这些缺陷，也有很多学者做了大量的研究以改进。王德军等[4]、刘曙光等[5]、王磊[6]分别采用时间序列特征泛化聚类、遥感数据多时相动态聚类、加权平均泛化数据后聚类的方法，得到了对精度不同程度的提高，并且聚类的效率也得到了相应的改善。对随机森林算法提出了非常有用的改进和补充。

本文将尝试采用将特征聚类KM算法与FCM算法相结合，对随机森林算法进行优化，形成KM-FCM-RF算法优化模型。对多模动态K均值聚类和模糊C均值互相融合与补充的方法，采用对多模动态数据集的特征数据进行聚类，对传统的随机森林算法进行优化后，再计算特征优化的差异化DBI的值，重新对DBI序列值进行排序，筛选相关的特征，在聚类多模动态数据时达到提高效率的目的。

1 传统随机森林算法

如果研究人员用Ntree表示决策树中多维特征的数量，OOBi表示第i棵决策树的多模动态数据的特征数据，ErrOOBi代表的是OOBi中错误数据样本的数量，如果有一个数据集的特征有d个，那么这个数据集可以称之为数据集D，XJ（j=1,2，…，d）表示该数据特征集的度量，其算法步骤如下：

步骤1：首先基础得到多雾的样本数量ErrOOBi的值；

步骤2：置换后，得到了XJ，

再次置换后得到；

步骤3：均值计算得到的值，可以表示为

步骤4：重复以上步骤1到步骤3，执行次数限定为Ntree次，循环结束后可以得到{ErrOOBi，i=1,2，L，Ntree}

步骤5：根据以上两个输出结果，可计算粗聚类变化的均值：

则可以认为多模动态数据集的聚类集合就是VI（XJ）。

通过步骤1到步骤5，可以看到随着多模特征集中特征维度的增加，循环训练需要更多的时间，结果就必然减缓了训练速度，进而降低多模数据特征集的训练效果。本文拟采用高维多模聚类的方法，对以上的算法进行优化改进，已加快训练速度和提高性能。

2 基于多模高维聚类优化的方法

2.1 聚类方法介绍

将K均值聚类（KM聚类）和模糊C均值聚类结合后，划分多模动态特征族，排序后进行聚类。优化后得到训练误差均值DBI，DBI中最小值的聚类特征则为最终的结果，也是最佳结果。

2.1.1K均值聚类

根据春花等[7]的研究，K均值算法中，多模数据集中数据特征样本的距离与相似度是反比关系。已知出事聚类和聚类中心，分别用K和C表示，则（C=｛μi，1≤i≤K｝）。

迭代计算的步骤为：

步骤1：得到每一个多维动态特征样本的中心聚类值；

步骤2：重新聚类分簇，并计算DBI。

重复执行步骤1和步骤2,

步骤3：计算误差平方和（SSE），一直到符合收敛条件。（SSE）的计算公式为：

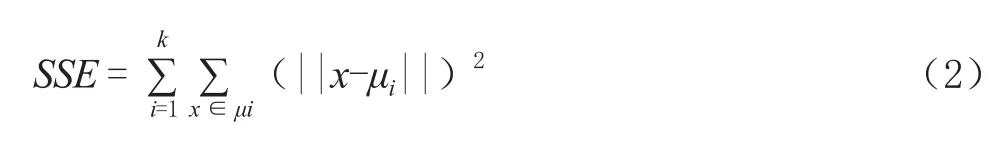
2.1.2 模糊C均值算法（FCM）

模糊C均值算法主要计算数据集中样本与聚类中心的关联隶属度，来完成对多维特征数据分类[8]。存在多维动态数据集Dn×p，其中的样本数量为n，隶属度矩阵U的计算公式为：

再计算每个样本集聚类中心V，计算公式为：

则J（U,V）可以用下式表示：

||xi-vj||表示样本各个聚类中心的均值。

2.1.3 离散相关度计算

使用KM和FCM算法对动态多模数据集的特征计算中心差异聚类时，计算出DBI的值，用来表示离散相关度索引的值。利用以下的公式来计算聚类中心最佳值：

（1）均值离散相关隶属度：

（2）各聚类中心的距离值：

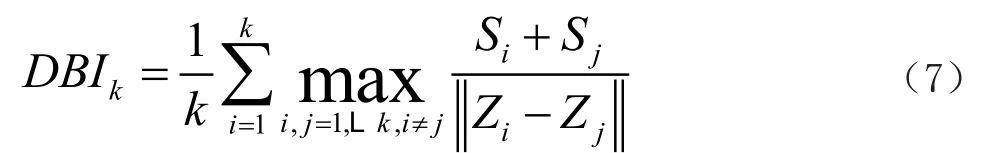
根据朴尚哲等[9]的研究，此时DBI的值为最佳聚类中心的值。

2.2 HDC-RF算法

2.2.1 KM-FCM-RF特征评估算法

对多维数据集进行聚类，并且根据聚类中心值的均值误差来进行排序。

步骤1：采用传统随机森林算法，计算出样本数据多维特征，并以此为排序的根据。

根据Alon[10]的研究，使用皮尔逊相关性系数ρxy来衡量族内特征与分类信息的相关性。

在上式中，特征x的均值用Zx来表示，特征y的均值则用Zy来表示，

ρxy表示皮尔逊相关系数，系数越大，则表示数据集特征之间具有越大的相关程度。

步骤2：根据阈值δ，筛选出相关系数ρxy＞δ的高维特征。本文改进的阈值δ计算公式表示为：

根据式（9）计算出多维动态数据集特征，采用排序的规则为簇内优先、簇间其次。最终，计算得出了多维动态数据集的特征簇序列。

2.2.2K均值和C均值优化的随机森林算法流程

在以上算法的基础上，将K均值C均值优化的随机森林算法优化流程用下图1表示。

图1 算法流程图

3 实验分析

3.1 实验准备

采用Alon等[10]和Golub等[11]提供的高维多模动态特征数据集作为输入的样本数据集。输入之前，先将数据和特征清除冗余，最终数据表征如下表1所示：

表1 实验数据集

根据表1的结果可以看出，多个高维特征数据集差别不大时，KddCup99由于具有更小的特征数，可以更方便地对数据集中的少量非高位数据集进行特征提取，并进行输出对比。反之，Minst则由于具有更多的特征数和更高维度，更适用于高维数据集的特征提取和对比。

在进行仿真实验时，决策树采用的是具有200个决策树的C4.5基本分类器，并将其最佳聚类范围设置为实验结果的预测阈值评价采用ACC标准。如果阈值越大，则算法的优化效果越好、聚类数据集的性能就越高。

3.2 实验结果

将本文的优化算法与传统的随机森林算法分别运行在KddCup99和Minst数据集进行比较，为了得到更稳定的结果，将算法运行30次的均值作为最终结果。实验结果对比如下图2、图3所示：

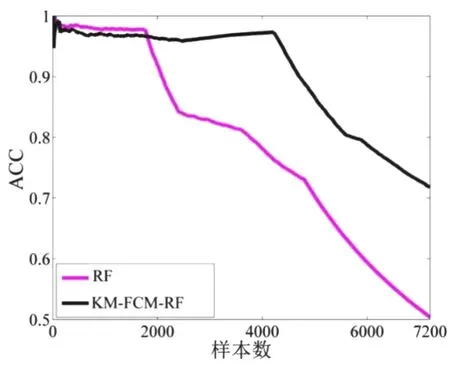
图2 KddCup99中KM-FCM-RF、RF预测精度对比

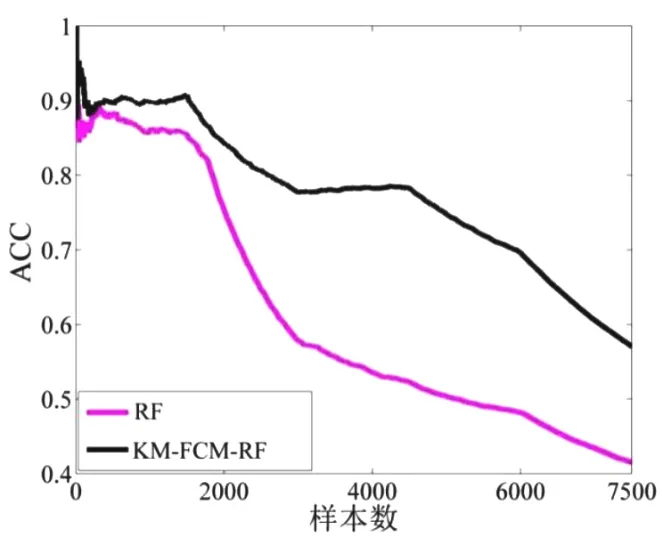
图3 Minst中KM-FCM-RF、RF预测精度对比

根据以上两图可以得到如下结论：

（1）根据图2的结果可知，在KddCup99的中低维数据集训练中，KM-FCM-RF算法在前200个样本时，预测精度略比RF略小，但从2 000个样本开始，预测精度一直高于传统RF算法。

（2）图3表明，在Minst的高维数据集上的训练过程中，KM-FCM-RF的精度自始至终都比传统RF算法高。

4 结论

针对传统的随机森林算法在多维特征数据集预测精度不高，本文提出了一种基于K均值和C均值优化聚类的随机森林算法，即在对多维特征数据集样本聚类后，集合K均值模糊C－均值算法结合，计算得到DBI指标并对该指标排序后，进一步得到的阈值δ比较，最终得到多维特征数据集的特征序列。实验结果表明，经过本文优化后基于K均值和C均值优化聚类的随机森林算法，具有更好的聚类效果、预测精度更高，具备良好的可行性。